Markov 链与Q-Learning算法的超轻度混动汽车模型预测控制

尹燕莉，马永娟，周亚伟，王瑞鑫，詹 森，马什鹏，黄学江，张鑫新

（1.重庆交通大学 机电与车辆工程学院，重庆400074，中国；2.包头北奔重型汽车有限公司，包头014000，中国）

随着环境与节能问题的日益突出，混合动力汽车（hybrid electric vehicle，HEV）因其独特的结构能达到节能、低排放的特点，成为当今最具有实际开发意义的新能源汽车[1-2]。能量管理控制策略是决定混合动力汽车燃油经济性和排放的关键技术，其主要包括基于规则[3-7]及基于优化（瞬时优化、全局优化）的策略。其中，基于规则的控制策略简单，容易实现，但未考虑工况的动态变化。瞬时优化控制策略[8-10]执行效率高，能够保证在每一个步长内是最优，但无法确保在整个行驶工况内的最优。全局优化控制策略能够保证整个行驶工况内整车性能的最优[11-14]，但行驶工况必须提前获知，且该算法程序复杂，运算量大，无法单独实现车辆的实时控制。

为了更好地实现混合动力汽车的能量管理，近年来国内外一些学者利用模型预测控制（model predictive control, MPC）的先进性，基于其基本原理预测车辆在未来时间域内的行驶状态，并根据预测信息优化混合动力汽车转矩分配。该控制策略既能克服瞬时优化控制策略不能实现全局最优的弊端，又能解决全局优化控制策略程序复杂、计算量大的问题。

目前针对MPC能量管理策略，国内外学者根据其基本原理从预测模型、求解方式两个不同实现要素方面对其进行深入研究。

基于不同预测模型的MPC能量管理策略主要是指采用不同的模型来预测未来的工况信息。有学者将未来预测时域内的工况信息描述为呈指数变化形式，然后优化求解实现功率分配[12,15]。该预测方式简单，易于实现，但其基于固定的数学模型，将实际工况的变化过于理论化，无法准确预测车辆的动力需求。基于此，赵韩等[16]提出利用Markov模型预测车辆需求转矩的方法。在此基础上，钱立军等[17]将加速度的变化视为一个具有Markov性质的随机过程，考虑到实际工况的不确定性，使预测准确性得到改善。SUN用神经网络对车速进行预测，实现能量优化分配[18-19]。上述预测方式均基于标准循环工况或本车历史工况数据，一旦更换整车工况信息，适应性就变差，预测结果准确性变差。近几年随着智能交通系统及车联网技术的发展，预测信息的获取也越来越多元化[20-22]，预测结果也越准确。

根据预测模型获取的未来工况信息，结合不同算法对其进行滚动优化求解。动态规划算法（dynamic programming, DP）采用多阶段决策来进行寻优，能够获得全局最优的优化结果，大多数学者采用DP对预测信息进行优化求解[23-24]，但该求解方式计算复杂，存在计算量大，运行时间长等问题。秦大同等利用二次规划（quadratic programming , QP）算法进行求解来改善计算量大的问题[25-26]，但QP不适合求解大规模的非线性问题，且稳定性有待提高。也有学者利用其他优化算法如广义最小残差方法[27-28]、庞特里亚金极小值原理[29-30]等对动力源需求转矩进行求解，能够保证实时性，但算法本身也存在一定的局限性。本文采用的Q-Learning算法来实现优化求解，它是一种有效的智能算法，优化求解时既能提高计算效率又能获得局部最优解，近年来被逐渐应用于混合动力汽车，用来解决能量管理的问题[31-34]。

本文以一款超轻度混合动力汽车为研究对象，提出一种基于Markov链与Q-Learning算法的模型预测控制策略。通过建立多步Markov模型预测未来的加速度变化过程，计算得到未来的需求功率；采用Q-Learning算法对需求功率进行优化求解，将离线优化和在线应用很好地结合，通过不断地与环境产生互动获得即时回报以探索获得最低燃油消耗时所对应的最优转矩分配序列；将该最优序列的第1个控制量施加给车辆，实现反馈优化。

1 超轻度混合动力汽车模型

1.1 整车结构与组成

本文以一款并联结构的超轻度混合动力汽车为研究对象，其主要由发动机、电动机、电池、回流式无级变速器等主要部件构成。电池组连接电动机输出电能转矩，离合器将发动机与电动机相连接，实现转矩耦合。该车使用回流式无级变速器作为传动机构，具有速比变化范围大、传动效率高以及低转速高承载能力的特点。发动机和电池可以单独驱动车辆行驶，制动时，电动机又可用作发电机回收制动能量为电池充电。结构简图如图1所示，整车主要参数如表1所示：

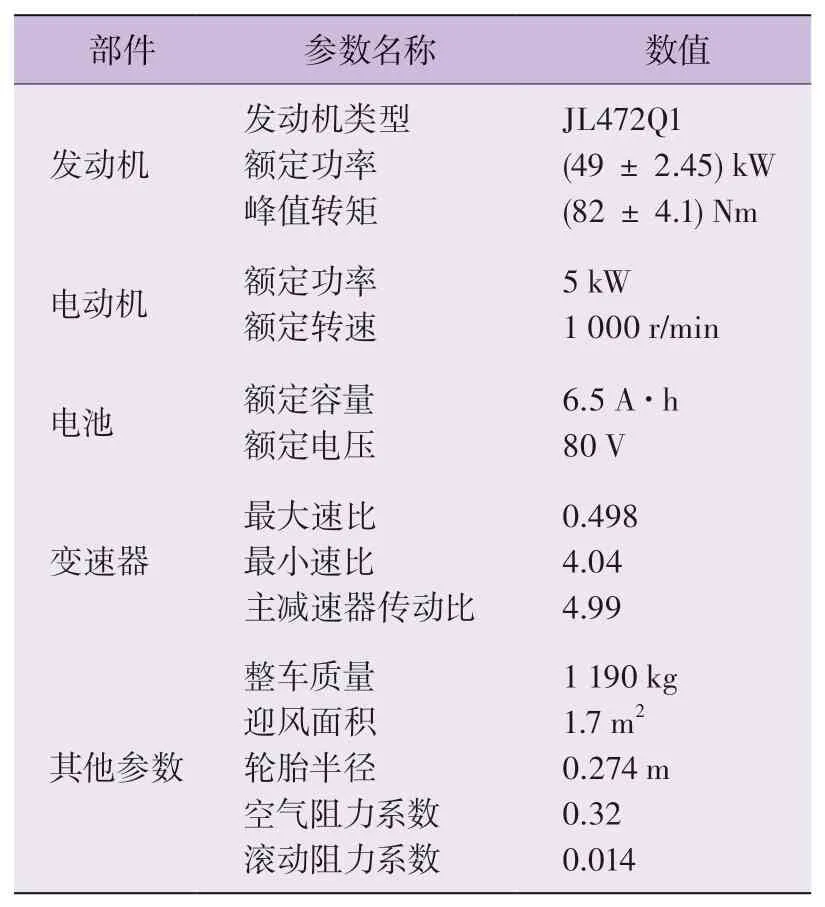
表1 整车主要参数

1.2 需求功率模型

混合动力汽车在行驶过程中克服阻力所需要的功率,即需求功率，由滚动阻力、空气阻力以及加速阻力产生的功率组成，这里忽略坡度阻力。车辆在任意工况下的整车需求功率如式（1）所示：

其中：Preq为车辆行驶需求功率；m为整车质量；g为重力加速度；f，CD，δ分别代表车辆的轮胎滚动阻力系数、空气阻力系数、旋转质量换算系数；A为迎风面积；v为车速；dv/dt为车辆加速度。

1.3 发动机模型

发动机是混合动力汽车的主要动力源，其转矩分配以及耗油量对整车燃油经济性有着重要的影响。通过试验获得不同转速、节气门开度下的发动机转矩数据，建立以发动机转速和节气门开度为输入、转矩为输出的数学模型，如图2所示。

1.4 电动机模型

超轻度混合动力汽车的电动机既可以单独驱动车辆，也可以在制动时作为发电机回收制动能量给电池充电。电机功率可以表示为：

其中：Pm为电动机功率；Tm为电动机转矩；nm为电动机转速；ηm为电动机效率，是电动机转矩和转速的函数。通过对电动机及其控制系统进行性能测试，得到电动机的实验数据，然后拟合实验数据，可得到电动机转矩与转速的关系如图3所示。

1.5 电池模型

电池组作为超轻度混合动力汽车的另一个动力来源，其主要功用相当于“蓄水池”。在驱动工况时释放电能驱动车辆行驶；在制动时回收制动能量存储电能，本文要求电池能量在整个行驶工况中要保持平衡。不考虑温度变化和电池寿命的影响，建立电池的电动势和内阻模型。

其中：Esoc表示当前状态下的电动势，E0表示电池电动常数拟合系数，SOC是电池的荷电状态。

其中，Rsoc表示当前状态下的内阻；δ0表示内阻随电流变化的补偿系数；R0表示电池的内阻常数；λi表示拟合系数。

电池的SOC是剩余电量与电池容量的比值，其值随着车辆运行状态的改变而改变。电池SOC的计算公式如下：

其中：I表示电池的电流；Qbat表示电池容量；Pbat表示电池功率。

2 基于Markov链与Q-Learning算法的模型预测控制（MPC）

从数学与控制理论的层面来看，混合动力汽车的能量管理策略问题可以归属于一个受限制性条件约束的非线性动态最优化控制问题。MPC将复杂的优化问题划分为有限预测时域内的数学规划问题并分区域求解，提高计算效率的同时还能获得局部最优解。

MPC的控制原理为在每一个采样时刻，都遵循3个步骤：预测系统未来动态—求解优化问题—解的第1个元素作用于系统[35]，在下一个时刻，将测量的实际输出值与参考值作比较后修正预测模型，重新进行求解，重复进行上述步骤滚动求解优化问题，直到预测时域结束。滚动优化，就是在每一时刻，优化过程是从该时刻到预测时域的范围内，在下一时刻时，优化范围会同时向前滚动一个采样时段，每一时刻的控制量也随优化时段向前更新。

本文将Markov链与Q-Learning算法相结合构建了超轻度混合动力汽车模型预测控制模型，其主要包括3个部分，如图4所示。

1） 预测模型。基于ECE_EUDC+UDDS标准循环工况数据，采用Markov链方法，获取加速度转移概率矩阵模型，从而预测出下一时刻的加速度。同时，在每一时刻，将当前时刻的实际工况数据作为预测模型的输入对未来的工况数据进行预测。

2） 滚动优化。在预测时域内，建立以燃油经济性为目标的整车优化模型，根据获取的未来工况数据，采用Q-Learning算法求解该时域内的转矩优化问题。即在k时刻获得预测区间[k，k+p]内的最优控制序列[Tm(k),Tm(k+ 1|k),Tm(k+ 2|k),…]，然后在k+ 1时刻获得预测区间[k+ 1，k+p+ 1]内的最优控制序列[Tm(k+ 1),Tm(k+ 2|k+ 1),Tm(k+ 3|k+ 1),…]，依此类推，即为滚动优化过程。

3） 反馈校正。获得预测时域的优化控制序列后，仅将预测时域第一个控制量Tm(k)施加给车辆，从而产生控制输出量。在下一个采样k+ 1时刻，以车辆实际测量输出值v(k+ 1) 、a(k+ 1)作为反馈信息，重新预测系统未来输出并求解优化问题。通过闭环反馈校正，不断修正系统的预测值，可减小系统不确定性对控制性能的影响，从而提高系统的控制精度和鲁棒性。

2.1 基于马尔可夫链的预测模型

2.1.1 Markov链理论

在一个控制系统中，给定当前状态信息的情况下，过去的信息（即当时以前的历史状态）对于预测将来的信息（即当时以后的未来状态）是无关的，把这种无关性质称为Markov性，把用来描述具有Markov性质离散时间的状态与状态之间的转移过程，称为Markov链。即在某个起始状态下，按照状态转移概率得到的可能的状态序列。

在车辆的实际行驶过程中，汽车的加速度能够准确地描述行驶过程中的加速、减速等驾驶行为，且未来某一时刻的加速度变化与历史状态信息无关，只与当前时刻的加速度变化信息相关，具有Markov性，因此本文选取加速度作为状态量对未来的驾驶信息进行预测。

2.1.2 基于Markov链的加速度转移概率矩阵模型

Markov预测模型可分为单步预测模型及多步预测模型。单步预测模型即在统计加速度变化信息时只记录每个当前时刻到下一时刻的加速度转移概率，对应于每个当前时刻只能得到一个转移概率矩阵；多步预测模型是需要记录每个当前时刻到未来任一时刻的加速度转移概率，对应于每个当前时刻有多个转移概率矩阵。采用单步预测，会造成预测误差的累积，且由于预测步长较小，加速度变化较相差不大，会使得预测加速度与实际行驶过程中的加速度偏差较大，影响预测时域内的优化结果。而多步预测加速度发生转移的概率比较分散，更能准确地模拟实际驾驶行为，能够减小预测误差，获得比较准确的加速度预测结果。综合以上分析，本文选取多步Markov预测模型。具体步骤如下：

将ECE_EUDC与UDDS工况结合作为样本工况来提取车速及加速度数据。采样步长取1 s，工况最高车速为120 km/h，车速离散间隔为5 km/h；工况最大加速度为1.5 m/s2，工况最小加速度为-1.5 m/s2，加速度离散间隔为0.1 m/s2。将车速及加速度按离散间隔离散成式（8）的形式。

假设当前时刻为k，记录在每一时刻，当前时刻车速及加速度到预测时域p（p= 1,2,3,…,p）内任意时刻的车速及加速度变化信息，即可获得每一离散的车速z下，加速度由当前时刻的状态i转移到下一时刻状态j的次数Si，j，由式（9）计算得到该车速下加速度由i转移的总次数Si。

利用最大似然估计法（式10）计算获得每一离散车速下加速度的转移概率。每一个离散车速值下都会对应p个加速度转移概率矩阵，这些转移概率矩阵即所建立的多步Markov预测模型，对相应时长的加速度进行预测。

其中，Pz,i,j为当前离散车速z下，加速度由i转移到j的概率。

通过以上步骤，计算出车速为35 km/h时加速度的多步转移概率矩阵模型，如图5所示，由图5可以看出，当预测步长较小时，加速度转移概率较为集中，呈对角线分布；随着预测步长的增加，加速度的转移概率由分布集中转变为分散趋势，且步长越长，这种趋势越明显。这是因为预测步长较小时，加速度变化相差不大，而随着步长的增加，加速度变化的情况就越随机，进行转移的可能性就越多，加速度转移概率就越分散。

2.1.3 基于Markov链的车速预测模型

基于上述建立的多步Markov预测模型，结合当前时刻k的车速v(k)及加速度a(k)作为转移概率矩阵的输入，选取概率最大的加速度值作为下一时刻k+1的实际加速度值a(k+ 1)，由式（11）计算得到下一时刻的车速值v(k+ 1)。在k+ 1时刻及未来有限时刻重复此过程即可获得预测时域内的全部车速及加速度信息。

下一时刻车速计算如式（11）所示

利用建立的多步Markov模型，在不同预测时域下分别对车速进行预测，选用均方根误差对预测结果进行评价，其计算方法如式（12）所述。

其中：R(k)为k时刻预测时域内的均方根误差，v(k+ i)为k时刻循环工况的实际车速，vnp(k+ i)为k时刻预测得到的车速，np为预测时域，Re为整个循环工况内总的均方根误差，L为循环工况的总时长。Re的值越小，说明预测车速与实际车速之间的差距越小，预测结果越准确。

车速为35 km/h时，基于多步Markov预测模型在不同预测时长下进行预测，预测结果的均方根误差见表2，预测效果图见图6。

表2 多步Markov不同预测时域的均方根误差

从图6可以看出，在预测步长较小时，预测车速与实际车速变化轨迹几乎重合，这说明预测车速能够很好地追随工况车速，预测误差较小；预测时域越长时，预测车速与实际车速变化轨迹偏差增大。表2中不同预测时域下的Re值也验证了这一预测情况。这是由于在实际行驶过程中，车速变化受到驾驶员驾驶习惯及周围驾驶环境等诸多因素的影响，车速变化过程随机性很强，难免存在预测误差；再者，采用Markov模型对车速及加速度进行预测，会存在误差的累积。

2.2 基于Q-Learning算法的滚动优化模型

2.2.1 滚动优化模型

基于Markov链加速度预测模型获取预测时域内的加速度信息之后，需要优化求解获得该时域内的最优控制序列，保证局部控制性能最优。该优化过程是特定时域内的滚动优化，是反复在线进行的。即在每一个采样时刻，结合目标函数求解该时刻及预测时域内的最优指标值，在下一采样时刻，优化范围向前推动。滚动优化示意图如图7所示，在当前k时刻，假设预测时域为p，求出预测范围k～k+p内的最优控制序列[u(k)，u(k+ 1 /k)，u(k+ 2 /k)，…，u(k+p/k)]；在k+ 1时刻，采用相同的方法求出新的预测范围k+ 1～k+p+1内的最优控制序列[u(k+ 1)，u(k+ 2 /k+ 1)，…，u(k+p+ 1 /k+ 1)]，以此类推，直到预测时域结束，即为滚动优化过程。

目前，采用模型预测控制解决能量管理问题时大都使用动态规划算法（DP）来实施优化求解。DP采用逆向搜索，正向寻优的迭代搜索方式，求解多阶段决策问题，来获得预测时域内的全局最优解。但DP求解时计算量大，运行速度较慢，难以实现实时控制，且不适用于求解具有多个状态量的优化问题。因此，本文采用Q-Learning算法实施优化求解。

Q学习算法是强化学习方法中一种由数据驱动的表格型智能算法，由于它基于数据不断地进行“试错”学习来寻优，相较于动态规划算法的多阶段决策的寻优过程，可以有效减小计算复杂度，提高计算效率，在处理复杂的多状态量系统优化时有明显的优势。

2.2.2 Q-Learning算法概述

Q-Learning算法由有限状态集S、有限动作集A、状态的概率转移矩阵P、回报函数r和折扣因子γ五要素组成。该算法以控制系统为智能体，除控制系统外为环境，控制变量为动作。该算法针对状态-动作值函数Q(s, a)进行迭代更新，智能体需要不断探索环境来寻找最优Q(s, a)值所对应的动作策略。

Q-Learning算法的原理为：在当前k时刻，智能体从环境中获取当前时刻的状态s，利用ε-greedy策略选择合适的动作a作用于环境，获得当前状态-动作对的立即回报r，同时产生k+ 1时刻状态st+ 1，并评估回报以此来更新状态-动作值函数Q(s, a)值。智能体探索环境的过程也称为学习的过程，经过不断的迭代学习，直至Q(s, a)表收敛，利用贪婪策略（greedy策略），选择每一状态对应最大奖励的动作，最终获得所有状态的最优控制策略。

2.2.3 Q-Learning求解优化控制问题

超轻度混合动力汽车的优化问题求解就是解决车辆的转矩分配问题。根据预测获得的加速度结合式（1）求出预测时域内的需求功率，采用Q学习算法进行优化求解。首先，计算出预测时域内每一离散车速下的需求功率转移概率矩阵；其次，选取预测时域内电池荷电状态SOC、需求功率Preq为状态变量，电动机转矩Tm为控制（动作）变量，以整车燃油消耗量最小为优化目标，建立优化模型，获得预测时域内燃油消耗量最小所对应的最优转矩分配序列。

根据Q-Learning算法原理，按以下步骤来求解预测时域内的车辆转矩分配问题。

1） 选取预测时域内电池荷电状态SOC、需求功率Preq为状态变量，电动机转矩Tm为动作变量。

2） 确定目标函数和约束条件

通过等效因子将电池能量变化等效为燃油消耗，构建以整车等效燃油消耗量最小为目标的回报函数，将最小累积回报的期望作为目标函数。

其中：k～k+np为预测时域，Jk为预测时域内的优化目标，通过求解累积回报的期望得到。Q＊k(s, a)是最优的状态-动作值函数，γ为折扣因子，r为状态-动作的立即回报。

回报函数包含燃油消耗量与电能的等效燃油消耗量之和，同时，为了维持SOC的平衡，在回报函数中加入了SOC惩罚函数。

其中：r(s, a)表示当前状态与动作的回报函数，mfuel为当前状态与动作的发动机燃油消耗量，me为电能等效燃油能量，β为权重系数，SOCref为SOC的参考值。

为了保护电池，防止其过充或过放，需将电池的SOC限定在参考范围内。在优化过程中，转矩、转速等因素也会对优化结果造成干扰，因此，在预测时域k～k+np对相关变量做如下约束：

其中：ne(k)表示k时刻的发动机转速；ne_max(k)、ne_min(k)为k时刻发动机转速的最大、最小值；Tm(k)为k时刻的电动机转矩；Tm_max(k)、Tm_min(k)为k时刻电机转矩的最大、最小值；Te(k)为k时刻的发动机转矩；Te_max(k)、Te_min(k)为k时刻发动机转矩的最大、最小值；Pm(k)为k时刻电动机功率；Pm_max(k)、Pe_min(k)为k时刻电机功率的最大、最小值；Pe(k)为k时刻发动机功率；Pe_max(k)、Pe_min(k)为k时刻发动机功率的最大、最小值；SOC（）为k时刻电池的荷电状态SOC。

3） 初始化状态动作值函数Q(s, a)，设置探索率ε、学习率α、折扣因子γ等参数以及迭代次数N。

4） 基于构建的目标函数，根据当前k时刻的状态s，利用ε-greedy策略（式17）探索预测时域np内的动作a（Tm(k+ 1 /k，Tm(k+ 2 /k)，…，Tm(k+p/k))）与环境进行交互，产生新的状态s′，同时获得当前状态-动作对的立即回报r。

5） 基于greedy策略评估回报以此来选择对应最小状态-动作值函数Q(s′, a′)的动作a′，通过公式（18）更新状态-动作值函数Q(s, a)值。

6） 迭代循环优化，根据设置的阈值0.01判断相邻迭代次数的策略是否收敛，策略收敛后，计算整车等效燃油消耗量。

7） 判断是否达到迭代次数N，若是，迭代循环结束，选择目标函数最优所对应的策略作为最优策略，也就是最优的转矩分配序列；否则，继续迭代。

2.3 反馈校正模型

根据2.2节的滚动优化过程可以获得当前k时刻的最佳电机转矩分配序列[Tm(k)，Tm(k+ 1 /k)，…，Tm(k+np/k)]，在实际控制中，只将最优转矩序列的第1个值Tm(k)作用于车辆。在k+ 1时刻，首先检测车辆的实际车速及加速度输出值，刷新预测模型，对未来有限时域内的车辆加速度进行重新预测，基于更新的预测值重新优化转矩分配。在每一个时刻都重复上述3个步骤，直到预测时域结束，即可获得预测时域内的最优转矩分配序列。

综上所述，采用模型预测控制方法求解超轻度混合动力汽车的能量管理问题就是在预测时域内，在每一时刻都重复“预测模型-滚动优化-反馈校正”3个步骤，即可获得最优的转矩分配，具体流程如图8所示。

3 仿真结果分析

基于MATLAB/Simulink平台，构建Markov链+ Q-Learning整车控制策略模型，以ECE_EUDC、UDDS标准循环工况为仿真试验工况数据，选取预测时域p为5 s , 仿真步长为0.01 s，SOC初始值为0.6进行仿真分析，通过仿真得到电机/发动机转矩分配序列及动力电池SOC变化情况。

为更直观了解电机转矩及发动机转矩的最优分配，在离散车速为35km/h的情况下进行仿真，得到每对状态-动作对对应下的最优动作策略，如图9、 图10所示。从图中可以看出，SOC对转矩分配影响不大，而需求功率的变化对转矩分配有重要的影响。当需求功率Preq较大时，车轮处的转矩由发动机提供，汽车一般运行在纯发动机模式；反之，电动机转矩足以提供车轮需求转矩，汽车则运行在纯电动机模式。这是因为Q学习算法在优化状态的动作时，不同车速下的转矩分配同时受到整车燃油经济性与动力部件参数的约束，不同的转矩分配影响整车的工作模式。

针对不同离散车速，可以获得需求功率、电池SOC所对应的发动机转矩和电动机转矩MAP图。采用插值可得到相应的优化解。为验证本文提出的Markov链 + Q-Learning的能量管理策略的有效性，将仿真结果与Markov链 + DP的能量管理策略进行对比。

分别从发动机、电动机输出转矩，动力电池SOC变化曲线，燃油消耗量，仿真时间这些方面对Markov链 + Q-Learning、Markov链+DP控制策略进行对比分析。

图11 a表示ECE_EUDC+UDDS工况数据图，图11b-图11d分别表示2种控制策略获得的发动机转矩分配、电动机转矩分配和SOC轨迹曲线。从图11b和图11c可以看出，两种策略的发动机转矩曲线接近，电动机转矩分配有差别，主要因为，电能的变化发生于纯电动模式和行车充电模式，Markov链 + Q-Learning控制策略中等效因子对这些模式下的电动机转矩进行了调整。对应到图11d中，Markov链 + DP控制策略的SOC终止值为0.598 6，ΔSOC = 0.001 4；Markov链 +Q-Learning控制策略的SOC终止值为0.598 7，ΔSOC= 0.001 3。与Markov链 + DP控制策略相比，Markov链 + Q-Learning控制策略的SOC变化量减少7.1%。

图12 显示了两种控制策略下发动机和电动机的工作点。从图中可看出，两种控制策略下发动机基本工作在最小燃油消耗率曲线上，电动机大部分工作点位于0.7～0.95的高效率区间内，说明本文所提出的Markov链 + Q-Learning的控制策略具有良好的控制效果。

ECE_EUDC+UDDS循环工况总行驶里程为22.92 km，Markov链 + Q-Learning 和 Markov链 + DP 这2种控制策略的百公里燃油消耗量分别为5.370 2 L和5.160 5 L。与Markov链 + DP的控制策略相比较，本文所提控制策略的整车等效燃油消耗量提高了3.9%。主要原因是DP和Q学习算法存在本质上的区别。DP算法在选择动作时是进行多阶段决策获得预测时域内全局最优的动作序列；而Q学习算法在选择动作时，通过ε-greedy策略尽可能地探索所有动作，更新状态-动作的Q值，获得预测时域内最优的动作序列，因为ε探索率是根据经验设定的值，所以得到的动作序列是全局次优，动作的选择会影响整车的燃油经济性。Markov链 + DP控制策略，采用多阶段决策来获得最优的转矩分配，在决策过程中计算目标函数，当所有阶段迭代完成后才更新策略。通过离线运行出数值表，数值表在线插值，仿真在线运行时间为10 s； 本文提出的Markov链 + Q-Learning控制策略，在优化时将时域状态转化为空间域，在优化状态的转矩分配过程中，迭代更新Q表的同时，策略也随时更新，仿真在线运行时间为6 s，最大程度提高了程序运行效率，提高了实时性。

4 结 论

提出基于Markov链与Q-Learning的能量管理控制策略。选用ECE_EUDC+UDDS标准循环工况数据为样本数据构建多步Markov模型对预测时域内的加速度进行预测，获得准确的预测结果；采用Q-Learning算法对预测信息进行滚动优化求解；施加第1个控制量给车辆，实现反馈控制。

基于Matlab/Simulink平台，构建ECE_EUDC+UDDS整车仿真模型。将仿真结果与Markov链 + DP控制策略进行对比，验证了该策略的有效性。Markov链 + DP控制策略对比，所提策略动力电池SOC变化量减少7.1%，变化较为平稳，在保证燃油经济性基本保持一致的前提下，仿真时长缩短了4 s，验证了该策略的适应性。

本文将控制理论与Q-Learning算法有效结合，实现了超轻度混合动力汽车良好的优化控制效果，在提高计算效率的同时，能够确保整车的燃油经济性。