AEB制动对THOR 50th假人乘坐姿态影响

孙振东，朱海涛，彭伟强

（中国汽车技术研究中心有限公司，天津 300300，中国）

随着汽车主动安全系统的应用，主被动安全融合已成为行业技术发展趋势[1-2], 其中自动紧急制动系统（autonomous emergency braking , AEB）是预碰撞阶段提高汽车安全性的重要技术。通过雷达或摄像头来探测前方突如其来的情况，若驾驶人不能做出相应反应，AEB系统就会强行采取制动来规避碰撞或减轻碰撞程度[3-8]。AEB虽然可以避免碰撞事故或者降低碰撞有效速度，但在其工作过程中，会产生相应的制动减速度，车内乘员由于惯性作用，会出现前倾离位现象[9-10], 现有乘员约束系统一般会在乘员正常坐姿下发挥最优保护效果[11-13]，但这种离位现象降低了约束系统的保护效能，增加了乘员损伤风险[14]。

S. Ejima 等利用志愿者研究了人体在紧急制动过程中的乘员动态位移情况[15]；清华大学许述财等根据欧洲儿童乘员约束系统法规（ECE R129）要求，建立台车座椅约束系统模型，施加法规中规定的速度曲线以模拟汽车在侧面碰撞事故中后排儿童乘员的头部损伤情况[16]。湖南大学曹立波等研究了主动式安全带参数对乘员碰撞阶段伤害影响，得出在相同碰撞强度下，AEB系统介入会影响乘员离位姿态，增加乘员损伤风险，尤其是胸部损伤[17]；重庆理工大学胡远志等通过实车道路试验，对志愿者在AEB制动下的运动响应进行分析，用于对标主动人体模型仿真精度[18]；湖南师范大学吴俊等通过座椅台架试验，运用HIII 50th假人对标实车道路实验中志愿者在碰撞前的姿态，分析了集成主动预紧式安全带（Integrated active pretension seatbelt）对乘员离位效果的保护[19]；黄福俊等研究表明乘员离位坐姿将显著增大碰撞过程中的人体损伤，安全带主动预紧的介入将有利于减少制动阶段的织带松弛量，进而大幅降低人体上身 (尤其是头颈胸等部位) 的纵向离位[2]。上述研究主要是基于真实人体在AEB制动时的前倾响应，而乘员姿态、肌肉支撑和乘员避险动作等会对前倾量产生影响。

新型THOR 50th假人具有与真人一样的外形，内部还设计了复杂的脊柱、肋骨和先进的合成肌肉，在人体生物力学响应上与真人更为接近，相比于HIII 50th假人更能满足AEB作用后离位姿态的要求，是气囊、安全带等约束系统标定试验中重要的测量工具之一。

因此，本文以新型THOR 50th假人作为对象，研究了AEB不同制动工况下的制动策略，对波形特征参数进行提取，用于试验系统预制动波形输入；设计了预制动减速度系统以模拟AEB的制动过程，通过简化台车搭载乘员乘坐环境，研究了不同制动方式下THOR 50th假人离位特征。本研究能为开发适应AEB作用工况下的乘员约束系统提供依据。

1 典型AEB制动波形建立

1.1 AEB制动工况分析

AEB系统性能测试通常有前车静止（car to car rear stationary，CCRs）、前车慢行（car to car rear moving，CCRm）和前车制动（car to car rear braking，CCRb）。

在以新型THOR 50th假人作为对象的测试中，CCRs、CCRm、CCRb这3种测试工况如图1中所示。

在CCRs测试工况中（见图1a），在测试车辆行驶路径前方放置静止目标物（VT），车辆分别以 20、30、40 km/h的速度测试AEB功能。

在CCRm测试工况中 (见图1b)，测试车辆和VT均沿规划路径行驶，VT以20 km/h 的速度匀速行驶，车辆分别以30、45、65 km/h的速度测试AEB功能。

在CCRb测试工况中（见图1c），测试车辆和VT均以50 km/h 速度沿规划路径行驶，车距分别为12、40 m，VT需在1 s内将减速度达到4 m/s2，误差不超过±0.25 m/s2。

基于上述3种工况对3款车型的AEB制动信号进行采集，如图2为采集的实车制动波形。

从图2中可以看出，基于AEB各制动波形均近似梯形波，除车型C在CCRb-40 m工况下采用双级制动波形，其余各车型和工况均采用单级制动波形；对于CCRs、CCRb-12 m 这2种工况，由于前方车辆静止或者跟车距离较近，车型采用快速的制动脉冲；对于CCRb-40 m和CCRm工况，车型采用较长时间历程的制动波形。

1.2 典型波形构建

车辆AEB制动主要分为4个阶段，分别是系统反应阶段、制动器起作用、制动器持续制动和放松制动的过程。因此，AEB系统制动波形可以用理论模型进行简化模拟，从而提取特征参数。

常用曲线的拟合方法有插值法、磨光法和最小二乘法。插值法是函数逼近的基本方法，是通过函数在有限个点出的取值情况，估算出函数在其他点处的近似值；磨光法是适应保凸性要求的数据拟合方法，可以将函数近似还原，同时可以更为光滑，常用于外形设计；最小二乘法是函数逼近的一种基本方法，该方法不要求拟合曲线通过已知点，而是通过最小化误差的平方和寻找数据的最佳函数匹配[20]。

由于制动波形中数值节点获取值不可避免带有测量误差，因此如果要求拟合曲线精确无误通过所有点，曲线将会保留一切测量误差，同时因所测数据点较多（采用频率10 K），采用插值法将得到次数较高的插值多项式，缺乏实用价值；采用最小二乘法拟合方法，可以避开上述弊端，得到一条使数据点在曲线附近分布的函数，该函数既能反映数据的总体分布，又不会出现局部较大波动，同时可以反映被逼近函数的特征。

因此，根据最小二乘法原理，将实测值yi与计算值y差值平方和最小作为优化的判据，即∑ (yi-y)2最小，根据图3梯形波曲线和原曲线可以建立相关差值方程。

其中：A为等效梯形波的峰值，tN为梯形波第1个时间拐点，tM为梯形波第2个时间拐点，tf为梯形波回零时刻。当差值方程最小时，它们分别对A、tM、tN的偏导数为零，可以得到式（4）。

在 MATLAB 中建立上述方程，采用最小二乘法对6款车型，16次AEB制动波形进行拟合。计算出A、tN和tM、进而得到梯形曲线，得到以下3类典型AEB制动梯形波：

在CCRs、CCRb-12m 这2种工况采用紧急制动脉冲时，拟合出图4制动梯形脉冲1。根据收集到的AEB制动波形得出制动幅值A在7 ～ 10 m/s2范围内，t1在0.2～ 0.4 s之间，t2在0.5 ～ 0.75 s之间。

对于CCRb-40m和CCRm这2种工况，拟合出图5制动梯形脉冲2。根据收集到的AEB制动波形得出制动幅值A在7 ～ 10 m/s2之间，t1在0.2 ～ 0.4 s之间，t2在为1 ～ 1.4 s之间。

对于车辆初始速度较高的工况，AEB采用图6中的双级制动策略。根据收集到的AEB制动波形得出较大的制动幅值A1在8 ～ 10 m/s2之间，较小的制动幅值A2在2 ～ 7 m/s2之间，t1在0.2 ～ 0.9 s之间，t2在2.2 ～ 2.8 s之间。

进行简化波形提取后，可以得出的AEB制动波形的关键参数，分别是峰值amax、持续时间Δt和速度改变量Δv，统计分析可以得出最大制动减速度和制动时间关系，如图7所示。

对提取得到的参数进行正态分布统计分析，可以得出最大制动减速度的分布如图8所示，制动平均减速度7.6 m/s2，对应制动时间约为1.28 s。

2 AEB制动波形复现测试平台

2.1 测试方案

将试验台车通过驱动装置连接至牵引系统（如图9所示）上，牵引系统由钢丝绳、牵引钩、驱动滑车、驱动电机、控制系统和测速装置等组成。根据所获得AEB系统典型制动波形，牵引控制系统中设置相应参数，确定相应试验台车位置。在牵引系统制动末端，驱动装置与试验台车分离后，启动试验台车电动制动系统，试验台车进行制动。

2.2 控制硬件

采用传统碰撞系统牵引轨道（长度大于150 mm）、导向机构和张紧机构；对减速滑车结构进行改造，采用一前一后主从牵引滑车。由于减速与加速牵引工况受力状态相反，且制动力为驱动力的1.4倍，因此需要对钢丝绳性能进行性能分析；同时需要研制一套新的牵引驱动系统，配备电机、电控、测速装置及安全防护逻辑开关等。

根据牵引目标运动曲线特征，计算各阶段对应加速度（表1），通过转动惯量评估各部件质量后，计算可得所需驱动力、驱动扭矩。得到减速工况复现过程中总扭矩为5 536 Nm ，需要提供18 kN的加速力和24 kN的反向制动力。由此确定驱动系统布局，并进行驱动轮、驱动轴承和电机性能参数计算与强度校核。

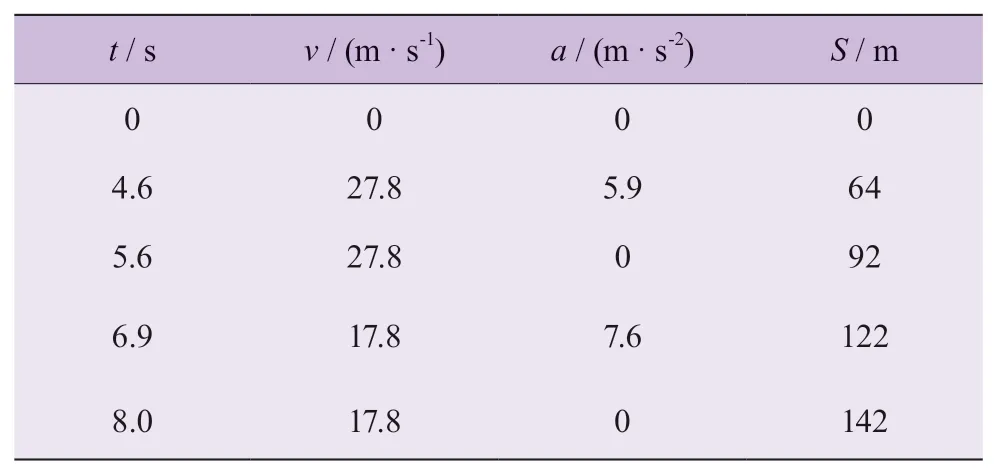
表1 系统制动过程阶段加速度

2.3 控制方案

控制系统以双闭环比例、积分、微分（proportion integration differentiation，PID）调节器为基础，分别对转速和电流进行负反馈控制。通过获取车速信号计算出与当前给定量的偏差以及偏差变化率，经过模糊推理和模糊决策确定调节参数。经PID运算后，输出到电流PID，然后由电流PID控制电机输出，形成闭环（图10）。通过PID 参数模糊控制方案，实现了传统双电机主从传动控制下，牵引系统自身输出速度与设置目标速度之间的同步性。

其中：ST为转速调节器，LT为电流调节器，SF为测速发电机，LH为电流互感器，Ugn、Ufn为转速给定和反馈电压，Ugi、Ufi为电流给定和电流反馈电压。

3 试验验证及结果分析

在试验台车上配置座椅和安全带系统，安装电动制动系统。将座椅调整至前后行程的中间和靠背角25°的位置，放置THOR50th假人。

THOR 50th假人佩戴限力式安全带，调整至正常坐姿位置。在假人头部、手臂及胸部粘贴高速影像分析用识别标志，右侧安装车载高速摄像系统，左侧安装坐标参考面（如图11所示）

试验台车分别达到20、30、40 km/h后分别施加0.7g和1g的减速度，直至试验台车静止，牵引系统6次试验的输出信号如图12所示。图12中试验1为台车加速到20 km/h，系统模拟单级制动脉冲，最大制动加速度为0.7g；试验2为20 km/h速度下，双级制动脉冲，最大制动加速度为1g；试验3，4为台车加速到30 km/h，系统分别进行单级和双级制动，最大制动加速度分别为0.7g和1.0g；试验5，6为台车加速度到40 km/h，分别以单级和双级策略进行制动。在上述试验1 ～ 6过程中，假人头部和胸部向前最大位移量如图13所示。

从图13分析中，可以得出：当速度小于30 km/h时，在相同初始速度下对台车进行制动，最大峰值为1.0g的双级制动波形与最大峰值0.7g的单级制动波形相比，造成THOR50th假人头部和胸部的前倾程度更大；当初始速度达到40 km/h时，假人前倾趋势发生变化，40 km/h-1g试验条件下的假人头胸前倾位移反而小于40 km/h-0.7g。台车在最大峰值0.7g单级制动波形工况下，假人前倾过程中安全带未发生锁止，而在峰值为1.0g双级制动波形工况下，安全带发生紧急锁止，导致试验6中的头胸位移量要比试验5中更小。对于不同初始速度下，以最大峰值为0.7g进行单级波形制动，初始速度越大，假人的头胸部离位程度越高，在以最大峰值1 g进行双级波形制动时，假人离位姿态变化趋势不太明显。

4 结 论

本文针对AEB制动工况下对THOR50th离位程度进行量化研究。首先对3款车型AEB系统在前车静止（CCRs）、前车慢行（CCRm）和前车制动（CCRb）3种测试工况中的制动波形进行采集；其次运用最小二乘法，对波形特征参数进行提取，对于CCRs、CCRb-12m 这2种工况，由于前方车辆静止或者跟车距离较近，车型采用快速的制动脉冲；对于CCRb-40m和CCRm工况，各车型采用较长时间历程的制动波形；对于车辆初始速度更高的工况，也会采用双级梯形波形；最后，通过预制动牵引系统，复现典型制动波形，分析了THOR50th假人坐姿离位情况。结果表明，当台车初始速度低于40 km/h，制动过程中安全带未发生锁止时，在相同初始速度下，减速度越大，THOR50th假人头部和胸部前倾量越大；在相同制动加速度下，随着初始车速的增大，假人头部和胸部位移逐步增大。在上述6种模拟AEB制动工况中，THOR50th假人头部和胸部最大前倾量分别达到320、178 mm，为约束系统的开发研究提供了参考依据。