半球形多向波聚合波道振荡水柱气室优化设计❋

杜小振， 常 恒， 赵 岩， 王 宇， 郝振富

(山东科技大学机械电子工程学院， 山东 青岛 266590)

振荡水柱(Oscillating water column 简称OWC)波浪能采集技术是利用起伏的海浪引起气室内液面上下振荡，再转换为空气动能驱动空气透平系统发电输出电能。主要研究方法为理论与数值水槽模拟和小型样机实验，结合入射波和海况条件设计最优气室结构。波浪作用于浮体的入射波分析：Vyzikas等[1]采用计算流体动力学(CFD)的物理场分析软件(Open FOAM)的开源程序库，研究了规则波和不规则波作用下数值波浪水槽内振荡水柱运动。Kuo等[2]模拟分析了作用于OWC箱式防波堤上的不同入射波水动力特性，研究了波长比与空气压缩动力之间关系。Wang等[3]研究非线性波动和粘度对固定振荡水柱装置的水动力性能影响，确定流体非线性和粘性增加可提高空气输出动力。Medina-López E等[4]对较强的风暴气候及海床变化进行数值模拟，结果表明OWC的效率随海床特征尺寸增加而降低。气室结构参数设计研究：宁德志等[5]基于域内源造波技术的时域高阶边界元方法， 建立了二维时域的非线性数值波浪水槽模型，研究了前墙入水深度、厚度与气室宽度对结构共振和能量转换效率的影响。Ahmed Elhanafi等[6-7]搭建1∶50比例的海上固定式OWC模型，采用试验和仿真相结合方法研究了空气压缩与气室波浪俘获能力关系，同时分析了最大效率时入射波高与前墙吃水深度的关系。胡杭辉等[8]基于势流理论建立了二维完全非线性波作用下OWC装置的数值模型，总结了波高、装置吃水深度、气室宽度和墙体厚度对能量转换效率的影响。He等[9]将双气室OWC结构嵌入浮箱式防波堤扩大能量捕获带宽，研究波浪周期、吃水深度和腔室布置等对输出功率影响。Ahmed Elhanafi等[10]研究前墙吃水深度、气室宽度和动力输出(POWER-TAKE-OFF，PTO)阻尼对双气室OWC装置波浪能提取效率影响。海洋浮标多为圆柱形或圆锥形结构，波浪方向随风向、洋流、潮汐等不断变化，浮标式OWC波浪能捕获结构需具备多向迎波，为此，周宇等[11]提出可以吸收各个方向海浪的“蘑菇型”气室结构，讨论了气室宽度、外墙厚度和吃水深度对波面幅值变化和波能俘获系数影响。宁德志等[12]研究圆柱形气室内的自由表面振荡模式，较低吃水深度和增加腔室宽度可以增加共振频率扩大振荡频率带宽。目前，振荡水柱波浪能采集气室研究了入射条件、尺寸结构优化计算和仿真分析，结构以固定单一方向波浪能采集结构设计为主。为了提高浮标振荡水柱是波浪能捕获效率，本文提出半球形多向聚合波道迎波振荡水柱气室结构模型，研究提升远海点式吸收波浪发电效率方法。

1 波浪运动数值模拟计算控制方程

振荡水柱气室处于三维数值波浪水槽内，假定流体为黏性、不可压缩、自由流动，则数值波浪运动基本控制方程由连续性方程和动量方程组成[13]。

连续性方程：

(1)

动量方程：

(2)

(3)

(4)

式中： 流体密度u、v和w分别代表沿x、y和z方向的速度分量；μ为流体动力粘性系数；p为流体内部压力；g为重力加速度；t为时间。

采用流体体积法(Volume of Fluid，VOF)[14]追踪数值波浪水槽内气液分层两相流的两个流体交界面，以确定每个控制容积单元中流体(空气和水)的体积分数。体积分数连续方程：

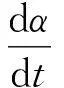
(5)

式中：U是速度矢量；α是水的体积分数，当α满足0<α<1时，控制容积单元中存在流体交界面。基于体积分数计算水气混合密度:

ρ=αρw+(1-α)ρα。

(6)

式中：ρw是海水密度；ρα是空气密度。

2 三维数值水槽仿真分析

2.1 半球多向迎波振荡水柱气室结构设计

振荡水柱气室优化设计可有效提高波浪能转化效率。以传统的振荡水柱波浪能采集气室设计原理为基础，提出半球形聚合波道多向迎波离岸式振荡水柱波能转换气室，气室上端形状能有效解决强海风作用下的发电装置的稳定性，气室内部增设后壁如图1(a)，三种不同开口角度(β=120°、90°和72°)波道后壁模型如图1(b)，探索多角度后壁的多向波采集技术，增加气室内压强、出气口速度等提高发电效率。

2.2 数值水槽和气室三维建模

利用NX.UG三维建模软件建立1∶1比例的振荡水柱气室及三维水槽模型，将气室模型置于数值水槽内部，计算区域模型如图2。

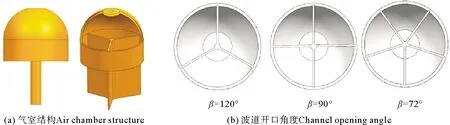
图1 半球形聚合波道多向迎波振荡水柱气室结构模型

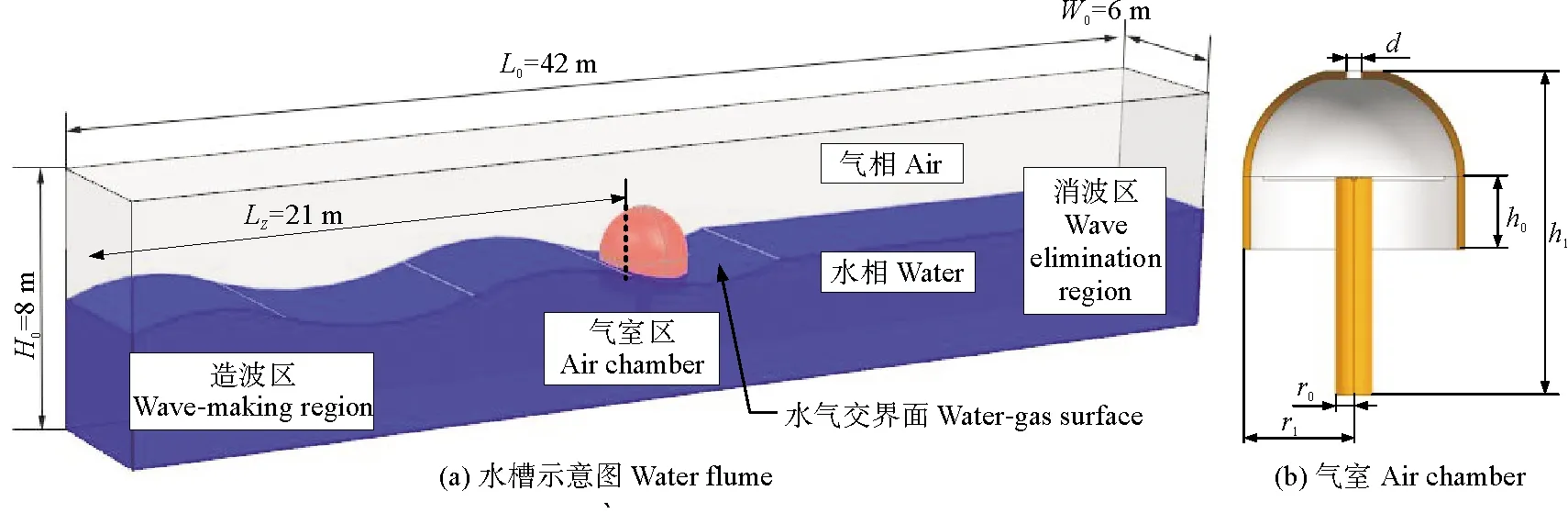
图2 三维数值水槽和气室模型

水槽长L0=42 m，宽W0=6 m，高H0=8 m(分为空气相4 m和水相4 m)。充分考虑造波区、消波区长度及水槽侧壁效应，将水槽宽度设置为OWC气室直径的2倍，气室中心距造波边界21 m，距水槽两侧壁面各3 m，气室底端距水槽底部0.5 m。在满足数值造波功能及计算准确性的基础上，合理设计模型的几何尺寸可以减少计算量，实现快速仿真分析，气室和数值水槽具体参数如表1所示。

三维数值水槽和OWC气室模型ICEM CFD结构化网格划分过程采用混合网格法，将水槽分为左侧造波区，中部气室区，右侧消波区；其中边界条件设置如图3(a)所示，水槽左侧造波边界设置为速度入口，右侧消波边界设置为压力出口；两侧面和底部边界均设置为固壁表面；顶部边界受恒定大气压力的影响，设置为压力入口；左侧造波区和右侧消波区为形状规则的长方体，故对其进行结构化网格划分，并将波浪运动区域做网格加密处理，如图3(b)所示；中部气室区需要装配气室，采用非结构化网格划分生成高质量的网格,如图3(c)所示。

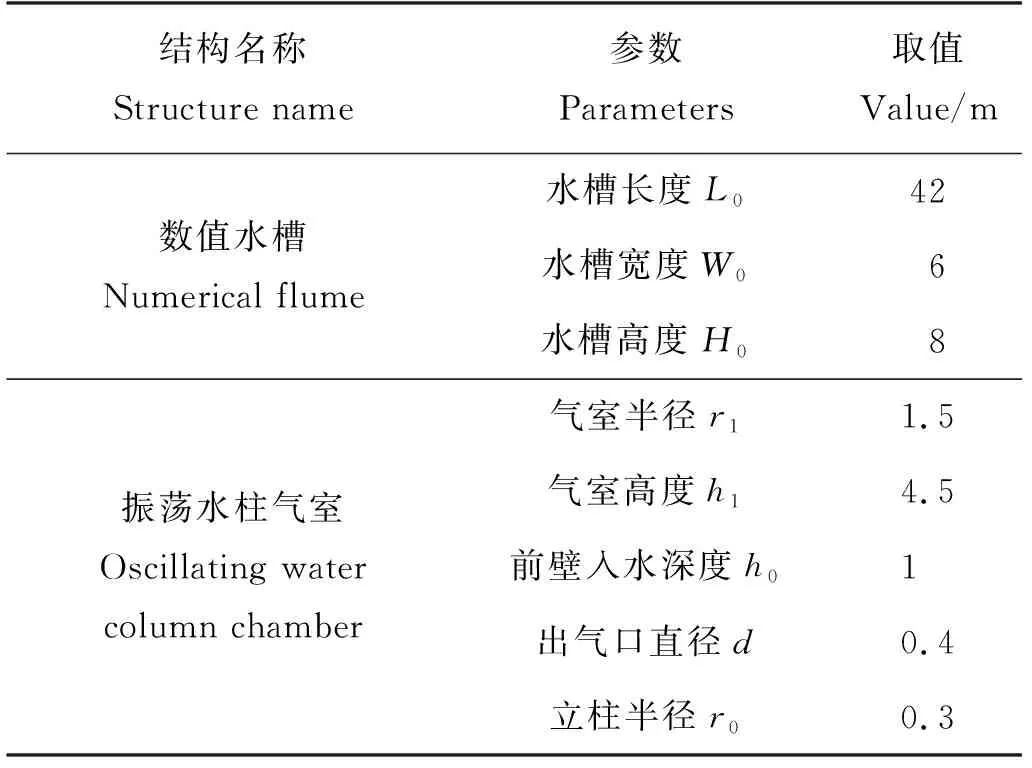
表1 三维数值水槽及气室结构参数

图3 三维数值水槽和气室网格划分

2.3 网格独立性验证

网格独立性验证，恰当划分网格，既保证数值模拟仿真精度又降低计算时间。模拟规则波正向入射，在Fluent中监测振荡水柱气室顶部压强进行收敛测试以确定合适的ICEM网格。因三维数值水槽的长度远大于其高度和宽度，文中仅改变x轴方向结构化网格数量，验证沿波长方向网格大小对仿真结果的影响，介绍四种接近收敛的结构化网格测试方案如表2所示。从方案1到方案4，气室造波区和消波区的结构化网格沿x轴方向逐渐加密，气室工作区的非结构网格设置全局网格尺寸系数(Scale factor)和最大网格尺寸(Max element)分别为2.0和0.1。

表2 结构化网格数量

四种不同网格密度计算所得的振荡水柱气室顶部压强曲线如图4，不同网格密度的压强分析结果保持一致；网格相对密集的方案2～4计算所得的压强峰值基本相同；网格数量较少的方案1计算所得压强略小于其它方案，平均误差约为8.9%且仅出现在波峰和波谷部分。因此，方案1网格较为稀疏，虽然能够模拟趋势，但计算精度较低，比较方案2与方案3和4，则保证精度条件下，本文数值水槽及振荡水柱气室仿真模拟研究均采用方案2划分网格。

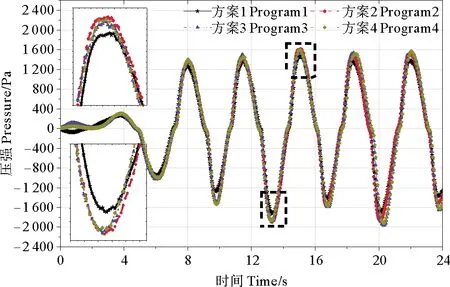
图4 网格独立性验证

2.4 数值水槽波形验证

基于VOF流体体积法及N-S控制方程建立三维仿真分析模型，波浪模拟采用流线弯曲、漩涡模拟精确的RNG模型，选择明渠造波法和多孔介质消波法分别实现造波和消波。根据渤海、莱州湾口等近海计算工况，仿真分析过程定义计算域内规则波的平均水深4 m、波高0.8 m、入射波周期3.5 s、波长17.179 5 m、湍流强度0.12%。利用分区标记功能(Region功能)划分空气和水的计算域，定义空气相为第一相，水相为第二相；利用Pach功能定义水的体积分数1。分别在距水槽左侧造波边界1、6、12和18 m处设置监测面，记录水槽和气室内波浪高度变化，位置如图5，设置仿真时间步长0.01 s，迭代步数4 000步。

图5 监测点和监测面示意图

在三维数值水槽中模拟二阶斯托克斯波，可通过设置在数值模型中的监测面1～4对水槽不同位置的波浪上升时间、波峰和波谷形状等波浪特性进行监控，对波浪稳定性、波高沿程衰减量及周期误差进行分析。对于波高H=0.8 m、波周期T=3.5 s、波长=17.179 5 m的非线性规则波，数值水槽4个位置的自由表面波高分别如图6(a)～(d)所示，将仿真模拟获得的数值波与二阶Stokes波的理论值进行对比，验证放置振荡水柱气室的数值水槽波形准确性。

对比同一监测面处数值波与二阶Stokes波的波形曲线，可知数值模拟波的自由表面高度随时间发展逐渐升高并接近于理论值，二者波浪周期基本吻合且波形均呈余弦变化。对比不同监测面处的数值波波形，可知监测面距离左侧边界越远，波形稳定所需时间越长，波浪高度沿程衰减越大。分别取16～30 s内x=1 m和x=18 m处波高的平均值，x=18 m处波浪高度较x=1 m处波浪幅值减小约14.33%，由于仿真模拟过程计入流体粘性作用和非线性影响，使得波浪在传播过程中存在数值耗散的衰减情况。综上，数值水槽中波浪高度的仿真结果和理论结果吻合，三维数值水槽模拟波高准确，可用于振荡水柱气室的仿真分析。

图6 数值波和理论波对比曲线

2.5 波浪与气室相互作用分析

数值模拟有限水深条件下振荡水柱气室与正向入射规则波浪的相互作用，将计算域内的空气相与水相分区并定义水的体积分数为1，得到数值水槽的体积分数云图如图7。上部蓝色区域为空气相，下部红色区域为水相，水气交界面清晰的展示了自由振动波面。观察自由表面的波形变化，左侧造波区形成周期性规则变化的波浪形状，右侧消波区波浪趋于平稳，数值水槽实现了有效的数值造波与消波。

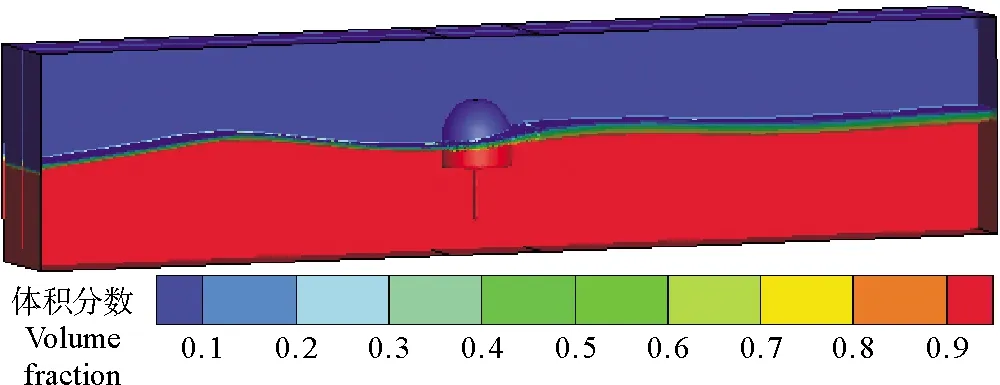
图7 数值水槽体积分数云图

为分析波浪与气室的相互作用，建立水槽中截面观察气室内外的自由液面变化，随时间变化每1/7波周期的体积分数云图如图8所示。观察图8(a)～(c)，随入射波波峰运动到中部气室区，气室外波面逐渐升高并向气室内传递，气室内波面随之升高，形成上升水柱；观察图8(d)～(f)，随入射波波峰向波谷过度，气室外波面逐渐下降，气室内波面也随之下降，形成下降水柱。但因气室外壁对波浪传播具有阻碍作用，气室内波面上升(或下降)的时间均晚于气室外波面上升(或下降)的时间。由上可知，气室内部水气交界面随波浪周期变化产生振荡水柱，实现了仿真过程中波浪与气室的相互作用。

当t=75 s时，数值水槽及振荡水柱气室内的流场涡量变化如图9(a)，设定参考涡量数值为0 s-1，整个计算域内流场的涡量均为正数，其中波峰、波谷、气室外壁及气室内部的涡量较大。因多相流仿真包含多种流体介质，所以分开讨论水域和空气域中的流场涡量变化，如图9(b)、(c)所示。水域中气室外壁底端涡量较大，这是因为气室外壁相对于水流的剪切运动产生大量涡量，在流体粘性作用下逐渐耗散；空气域中气室出气口处产生涡量较多，最大值为76.93 s-1，振荡水柱挤压空气发生旋转运动形成涡流，一部分通过出气口向气室外运动和耗散，另一部分在气室内部聚集成涡量团，涡量大小清楚显示出了在波浪与气室相互作用下流体速度场的旋度特征。

图8 气室每1/7波周期的体积分数云图

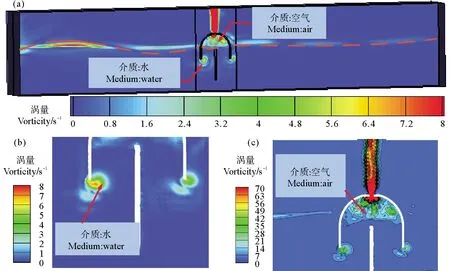
图9 数值水槽和振荡水柱气室涡量云图

3 气室模拟结果与讨论

在规则波条件下，数值波浪水槽模拟波浪作用于半球形振荡水柱气室，形成空气压强并且出气口速度随入射波进入气室逐渐增大，对表1所示的三维数值水槽及气室仿真参数计算结果显示，初次波浪进入气室5.0 s后气压趋于稳定的周期性变载荷状态。因此气室特性分析以此时间段后产生的压强和速度为主。研究气室后壁对半球形气室波浪俘获效率的影响，优化波道开口角度实现离岸式振荡水柱气室多向聚波采集技术。

3.1 气室气流运动特性分析

图7按时间顺序给出气室出气口的速度矢量图，显示了一个周期内气室出气口的速度大小和气流走向：图10(a)～(c)，气室内气体因入射波波峰进入气室受挤压排出，排气速度先增大后减小，随入射波波峰向波谷过度，气室由排气状态转换为吸气状态，气室内气流紊乱；图10(d)～(f)，气室内自由液面随入射波波谷进入下降，气室因内、外压力差变化开始吸气，吸气速度先增大后减小，最后因入射波波谷向波峰过度，气室内气流再次紊乱。

3.2 增设聚波后壁对气室性能影响

半球形气室中心迎波后壁对气室压强和出气口速度变化影响曲线如图11。在波浪稳定后不同气室结构的压强变化规律基本相同，压强幅值周期与入射波周期吻合，气室增设聚波后壁产生的空气压强显著高于无后壁气室结构，增设90°后壁时，波浪进入气室产生最大正压约为1 550 Pa，产生最大负压约为1 900 Pa。气室聚波后壁的加入有利于提高半球形气室出气口的速度，增设气室后壁后最大出气口速度可以达到53 m/s，这是因为增设气室后壁使波道口捕获的波浪增加，提高气室聚波能力，气室内波面振荡加强提高了空气压强和出气口速度。

图10 单周期内不同时间点气室出气口速度矢量图

图11 后壁对气室压强和出气口速度的影响

3.3 波道开口角度对气室性能的影响

假定各气室模型波道开口均朝向来波方向，气室数值变化规律基本相同；三种不同波道开口角度(β=120°、β=90°、β=72°)气室模型的压强对比曲线如图12，当β=120°时气室压强明显高于其它气室，波浪进入气室产生最大正压约为1 850 Pa，达到波谷时则产生最大负压约为2 300 Pa。气室出气口速度对比曲线如图13，气室正压峰值所对应的气室出气口最大速度为V120°>V90°>V72°，气室负压峰值所对应的气室出气口最大速度基本相同，减小气室波道开口角度将引起气室正压峰值对应的出气口速度降低，相邻速度峰值落差较大，不利于能量的收集。随波道开口角度减小，入射波集聚反射增加，波能捕获能力减弱。对比分析，气室聚波后壁开口β=120°时气室出气口气压速度稳定，有利于波浪能捕获和转换。

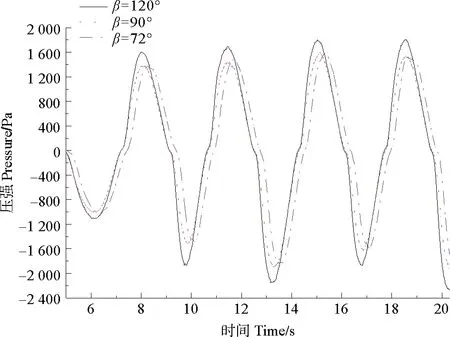
图12 气室压强与l迎波角度关系

图13 迎波角度气室出气口速度对比图

3.4 前壁形状对气室性能的影响

由振荡水柱气室涡量云图可知，前壁相对于水流的剪切运动产生大量涡量，部分能量在流体粘性作用下逐渐耗散。前壁作为波浪能转化装置的能量入口，合理的前壁厚度和入水深度可以有效减小能量损失，提高气室的波浪采集效率。选择最优后壁开口角度的基础上，选取4种前壁入水深度和3种前壁厚度两两组合，建立12种不同形状的前壁，如表3所示。在三维数值波浪水槽中对12种气室结构进行模拟仿真，对比研究不同前壁入水深度和不同前壁厚度对半球形振荡水柱气室工作性能的影响。

在相同规则波条件下分别对12种不同气室结构进行模拟仿真，得到三种不同前壁厚度下的气室压强和出气口速度变化曲线分别如图14～16所示。当振荡水柱气室壁厚分别为0.1、0.3 和0.5 m时，不同前壁入水深度下的气室压强和出气口速度曲线变化规律基本相同；气室壁厚保持一定，压强和速度均随入水深度的增加而不断减小，即三种壁厚的气室均在入水深度h0=0.5 m时获得最大顶部压强和出气口速度。例如，当振荡水柱气室的前壁厚度b=0.5 m保持不变时，4种不同入水深度下的气室顶部压强依次为Ph0=0.5 m>Ph0=1 m>Ph0=1.5 m>Ph0=2 m，出气口速度依次为Vh0=0.5 m>Vh0=1 m>Vh0=1.5 m>Vh0=2 m，入水深度h0=0.5 m的振荡水柱气室具有最大顶部压强1 804.50 Pa及最大出气口速度59.03 m/s。由上可知，在一定范围内减小前壁入水深度可有效减小波浪触壁反射的现象，提高气室顶部压强和出气口速度，增强振荡水柱气室的波浪俘获能力。

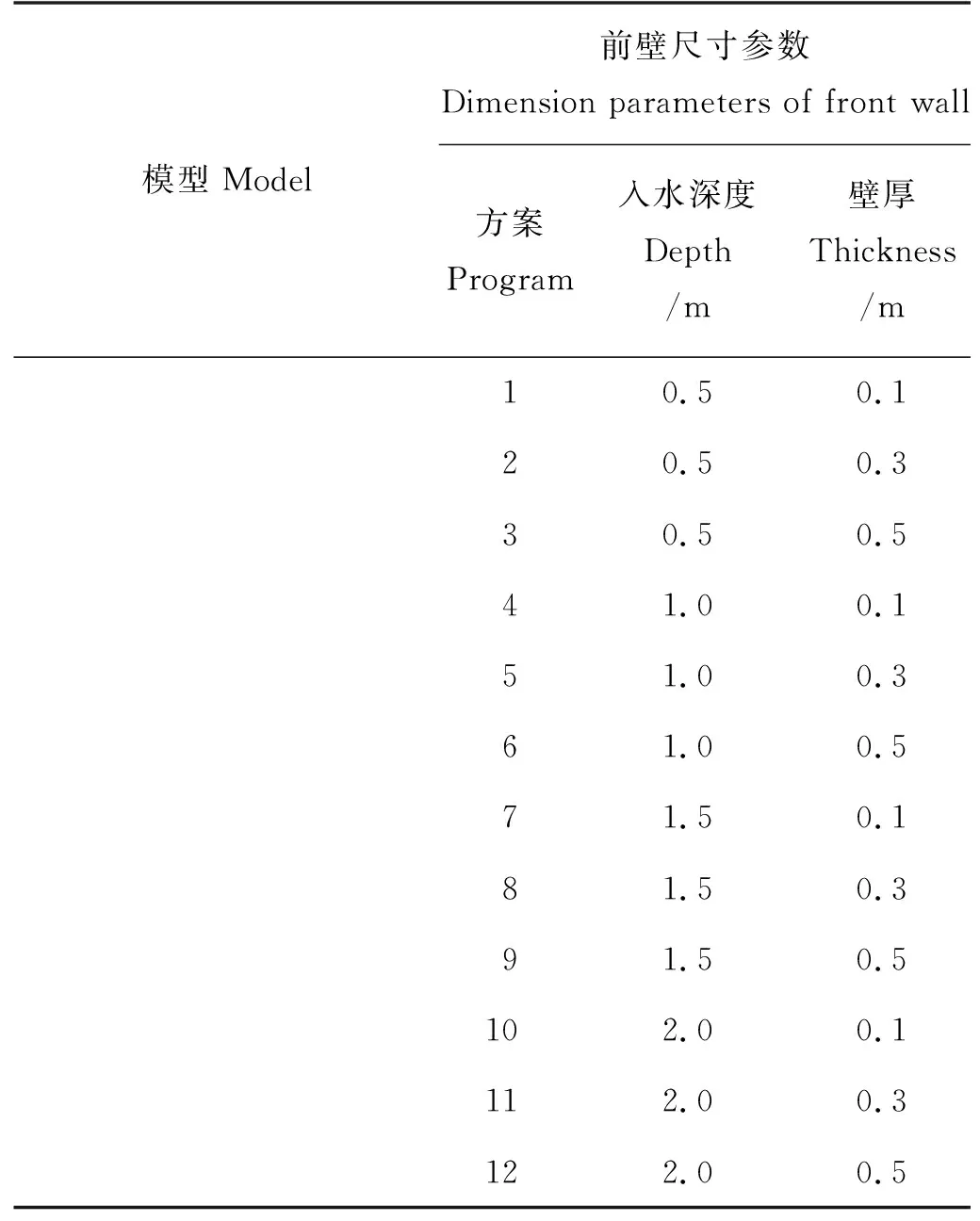
表3 气室前壁尺寸参数

当t=10.5～17.5 s时，3种前壁厚度及4种入水深度下的气室压强和出气口速度的最大值如图17所示。当前壁入水深度分别设定为0.5、1、1.5、2 m 4种情况时，相同波浪条件下的气室压强和速度均随气室壁厚的增加而增加，在壁厚为0.5 m时获得最大值。例如，当入水深度h0=0.5 m时，3种壁厚(b=0.1、0.3、0.5 m)气室获得最大顶部压强分别为1 697.88、1 798.21、1 804.50 Pa，最大出气口速度分别为50.42、57.10、59.03 m/s。由上可知，当前壁入水深度一定时，随气室壁厚的逐渐增加，仿真所得顶部压强和出气口速度均不断增大。

图14 前壁入水深度对出气口空气压强和速度的影响(b=0.1 m)

图15 前壁入水深度对压强和速度的影响(b=0.3 m)

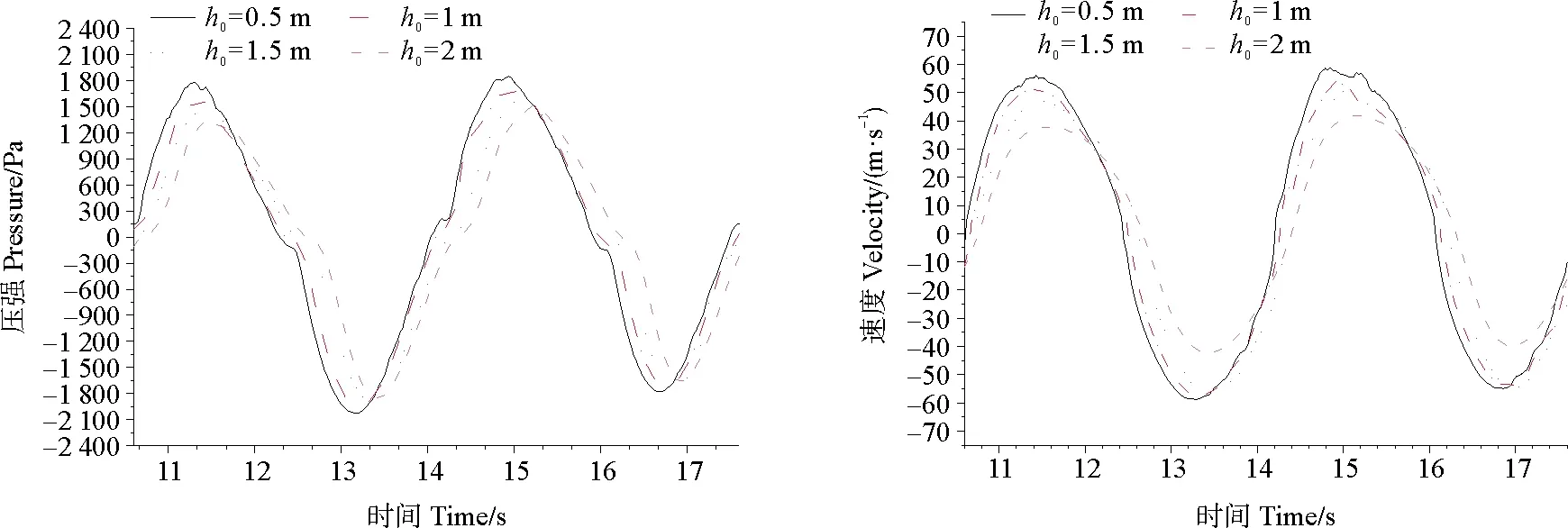
图16 前壁入水深度对压强和速度的影响(b=0.5 m)

由以上分析可知，增大气室前壁厚度或减小前壁入水深度，可有效减小波浪触壁反射形成的能量耗散，有利于提高振荡水柱气室对波浪能的捕获能力。对比12种前壁结构，当壁厚b=0.5 m、前壁入水深度h0=0.5 m时半球形气室结构最优，仿真获得顶部压强和出气口速度的最大值分别为1 804.50 Pa和59.03 m/s。

4 结论

在规则波正向入射条件下对半球形振荡水柱气室进行数值模拟，未考虑复杂的海洋环境。基于VOF流体体积法及N-S控制方程建立半球形振荡水柱波浪能采集三维数值水槽的模拟分析模型，利用数值模拟方法研究了半球形多向迎波振荡水柱气室能量俘获特点，依据分析结果分析了增设气室后壁、改变波道开口角度、优化前壁形状对半球形气室性能的影响。

(1)增设气室后壁的半球形气室的压强和出气口速度均有提高，气室对波浪能的俘获能力得到提升。

(2)减小波道开口角度将降低气室正压峰值和出气口速度，波道开口β=120°时气室压强最大、出气口速度稳定。

(3)增大气室前壁厚度或减小前壁入水深度，波浪触壁反射形成的能量耗散减小，振荡水柱气室对波浪能的捕获能力得到提升。