基于改进CNN-GRU网络的多源传感器故障诊断方法
2022-01-13马立玲郭建汪首坤王军政
马立玲, 郭建, 汪首坤, 王军政
(北京理工大学 自动化学院,北京 100081)
传感器是实现自动检测和自动控制的重要基础,实时准确的故障诊断在实际生产中具有重要研究价值[1]. 复杂系统需要更多的传感器,增加了故障发生的频率,多源传感器数据之间的耦合关系增大了故障诊断的难度.
数据驱动的方法凭借其适应性强、准确率高的优点在传感器故障诊断领域得到了广泛应用,具体可分为基于多元统计的方法[2-3]、基于信号分析的方法[4]和基于机器学习的方法等. 近年来,采用数据驱动结合机器学习的故障诊断工作取得了许多成果. HUNDMAN等[5]使用长短期记忆网络对时序数据建模来求取误差向量,并设计了一种自适应的误差阈值设定方法. CHENGLIN等[6]将SVM与混沌粒子算法结合,避免了诊断算法陷入局部最优问题. 谢迎新等[7]提出了一种结合变精度粗糙集(VPRS)和RBF神经网络的诊断方法,提高了对具有显著不确定性的无线传感器网络节点的故障诊断准确性.
运用数据驱动结合机器学习进行故障诊断时存在一些问题 :①故障诊断工作不全面,多数诊断算法只是实现了是否发生故障的判断功能,但无法获取故障的严重程度和故障参数. ②在采用深度学习的算法中常常会为了更高的准确率而增加网络的深度,导致运行速度下降,训练难度增加. ③诊断算法的运算复杂度高,不满足实时性要求. 针对以上问题,本文提出了改进式卷积-门控循环网络(CNN-GRU)架构,能够实时处理多源传感器数据,一次性准确得出故障类型和故障参数等信息,同时优化了网络的训练方式,使得网络快速收敛稳定,这一方法在多源导航传感器平台得到了验证.
1 基于改进式CNN-GRU网络的故障诊断策略
CNN-GRU网络的主体由卷积神经网络(convolutional neural network,CNN)和门控循环单元网络(gated recurrent unit,GRU)构成,CNN常用于图像的特征提取,GRU常用于时序数据预测,二者一般采用串联结构结合在一起,可用于序列数据的转换.
单一传感器数据是一维的时序序列,当使用多源传感器时增加了传感器种类这一维度,就构成了二维的时序序列. 不同传感器之间存在相互联系,例如用编码器检测到的车轮转速,在汽车的偏航角较小时应该与GNSS解算出的速度成正相关. 这种相互联系存在于在同一时刻或者很小时间段内不同传感器之间,称为为传感器数据的空间特征. 在数据上,通过二维数据的横向特征表现. 同一个传感器在时间上的变化情况也具有一定特点,包括变化率的幅值、变化的幅值、数据大小和符号等,这种特点称为传感器的时间特征. 在数据上,通过二维数据的纵向特征表现.
串联式CNN-GRU混合网络的诊断计算流程如图1所示. 首先将多条传感器数据统一为相同的采样频率,然后按照时间顺序对齐,拼接为二维矩阵的形式并进行切片化处理,然后利用CNN提取空间特征,时间窗口大小为T的传感器数据可以得到特征图(feature map),门控循环网络将特征图视为序列数据,可以进一步提取特征图的时序特征,最终得到故障信息.

图1 CNN-GRU网络的前向计算流程示意图Fig.1 The calculation process of CNN-GRU network
针对传感器与普通图像数据的区别,本文对串联式CNN-GRU混合网络进行改进,分别在卷积网络计算中加入传感器数据标定模块(sensor calibration),在循环网络计算中加入故障类别解析模块(fault class analysis). 传感器数据标定模块嵌入在卷积网络之中,根据模块之前的特征图,计算出每个传感器的权重参数,并作用在模块之后的后续计算中. 故障类别解析模块的作用是将一个网络进行复用,既负责故障类别的识别,又负责故障参数的估计. 故障类别解析模块提取循环网络的中间层特征计算出故障的类别信息,并进一步将类别信息解析,传递给负责参数估计的网络. 流程如图2所示.

图2 故障诊断算法整体流程Fig.2 Flow chart of fault diagnosis algorithm
基于神经网络的故障诊断算法属于有监督学习的一种,具体的算法步骤如下:
① 采集原始故障数据与正常数据,对数据进行归一化处理,然后切片为序列数据,并将处理后的数据分为两部分:训练集和测试集.
② 将训练集输入改进CNN-GRU网络中,调整网络的超参数,训练到损失函数满足要求或者训练固定轮数.
③ 输入测试集一个样本,根据GRU网络故障类别解析的数值判断测试数据是否为故障数据.
④ 如果数值为0,那么测试数据不是故障数据,取测试集的下一个样本.
⑤ 如果数值非0,那么测试数据是故障数据,则根据GRU网络末端输出的数值得到故障参数.
2 方法原理及实现
2.1 带有传感器标定模块的卷积神经网络
卷积是一种非常有效的特征提取方式[8],主要的运算对象为二维或三维数据. 计算方法为:给定一个尺寸为s×t的卷积核,使用图像长×图像宽×通道数的三维矩阵格式表示图像,将卷积运算应用在在图像的某一个通道上,神经网络中卷积的计算公式为
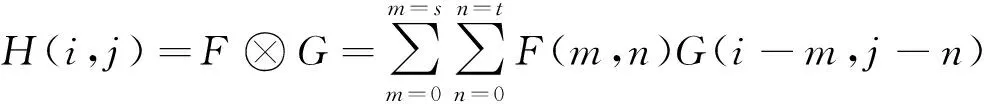
(1)
式中:H为卷积运算输出的特征响应;F为输入图像;G为卷积核;⊗表示卷积运算. 卷积核的参数决定了其提取特征的类型,较为初级的特征包括边缘和突变等,通过多层网络堆叠可以实现复杂特征的提取.
传感器数据与普通图像的区别是多路传感器数据之间的排列顺序是不固定的,采集到的数据X=[x1x2…xn]也可以排列成X=[xnx5x2…xm]的形式,而卷积神经网络是根据感受野范围去提取特征,这样与故障传感器排列距离较近的数据可能会更多地影响特征矩阵. 这种特征提取方式对于图像数据显然是合理的,但是对于传感器数据,排列距离最近的传感器并不一定是与故障传感器最相关的传感器,例如测量车轮转速的传感器发生故障时,惯性导航系统测量的偏航角参考价值就小于全球导航卫星系统GNSS测量的位置信息. 为了减小传感器排列顺序带来的干扰,本文设计了一个传感器标定模块,其结构如图3所示,传感器数据N代表采样点个数,n代表传感器个数.

图3 传感器数据标定模块结构Fig.3 Structure diagram of sensor data calibration module
如果在卷积网络中某一特征经常被激活,则使用全局平均池化计算的值会更大. 根据这一特点,本文在正常特征提取支路(左支)外附加了全局平均池化对n路传感器数据进行全局池化(右支),然后使用全连接网络构建一种非线性映射得到n路传感器对应的权重,将权重与基础特征相乘即可得到标定后数据.
事实上,如果只是进行权重的计算然后就执行乘法的运算会造成网络中特征的剧烈变化,从而降低网络的鲁棒性,因此池化层后面的全连接网络就不可忽略,它起到了在权重通道上进行适当调整的作用. 如果在运行速度要求不高的前提下,可以在标定传感器数据后再加入更多层网络进行解码,可以更好地提取传感器的特征以及相互依赖关系.
2.2 带有类别解析模块的门控循环网络
门控循环单元GRU是循环神经网络(recurrent neural network, RNN)的一种,有效缓解了传统RNN训练困难的等问题[9]. 循环神经网络使用循环核提取特征,循环核内的记忆体ht负责将不同时刻的信息传递下去. GRU的结构图如图4所示.
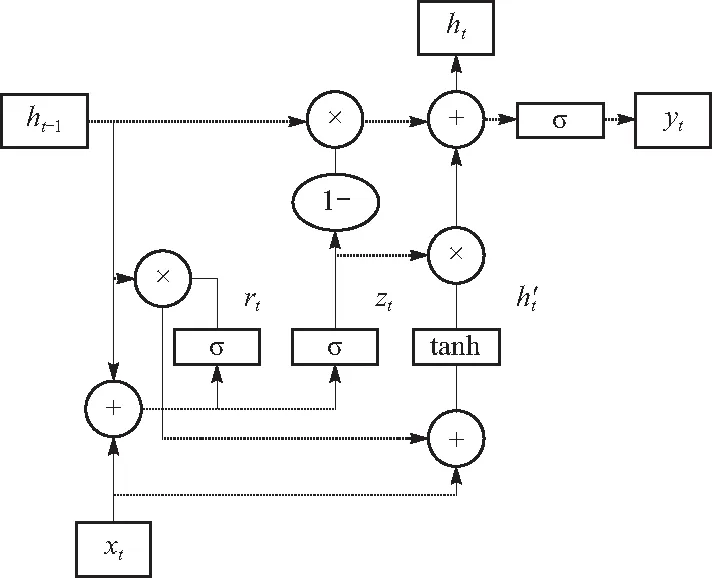
图4 GRU结构图Fig.4 Structure diagram of GRU
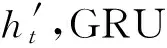
(2)
式中:σ为sigmod激活函数,将zt和rt限制在0到1之间,从而发挥门控的作用. 在记忆体信息ht的计算过程中既包含了过去数据的信息ht-1也包含了当前输入信息h′t,从而使得网络具有了记忆和遗忘的功能. 传感器数据就是一种典型的时间序列,将每个采样点的数据依次输入到网络中,训练之后网络就可以学习到某一种传感器数据之间在时间维度上的前后联系,进而完成分类预测等任务.
传统的深度网络采用直接堆叠的方式,如图5所示,左侧为堆叠形式,右侧为按照时间步的展开形式. 这种方式的缺点是输出方式单一,训练困难. 本文设计了一种具有类别解析模块的门控循环网络,通过跳跃连接和设置辅助函数的方式,降低网络的训练难度. 改进的带有类别解析的循环神经网络由两部分组成,主支路逐层的提取特征,主支路外附加的跳跃连接主要由平均值运算、全连接网络等组成. 故障的类别与故障的参数存在密切联系,例如固定偏差故障需要估计的参数为偏差的幅值,漂移偏差需要估计的参数为偏差变化的导数,因此在识别故障的类别之后,将类别信息传递到估计参数的主网络上将有利于整体的诊断性能. 故障类别的信息解析可以由全连接网络或者循环网络实现,当选择后者时可以将解析用的循环网络和参数估计的网络合并,最终带有故障类别解析的门控循环神经网络结构如图6所示.
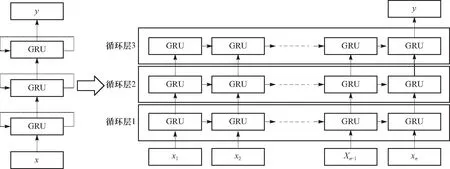
图5 传统多层循环神经网络结构Fig.5 Structure diagram of traditional multilayer recurrent neural network
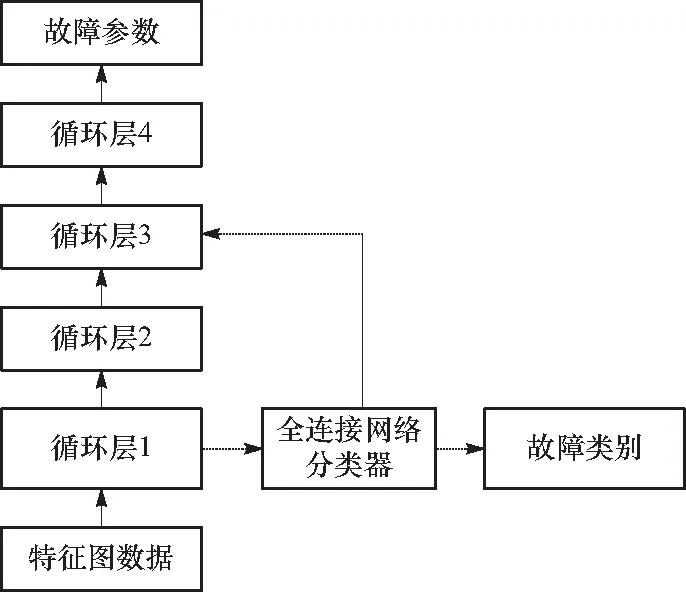
图6 带有故障类别解析的门控循环神经网络Fig.6 Gated recurrent neural network with fault class analysis
为了更加有效地训练这个网络,设计了一种动态损失函数
L=mcLc+mpLp
式中:Lc为交叉熵损失函数,用来衡量故障类别的准确程度,称作辅助损失函数;Lp为均方差损失函数,用来衡量故障参数的精度,称为主损失函数;mc和mp分别为二者的权重参数,在网络训练前期,mc
2.3 改进式CNN-GRU网络相关参数
网络的具体结构如图7所示:共使用了2个卷积层和4个循环层,在卷积网络和循环神经网络之间设置了数据处理层,用于将网络中的数据的格式进行转换,以满足循环网络的输入要求.
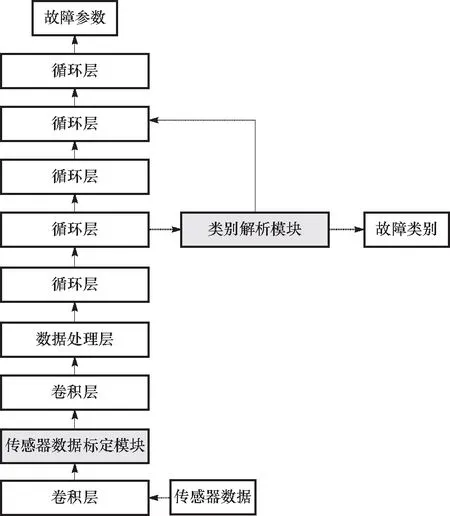
图7 改进式CNN-GRU网络结构图Fig.7 Structure diagram of the improved CNN-GRU network
网络的输入为传感器数据,输出为传感器故障类别和故障参数. 网络的参数设为:卷积核大小为2×2,卷积核个数为3,激活函数选择Relu函数,循环层神经元个数依次设置为80,100,100,50,时间步设置为60个采样时刻,按照20%的概率在每一层后设置随机失活. 损失函数为前文提到的动态损失函数,初始学习率为0.001,批次大小设置为64,默认训练次数为50轮.
3 实验验证及分析
3.1 实验数据
在汽车的导航系统中需要使用到多种类型的传感器,是非常适合多源传感器实验的平台. 本文依托于麻省理工大学的开源车载传感器数据,文献[10]对其有详细描述. 本文使用了其中部分数据,包括13路传感器,分别为x,y,z轴加速度,俯仰角,偏航角,横滚角,速度,高度,经度,纬度,车轮转速,x,y轴光流速度.
不同传感器的故障原因有所不同,但表现形式有很多共同点. 传感器故障可以分为4类:完全失效故障、漂移偏差故障、漂移偏差故障和精度下降. 固定偏差故障指传感器的测量值和真实值相差某一恒定常数的一类故障,漂移故障是指传感器测量值与真实值的差值随时间而变化的一类故障,二者都不易被发现,是本文主要关注的问题.
假设发生故障的传感器为第j路传感器,则
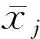
H=1
当发生漂移偏差故障时
H=2
故障的主要信息F包括故障种类和相应的参数即
F={H,k1,k2,t1,t2}
原始数据为正常驾驶数据,共有859条,通过注入故障的方式,最终得到859条正常数据,1 718条故障数据. 训练集和测试集数据划分的比例为8∶2.
3.2 算法训练
网络深度是影响神经网络的重要因素,网络过浅的缺点是学习能力不足,难以达到较高的准确率;网络过深的缺点是训练难度加大,易出现梯度消失现象,导致网络中的前几层缺乏有效的训练,最终网络的准确率也较低. 如2.2节中提到,本文通过设置跳跃连接,为网络在中层附近增加了一个辅助损失函数,与网络的末端损失函数进行复合,共同实现对网络的监督训练.
将改进式网络分别按照固定损失函数与动态复合损失函数进行训练,结果如图8所示. 采用固定损失函数的网络在训练40轮左右后逐渐稳定. 采用动态损失函数的网络,先按照主损失函数与辅助损失函数的权重比值为3∶1训练10轮,再按照1∶3训练15轮,其余阶段按照1∶1训练,在30轮左右接接近稳定. 对比可知,动态复合损失函数的设置可以有效缩减训练时长,本文提出的故障诊断算法避免了深度神经网络常见的训练困难的问题.

图8 改进式CNN-GRU网络使用不同损失函数的训练效果Fig.8 The training effect of the improved CNN-GRU network based on different loss functions
3.3 算法准确率
为简便描述,将本文提出的具有2项改进的CNN-GRU网路称为网络1,将仅仅改进了卷积网络部分的网络称为网络2,将仅仅改进了循环网络部分的网络称为网络3,将没有改进的CNN-GRU网络称为网络4. 首先比较网络的训练情况,如图9所示:4个网络都能够收敛,收敛精度上网络1的损失函数数值最小,网络2和网络3训练曲线介于网络1和网络4之间,网络4的训练过程存在剧烈震荡.
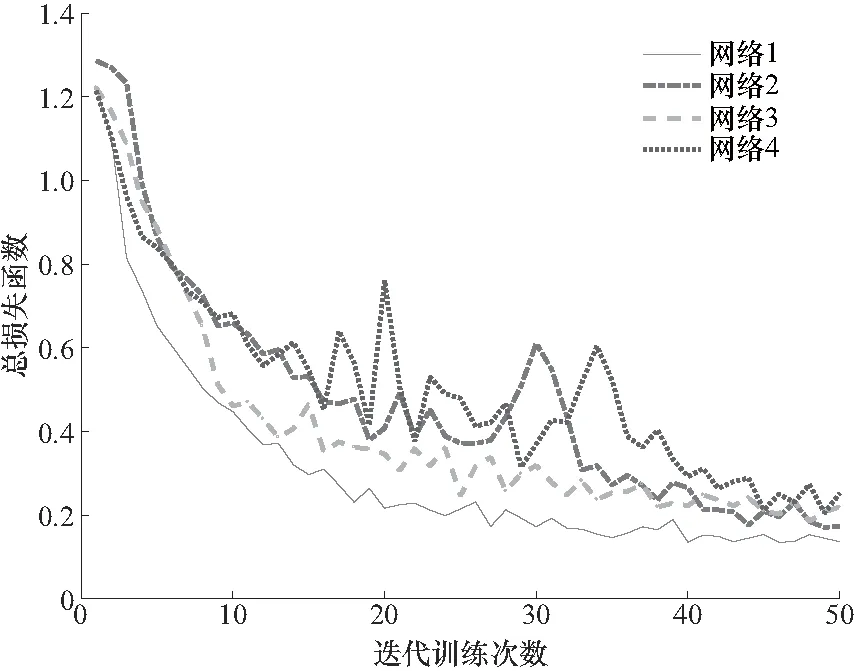
图9 不同网络的损失函数下降曲线Fig.9 Loss function decline curve of different networks
经过训练后,在样本数为188的测试集上对4个模型进行测试,统计故障类别识别的准确率. 如图10所示,网络1表现最好,在漂移偏差、固定偏差故障和总的准确率上都是最高的,网络4表现较差. 结果表明2项改进均有利于提高算法的准确率,并且它们的有益效果是兼容的,最终诊断算法的总准确率达到了98.9%,说明本文提出的故障诊断算法具有较高的准确率,可以应用于实际场景.
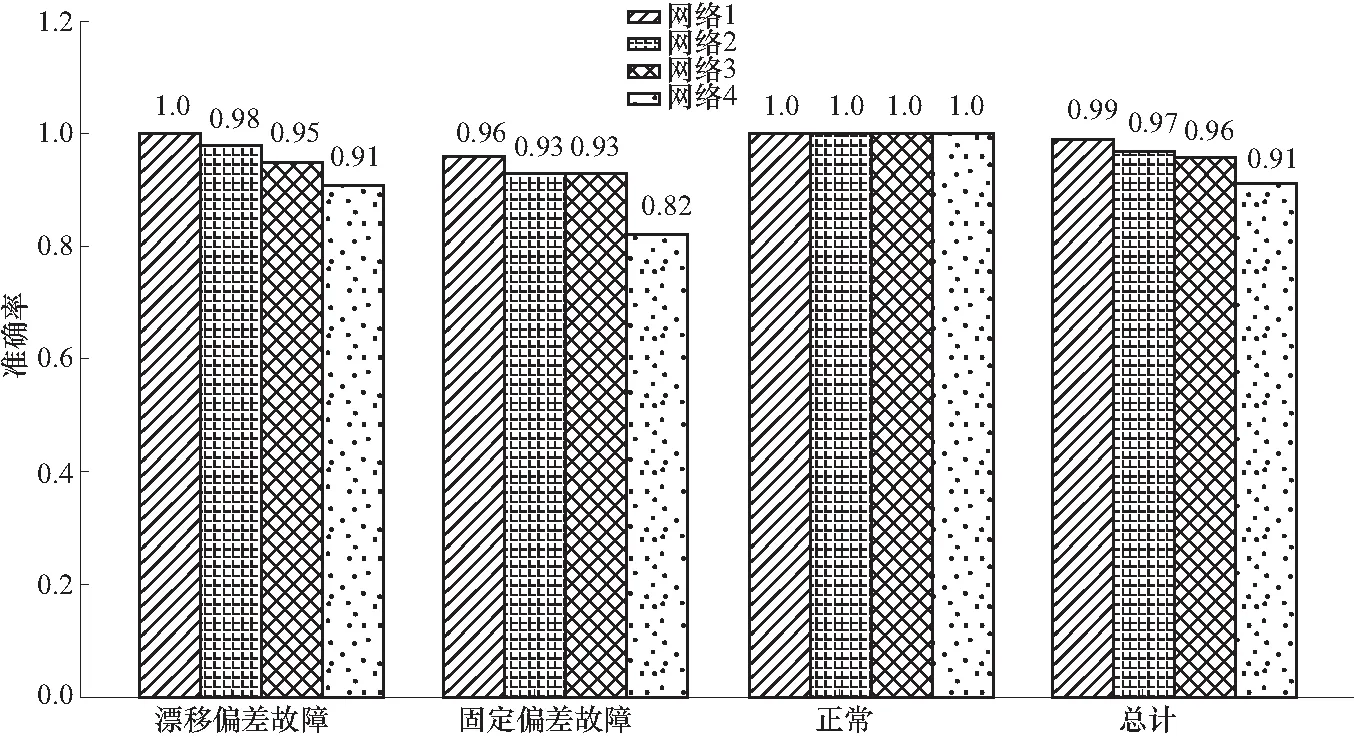
图10 不同网络的识别准确率Fig.10 Recognition accuracy of different networks
3.4 算法精度
算法精度指故障参数的估计精度,本文使用平均绝对误差(mean absolute error,MAE)进行评价,计算公式为
(3)
式中:yi为第i个样本的真实故障参数;hi为第i个样本的预测故障参数.
因为对于正常数据仅需要判断类别,因此仅统计两类故障的误差. 如图11所示,网络1的精度最高,误差最小,总计平均误差为2.18%,网络4表现最差,其平均绝对误差超过了10%,难以应用于实际场景. 由此可见,本文提出的故障诊断算法能够使用同一段传感器数据,一次性较好地完成故障类别识别和故障参数估计2项任务,是一种较为全面的故障诊断方法.
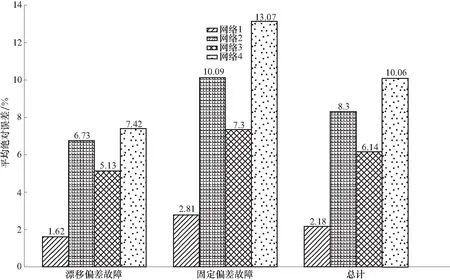
图11 不同网络的平均绝对误差Fig.11 Mean absolute error of different networks
3.5 算法运行速度
在网络结构设计中,本文通过减小卷积核尺寸,减少循环层神经元个数,减少网络层数,优化网络结构等方法降低了网络的参数个数,尤其是针对循环网络的改进,使得一个网络可以解决两类问题. 整体网络模型的参数数量为1.4×106,在实验环境下(Acer A3-572G电脑),网络每轮平均训练速度为28 s,网络可处理传感器数据帧率可以达到70 fps,考虑到数据集中的传感器数据采集频率仅为30 fps,可知本文提出的改进式CNN-GRU网络是一种实时的故障诊断算法.
3.6 算法鲁棒性
在精度和准确率测试中,训练集和测试集是具有相同分布规律的不同时刻普通故障采样数据,然而含有故障信息的传感器数据数量有限,因此在训练集和测试集中未能包括每种传感器故障的全部参数,而在实际环境中,故障参数的分布范围会更广,因此考察一个网络对于更大范围内的故障参数的表现是必要的. 本文使用普通故障的训练集进行训练,使用幅值为普通故障的150%的严重故障数据集进行测试,结果如图12所示:准确率为94.6%,平均绝对误差为4.23%. 网络在严重故障数据集上准确率和精度都有所下降,其原因主要是故障模式的幅值增大会严重影响原始传感器数据的变化规律,造成故障特征提取困难,但总体效果还是令人满
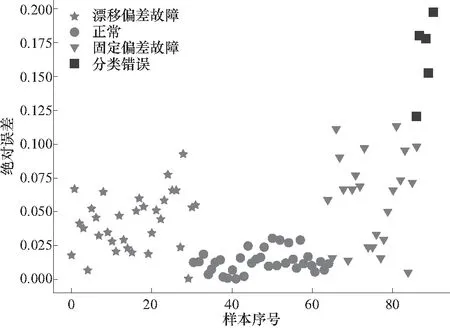
图12 在严重故障数据集上的误差情况Fig.12 Error on an untrained test data set
意的,证明了本文提出的诊断算法具有较好的鲁棒性,做到了根据学习的故障知识进行合理外推.
4 结 论
多源传感器的应用给故障诊断提供了更多的数据也带来了更多的约束. 为了发挥出多源传感器数据丰富的优点,本文首先设计了CNN-GRU基本网络模型,来充分的提取传感器数据中隐藏的时空特征. 为了提高网络的准确度和精度,本文从网络的前端和后端分别入手,分别设计了传感器标定模块来提高模型对传感器数据的鲁棒性和跳跃连接模块来增强类别信息和参数信息的互相联系,实验证明了2项改进通过不同方式提高了网络模型的性能. 最终改进式的诊断算法的准确率达到98.9%,参数估计的平均绝对误差约为2.18%. 改进式诊断算法是基于传感器的检测序列进行检测的,检测速率达到70 fps,根据同一批次数据就可以判断是否发生故障、故障类别和故障参数的诊断工作,具有实用价值. 在本文提及的方法中,网络结构中部分参数的选择方法有待做进一步的深入.
