复合材料夹芯板弯曲分析的双变量精确板理论
2022-01-13朱秀杰殷军辉邓辉咏邹有纯
朱秀杰, 郑 坚, 熊 超, 殷军辉, 邓辉咏, 邹有纯
(陆军工程大学 石家庄校区,河北 石家庄 050003)
格栅、波纹夹芯板具有轻质高强的特点,很早之前便在包装、建筑、机械和海洋工程中应用[1]。采用树脂基纤维增强复合材料制造的格栅/波纹夹芯板的结构参数和铺层参数的选择空间广阔,不仅能利用复合材料耐腐蚀性好、热性能好、阻尼减振性好等特性来满足多元化功能要求,更能发挥承载效率高的结构优势,最大限度减轻惰性质量。含有复合材料的格栅/波纹夹芯结构的应用领域尽管已经拓展到了飞机、运载火箭、人造卫星和水下潜航器等工作环境苛刻、轻量化要求高的高端装备上,但应用的限制之一就是力学性能容易受弯曲载荷引起的结构变形的影响[2-9]。计算此类结构弯曲刚度能指导初步设计,提供优化设计目标函数,确定等代改进、改型设计刚度参考值。
含有复合材料的格栅/波纹夹芯板在弯曲载荷下的力学特性备受国内外学者的关注。Shi等[10]综合采用四点弯曲试验、解析计算和有限元模拟的方法确定并比较了C/C-SiC复合材料格栅夹芯板的跨中挠度;Fatih等[11]利用声发射技术监测了整体成形复合材料格栅夹芯结构四点弯曲过程中的损伤状态,并结合渐进损伤有限元模型重点分析了面芯结合处和芯子壁板的变形、失效过程;Jiang等[9]利用ABAQUS有限元建模仿真和三点弯曲试验探究了面板为碳纤维复合材料、波纹芯子为铝合金的夹芯板的失效机理,发现该类型夹芯板的破坏过程分为弹性变形、面板断裂、延性破坏和芯子稳定变形4个阶段,据此设计的芯子水平加强筋能显著提高夹芯板的比吸能特性;Sun等[12]提出了一种基于弯曲强度和有限元连续损伤评估的设计方法,用于设计和分析几何参数对梯度波纹桁架夹芯结构承载能力和损伤分布的影响;Fan[13]对不同面板厚度的格栅夹芯板进行三点弯曲试验,揭示了复合材料格栅夹芯板的面芯脱粘和局部屈曲两种典型失效机制;吴启凡等[14]通过三点弯曲和四点弯曲试验研究了3种面板设置方式不同的复合材料格栅夹芯板的极限承载力和破坏形态,发现仅设置上面板的格栅结构具备延性破坏特征,其弯曲承载力和刚度均显著提高;王亚楠等[15]基于有限元仿真和试验分析了面板铺层角度、格栅厚度、格栅等效密度等因素对夹芯板弯曲刚度的影响。
以上文献多数采用有限元仿真、试验或二者结合的方法,较少采用理论计算的方法。原因是复合材料的各向异性、树脂基体的断裂脆性和损伤起始后的材料非线性使通过理论计算预测复合材料格栅/波纹夹芯板的弯曲峰值载荷、极限强度等重要设计参考值变得困难,而通过合理选择失效准则和刚度退化模式,有限元仿真却可以实现对各种边界、载荷条件下复合材料结构件失效模式和破坏过程的评估分析,辅之以少量试验验证后即可通过修改模型参数得到承载性能的变化规律,在时间允许的情况下降低试验成本。但正常工作状态下的复合材料格栅/波纹夹芯板仅发生线弹性范围内的小变形,需要评估的弯曲刚度不涉及强度破坏问题,在一定边界条件下按位移求解的三维弹性理论可实现对整个结构位移、应变和应力的分析。相比之下,格栅/波纹夹芯板细部结构复杂,采用有限元仿真计算弯曲刚度过程中的网格划分和尺寸敏感性分析、重复多次建模等问题反而会降低效率。在理论计算方面,Wei等[16]区分了全复合材料蜂窝夹心板在三点弯曲载荷下的芯子凹陷、剪切屈曲、剪切断裂、脱粘、胞元壁板凹陷和面板断裂等6种失效模式,利用建立的解析模型绘制了以结构参数为变量的三维失效机制图来预测三点弯曲刚度、破坏载荷和失效模式;邓忠民[17]提供了层压梁的弯曲刚度计算式,但该方法仅适用于发生柱状弯曲的层合板结构,而且也没有考虑横向剪切变形的影响;李华东等[18]基于高阶剪切理论建立了含有软质芯材复合材料格栅结构弯曲分析理论模型,求解了面板为正交对称铺层的四边简支格栅夹芯板的弯曲挠度,该模型与一阶剪切变形理论一样有5个未知位移函数变量,而且平衡微分方程组中的常系数的计算十分繁冗。
综合来看,全复合材料格栅、波纹夹芯板各有特点,目前还缺乏便于工程应用的理论计算方法来对比分析二者的弯曲刚度。本文先基于均质化理论将复合材料正交格栅、梯形波纹芯子等效为正交各向异性连续体,接着利用双变量高阶剪切精确板理论建立了横向均布载荷作用下复合材料夹芯板的弯曲分析模型,经有限元仿真验证模型有效性和准确性之后,计算并对比分析四边简支、对边简支和自由两种边界条件下结构参数、铺层参数对弯曲刚度的影响规律,旨在为复合材料格栅/波纹夹芯板的工程应用提供参考。
1 芯子等效弹性常数
图1 (a,b)分别为本文研究的复合材料正交格栅夹芯板和梯形波纹夹芯板的示意图,假设两种芯子均可等效为正交各向异性连续性弹性体,如图1(c)所示。
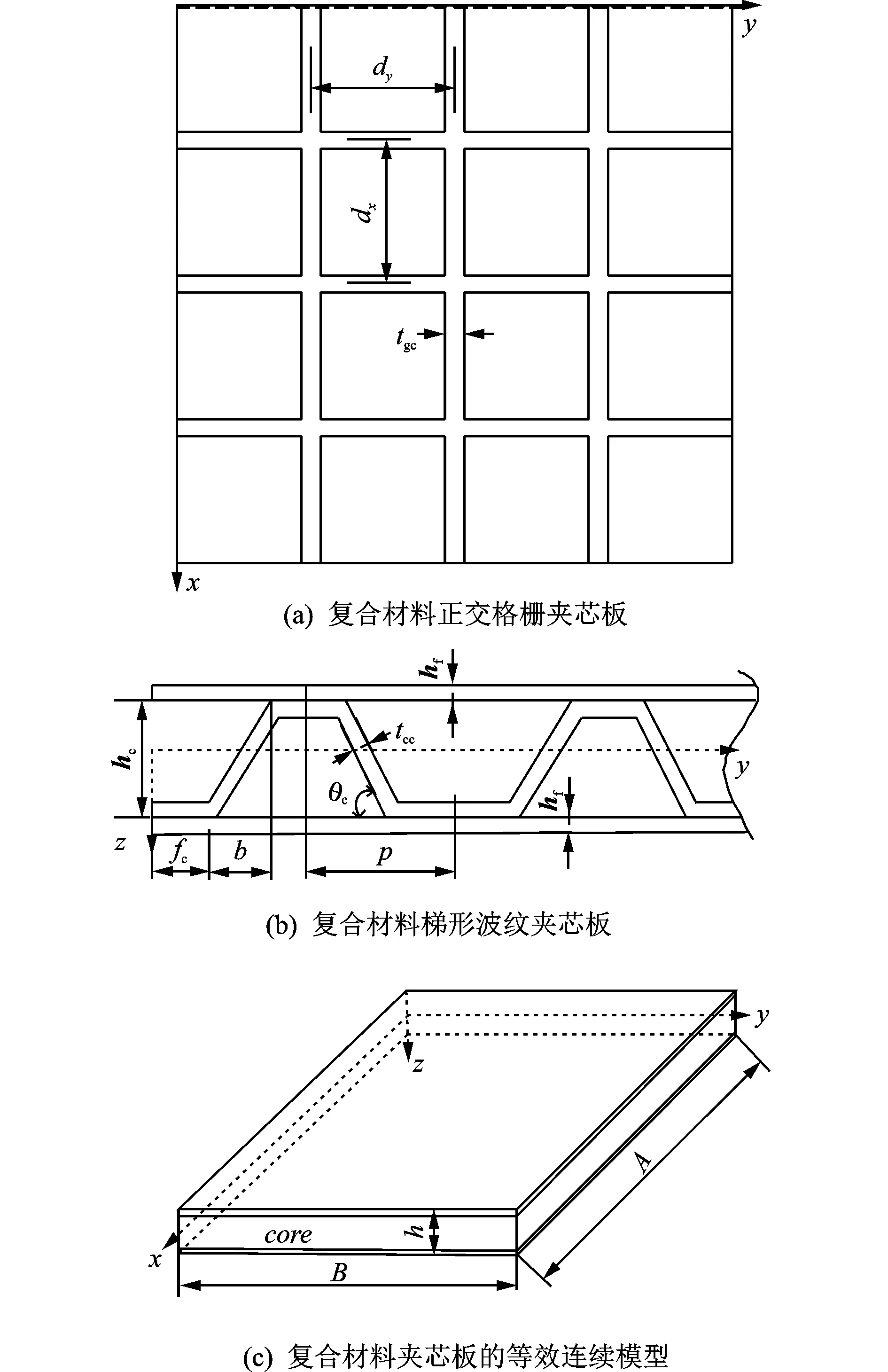
图1 复合材料格栅/波纹夹芯板及其等效连续模型
复合材料格栅、波纹芯子层合壁板的应变-内力关系为

(1)

(2)
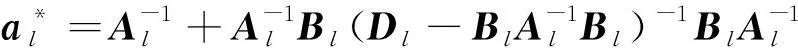
(3)

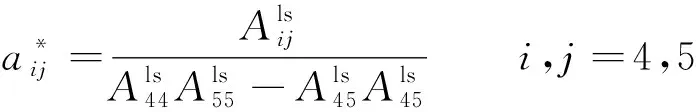
(4)
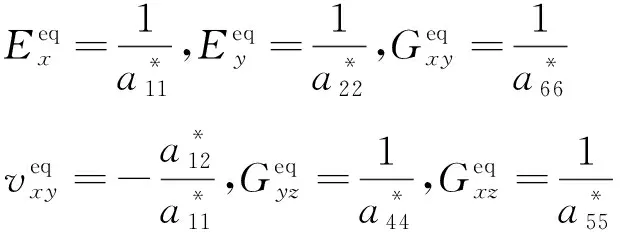
(5)


(6)

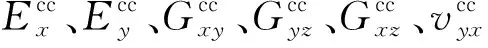
其中波纹芯子的变形柔度系数Cij及行列式的值C的表达式为
2 复合材料夹芯板弯曲分析理论模型
2.1 位移场
根据双变量高阶剪切变形精确板理论,复合材料夹芯板的位移场为[22]
式中:f(z) =-z/4+5z3/(3h2)为表征横向剪切变形的形函数;u0(x,y)、v0(x,y)为夹芯板中面上一点沿x、y方向上的位移;wb和ws分别为弯曲和剪切横向位移。根据线弹性范围内的变形几何关系,将式(9)代入后可得到
式(10)中物理量均由式(11)计算。
2.2 内力-应变关系
复合材料单层的本构关系为

(12)
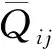
式中i=cc、gc。假设夹芯板承受的横向均布载荷q(x,y)=q,根据能量法,复合材料夹芯板整体应变能U和外力功V分别为

将式(12)代入式(15),化简后得到内力和应变的关系为
式(16)中各矩阵中的刚度系数定义为

i,j=1,2,4,5,6
(19)
2.3 平衡方程求解
由最小势能原理δ(U+V)=0及式(14)得到平衡方程为

(20)
对于四边简支的夹芯板,将满足其边界条件的位移函数wb、ws以及均布载荷q均采用双Fourier级数形式表示

(22)
式中:α=mπ/A,β=nπ/B,A、B分别为夹芯板x和y方向上的长度,m、n分别为对应的半波数;Wbmn、Wsmn和qmn为待定系数,qmn的计算式为
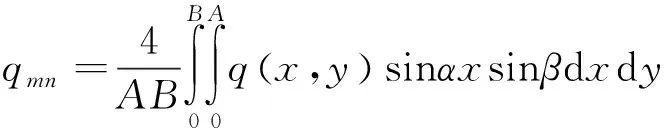
(23)
将式(22)代入式(21)后推导出
由式(24)可求得复合材料波纹夹芯板的弯曲挠度w。假设与y轴平行的一组对边为简支约束,另一组对边为自由状态,相应的位移函数及载荷q的展开式为
(25)
将式(25)代入式(21)平衡微分方程,有

(26)
自由边(y=0,B)的边界条件为

(27)
由式(26)可求出通解,再根据式(27)的边界条件,即可求出通解中的待定系数,求解过程均可在Matlab中实现。
3 模型有效性与参数分析
3.1 模型适用范围及验证

表1 碳纤维/环氧树脂复合材料单层的材料参数

表2 铺层方式及刚度系数的比值


(28)
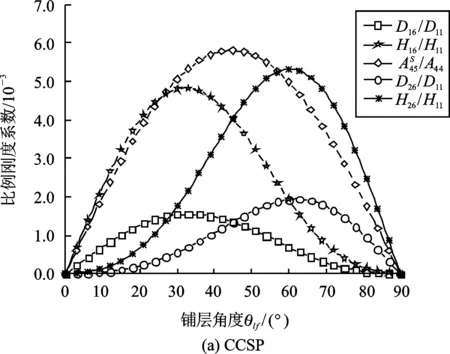
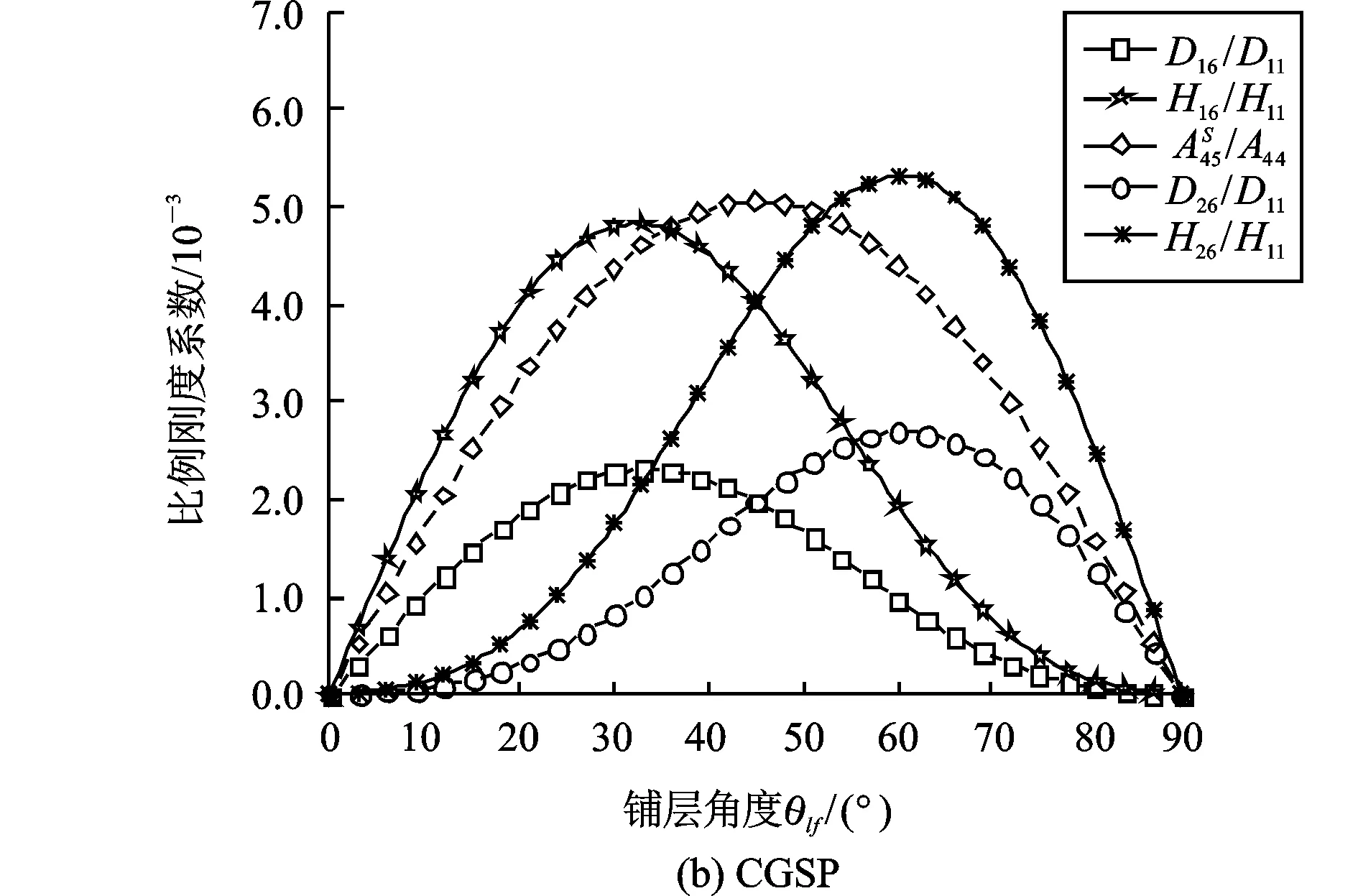
图2 算例CCSP和CGSP刚度系数的比值随铺层角度的变化
同时为了衡量复合材料波纹夹芯板结构的轻量化效益,定义比弯曲刚度Ki
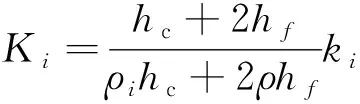
(29)
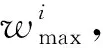

表3 CCSP和CGSP的弯曲刚度的理论解与有限元结果
3.2 铺层参数对弯曲特性的影响
保持算例结构参数不变,基于验证过的理论模型,计算0≤θlf=θlc≤90°,θlf=30°、0≤θlc≤90°和θlc=30°、0≤θlf≤90°三种铺层方式下两算例的弯曲刚度随铺层角度的变化规律,如图4所示。可发现SSSS边界条件下,CCSP和CGSP的弯曲刚度均在45°铺层取最大值,CCSP芯子壁板铺层角度θlc的变化对弯曲刚度的影响程度要大于面板铺层角度θlf,而CGSP正好相反,说明波纹芯子对弯曲刚度的增强效果更为明显;SSFF边界条件下,CCSP和CGSP的弯曲刚度随铺层角度增大而减小,在0°铺层取最大值;CCSP和CGSP在SSSS边界条件下的弯曲刚度远大于在SSFF边界条件下,说明增强边界条件可以提高弯曲刚度。
表4为两种边界条件下不同芯子铺层数的两算例的弯曲刚度、比弯曲刚度值。可看出随着芯子壁板铺层数增加,CCSP和CGSP的弯曲刚度显著提高,而比弯曲刚度却呈下降趋势,轻量化效益降低。

图3 复合材料格栅/波纹夹芯板的有限元仿真结果
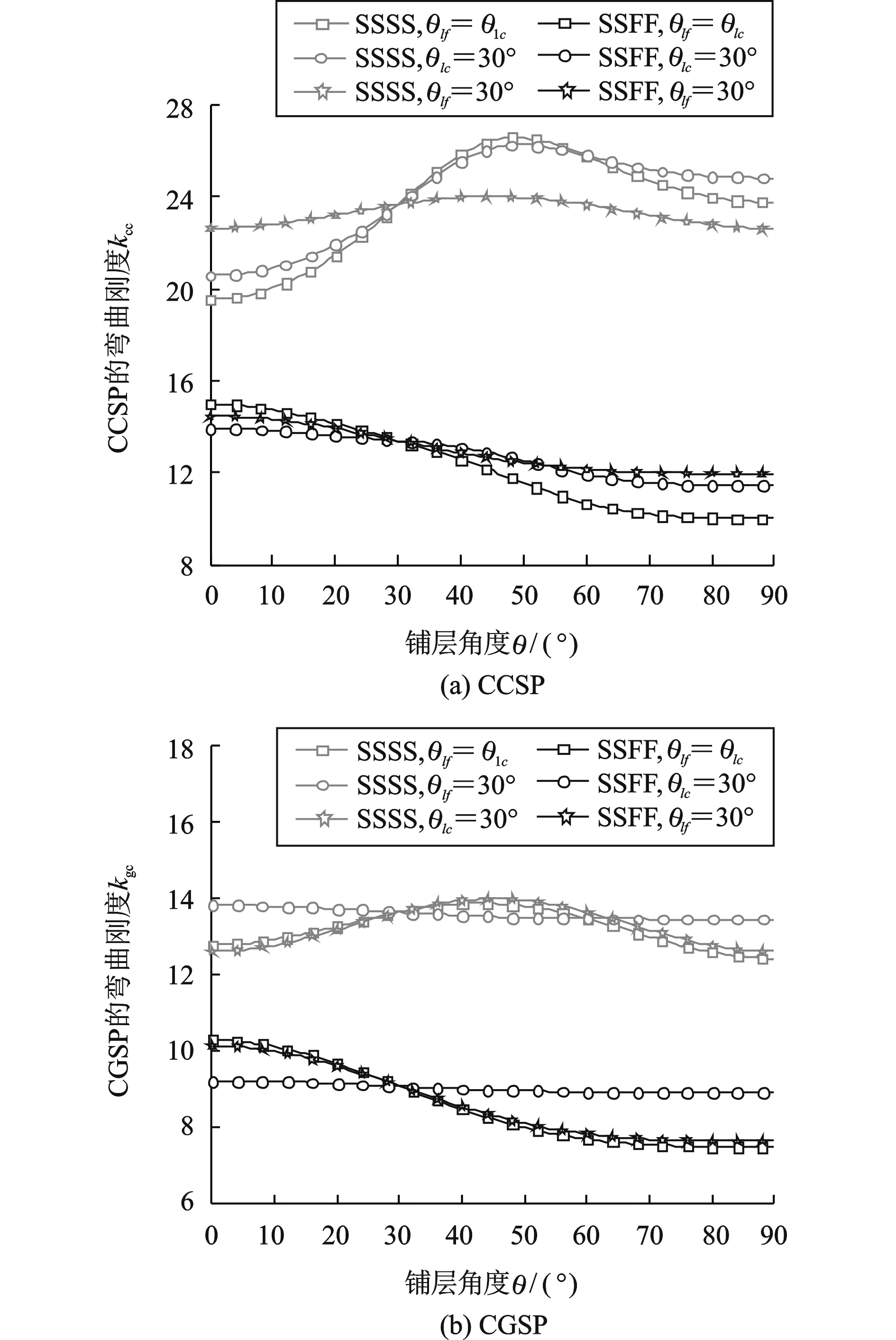
图4 铺层角度对复合材料夹芯板弯曲刚度的影响
保持芯子的铺层参数和除面板厚度以外的结构参数不变,绘制两个算例的ki和Ki随面板铺层数nf的变化规律,如图5所示。可看出两种边界条件下,CCSP和CGSP的弯曲刚度和比弯曲刚度均随面板铺层数的增大而非线性增大,CCSP的比弯曲刚度一直大于CGSP。

表4 芯子壁板铺层数对弯曲特性的影响
3.3 结构参数对弯曲特性的影响
保持CCSP面板的所有参数和波纹芯子的铺层参数不变,基于精确板理论模型分析,分析复合材料波纹芯子的3个结构参数hc,fc=kb和θc对弯曲刚度和比弯曲刚度的影响,计算结果如图6所示。
由图6可知, 增大芯子高度能显著提高CCSP的弯曲刚度和比弯曲刚度;波纹水平段fc与倾斜段水平距离b的比值在0.5左右时,弯曲刚度取最小值;随着fc与b比值的增大,CCSP的比弯曲刚度显著增大;波纹倾角θc从15°增大到90°时,CCSP的弯曲刚度和比弯曲刚度均呈先减小后增大的趋势。
类似地,保持CGSP的其他参数不变,绘制其弯曲刚度、比弯曲刚度随格栅高度hc和格栅间距dx(dy=dx)的变化曲线,如图7所示。

图7 结构参数对复合材料格栅夹芯板弯曲特性的影响
CGSP的弯曲刚度和比弯曲刚度随芯子高度hc的增大而显著增大;CGSP的弯曲刚度随格栅间距dx增大而减小,当格栅间距dx与板宽A的比值大于0.5时,格栅间距增大对弯曲刚度的影响程度较小,CGSP比弯曲刚度随格栅间距的变化趋势正好相反。
4 结论
基于双变量高阶剪切理论建立了全复合材料正交格栅/梯形波纹夹芯板弯曲分析模型,计算了这两种夹芯板在四边简支、对边简支两种边界条件下的弯曲刚度,并通过有限元仿真进行了验证,还对比分析了铺层参数和结构参数对两种夹芯板弯曲刚度、比弯曲刚度的影响规律。
(1) 四边简支复合材料格栅和波纹夹芯板的弯曲刚度均在45°铺层取最大值,而对边简支和自由条件下二者在0°铺层取最大值;波纹芯子对弯曲刚度的增强效果大于格栅芯子,复合材料梯形波纹夹芯板的轻量化效益更显著。
(2) 随着芯子铺层数nc增大,两种夹芯板的弯曲刚度增大,比弯曲刚度却减小,轻量化效益下降;随着面板铺层数nf和芯子高度hc的增大,两种夹芯板的弯曲刚度和比弯曲刚度均增大。
(3) 复合材料梯形波纹夹芯板的波纹水平段fc与倾斜段水平距离b的比值在0.5左右时,弯曲刚度取最小值;随着fc与b比值的增大,比弯曲刚度显著增大;波纹倾角θc从15°增大到90°时,弯曲刚度和比弯曲刚度均呈先减小后增大的趋势。
(4) 复合材料格栅夹芯板的弯曲刚度随格栅间距dx增大而减小,当格栅间距dx与板宽A的比值大于0.5时,格栅间距增大对弯曲刚度的影响程度较小,比弯曲刚度的随格栅间距的变化趋势正好相反。
