混合动力汽车自适应等效油耗最低能量管理策略

胡建军，杨 颖，邹玲菠，彭 桃

(重庆大学 汽车工程学院，重庆 400044)

近年来，随着世界上汽车总量不断攀升，能源与环境成为了不可忽视的问题[1]。插电式混合动力汽车以电能和燃油作为能量源，能够有效提升汽车燃油经济性，同时降低尾气排放，非常具有研究意义[2]。能量管理策略是插电式混合动力汽车的核心技术之一，决定了动力源之间的动力分配关系，对插电式混合动力汽车的动力性、燃油经济性、排放等都有重大影响。在目前的研究中，插电式混合动力汽车能量管理策略主要被分成为两大类[3-4]：基于规则的控制策略和基于优化的控制策略。

基于规则的控制策略又分为基于确定规则与基于模糊规则的控制策略。基于确定规则的控制策略[5-7]通过设立车速、电池荷电状态(SOC，公式和图表中用Sbat表示)、需求转矩、功率等逻辑门限值，控制汽车进入不同的工作模式，从而提升汽车的燃油经济性。这类方法简单直观，实用性强，但对工况的变化非常敏感，确定的逻辑门限值不能良好地适应各种不同工况。为此，有学者提出基于模糊规则的控制策略[8-11]。程飞等[11]采用基于模糊规则的控制策略，通过对SOC、ΔSOC、K值(需求转矩与当前转速下发动机最大转矩的比值)模糊化，制定相应的模糊规则，控制电机和发动机高效工作。基于模糊规则相比于基于确定规则的控制策略在一定程度上减少了对工况的依赖性，可实现非线性控制，鲁棒性好。但它也是依靠专家经验人为地根据发动机和电机工作特性进行经验性控制与调节，插电式混合动力汽车的燃油经济性仍有提升空间。

基于优化的控制策略包括基于全局优化的控制策略与基于瞬时优化的控制策略。基于全局优化的控制策略[12-15]主要包括基于动态规划(dynamic programming, DP)的控制策略、基于庞特里亚金最值原理(Pontryagin’s minimum principle, PMP)的控制策略。段骏华等[12]采用改进型DP控制策略，仿真结果表明采用该改进型DP控制策略可有效降低油耗。Kim等[15]用庞特里亚金最值原理获得全局最优解，其燃油经济性与DP十分接近。基于全局优化的控制策略可使汽车达到最佳燃油经济性，但需预先知道未来行驶工况，同时数值计算量巨大，无法适用于插电式混合动力汽车的实时控制。基于瞬时优化的控制策略[16-22]主要包括基于模型预测控制 (model predictive control, MPC) 的控制策略和基于等效油耗最低的控制策略(equivalent consumption minimization strategy, ECMS)。Zhao等[16]使用基于模型预测的控制策略，将整个驾驶循环燃油经济性的全局最优控制转化成预测区域内的局部优化控制，以油耗最小化为目标进行滚动优化。Paganelli等[18]较早提出了ECMS，科学地将电量消耗等效为燃油消耗，实时选择综合油耗最低的工作点。欧阳等[20]采用ECMS通过BP神经网络识别行驶路况，优化不同行驶路况的能量流动控制。Zhang等[21]采用改进的ECMS结合模糊PI算法调整等效因子，保证电池电量较为恒定，使得混合动力汽车的燃油经济性进一步提高。

ECMS无需专家经验，控制效果优于基于规则的管理策略；无需预知未来工况，工况适应性好；计算量远小于基于全局优化的控制策略，可实现实时控制和瞬时等效油耗最低，拥有着良好的应用前景。该类方法通过等效因子将电能消耗等效为燃油消耗，因此制定等效因子是其核心，也是影响燃油经济性表现的关键因素。普通混合动力汽车只能通过发动机消耗燃油补充电能，故而电能消耗可合理等效为燃油消耗，文献[18]中制定等效因子的方法被广泛采用。但插电式混合动力汽车可通过电网给电池充电，目前其油电等效因子并没有统一的制定方法。

笔者通过动态规划算法，分析了不同典型工况、不同行驶距离下的最优SOC下降轨迹，并得到了最优SOC轨迹和行驶距离的一般规律；结合最优SOC轨迹和行驶距离的一般规律，建立了单次充电行驶里程的概念并制定了一种新型的等效因子制定方法，进而在传统ECMS的基础上，提出了一种可实时控制的自适应等效油耗最低能量管理策略(adaptive equivalent consumption minimization strategy, AECMS)。

1 并联插电式混合动力汽车建模

基于Matlab建模仿真平台，对某并联插电式混合动力汽车(PHEV)展开研究。其整车构型如图1所示，图中C1为离合器，MG为ISG电机，AT为4挡自动变速器。

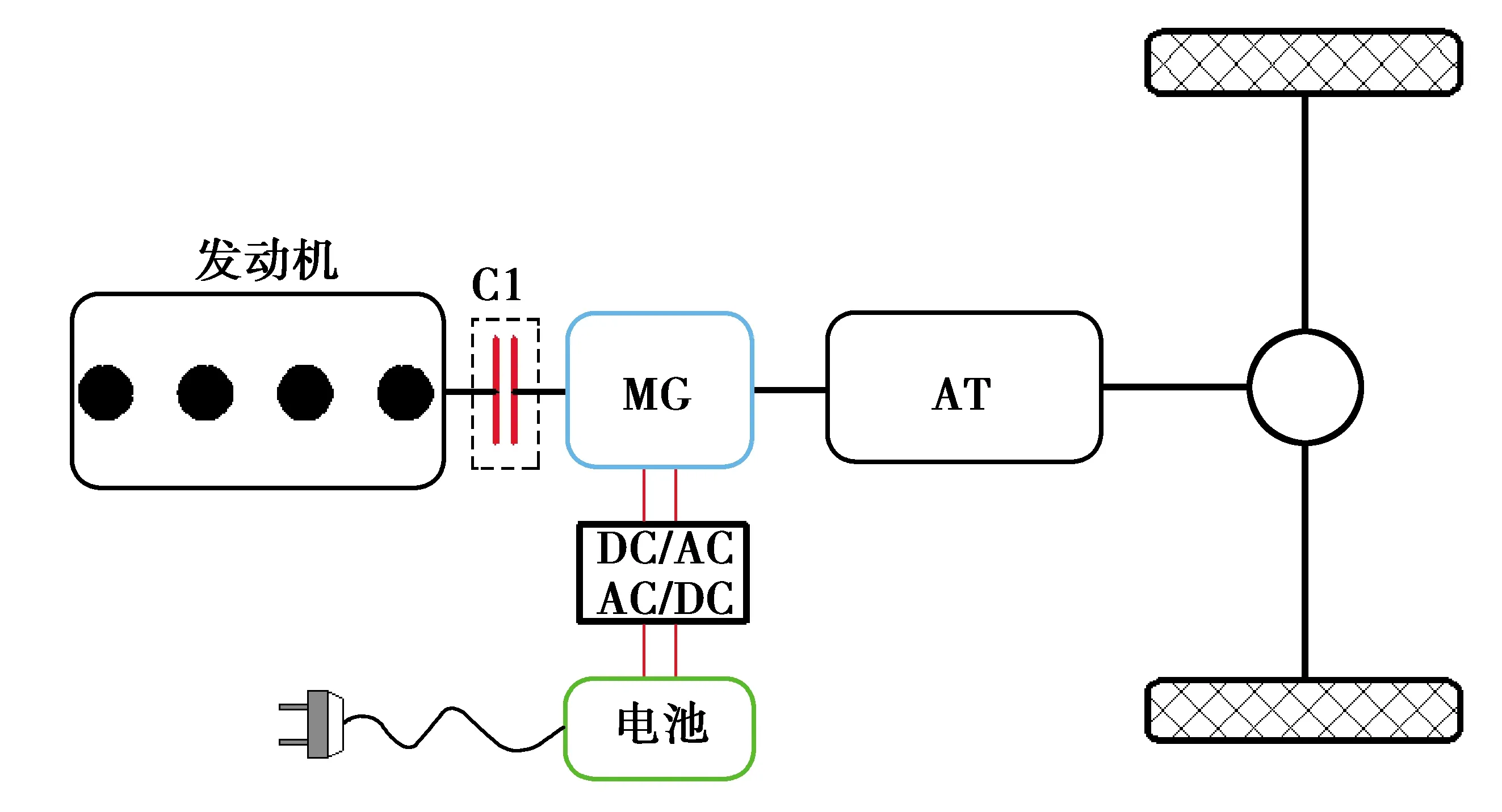
图1 某并联插电式混合动力汽车构型Fig. 1 Configuration of a parallel PHEV

整车参数如表1所示，发动机、电机、电池等部件数值模型数据均为台架测试数据。该插电式混合动力汽车共有5种工作模式，分别为纯电动模式(P_+EV)、发动机单独驱动模式(P_engine)、混合驱动模式(P_engine+MG)、行车充电模式(P_engine-MG)、制动回收模式(P_-EV)。各工作模式下各部件的工作状态如表2所示。

表1 汽车参数

表2 各工作模式下各部件的工作状态

1.1 发动机

通过数值建模得到发动机燃油消耗率的数值模型如图2所示。通过发动机的工作转速和转矩可插值得到发动机的燃油消耗率。

图2 发动机燃油消耗率map图Fig. 2 Engine fuel consumption rate map

1.2 电机

电机模型也通过数值模型建立，电机效率的数值模型如图3所示。

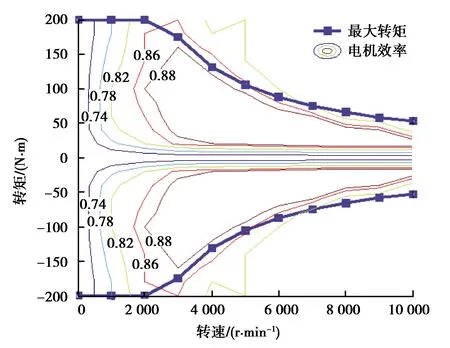
图3 电机效率map图Fig. 3 Motor efficiency map

电机在转矩为正时处于驱动状态，转矩为负时处于发电状态。驱动状态下的电机功率由式(1)计算，发电状态下由式(2)计算：

Pm_dis=nmTm/ηm_dis，

(1)

Pm_chg=nmTmηm_chg。

(2)

式中：nm和Tm分别代表电机的转速和转矩；Pm_dis和ηm_dis分别代表电机驱动状态下的功率和效率；Pm_chg和ηm_chg分别代表电机发电状态下的功率和效率。

1.3 电池

选用电池内阻模型[22]，电池功率由式(3)计算：

(3)

式中：Pbat为电池功率；Voc为电池开路电压；Ibat为电池电流；Rbat为电池内阻。Voc和Rbat均与电池电量状态(SOC)有关，其数值模型如图4中(a)(b)所示。

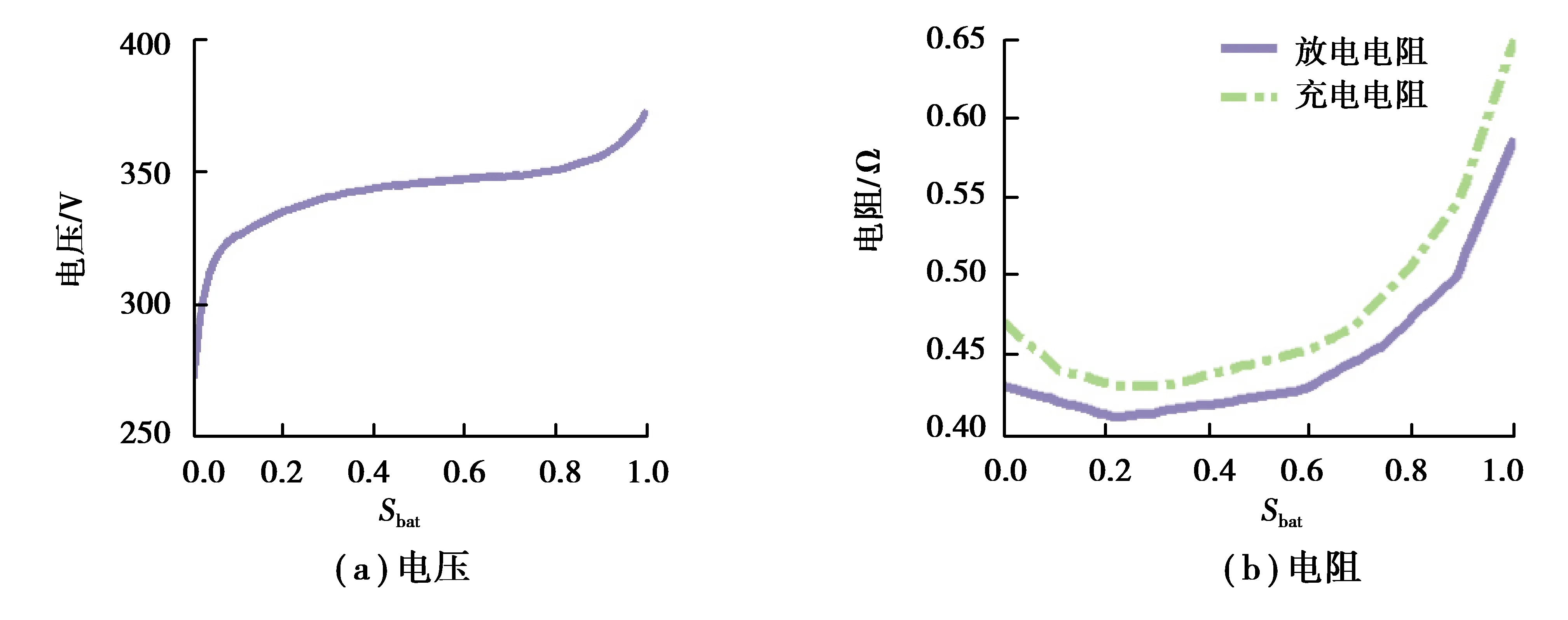
图4 电池模型Fig. 4 Battery model

对式(3)求解得到电池电流：

(4)

电池SOC由式(5)计算得到：

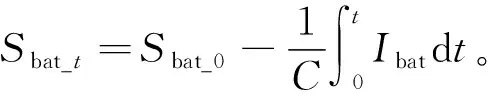
(5)

式中：Sbat_t为电池经过时间t后的SOC；Sbat_0为电池起始SOC；C为电池容量；t为电池充放电的时间。

2 控制策略设计

插电式混合动力汽车的能量由电能和燃油共同提供，各能量源之间的关系如图5所示。

图5 混合动力系统能量流动图Fig. 5 Energy flow diagram of hybrid power system

插电式混合动力汽车的各能量源的关系如式(6)所示：

Eele+Efuel=Ereq。

(6)

式中：Eele为电能，Efuel为燃油能量，Ereq为需求能量。

由式(6)可知，插电式混合动力汽车的需求能量由电能和燃油能量组成。在各个时刻，当需求能量Ereq确定时，可以分配不同的Eele和Efuel以达到驾驶员的动力需求。当Eele为正时电机消耗电池电能，当Eele为负时通过发动机发电或者制动回收补充电池电能。基于全局优化的控制策略可以在各约束条件下，获得各时刻方程的最优解序列，通过最优分配电能和燃油能量，使各时刻燃油消耗量之和最小，是理论上的最优控制策略。SOC轨迹是电池电能消耗的表现形式，从SOC轨迹可以得到各时刻电能的使用情况，继而可得到各个时刻电能和燃油能量的分配方式。

如图6(a)所示，当采用最优控制策略时，可通过最优分配电能和燃油能量，使汽车达到最低燃油消耗，此SOC下降轨迹便是最优SOC下降轨迹。从另一个角度来说，如图6(b)所示，如果已知某段行程中最优SOC下降轨迹，就可以实时分配电能和燃油能量，使实际SOC沿最优SOC下降轨迹变化。此时电能和燃油能量的分配方式等同于最优控制策略，汽车可达到最低燃油消耗。可以得到如下推论：如果提前规划出某段行程的最优SOC下降轨迹，就可使汽车在这段行程中达到最低燃油消耗。

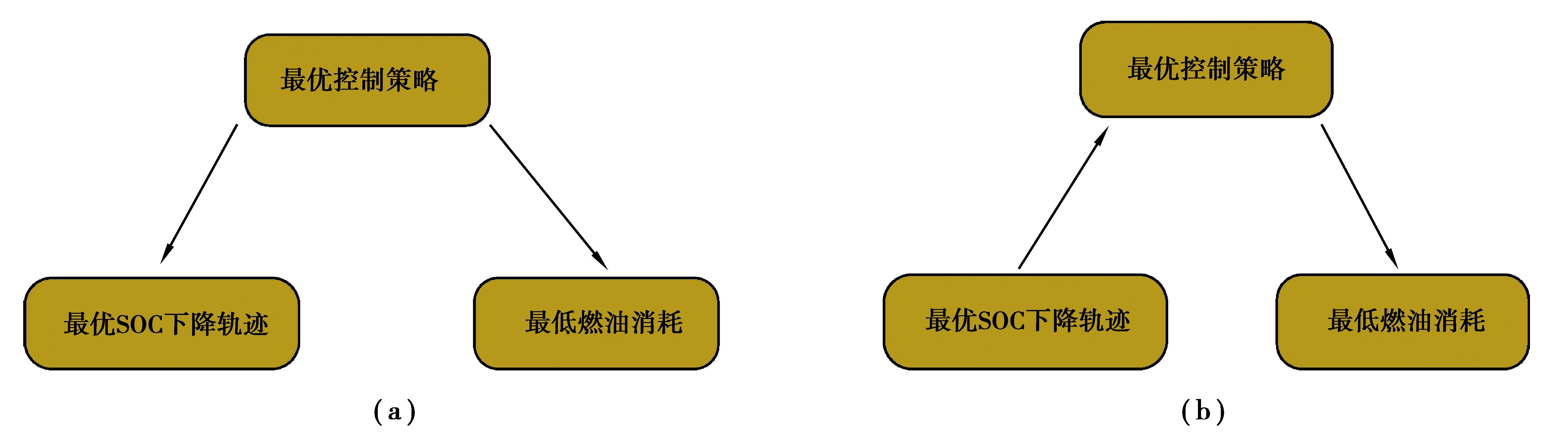
图6 能量管理策略逻辑推理图Fig. 6 Logic reasoning diagram of energy management strategy

2.1 DP控制策略

动态规划算法(DP)的原理是把一个连续的过程离散化，从全局的角度得出一个最优解。DP控制策略是一种基于全局优化的控制策略，通过DP控制策略可以使汽车在某段行程中燃油消耗最低。笔者基于DP控制策略仿真分析不同行驶距离、不同工况条件下的最优SOC下降轨迹，在此基础上探讨SOC的变化规律。

2.1.1 模型搭建及求解

将电池的荷电状态SOC定义为状态变量，将发动机的转矩Te、自动变速器挡位ig、工作模式m定义为控制变量。当系统状态从k阶段转移到k+1阶段时，则系统的状态转移方程为：

Sbat(k+1)=Sbat(k)-ΔSbat(k)。

(7)

将发动机转矩Te离散化，在状态转移的过程中，当各控制变量取不同值时，将产生不同的燃油消耗及电量消耗，这就是递推过程中每一步产生的成本。将每一步的成本叠加就得到了整个系统的成本函数。成本函数由式(8)描述：

(8)

式中：Δffuel(k)为第k阶段燃油消耗；fSOC(k)为第k阶段惩罚项；F1(k)为第k阶段的成本；N为总的阶段数；J1_min为整个过程的最小成本。

惩罚函数由式(9)描述：

(9)

式中Sbat_low为电池理想工作区荷电状态下限值。

在求解过程中，将每个阶段的状态变量和控制变量离散化后，并把整个测试工况按单位时间(1 s)进行离散，采用插值的方式逐步求解[12]。各控制变量与状态变量离散化程度如表3所示。

表3 各变量离散化程度

2.1.2 DP控制策略结果分析

为探究行驶距离、工况等重要因素对燃油经济性的影响，采用4种不同行驶距离以及8种典型工况进行离线仿真，包括代表城市工况的UNIF01、WVUSUB、SC03，代表高速工况的WVUINTER、REP05和代表综合工况的NEDC、WLTP、LA92。为减少对电池的损害，设定SOC初始值为0.9，SOC下限值为0.3[23]。不同循环工况、不同行驶距离下最优SOC下降轨迹如图7所示，所有SOC最终都下降到0.3附近，说明DP控制策略充分利用了电池电能，并通过惩罚函数限制电池电量不下降到过低的水平。可以观察到即使工况不同、行驶距离不同，最优SOC都大致随行驶距离沿直线下降。

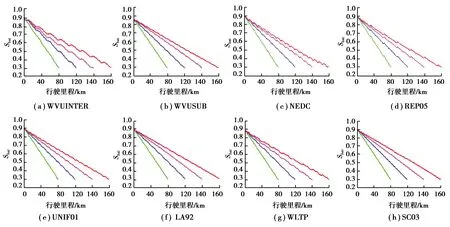
图7 不同典型工况、不同行驶距离下SOC变化曲线Fig. 7 SOC change curve under different typical working conditions and different driving distances

2.2 自适应等效油耗最低能量管理策略

如前文所述，传统ECMS具备良好的应用前景。ECMS最初被提出是为了改善普通混合动力汽车燃油经济性，由于普通混合动力汽车电池电能几乎全部来源于燃油，所以可计算出合理的等效因子将电能消耗等效为燃油消耗。插电式混合动力汽车的电池电能来源为燃油及电网，目前其等效因子没有统一的制定方法。为保证充分利用电池电能，ECMS对于插电式混合动力汽车时的控制方法如下：当电量充足时，汽车仅以纯电动模式运行，电池处于电量消耗(CD)阶段；当SOC下降到其限制值时，汽车可使用所有工作模式，电池处于电量保持(CS)阶段。ECMS可使汽车在CD阶段瞬时电量消耗最低，在CS阶段瞬时等效燃油消耗最低。这种方式的控制下，SOC先迅速下降，后保持在其限制值附近。该控制策略下的SOC轨迹与DP控制策略下的最优SOC下降轨迹存在较大差异，且油耗明显高于DP控制策略。故笔者在ECMS的基础上，提出了一种改进的控制策略——自适应等效油耗最低能量管理策略(AECMS)。

2.2.1 模型搭建

从前文推论可以看出，提前规划出某段行程中的最优SOC下降轨迹，可使汽车燃油消耗最低。而汽车实际工作过程中，路况复杂且受外界因素影响而随时改变，所以不可能提前规划出最优SOC下降轨迹。DP控制策略的仿真结果显示，最优SOC轨迹都大致随里程沿直线下降，最终下降到电池理想工作区荷电状态范围下限值。根据DP控制策略仿真结果，可以用一条直线作为SOC理论参考轨迹(图8)，代替最优SOC下降轨迹。

图8 SOC理论参考轨迹Fig. 8 SOC theoretical reference trajectory

图8中：纵轴为SOC，横轴为行驶距离，Sbat_initial为初始SOC，L为单次充电行驶里程。以纯电动续驶里程标称为60 km的某插电式混合动力汽车为例，若用户习惯于每行驶200 km充电一次，则该车的单次充电行驶里程为200 km，故单次充电行驶里程不同于纯电动续驶里程。用户可根据自己的用车习惯以及充电条件，自行设定单次充电行驶里程。

通过SOC理论轨迹，整段行程中行驶距离X处的SOC理论参考值Sbat_ref可由方程(10)得到：

(10)

AECMS定义在某一瞬时工况下将电机的能量消耗折算成发动机的燃油消耗，即等效油耗，引入等效因子建立每一阶段的综合油耗成本函数。AECMS的成本函数可由式(11)描述：

(11)

式中：Δffuel(k)为第k阶段燃油消耗；λ为等效因子；ΔSbat(k)为第k阶段的电池SOC变化量；F2(k)为第k阶段的成本；J2_min为各阶段最低成本之和。

利用PI算法实时调整更新等效因子λ，使SOC实际轨迹能够大致跟随理论参考轨迹。λ由式(12)(13)描述：

et=Sbat_ref-Sbat_X，

(12)

(13)

式中：Sbat_X为行驶X距离后SOC的实际值，Kp为比例系数，Ki为积分系数。

2.2.2 约束条件

SOC、发动机转矩Te、发动机转速ωe、电机转矩Tm、电机转速ωm、电池输出功率Pbat_dis、电池充电功率Pbat_chg需要同时服从式(14)的约束：

(14)

式中：Sbat_min为SOC最小值0；Sbat_max为SOC最大值1；ωe_min和ωe_max为发动机最低和最高转速；Te_min和Te_max为发动机在转速为ωe(k)时的最小和最大转矩；ωm_min和ωm_max为电机最低和最高转速；Tm_min和Tm_max为电机在转速为ωm(k)时的最小和最大转矩；Pbat_chg_max和Pbat_dis_max为电池最大充电和放电功率。

2.2.3 求解过程

AECMS是一种基于瞬时优化的控制策略，通过求解单位时间(1 s)的最低综合油耗，可实现实时控制。AECMS的求解如图9所示。

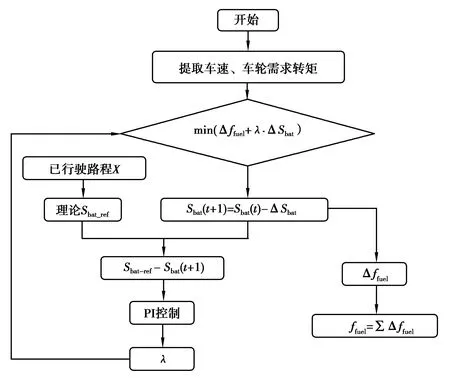
图9 AECMS求解过程Fig. 9 AECMS solution process

3 结果分析

为充分对比ECMS、DP、AECMS 3种控制策略下汽车的燃油消耗、SOC曲线轨迹、发动机与电机工作点分布，以不同单次充电行驶里程及不同典型工况作为仿真条件。所采用的典型工况如图10所示，包括代表综合工况的NEDC、WLTP，代表城市工况的UDDS以及代表高速工况的HWFET。

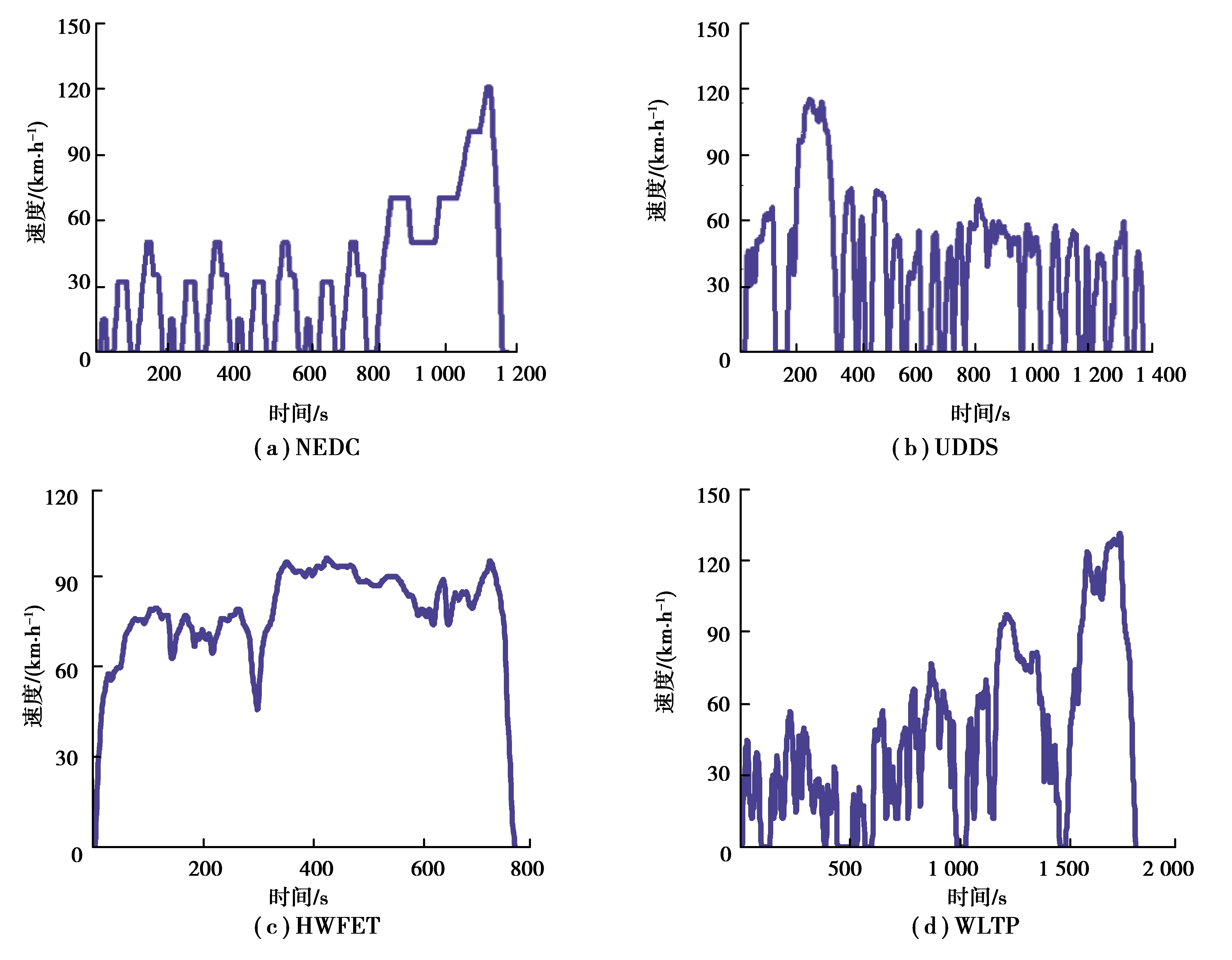
图10 各典型工况Fig. 10 Typical working conditions

3.1 CD模式仿真结果及分析

表4～7为初始SOC为0.9时3种控制策略的燃油消耗结果对比。在不同工况、不同单次充电行驶里程的情况下，AECMS相对于传统ECMS能节省燃油3.50%～8.71%，相对于DP控制策略多消耗燃油2.27%～6.70%。图11为NEDC工况、160 km单次充电行驶距离条件下的仿真结果，其中(a)为SOC随行驶距离变化曲线；(b)(c)(d)为3种控制策略下的发动机工作点；(e)(f)(g)为3种控制策略下的电机工作点。AECMS可适应各种工况及单次充电行驶里程，通过控制SOC实际轨迹随行驶距离沿直线下降，其对电能与燃油能量的分配方式与DP控制策略相似，从而有效降低燃油消耗。

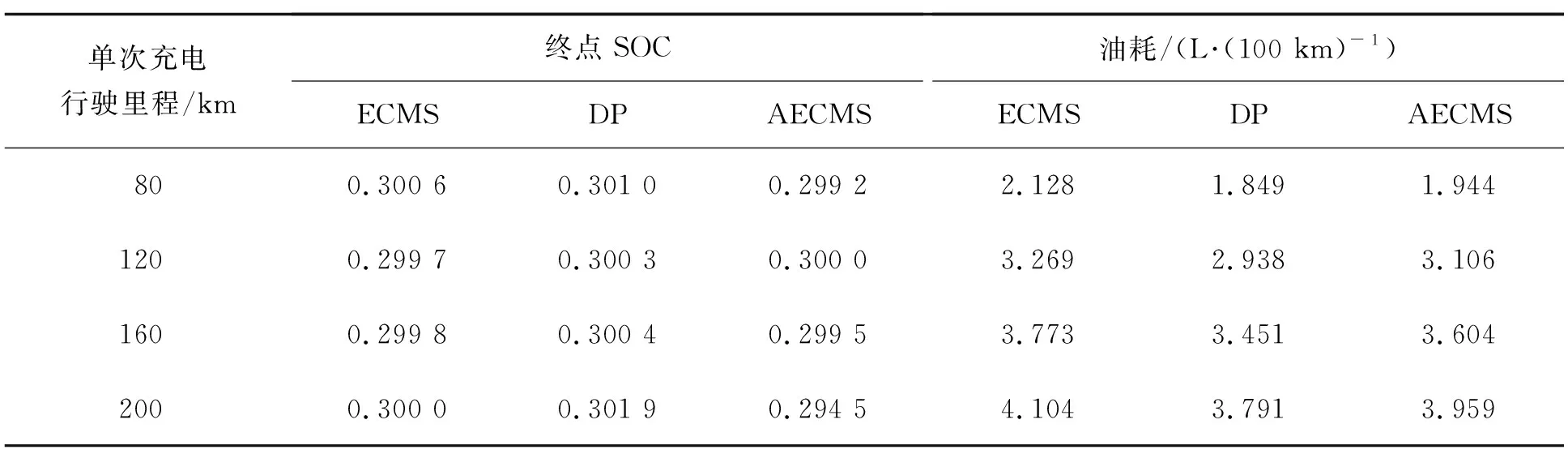
表4 NEDC工况下3种控制策略燃油消耗结果

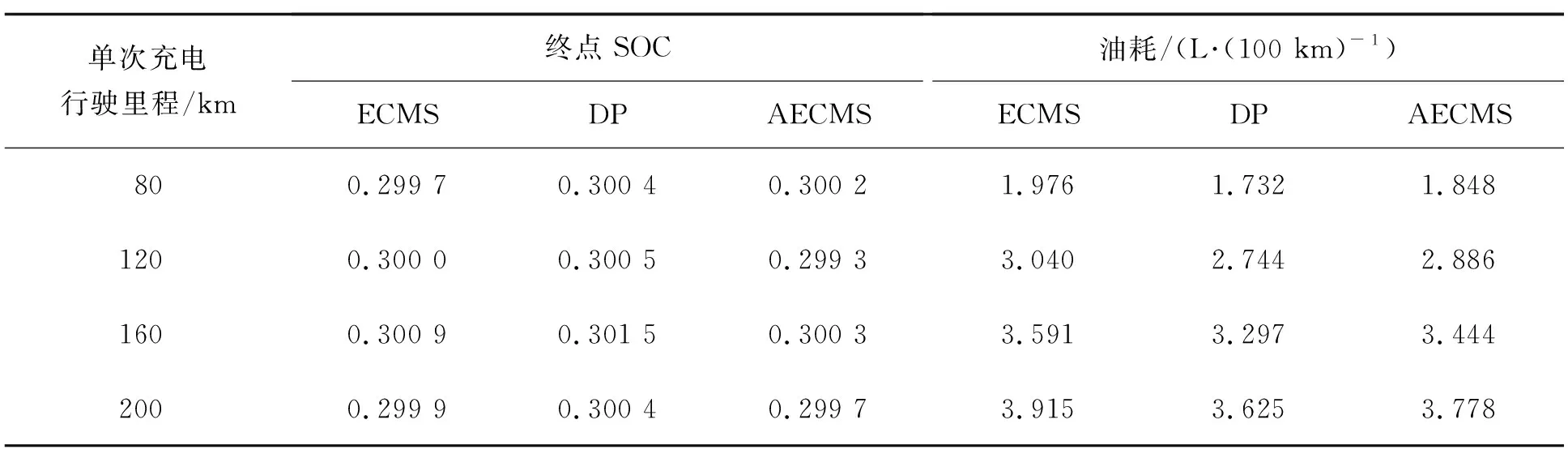
表5 UDDS工况下3种控制策略燃油消耗结果

表6 HWFET工况下3种控制策略燃油消耗结果

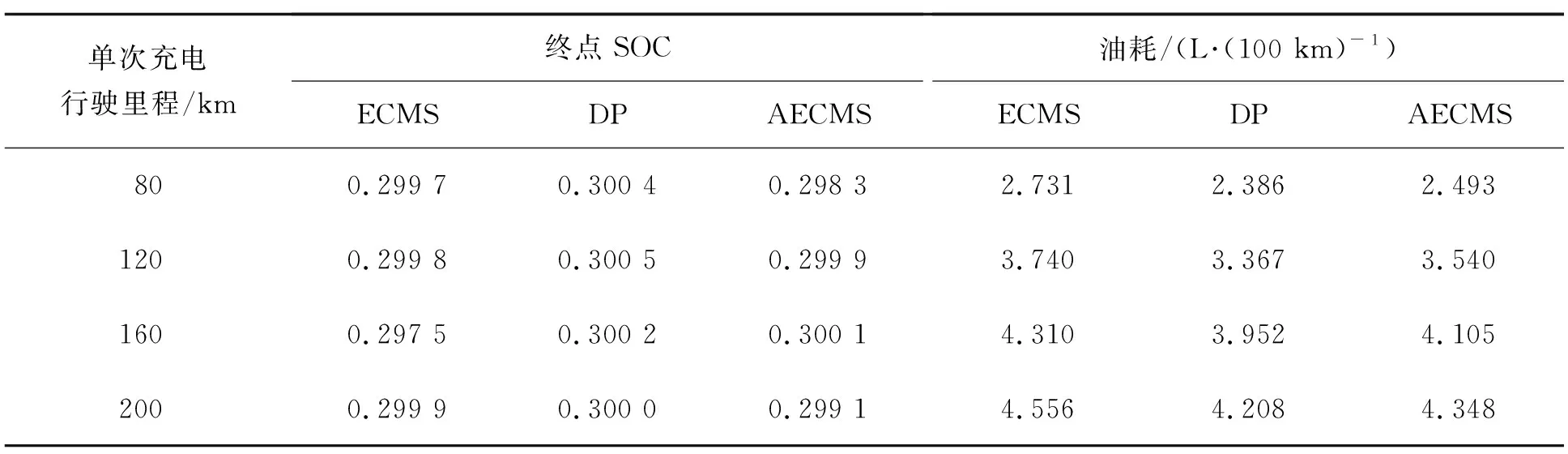
表7 WLTP工况下3种控制策略能量消耗结果

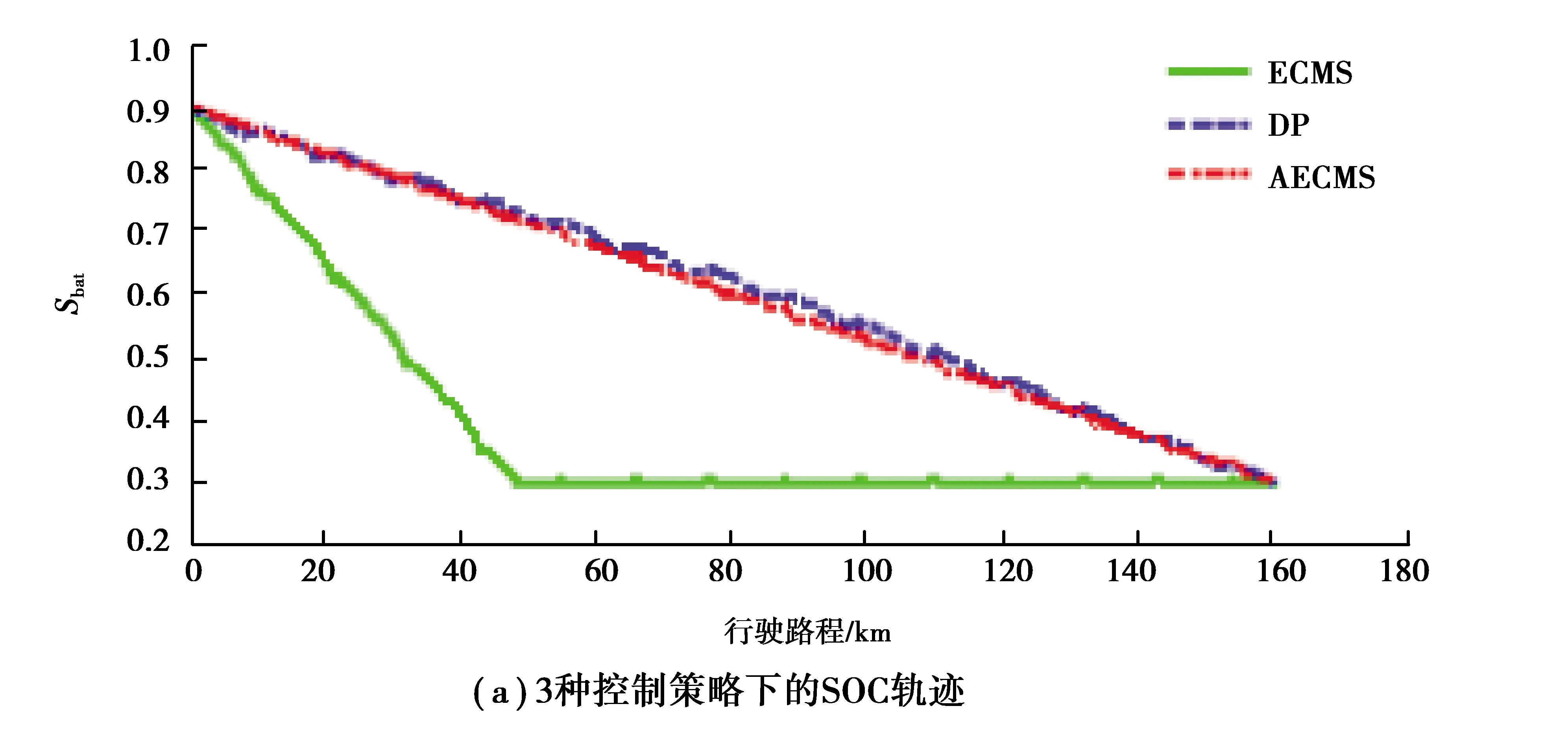
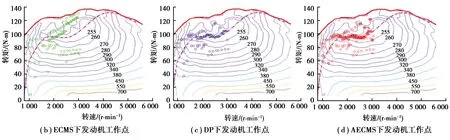
图11 CD模式下3种控制策略的仿真结果对比Fig. 11 Comparison of simulation results of three control strategies in CD mode

3.2 CS模式仿真结果及分析

结合实际情况，部分用户因充电条件受限而极少通过电网为汽车充电，因此插电式混合动力汽车在电量维持(CS)模式下的油耗表现同样十分重要。表8为初始SOC为0.3时3种控制策略的燃油消耗结果对比。在不同工况、不同单次充电行驶里程的情况下，AECMS相对于传统ECMS能节省燃油1.11%～2.46%，相对于DP控制策略多消耗燃油0.78%～2.65%。图12为NEDC工况下的仿真结果，其中(a)为SOC随行驶距离变化曲线；(b)(c)(d)为3种控制策略下的发动机工作点；(e)(f)(g)为3种控制策略下的电机工作点。AECMS控制下SOC始终维持在0.3附近，发动机工作点主要分布在最佳燃油经济线附近。AECMS可实时改变等效因子，使发动机更好地工作于高效区。

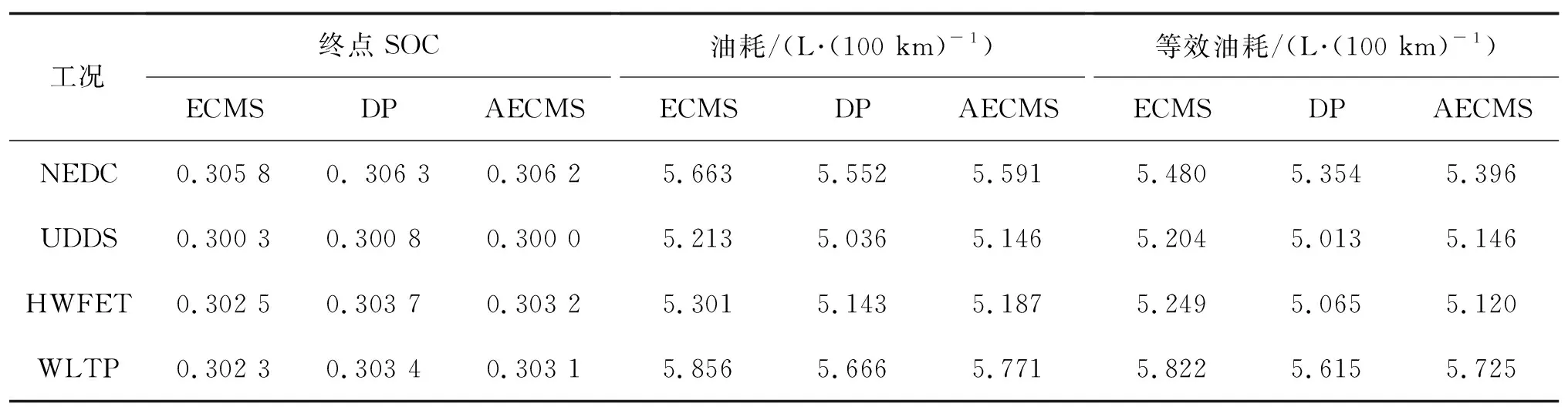
表8 NEDC工况下3种控制策略的燃油消耗

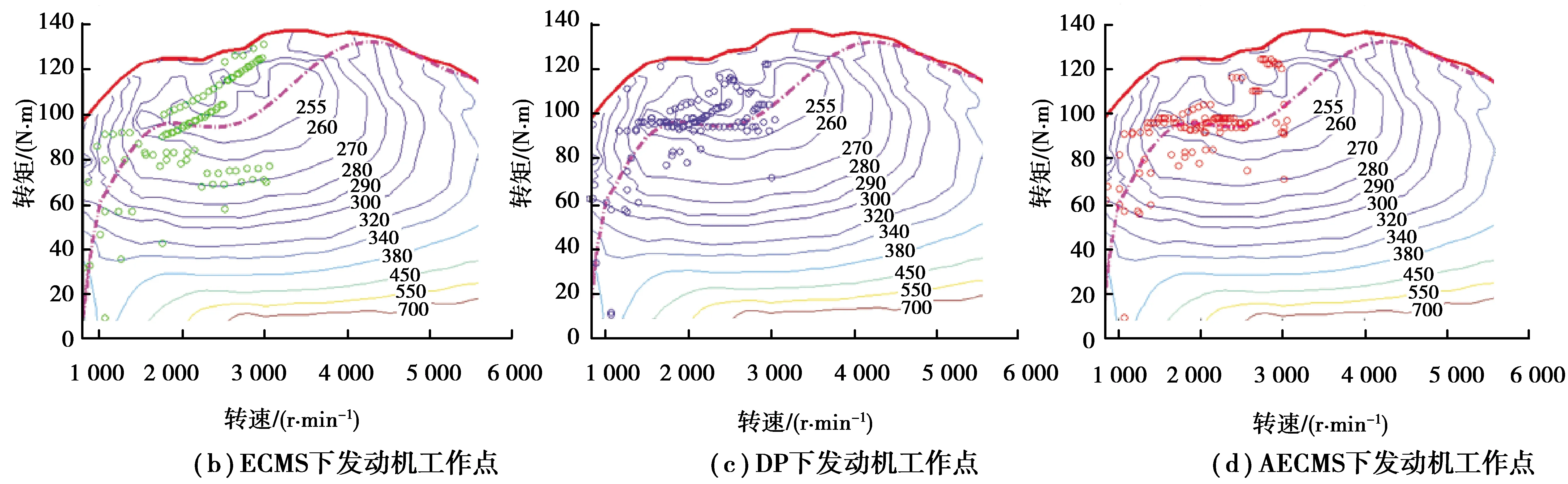
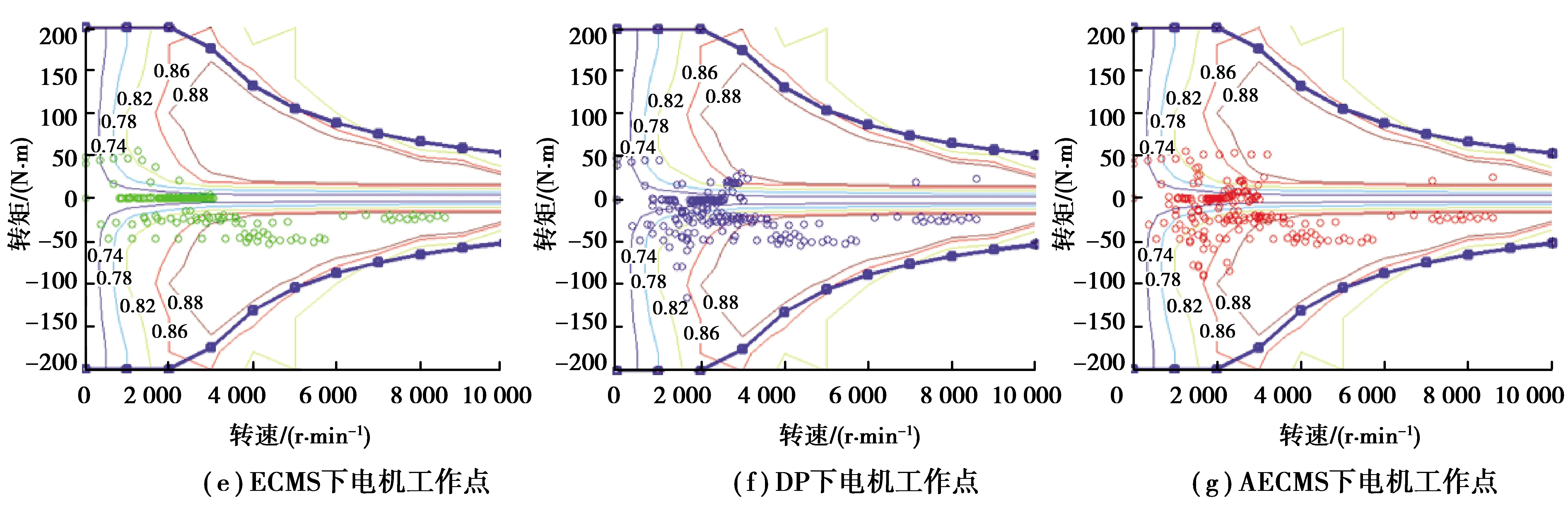
图12 CS模式下3种控制策略的仿真结果对比Fig. 12 Comparison of simulation results of three control strategies in CS mode

4 结 语

为了提高混合动力电动汽车的燃油经济性，采用DP算法对不同典型工况和不同行驶距离下的最优SOC轨迹进行了仿真分析，得到了最优轨迹与行驶距离的一般规律。在此基础上，建立了单次充电行驶里程的概念，并提出了一种基于瞬时优化的等效油耗最低能量管理策略。通过对ECMS、DP和AECMS的燃油经济性进行仿真分析及对比，证明了所提出的AECMS的有效性。其中有以下2点重要发现：

1)在不同的行驶周期和不同的行驶距离下，基于DP的控制策略得到的PHEV的最优SOC轨迹是大致随行驶距离变化的直线。

2)仿真结果表明，在不同的工况和不同的单次充电行驶里程下，本研究中提出的AECMS比传统的ECMS具有更高的燃油经济性。与ECMS相比，AECMS在CD模式下燃料消耗降低了3.50%～8.71%，CS模式下降低了1.11%～2.46%。该控制策略的燃油经济性接近于DP控制策略，且克服了DP控制策略难以实时应用的不足。