充分挖掘物理思想 提升学生核心素养

李庆国 帅厚梅

（江苏省扬州市新华中学，江苏 扬州 22509）

物理思想是物理学科素养的重要组成部分，物理思想对学生科学素养的养成、学习能力的提升有着重要的价值.物理思想教育是物理学科教育的重要组成部分.物理思想是物理学的精髓，是知识转化为能力的桥梁.在物理教学中教师要引导学生充分挖掘物理思想，使物理思想充分显现出来，发挥物理思想对学生核心素养的真正培养作用.下面讨论了如何充分挖掘教材中、习题中蕴含的物理思想，以达抛砖引玉之用.

1 充分挖掘教材中蕴含的物理思想

1.1 理解重要物理概念建立过程中蕴含的物理思想

物理概念是物理学大厦的基石，在教学中通过实验器材演示、多媒体的展示等，让学生概括出物理概念.要让学生建立物理知识体系，必须充分理解这些概念的内涵与外延.最关键的是让学生理解得出概念的过程中所蕴含的物理思想.只有这样，才能触类旁通，才能启迪思维.下面以“加速度”这一重要概念的得出加以分析.

甲：10m/s→20m/s，用时5s；乙：10m/s→20m/s，用时10s；丙：10 m/s→25 m/s，用时10s.

问题1：比较甲和乙，谁速度增加得快？问题2：比较乙和丙，谁速度增加得快？问题3：比较甲和丙，谁速度增加得快？

在实际教学中发现，对于问题1和问题2学生能顺利回答出：甲比乙速度增加快，丙比乙速度增加快.

经询问，学生的方法为：速度增加量相同时，看时间，时间短即速度增加快；时间相同时，看速度增加量，速度增加量大即速度增加快；学生用的实际上就是“控制变量”的思想.

但对于问题3，学生一时回答不出来，因为甲和丙速度的增加量和用时均不同，控制变量的思想看似不好用.

教师启发：仍用控制变量的思想，比较甲丙在相同时间内速度的增加量，而相同时间就取单位时间即1s，则甲丙在单位时间内速度的增加量为多少？

问题4：若甲、乙、丙速度变化情况如下，则甲和乙、乙和丙、甲和丙相比谁速度减小得快？

甲：20m/s→10m/s，用时5s；乙：20m/s→10m/s，用时10s；丙：25 m/s→10 m/s，用时10s.

由于有了前述分析，学生能很快给出答案.

总结：当物体的速度发生变化时，有的变化快，有的变化慢，要比较速度变化快慢只要比较即可，若大，则速度变化就快，反之则慢.物理中将命名为“加速度”的实质就是物体在单位时间内的速度变化量，也就是“控制变量”的思想.

“加速度”对于初学者是比较难理解的，在得出概念的过程中主要用了“控制变量”的思想.用这样的思想，“加速度”概念的得出比较自然，实际教学效果相当好.同时也提问学生，以往学过的哪些概念也是用相同的方法得出的？学生最容易想到的是“速度”.这样不但学习了新的知识，对学过的内容也是一个很好的回忆和总结，起到“学一个带一片”的作用.

1.2 理解物理规律的形成过程中蕴含的物理思想

物理规律，是物理学中的灵魂，是物理学大厦中的栋梁，物理学就是利用一个个规律去解决实际问题的学科.一个规律的得出往往要经历很长的过程.在教学中，让学生重演重要物理规律的发现过程，让学生感受科学家探究规律过程表现出来的恒心和毅力，更要让学生深刻理解物理规律、领悟规律发现过程中所用的物理思想.这对学生产生科学情感、形成科学态度都是大有裨益的.下面以伽利略研究自由落体运动为例加以分析.

自由落体运动究竟是什么性质的运动？在伽利略那个时代，很多科学家都在研究，但都没有得出令人信服的结论，主要是当时计时技术很难满足测定自由落体时间的要求.当时进行研究主要在实验室进行，现在我们知道，若一个小球从5m自由下落，下落时间也就1s左右.一般实验室高度没有5m高，故时间太短，较难测量.再说当时是滴水计时，这样的工具是不能测量自由落体时间的.这就阻碍了对自由落体运动的进一步研究.

伽利略采用了间接实验的方法，他用一个黄铜小球从阻力很小的斜槽上滑下，并用水钟测定时间，他经过数百次实验，发现一个从静止开始滚下的物体，在连续相等时间间隔内通过的各段距离之比，等于从1开始的一系列奇数之比，即1∶3∶5∶7…结合匀变速直线运动规律可知，小球沿斜槽下滑是匀加速直线运动.

在斜面实验的基础上伽利略将斜面的倾角不断变大，如图1所示.根据前述结论可知，不管倾角多大都应该是匀加速直线运动，只不过加速度大小不一样而已.然后将斜面倾角逐渐增大直到90°，小球仍然应该是匀加速直线运动.当斜面变成90°，小球沿槽下滑时跟槽之间没有力的作用，也就是小球就是做自由落体运动了，即自由落体运动为初速度为0的匀加速直线运动.

图1

伽利略采用了一个巧妙的方法来“冲淡”重力，小球在斜面上运动的加速度，要比它竖直下落的加速度小得多，所用时间长得多，所以容易测量.在此基础上再进行合理外推，得到自由落体运动为初速度为0的匀加速直线运动这一重要结论.“弱化”重力真的是一个特别有创意的思想.从斜面外推到竖直，这种合理外推是将实验和逻辑推理有机结合起来.伽利略“理想斜面实验”也采用了相同的思想方法.这样的思想方法开创了物理研究的先河.爱因斯坦和英费尔德在《物理学的进化》中评论说：“伽利略的发现以及他所应用的科学的推理方法是人类史上最伟大的成就之一，而且标志着物理学的真正开端”.

在很多规律得出的过程中，都蕴含着令人拍案叫绝的思想方法，比如库仑定律的得出.18世纪中期物理学家既没有度量带电体所带电荷量多少的方法，也没有测量电荷之间非常小的相互作用力的工具.法国人库仑凭着物理学家敏锐的直觉，断定一个带电金属球与另一个半径、材料完全相同的不带电的金属球接触后再分开，每球的带电量应该是原带电球电荷量的一半，从而巧妙地解决了金属球所带电量成倍变化的问题，这种方法可叫作“倍分法”.类似这样的事例还有很多很多，这里不再一一赘述.

在教学中不但要让学生体会科学研究的艰难，让学生对知识有“敬畏感”，更要充分揭示得出规律过程中蕴含的物理思想，让这些有价值的物理思想方法“浮出水面”.教学过程中教师要将这些隐性的物理思想方法作为教学内容的一部分，将其明朗化、显性化、条理化地提出来并有机融入知识传授过程中，启迪学生的思维，调动和激发学生学习兴趣.

1.3 挖掘教材插图中所蕴含的物理思想

物理教材中有大量的插图，插图是一种很好的教学资源.许多插图中蕴含着很多的物理思想，只有把蕴含的物理思想充分挖掘出来，才能真正发挥插图的教学作用.

在曲线运动这一节，为了说明物体做曲线运动速度方向，书上有一幅插图如图2所示，教师应该引导学生思考图中蕴含的物理思想：若物体这一段时间内从A运动到B点，则在AB这个过程中平均速度的方向由A指向B，而当B点越来越靠近A，则AB这个过程中平均速度的方向沿AB连线越来越接近A点的切线方向.当B与A点的距离接近0时，则AB平均速度即在A点的瞬时速度方向就是A点的切线方向，由此得到这样的结论：做曲线运动的物体在某一点瞬时速度方向，沿曲线在这一点切线方向.

图2

插图中蕴含了“极限”的物理思想，将瞬时速度这个比较抽象的问题，用比较直观的方法进行解决.极限思想对许多具有瞬时性的物理概念的建立均有指导，如瞬时加速度、瞬时功率、瞬时电动势等.将“极限”思想迁移到物理学其他分支，就能比较顺利地实现物理量从平均值到瞬时值的过渡，同时也实现了对物理对象粗略认识到精细认识的升华.

在讲弹力的时候，我们知道不管多大的力都可以使物体产生形变，有的形变比较明显，有点形变比较微小，微小形变怎么能显示呢？书上有插图如图3所示.给桌面施加一个压力，桌面发生的是微小形变，微小形变放大如何显示呢？引导学生思考：桌面受力后向下“凹陷”，两平面镜由竖直变成倾斜，则经平面镜反射后的光斑会沿标尺移动.反之，通过光斑的移动，说明桌面发生了形变.

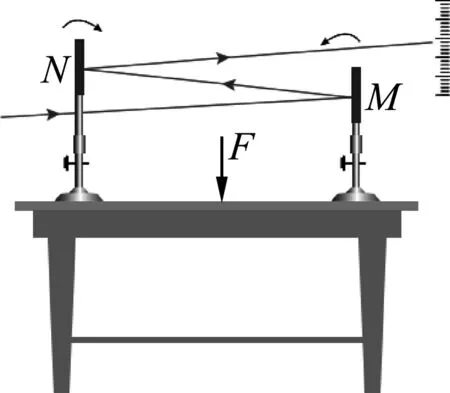
图3

通过光斑移动来间接的显示桌面的形变，这是一个“转化”的思想，也是一个“放大”的思想.可以再激发学生思考，为什么要用二次反射呢？这是多次放大的思想.同时可以再启发学生思考，还有很多地方也是用这样的方法.比如说一个电路中是否有电流，你们无法用肉眼观察到，可以看灯泡是否亮，也可以看串在电路中的电流表的指针是否偏转.这样的例子还有很多.通过这些思想将“看不见摸不着”的东西直观的显示出来，这就是一种重要的思想.

教材插图是教学内容的一个重要补充，教师在教学中要充分运用这些素材，挖掘插图中所蕴含的物理思想，真正发挥插图的教学功能，提升学生能力，更好落实物理学科核心素养.

2 充分挖掘习题中蕴含的物理思想

2.1 体会题目设计中包含的物理思想

例1.跳伞运动员做低空跳伞表演，他在离地面224m高处，由静止开始在竖直方向做自由落体运动，一段时间后，立即打开降落伞，以12.5m/s2的平均加速度匀减速下降，为了运动员的安全，要求运动员落地的速度最大不得超过5m/s（g取10m/s2），问：

（1）运动员打开伞时，离地面高度至少为多少？

（2）运动员着地时速度为5m/s，则相当于从多高处自由落下？

解析：第（1）问不再讨论，着重讨论第（2）问，求解方法很多，故过程忽略，结果为1.25m.第（2）问应该说很简单，出题者究竟想考我们什么？难道仅仅是为了考查学生对基本公式的运用吗？在实际教学中我的确提出过这个问题，学生面面相觑，无法回答.

落地速度太大，人会受伤，但通常人对速度的大小，可能没有太大的感觉，而对长度、高度可能感觉更直观一些.如果人从高1.25m的墙上跳下是否会受伤，学生应该可以轻易判断的.

题目的本意是让我们体会转化的思想，把对速度大小比较抽象的认识转化为对高度比较直观的认识.在这问中还体现了把所学知识应用于生活的思想，知识不会应用就是“无用”的知识.

例2.水分子直径约为4×10-10m，若把9g水的分子一个挨一个紧密排成单行，则可绕地球赤道约多少圈？（赤道周长约为4×10-10m）

解析：水的摩尔质量为18g/m o l，则9g为0.5m o l，近似取NA=6×1023m o l-1，则水分子总数n=0.5NA=3×1023，则一个挨一个紧密排成单行，总长s=n d=1.2×1014m，则绕赤道的圈数为

通过这个题目让学生熟悉与阿伏伽德罗常数相关的计算，想说明组成物质的分子数是大量的.哪怕是看似很小的宏观物体，组成它的分子数也是大量的，但大量怎么体现呢？因为分子是很小的，肉眼看不出，故对大量没有直观印象.题目通过转化的思想将“大量”通过绕赤道的圈数来体现，一是将“大量”直观化，二是通过绕赤道的圈数之多让学生更加理解组成物体的分子是“大量”的概念.转化成一个宏观的现象，可能会让学生更感震撼.这样对阿伏伽德罗常数，对大量的概念会理解得更深.在教学中若想让学生更震撼，理解更深，还可以再进行补充，如学生1s喝进去1000 0个水分子，9g水需要多长时间才能喝完？通过计算，一年若按365天算，则喝完9g水约需9.5×1016年.这样学生对“大量”应该会彻底理解到位，可能一辈子也不会忘.

只有充分理解题目中所包含的物理思想，才能将题目的真正作用发挥出来，才能体现题目的价值，否则就是为了解题而解题，显得枯燥无味，也就失去了学习物理的真正的意义和作用.

2.2 在题目分析中凸显物理思想

为了巩固所学知识，解题是必不可少的，但关键是在题目分析时，一定要凸显解题的物理思想.这样对学生的学习才有帮助，才能使学生在解决问题时养成思考习惯，学习力才能不断增强，下面举一例说明.

例3.运动学中有人认为引入“加速度的变化率”没有必要，然而现在有人指出“加速度的变化率能引起人的心理效应，车辆的平稳加速（即加速度基本不变）使人感到舒服，否则人感到不舒服.关于“加速度的变化率”，下列说法中正确的是

（A）从运动学角度的定义，“加速度的变化率”的单位应是m/s3.

（B）加速度的变化率为0的运动是匀速直线运动.

（C）若加速度与速度同方向，a-t图像如图4所示，表示的是物体的速度在减小.

（D）若加速度与速度同方向，a-t图像如图4所示，已知物体在t=0时速度为5m/s，则4s末的速度大小为17m/s.

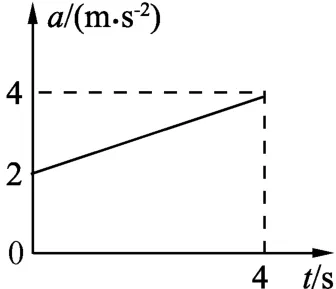
图4

解析：在实际教学中发现，（A）、（B）、（C）选项以大多数学生的能力都能准确判断，但（D）选项感到困难.在解决此问题时，我为学生设立了一个台阶，模仿（D）选项的问题：若物体加速度与速度同方向，a-t图像如图5所示，已知物体在t=0时速度为5m/s，则4s末的速度大小为多少？

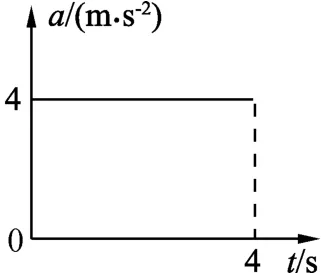
图5

对于这个问题，学生很快就给出了答案.再问学生4 s内物体速度的增加量多大？图像与坐标轴围成的面积的值是多少？能找出他们之间的关系吗？学生们都得到了“图像与坐标轴围成的面积的值等于物体速度的增加量”这一结论.接着再问，能不能把这个结论直接迁移到图6这种情况？此时出现了不同答案，有的说行，有的说不行.笔者不置可否.

图6

提示学生将物体运动时间平均分成n段（n→∞），每一段时间为Δt，如图6所示.由于每一段时间极短，故可认为在每一段极短时间内加速度是恒定的，故由前述结论可知：图像与坐标轴围成的面积的值等于物体速度的增加量.依此类推，每一个Δt均有同样的结论，故可得到0—4s内图像与坐标轴围成的面积的值等于4s内物体速度的增加量，计算可得Δv=12m/s，即4s物体速度为17m/s.

得出结果后，一定还要跟学生讲清分析过程中运用了如下物理思想.

（1）用匀变速结论推出非匀变速结论，充分体现了用已知推未知，从简单到复杂的物理思想.

（2）将运动时间无限分段，即使全过程加速度是变的，但每一段可以认为是恒定不变.这样在每一段就可以运用已有结论，充分体现了“化变为恒”的思想.

（3）无限分割实际使用的也就是“微元”的思想.“微元法”在中学阶段用得也很多，教师也可以借机让学生回忆一下，在推导匀变速直线运动的位移与时间关系时就用了“微元法”.这样学生就觉得有似曾相识之感，接受起来就不会觉得很陌生.

在进行题目分析时，一定要将所用的物理思想凸显出来，一是让学生体会运用知识解决问题的过程.二是让学生感知知识的魅力，不断引导学生学会思考，激发斗志，最终达到能力的提升.

物理思想是物理知识及物理方法的灵魂.物理思想具有隐蔽性、抽象性和创造性，它蕴含在知识的发生、发展和应用的过程中.传统物理教学往往是重视必考知识的传授和解决能力的培养.随着新课程改革的实施，教师一定要改变这种状况.只有使学生在进行物理课程学习时，深入到对于物理思想的了解和挖掘，才能够形成系统的、完善的物理学科学习理念.掌握物理学习的精髓，才能够为学生今后的发展开辟一个全新的学科领域，真正使学生感受到物理的奥秘和魅力.