基于块对角化的通信雷达频谱共存设计

韩凯峰，黄立涛，陈力，王志勤

（1.中国信息通信研究院移动通信创新中心，北京 100191；2.中国科学技术大学电子工程与信息科学系，安徽 合肥 230026）

1 引言

随着移动设备的爆炸性增长以及其他射频应用的迅速扩张，无线电频谱正变得越来越拥挤[1]。对于6 GHz 以下的频段，大多数商业通信系统工作于此，然而同频段工作的还有用于气象观测和交通控制等任务的雷达系统[2]。被汽车雷达和高分辨率成像雷达所占据的毫米波频段，现在也要将其作为许可频段分配给5G 网络[3]。可以预见，频谱拥挤的现象将进一步加剧。为了更加高效地利用频谱资源，解决通信和雷达同频共存的问题，学术界和工业界对通信雷达频谱共存（CRC,communication-radar coexistence）[4-5]进行了大量的研究。根据文献[6]可知，通信雷达频谱共存指的是通信和雷达系统在同一频段共存并同时运行，需要设计其中一套系统的发射波束或者分别设计两者的发射波束，去消除它们之间的干扰，从而保证两套系统能正常工作。

由于雷达系统有其特定的性能指标，而传统的认知无线电技术[7]只考虑了具有相同性能指标的通信系统间频谱共存，不能直接用于通信雷达频谱共存问题。关于通信雷达频谱共存，文献[8]考虑了机会性频谱共存，它将旋转雷达设为频段的主要用户，通信系统设为频段的次要用户，通信系统工作的前提是其发射功率不超过雷达所允许的干扰信噪比。值得注意的是，以上的方法仅仅允许通信系统在特定条件下才能正常工作，且只考虑了相控阵雷达，一旦雷达换成全向发射的多输入多输出（MIMO，multiple-input multiple-output）雷达，系统的性能将急剧下降。基于MIMO 通信下的迫0预编码[9]，文献[10]通过不对通信系统进行任何改变，将MIMO 雷达波形投影到雷达与通信系统之间干扰信道矩阵的0 空间上，牺牲MIMO 雷达的一部分性能换取对通信系统的0 干扰，作为MIMO 雷达与通信系统在同一频段共存的解决方案。文献[11]在文献[10]的基础上，将MIMO 雷达波形投影到干扰信道矩阵0 空间的扩展子空间上，引入了一定量对通信系统的干扰。通过保证MIMO 雷达对通信系统的干扰低于预先设定好的阈值，既减少了对MIMO 雷达性能的牺牲，又保证了MIMO 雷达与通信系统在同一频段正常工作。文献[12]采用交替优化的算法，在通信系统发射功率和系统容量的约束下，联合优化MIMO 雷达的采样方案和MIMO 通信系统的波束成形矩阵，使MIMO 通信系统对MIMO 雷达造成的干扰达到最小化。为了进一步解决更加实际的多用户情况，文献[13]考虑了多用户MIMO 通信系统和MIMO 雷达间的频谱共存，利用已知的通信用户间干扰，在通信系统的发射功率和信干噪比的限制条件下，通过设计通信系统的波束成形矩阵，从而最大化雷达的检测概率。文献[14]考虑了在不完美信道状态信息的情况下，多用户MIMO 通信系统和MIMO 雷达的频谱共存问题，使设计出的通信波束成形矩阵更具备稳健性。

由于是通信系统在雷达频段上进行频谱共享，那么雷达系统作为频段的拥有者，不能要求其改变自身的工作模式，同时通信系统也不能对其造成干扰。但是上述的相关工作如文献[10-11]考虑的是雷达系统接入通信频段，文献[12-14]考虑的是重新设计通信和雷达系统的发射波形，都不符合这种场景。所以本文考虑将一个多用户MIMO 下行通信系统接入MIMO 雷达频段，通过设计通信系统的波束成形矩阵，在对雷达不造成任何干扰，以及满足自身发射功率限制的条件下最大化通信系统的和速率。由于该问题数学建模后非凸且不具备解析解，因此本文引入了一种基于块对角化（BD,block diagonalization）的低复杂度波束设计，通过增加用户间干扰为0 这一约束条件，从而使原问题具备解析解。但是，增加的约束条件会限制通信系统收发两端的天线数。所以本文进一步考虑了在不满足限制条件的情况下，将块对角化与子信道正交和用户选择这2 种算法结合，放宽了收发两端天线数的限制，从而使原问题在各种条件下都具备解析解。

在本文中，用大写粗体字母表示矩阵，小写粗体字母表示矢量。HH表示矩阵H的共轭转置；标记C 表示复数域；标记表示对实数X向下取整数；标记(A)+表示当A为负数时取0，A为非负数时取A；标记len(B)表示集合B中的元素个数。

2 问题建模

2.1 系统模型

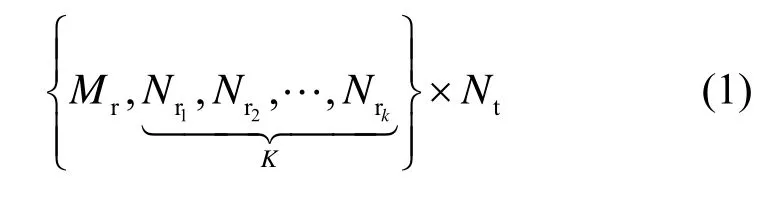
来表示通信系统和雷达系统的发射接收天线数的设置情况。

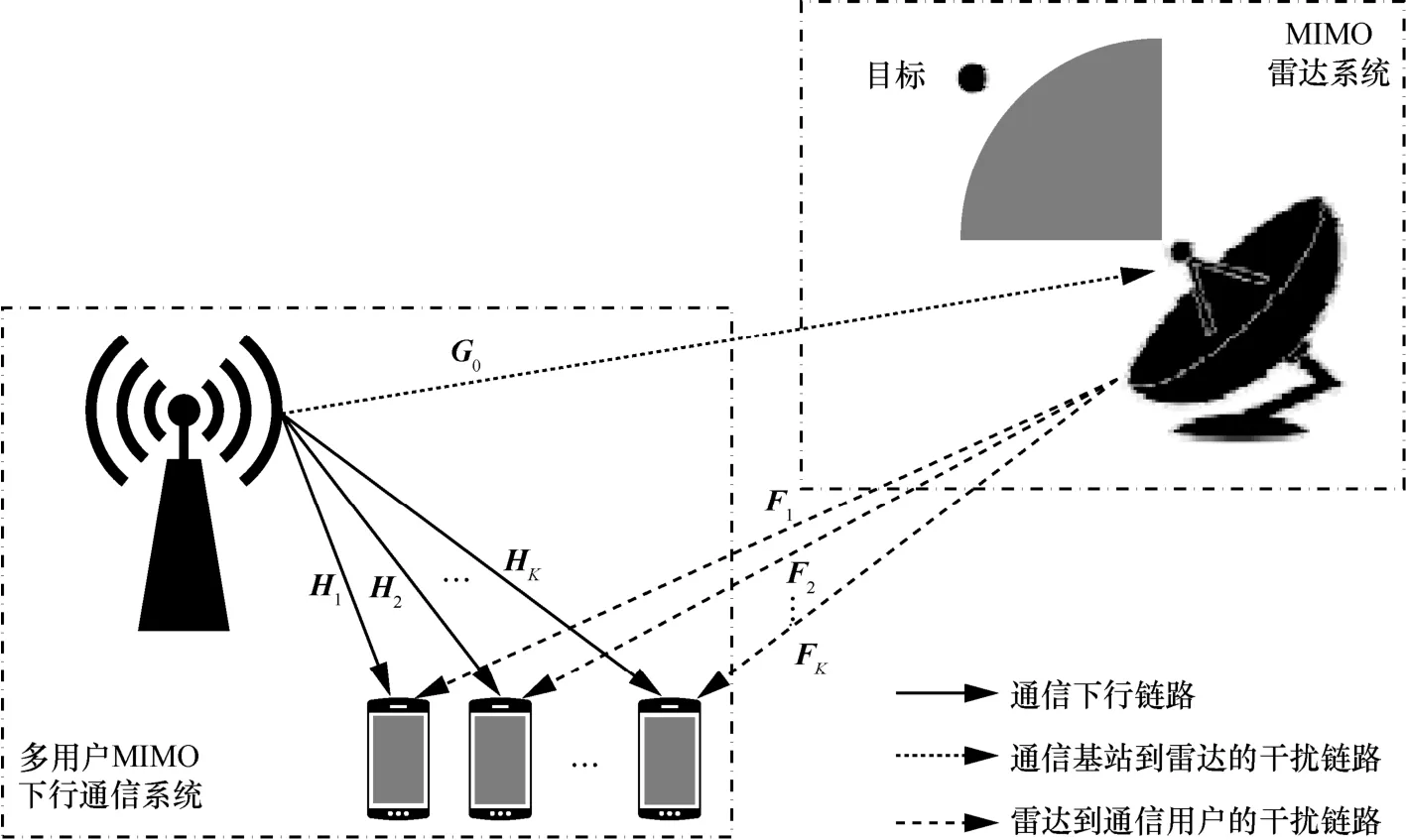
图1 通信雷达频谱共存场景模型

考虑通信用户间的干扰和雷达对通信用户的干扰，假设2 个系统具有相同的符号率，并且在采样时间方面是同步的，那么在L个符号持续时间内通信用户j接收到的信号为

那么通信系统的和速率可以表示为

由于MIMO 雷达将会作为频段的拥有者，故在雷达侧只需要表征通信基站对MIMO 雷达所造成的干扰。根据文献[14]中雷达接收到来自通信基站干扰信号的公式，雷达系统接收到的干扰功率可表示为

2.2 问题建模

本文考虑通信系统接入雷达频段的通信雷达频谱共存场景，即MIMO 雷达系统具有更高优先级。通信系统首先要通过设计发射预编码矩阵，消除通信信号对雷达系统的干扰才能接入雷达频段。完成干扰消除的同时，本文选择了最大化通信系统的和速率作为优化目标。考虑到通信系统和速率的最大值总在通信基站的发射功率等于门限值时取到，所以在保证对雷达系统不造成任何干扰以及符合通信基站自身功率限制的前提下，通信系统和速率最大化问题可以建模为

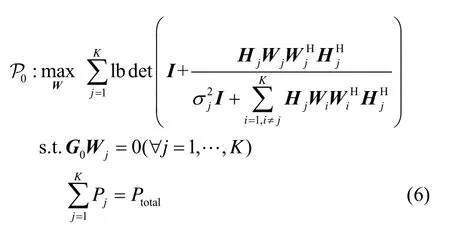
其中，Pj是分配给第j个通信用户的发射功率大小是基站总的发射功率大小，Ptotal是基站发射功率的门限值是由通信用户j的接收噪声和雷达系统对通信用户j的干扰噪声叠加而成的混合噪声等效于将通信基站对雷达系统的干扰功率大小置0，即满足通信系统对雷达系统不造成任何干扰，可以通过将波束成形矩阵W投影到干扰信道G0的0 空间上实现。

3 不同自由度下的块对角化算法

由于问题 P0非凸，不具备解析解。但是增加一定的约束条件后，可以获得解析解[15]。受启发于文献[10-11]，本文选择引入HW是块对角的，也就是

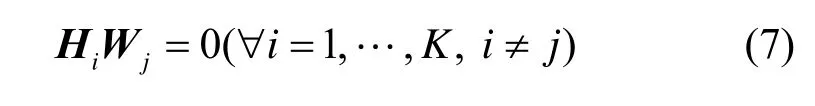
去完全消除用户间的相互干扰。假设中间矩阵定义为

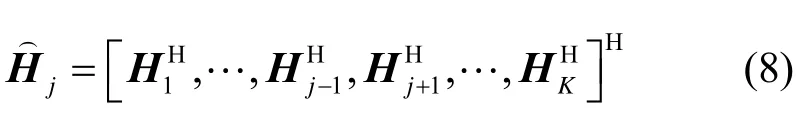
为了完全消除用户间干扰以及保证通信用户j能够接收到数据，需要将波束成形矩阵Wj投影到中间矩阵的0空间上，并且0空间的维度必须大于0。也就是通信系统的发射天线数需要满足

才能引入式(7)这一约束条件。式(9)中加入MIMO雷达的接收天线Mr是因为在满足式(7)完全消除用户间干扰的同时，必须要保证通信基站对雷达不造成任何干扰，所以还需要将波束成形矩阵投影到信道G0的0 空间上。当通信系统的发射天线数满足式(9)时，问题 P0可以写成

对问题 P1，本文提出了低复杂度、非迭代的CRC BD 算法来求解。

由于式(9)对天线数的限制，CRC BD 算法对于所能容纳的最多通信用户数也有所限制，因此对各个通信用户的接收天线数做出了假设。当时，CRC BD 算法所能容纳的最多通信用户数为

但装有Nt个发射天线的基站总可以发送Nt个无干扰的数据流，意味着装有Nt个发射天线的基站可以最多容纳Nt个用户。所以当通信基站的发射天线数无法满足式(9)、用户数时，本文提出了CRC Modified BD 算法，将式(9)放宽为

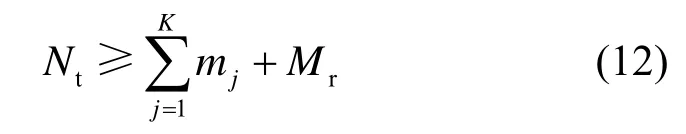
其中，m j表示第j个通信用户选取的子信道数目且因此当通信用户数

时，还可以引入式(7)使问题 P0具备解析解。

最后本文提出了基于贪心选择的CRC User Selection 算法，该算法考虑从庞大的用户集中选取次优的用户子集来满足CRC BD 算法的天线条件。当通信用户数

时，仍旧可以引入式(7)使问题 P0具备解析解。

3.1 CRC BD 算法

根据上述讨论，当通信基站的发射天线数目满足式(9)，即通信用户数满足式(11)时，问题 P0可以写成问题 P1，并由CRC BD 算法求解。该算法就是在满足通信基站功率限制的条件下，找到合适的波束成形向量使基站对雷达的干扰为0 以及通信用户间的干扰为0，从而最大化通信系统的和速率。所以需要将第j个用户的波束成形向量Wj置于通信基站到通信用户信道链路和通信基站到MIMO 雷达信道链路G0的0 空间上。引入中间矩阵定义为

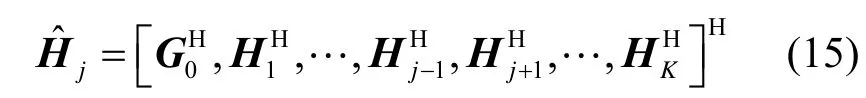
那么当波束成形向量Wj位于矩阵的0空间内时，就能满足通信基站对雷达以及通信用户间的干扰为0。

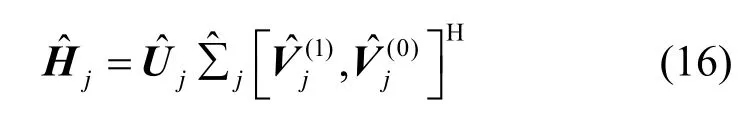
3.2 CRC Modified BD 算法

CRC BD 算法的基本思想是将基站到雷达以及基站到各通信用户之间的信道链路相互正交。但是在某些情况下，如通信系统处于低信噪比时，基站到用户信道链路中某几条子信道的信道增益会趋于0，因此CRC Modified BD 算法仅仅考虑各条信道的主导子信道，即信道增益较大的子信道之间相互正交，引入一定量用户间干扰的同时，将省下的空间自由度容纳更多的通信用户，从而提升通信系统的和速率。那么问题 P1可以重新写成

这样就完成了各条信道主子信道的选取。定义中间矩阵

3.3 CRC User Selection 算法

当通信用户数K＞Nt-Mr时，上述2 种算法由于分别受限于式(9)和式(12)，将不再满足必要的收发天线数限制条件，但可以应用CRC User Selection算法引入式(7)的约束，使原问题 P0具备解析解。此时，问题转换为对通信用户数K＞Nt-Mr的多用户通信系统来说，如何选择一个用户子集来满足CRC BD 算法的天线条件，从而使通信系统和速率最大化。显而易见，在所有可能的用户集上进行穷尽搜索，可以得到一个最优的用户子集。然而，如果通信系统中的用户数很大，其复杂性是令人望而却步的。例如，如果是CRC BD 算法可以同时支持的最大用户数，K是用户总数，那么穷尽搜索的算法复杂度大致为而本文提出的CRC User Selection 算法作为一种次优算法，将复杂度降为的同时，性能却能够极大地靠近最优解。假设每个用户都利用其所有的接收天线且通信用户的接收天线数量保持一致，都为Nr。那么CRC User Selection 算法就是在保证对雷达系统干扰为0 的情况下，从K个通信用户中选取最多个用户组成用户集S，应用CRC BD 算法，从而最大化通信系统的和速率。

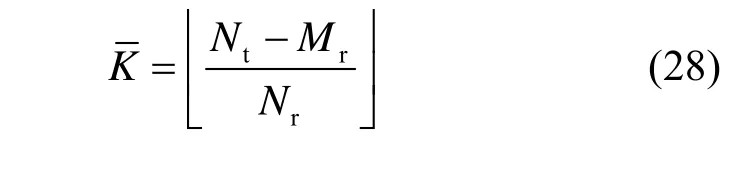
令Ω表示未选择用户的集合，S表示已选择用户的集合。CRC User Selection 算法首先选择吞吐量最大的单个用户；然后从剩余的未选择用户中，找到与这些被选择的用户一起提供最大和速率的用户。当用户集S选满了K个用户，或者新选择的用户使通信和速率下降时，该算法就会终止（由于为了满足用户间0 干扰的要求，每个用户的0 空间大小都会减小，因此总吞吐量可能会随着增加一个用户而降低[17]）。显然，所提算法在不超过KK个用户集上进行搜索，与穷尽搜索方法相比，大大降低了复杂度。CRC User Selection 算法（算法3）的具体步骤如下。

算法3CRC User Selection 算法

4 仿真实验

在进行仿真实验前，首先通过表1 列出不同收发天线数和通信用户数限制条件下所适配的算法。从表1 中可以观察到，本文提出的3 种算法能在大部分的场景下求解原问题 P0。

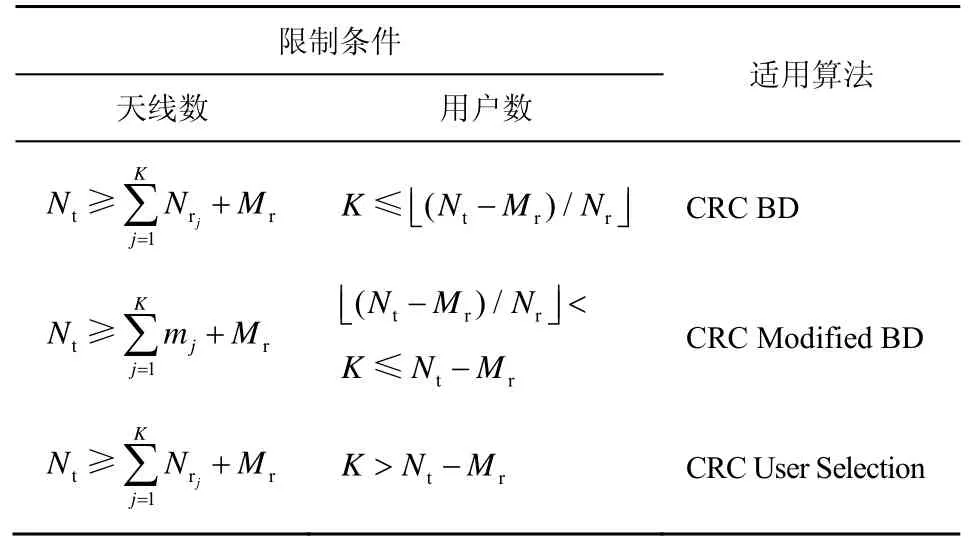
表1 各限制条件下所适配的算法

以下将基于若干常用假设及不同仿真参数来进一步仿真验证本文提出的3 种算法的性能，仿真实验结果都是基于1 000 次仿真计算的平均值。首先，假设所有信道链路的信道状态信息元素均为独立且同分布的复高斯随机变量，且混合噪声均值为0、方差为1，上述假设为相关研究文献[12-13]中的常用假设。其次，在图2～图6 中，假设信道估计非常准确（即信道状态信息完美已知），用以验证3 种算法的有效性。在图7 中，假设信道估计结果存在不同程度的误差，用以初步验证本文提出算法的稳健性。具体表示为：基于文献[13]中的信道估计误差模型，将信道矩阵建模为其中表示估计的信道矩阵；e0和ej分别满足，表示信道状态信息的不确定度。假设通信基站处对和已知，但对e0和ej具体值未知（仅知其范数的范围

图2 显示了在CRC BD 算法下，改变通信用户数量K后的通信系统和速率与通信基站发射功率之间的关系。仿真条件为：当K=1时，系统的天线配置为{2,2} × 4；当K=2时，系统的天线配置为{2,2,2} × 6；当K=3时，系统的天线配置为{2,2,2,2} × 8。天线配置的表示形式含义与式(1)中定义一致，以上天线配置均为满足CRC BD 算法所必要的天线条件。CRC BD/WF 代表使用注水算法来进行功率分配后的 CRC BD 算法；CRC BD/AVE 代表使用平均功率分配后的CRC BD 算法；CRC BD/R 代表使用随机功率分配后的CRC BD 算法，基本思想是将总功率大小按照随机的方式分配给各个通信用户；CRC BD/A 代表使用基于天线选择功率分配后的CRC BD 算法，基本思想是根据信道质量的优劣来进行功率分配。

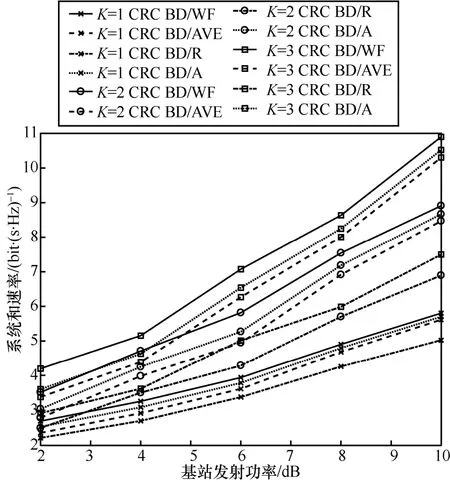
图2 CRC BD 算法下和速率与通信用户数的关系

从图2 中可以观察到，本文提出的CRC BD 算法在保证对MIMO 雷达干扰为0 的前提下，随着通信基站的发射功率提升，系统的和速率也相应增加。并且固定基站的发射功率后，随着通信用户数量的增加，通信系统的和速率也会稳步提升。在相同条件下，当CRC BD 算法中功率分配这一步骤采用其他算法时，可以观察到使用注水算法进行功率分配较其他3 种功率分配算法能取得更好的性能。

图3 基于图2 中K=3的CRC BD 算法，固定通信用户数和接收天线数不变，改变通信基站的发射天线数。系统的天线配置为{2,2,2,2} × 8、{2,2,2,2} × 10和{2,2,2,2} × 12。从图3 中可以观察到，当通信基站的发射功率相同时，随着通信基站的发射天线数增加，应用CRC BD 算法后的通信系统和速率也相应提升，进一步说明了算法的有效性。同时，随着发射天线数目的增加，平均功率分配下的CRC BD算法和基于天线选择功率分配下的CRC BD 算法与使用注水算法进行功率分配的CRC BD 算法相比，它们的性能差距不断缩小。

图3 CRC BD 算法下和速率与通信基站发射天线数的关系

图4 显示了在固定雷达和通信用户接收天线数都为两根的条件下，对CRC Modified BD 算法和使用注水算法进行功率分配后的CRC BD 算法，通过改变通信基站的发射天线数，分别选取满足式(9)和式(12)所能容纳的最大用户数K，从而进行性能比较。在保证容纳最多用户的前提下，当通信基站的发射天线数分别为4 根、6 根和8 根时，根据式(9)，CRC BD 算法的天线配置分别为{2,2} × 4、{2,2,2} × 6和{2,2,2,2} × 8；根据式(12)，CRC Modified BD 算法的天线配置分别为{2,2,2} × 4、{2,2,2,2,2} × 6和{2,2,2,2,2,2,2} × 8。从图4 中可以观察到，在相同的条件下，CRC Modified BD 放宽了CRC BD 的天线限制条件，通过引入一定量的用户间干扰，从而可以容纳更多的通信用户，因此取得了更好的性能。

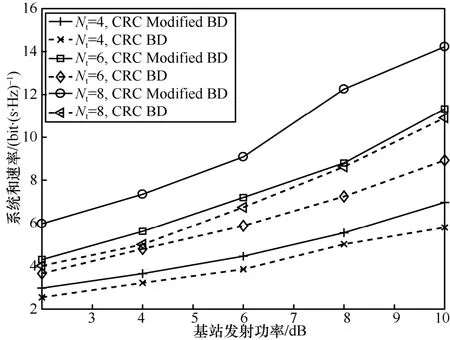
图4 CRC Modified BD 算法下和速率与通信基站发射功率的关系

图5 考虑了当通信用户数远大于CRC BD 算法所能容纳的最多用户数时，应用 CRC User Selection 算法后得到的系统性能与最优解之间的差距。天线配置为{2,2,2,2} × 8，此时通信系统能容纳的最多用户数那么CRC User Selection算法就是要从一个大用户集中最多选取3位通信用户最大化通信系统的和速率。Optimum 代表最优解（即穷举式算法）；C-max 代表从大用户集中选取信道容量最大的前3 位通信用户；F-max 代表从大用户集中选取信道状态最好的前3 位通信用户；Random 代表从大用户集中随机选取3 位通信用户，作为算法性能基线。根据仿真结果，所提算法能够实现的通信系统和速率约为最优解的95%左右。并且在低信噪比的情况下，所提算法实现了几乎与最优解相同的性能，这是因为算法的第一步是对速率最大的用户进行波束成形，对于低信噪比情况下CRC BD算法的和速率而言是渐近最优的。对于高信噪比，尽管所提算法因搜索范围缩小很难找到最优的用户子集，但由于每一步迭代都是基于使通信系统的和速率达到最大化，因此它仍可以在低计算复杂度的情况下，性能接近最优解。而F-max 算法和C-max 算法仅分别选取了信道质量最好的和信道容量最高的前个用户，所以性能只是优于随机选取算法。

图5 CRC User Selection 算法下和速率与总通信用户数的关系

图6 比较了各个用户选择算法的计算复杂度。从图6 观察可得，最优解运行一次算法的时间随着总通信用户数的增加，呈指数级增长趋势。而本文所提算法虽是一种迭代算法，但运行一次算法的时间随着总通信用户数的增加呈线性增长，同时还能达到最优解性能的95%，说明本文提出的CRC User Selection 算法具备可行性，且复杂度相对较低。由于其他2 种用户选择算法是非迭代的算法，只需要根据各个通信用户信道的容量或者信道的质量来选取前个通信用户，涉及的仅是排序算法，因此计算复杂度较低，但也带来较大的性能损失。

图2～图6 中的仿真实验均基于信道估计结果非常准确（即信道状态信息完美已知），但由于在实际情况下信道估计并非完美，存在不同程度的误差。为此，图7 仿真验证了不同程度的信道估计误差对CRC BD 算法性能所产生的影响。由于CRC Modified BD 算法与CRC User Selection 算法在有信道估计误差的情况下具有类似结果，因此不进行重复验证。参数设置如下：信道估计误差模型基于式(29)，天线配置条件为{2,2,2,2} × 8，假设信道不确定度范数的范围。其中，Perfect CSI 代表信道估计信息非常准确（即δ2=0，信道状态信息完美已知），随着δ2的增大，信道估计误差增大。观察图7 发现，当信道估计误差较小（如δ2≤0.1）时，CRC BD 算法性能并未有明显下降（系统和速率下降在0.5 dB 以内），具有一定的稳健性。随着信道估计误差增大，算法性能下降较明显（如δ2=1.0 时，系统和速率下降超过1 dB），因此在后续研究中，需要针对性设计能够适应非完美信道估计下的稳健算法。

图6 各用户选择算法运行一次时长与总通信用户数量的关系

图7 CRC BD 算法在信道估计不完美情况下的性能分析

5 结束语

本文提出了一种在通信与雷达同频共存场景下基于块对角化的波束设计方案。首先根据具体场景建立了优化问题，提出了块对角化的结构，引入通信用户间干扰为0 的约束，使非凸的原优化问题具备解析解。其次提出了2 种改进算法，放宽了引入约束所带来的关于收发天线数的限制条件。最后通过仿真验证说明了所提算法的可行性及性能效果。本文所提算法性能接近最优结果，且具备解析解、计算复杂度较低，能够简化发射机和接收器结构，实际工程应用价值较高。下一步，将聚焦研究分析信道估计误差对算法性能的定量影响并设计针对非完美信道估计下的最优稳健算法。