主缆纵向不对称特大悬索桥地震反应特性

钱 晋， 华 新， 叶爱君

(1. 同济大学 土木工程防灾国家重点实验室，上海 200092；2. 华设设计集团股份有限公司，江苏 南京 210014)

随着我国经济实力的不断增强和交通事业的不断发展，出现了越来越多的越江工程。悬索桥因其纤巧的造型和极强的跨越能力不仅受到了广大民众的关注和欢迎，而且也得到了桥梁设计师们的研究与重视[1]。我国是世界上地震活动最强烈和地震灾害最严重的国家之一，桥梁工程是交通线路中的节点，其破坏将不仅导致整条线路中断，同时也难以修复[2]。因此，在建设超大跨度悬索桥时，需要重点考虑如何保证桥梁的抗震安全性。

目前，国内外与悬索桥抗震研究相关的内容主要集中在以下几个方面：(1)对某座桥进行详细的非线性分析，提出相应的加固建议或施加减震措施[3～5]。毛勇等[5]以南京仙新路特大跨度悬索桥为例，阐述悬索桥抗震性能研究的全过程，并分析行波效应对该桥地震响应的影响。(2)对悬索桥进行地震地面运动空间效应方面的研究，如行波效应、多点激励。阳威等[6]研究发现，对于大跨度悬索桥，多点激励行波效应对各桥塔塔底内力、塔顶位移、梁端位移及塔梁相对位移影响不同。刘立鹏等[7]通过对一跨长江大跨度悬索桥的模态分析，分析了大跨桥梁的频谱特性及振动特点。(3)通过随机振动分析来提高地震激励的计算效率。刘小璐等[8]基于相对运动法推导了非一致地震激励下结构动力响应的时域显式表达式，可高效计算结构抗震动力可靠度。

大跨度悬索桥的已有抗震研究大多针对对称结构，对于主缆不对称悬索桥的抗震研究较少。目前，由于江河两岸的地质环境差异或引桥布置需要，我国已建设了不少主缆不对称布置的悬索桥。杨国俊等[9]基于ANSYS软件建立了某大跨度主缆不等高支承悬索桥的三维有限元模型，研究了大跨度非对称悬索桥的动力特性。

为了研究这类悬索桥的地震反应特性，本文以一主跨1560 m的悬索桥为背景，基于SAP 2000程序建立主缆对称布置和不对称布置的悬索桥有限元模型，分别考虑一致地震激励和非一致地震激励，研究主缆纵向不对称布置对悬索桥地震反应的影响。

1 工程背景与动力分析模型

龙潭大桥位于长江南京段与镇扬段分界处，场地抗震设防烈度为Ⅶ度。主桥采用单跨悬索桥方案，主缆分跨布置为615+1560+552 m。主桥桥塔为钢筋混凝土塔，横向为门式框架结构，主梁为流线型扁平钢箱加劲梁，主塔基础采用52根直径2.8 m的钻孔灌注桩方案，承台截面为哑铃型，支座为纵向滑动横向固定的球钢支座。

针对这一悬索桥，本文基于SAP 2000平台，建立了桥梁空间有限元动力分析模型，如图1所示。图中NT，ST，NA，SA分别表示北塔、南塔、北锚碇、南锚碇。模型中，主缆和吊杆采用桁架单元模拟(杆端释放弯矩和扭矩)，桥塔采用梁单元模拟，主梁采用单主梁式模型，节点通过主从约束与吊杆相连；主缆、主梁和主塔考虑了恒载几何刚度的影响；承台质量堆聚在承台质心，承台刚度根据实际截面赋予对应单元；二期恒载以及附加线荷载以集中质量形式加在梁单元节点上；支座采用线弹性连接单元模拟，滑动方向刚度取小值(10 kN/m)，固定方向刚度取大值(106kN/m)；桩土作用采用六弹簧模拟。

图1 龙潭大桥动力分析模型

基于前述实桥模型，本文拟定了以下三个有限元模型进行比较分析。

(1)对称模型：主缆南北边跨均为615 m，作为基准模型；

(2)南边跨552 m非对称模型：实桥模型，主缆北边跨615 m、南边跨552 m；

(3)南边跨300 m非对称模型：主缆北边跨615 m、南边跨300 m。

为了突显主缆不对称布置的影响，三个模型均不考虑南北两侧相邻联引桥对主桥地震反应的影响。

2 地震输入

本文基于桥址场地地震安全性评价报告，选用了地震重现期为2500年的地震动参数作为地震动输入，包括地震加速度设计反应谱和7条地震加速度时程。图2a给出了7条地震加速度时程对应的反应谱与设计反应谱，而图2b则代表性地给出了其中一条地震加速度时程曲线。本文在时程反应分析中，对每一条地震加速度时程均进行了计算，结果取平均值。

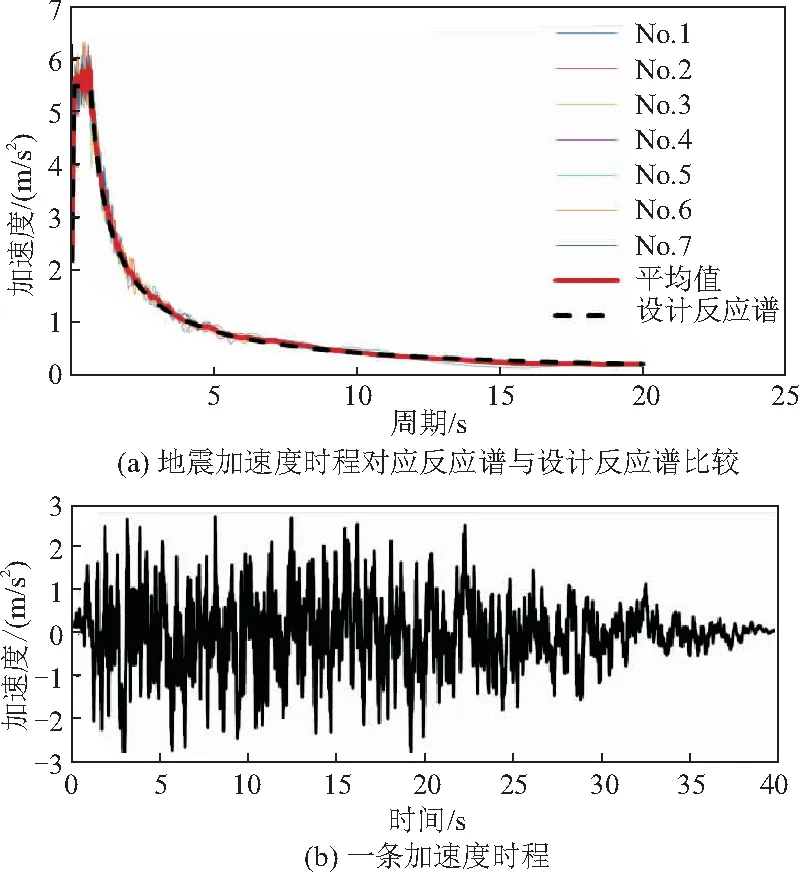
图2 地震动输入

3 动力特性分析

分析和认识桥梁结构的动力特性是进行抗震性能分析的基础。因此，本文首先对所建立的三个有限元模型进行了动力特性分析，并对主要振型及对应周期进行了比较，如表1所示。

由表1可知，主缆边跨不对称布置对悬索桥的振型及周期影响很小，主要是会影响主塔侧弯振型的对称性及纵弯振型的周期。主缆南边跨的跨度从615 m减小为300 m时，主塔的侧弯振型周期只减小了5.4%，纵弯周期也只减小了4.6%。南边跨主缆长度随跨径减小而减小，其对南塔的约束作用增强。

表1 主桥动力特性比较

4 一致激励下的地震反应特性

一致激励下的地震反应分析可以采用时程分析法和反应谱分析法，反应谱方法中各振型阻尼比保持不变，而时程分析法通常采用瑞利阻尼假定，各振型阻尼比取决于所选择的两阶控制频率。为了避免瑞利阻尼的确定对地震反应的影响，本文采用更易全面反映规律的反应谱方法分析一致激励下主缆纵向不对称布置对悬索桥地震反应的影响，分别沿纵、横、竖三个方向进行地震输入，计算了前1500阶振型的贡献，振型组合采用CQC(Complete Quadratic Combination)法。

表2列出了一致激励下南北塔塔底截面的最大地震内力，结果可见，主缆南边跨小幅减小(减小幅度10%)对主塔地震内力的影响可以忽略，但南边跨大幅减小(减小幅度50%)会对主塔地震内力有明显影响。主缆南边跨减小50%对横向地震作用下的塔底内力影响很小，但会显著影响纵向地震作用下塔底轴力(南塔增大60%)和弯矩(南塔减小22%)，以及显著影响竖向地震作用下的塔底剪力(南塔增大40%)和弯矩(北塔增大34%)。但是，需要注意到，纵、横向地震作用下的塔底剪力和弯矩远大于竖向地震作用的贡献，而竖向地震作用下的塔底轴力远大于纵向地震作用的贡献。因此，在规范要求的纵向+竖向、横向+竖向地震作用下，主缆南边跨大幅减小主要会影响南塔的纵向地震弯矩。

表2 一致激励下南北塔地震反应分析

表3列出了纵、横向地震作用下主梁梁端及塔顶最大地震位移，可以看出主缆南边跨跨径的减小对塔顶横向地震位移和主梁纵向地震位移影响很小，但会明显减小塔顶纵向地震位移，当主缆南边跨跨径减小一半时，南、北塔塔顶位移最大分别减小40%和18%。主缆南边跨跨径的减小增大了主缆系统的刚度，但主缆对塔顶纵向位移的约束作用较强，对横向位移约束作用较弱。

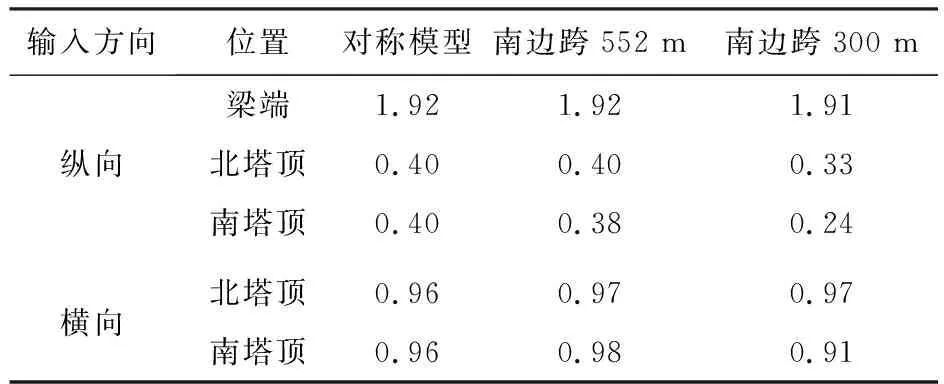
表3 关键位置地震位移比较(E2地震输入) m

5 非一致激励下的地震反应特性

现行规范JTG/T 2231-01-2020《公路桥梁抗震设计规范》[10]指出当桥梁一联内场地存在地质不连续或地形特征可能造成各桥墩的地震动参数显著不同，或桥梁一联总长超过600 m时，宜采用多点非一致激励考虑地震动的空间变化。本文仅研究行波效应对桥梁地震反应的影响。

主缆纵向不对称布置使得行波效应的影响更加复杂。为了研究行波激励下主缆纵向不对称布置对桥梁地震反应的影响，本文基于前文建立的三个计算模型，取1000，2000，3400，7000 m/s以及∞五组视波速，采用前述7条地震加速度时程进行纵向激励，进行地震反应时程分析，结果取南北两侧输入的地震反应较大值。其中，视波速为∞代表主桥一致激励下的地震响应。

图3给出了南、北塔底的剪力、弯矩随视波速的变化曲线。由图可知：对称模型的塔底剪力弯矩最小，南边跨552 m模型剪力弯矩其次，南边跨300 m模型剪力弯矩最大；视波速对地震反应的影响比较复杂，主缆纵向不对称布置后，地震反应对视波速更为敏感，不同视波速下，对称模型的塔底剪力弯矩最大影响为+10%左右，南边跨300 m模型最大影响为+30%左右。

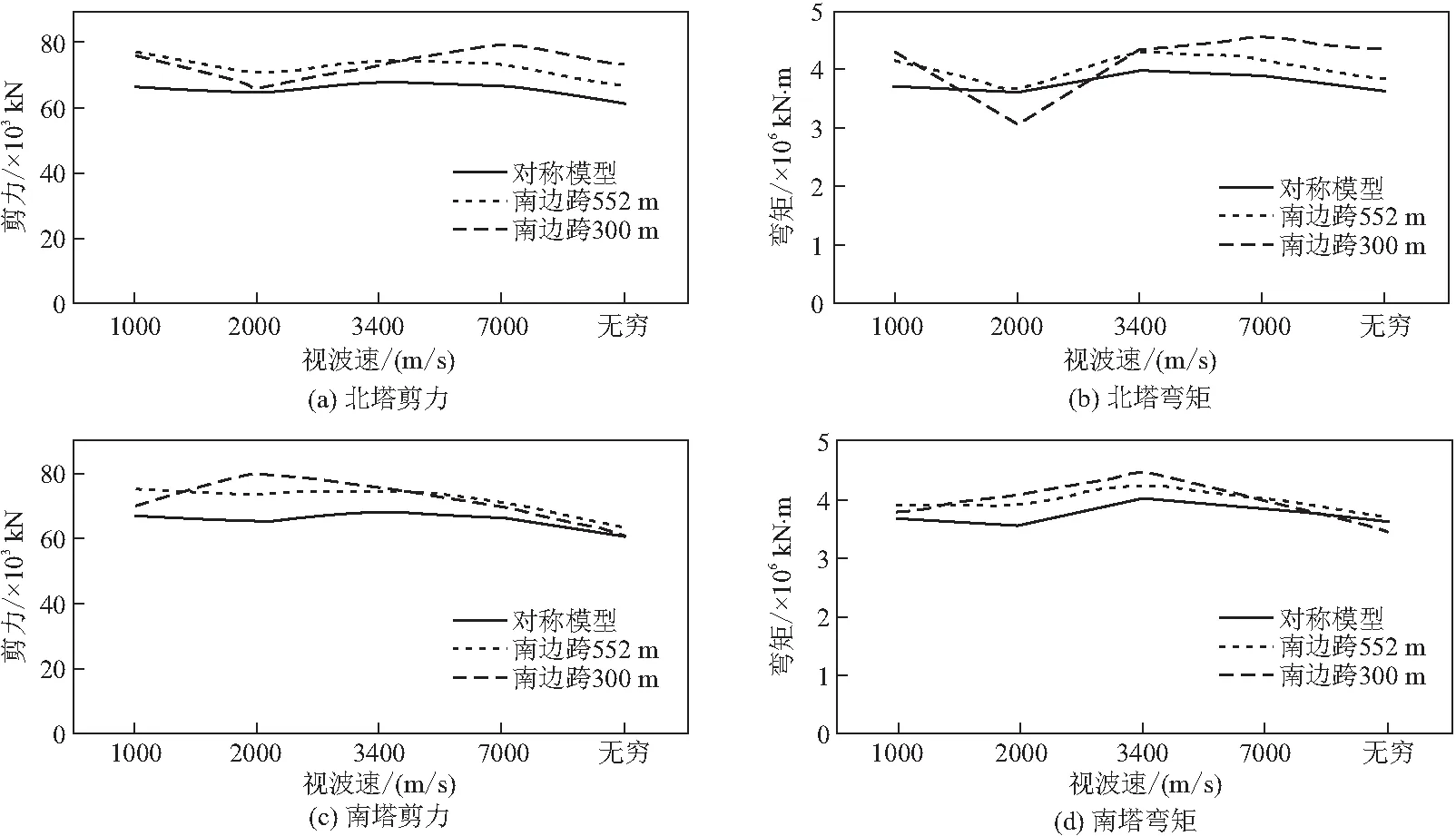
图3 行波效应对塔底内力的影响

图4给出了不同视波速下南、北塔顶和梁端相对于塔底的地震位移随视波速的变化曲线。由图可知：视波速减小会减小主梁地震位移，但会增大塔顶纵向位移，主缆纵向不对称布置不会改变这一规律；除了南塔顶位移外，三个模型对视波速的敏感性差别很小，梁端位移最大影响-10%左右，北塔顶位移最大影响+170%左右，而南塔顶位移的最大影响从对称模型的+167%减小为300 m模型的+128%。 不过，设防地震下桥塔保持弹性，塔顶位移不控制设计。

图4 行波效应对位移的影响

6 结 论

本文以一主跨为1560 m的悬索桥为背景，改变主缆南边跨跨径建立计算模型，研究了一致激励和行波激励下主缆纵向不对称布置对悬索桥地震反应的影响。主要结论如下：

(1)主缆纵向不对称布置主要会影响以主塔振动为主的振型周期，主缆边跨的大幅减小会小幅减小对应侧主塔的侧弯和纵弯振型周期；

(2)在一致地震激励下，主缆纵向不对称布置主要会影响主塔的纵向地震反应，主缆边跨大幅减小会明显减小对应侧塔底弯矩，增大另一侧塔底弯矩，同时显著减小塔顶位移；

(3)主缆纵向不对称布置不会改变行波效应的影响规律，但会使地震反应对视波速更为敏感；相对而言，行波效应对塔底内力的影响较小，但对塔顶位移的影响较大。