基于可靠性的混合动力公交客车高压电气系统故障分布规律研究
2022-01-12朱荣
朱 荣
(陕西工业职业技术学院汽车工程学院 陕西 咸阳 712000)
引言
由我国交通运输部于2016 年以1 号令形式颁发,并于2019 年通过第19 号令修正的《道路运输车辆技术管理规定》中强调:不但鼓励道路运输企业使用节能且环保型的车型,而且简政放权,将营运车辆的技术管理主责交还给道路运输企业本身[1]。在这种背景下,道路运输经营者积极响应政策号召投入新能源节能环保车辆运营的同时,还要考虑在不影响车辆运营时间且不提高维护和修理成本的前提下,对道路运输车辆实行正确使用、周期维护、视情修理、定期检测[2-3]。当前我国绝大多数城市投入使用的主流新能源公交是纯电动和混合动力这2 类形式的。对于城市公交客车而言,混合动力公交客车(以下简称混动公交)因具有2 套动力系统,兼顾了传统动力车辆和纯电动车辆的优点,在使用过程中驾驶员及公交运营企业反响均较纯电动公交客车好。由于混动公交的高压电气系统部分与传统动力源公交客车的结构迥异,且对其进行维护和修理需要特种作业证(高压电工证),因此对于高压电气系统部分的维护和修理目前绝大多数公交企业均严重依赖于厂家。高压电气系统的故障主要属于电子元件及电路故障,这类故障一般与车辆使用时间或行驶里程没有直接的线性关系。然而作为城市公交客车而言,使用条件基本是固定的,且车辆除了正常的修理或保养时间外,其他时间基本均处于运营状态。因此对高压电气系统的故障规律进行探究,有助于指导车辆的正确使用、周期维护和视情修理。
1 故障分布规律研究技术方案
为了指导西安市混动公交的维护与使用,在对其进行应用探究过程中[3],为摸索混动公交高压电气系统故障分布规律,提出了一套高压电气系统故障分布规律研究方案。该方案以可靠性理论为基础,采用启发式算法思维,具体技术路线如图1 所示。

图1 技术路线图
具体技术方案分为以下几步:
1)故障数据收集与整理
选择n 台同类型混动公交车辆,以故障现象和故障里程的方式,采集高压电气系统初次故障数据,共n 个。剔除非正常使用导致的m(0≤m <n)个故障数据后,将剩余的n-m 个故障数据按照故障里程数从小到大依次进行排序,记为Li,i=1,2,…,n-m。
2)故障数据分析
计算Li(i=1,2,…,n-m)时的累积分布函数的估计值Li),数学公式为:

3)选择理论分布模型
对初次故障里程处理后的数据分别进行不同的理论分布最小二乘拟合,求得回归直线图进行线性比较;并借助于最小二乘法计算相关系数后,进行相关系数大小对比。基于以上2 种方法综合选择合适的理论分布模型。
4)理论分布模型拟合检验
借助于拟合检验法来判断基于上一步选取的理论分布模型是否合格。若经过拟合检验确认不合格,则返回步骤3),进行理论分布模型的再选择。常用的分布拟合检验方法有:正态分布拟合检验法、t 拟合检验法、χ2拟合检验法、K 拟合检验法等[4]。
5)理论分布模型参数估计
确认好理论分布模型之后,借助图分析法或数值分析法估计所确认的理论分布模型的参数[5-6]。
6)故障分布函数确认
基于上述两步,求出故障分布函数,并对应地计算出概率密度函数、可靠度函数、故障率函数等。
7)可靠性指标计算
根据实际应用的需要,依据上一步计算获得的相关函数进行所需的可靠性指标计算。常用的可靠性指标主要有:可靠度、有效度、平均维修时间、平均工作时间、失效度等。
2 案例分析
以西安市40 路型号为KLQ6129GAHEV5C 的苏州金龙海格牌混动公交为研究对象,通过对高压电气系统初次故障数据进行统计与分析,以期挖掘出该车型高压电气系统故障分布规律,进而指导该公交线路上同类型车辆的维护周期修订以及维护作业内容的编排。
2.1 故障数据收集与整理
以走访调查及查询车辆维修履历的形式,搜集到西安市40 路累计共20 台混动公交高压电气系统的初次故障数据。20 个高压电气系统故障数据中没有因非正常使用而导致的故障。根据故障里程数的大小进行从小到大排序,如表1 所示。

表1 20 台混动公交车辆初次故障数据
2.2 故障数据分析
将表1 中的故障里程数据代入公式(1)中进行计算,结果如表2 所示。

表2 故障数据处理结果
2.3 理论分布模型的选择
选择常见的正态分布模型、对数正态分布模型、指数分布模型以及2 参数威布尔分布模型,利用上一步处理获取的数据分别进行最小二乘拟合,获得回归直线图,详见图2~图5。通过对比观察不同理论分布模型的回归直线图可知,服从2 参数威布尔分布的几率最大。

图2 正态分布函数回归直线图

图3 对数正态分布函数回归直线图

图4 指数分布函数回归直线图

图5 2参数威布尔分布函数回归直线图
进一步借助于excel 函数对上述4 种理论分布函数模型计算最小二乘法拟合的相关系数,计算结果详见表3。

表3 4 种理论分布模型相关系数计算结果
2.4 理论分布模型拟合检验
在上述2.3 中,借助于回归直线图进行线性分析和比较最小二乘法拟合的相关系数大小2 种方法,对4 种常见的理论分布模型进行分析,判断首次故障分布规律服从2 参数威布尔分布的可能性最大。本案例拟借助t 检验法进行2 参数威布尔分布模型假设检验,具体方案如下:以t 检验法确定临界拟合优度,再将临界拟合优度与拟合优度作大小比较,判断线性关系成立与否,进而分析假设是否成立。
拟合优度计算公式:

借助tn-2,1-a/2确认临界拟合优度:

式中:α 是t 分布的显著水平。
通过检验:r2>能否成立,进而判断y 和x 之间一元线性关系(y=ax+b)是否存在。
经计算,可求出拟合优度r2=0.977 1。因为r2=0.977 1 >0.9=,所以y 和x 之间存在一元线性关系(y=ax+b),进而说明假设成立。
2.5 理论分布模型参数估计
2 参数威布尔分布,其可靠度函数为:

式中:L 为故障里程,km;m 为形状参数;η 为尺度参数。
对上式两边取两次对数可得:
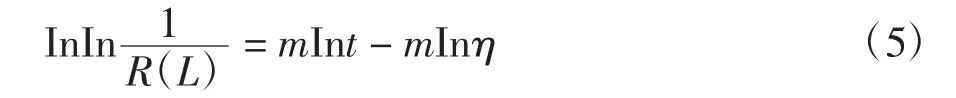
因此,对于InLi和的一组数据,可用最小二乘法拟合求得回归系数a 和b。其中a=m,b=-mInη,进而可求得威布尔分布模型的参数估计值m 和η。
通过计算,得到a≈1.454 10,b≈-15.699 12。进一步计算,得到形状参数m=1.454 10,尺度参数η≈48 847.154 21。
2.6 故障分布函数确认
将2.5 中求得的m 与η 代入2 参数威布尔分布模型中。
1)计算求得故障分布函数为:

对应函数图形如图6 所示。

图6 故障分布函数曲线图
2)计算求得概率密度函数为:
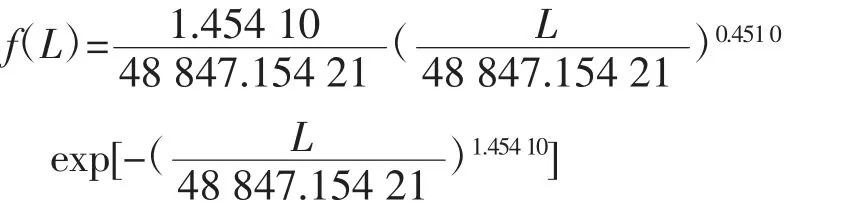
对应函数图形如图7 所示。

图7 故障概率密度函数曲线图
3)计算求得可靠度函数为:

对应函数图形如图8 所示。

图8 可靠度函数曲线图
4)计算求得故障率函数为:

对应函数图形如图9 所示。

图9 失效度函数曲线图
2.7 可靠性寿命值估计
基于可靠度函数,考虑维护周期的优化修订需要以及不同级别的维护作业内容的设计,求出混动公交高压电气系统特征寿命、平均初次故障里程、额定寿命等可靠性寿命度量指标,如表4 所示。

表4 部分可靠性寿命度量指标计算值km
3 结论
利用车辆维修履历,在剔除因非正常使用导致的故障数据后,以故障现象和故障里程的形式收集初次故障数据,并以可靠性理论为研究基础,引入启发式算法思维,提出了一套故障分布规律研究技术方案。并以西安市40 路20 辆混动公交高压电气系统为例,对所提出的的技术方案进行了验证,得出该路线混动公交高压电气系统故障服从2 参数威布尔分布,并相应地计算得出了其故障分布函数及可靠性寿命值。该技术方案具有故障数据获取方便,操作简单等特点,具有较好的实际推广价值和意义。该技术方案同样也适用于其他使用条件相对固定的道路运输车辆故障分布规律研究。不足之处在于,案例中选取的试验车辆数和故障数据相对偏少;故障分布模型选择时,只列举了常见的故障分布模型,不常见的分布模型未进行罗列。
