GRACE Follow-On卫星的星载GNSS相位测速法

刘 晗，魏 辉，邹贤才

武汉大学测绘学院，湖北 武汉 430079

随着人造地球卫星技术的不断发展，以及探测地球及宇宙空间环境的更高要求，人类发射低轨卫星的数量与日俱增。近年来，各国发射了大量低轨卫星均搭载有星载GPS接收机用于提供精密轨道信息，例如，用于反演重力场的CHAMP[1-2](CHAllenging Minisatellite Payload)、GRACE[3](Gravity Recovery and Climate Experiment)、GOCE[4](Gravity Field and Ocean Circulation Explorer)和GRACE Follow-On[5]卫星;用于监测全球海面温度和海平面高度Sentinel-3A[6-7]卫星、用于海洋测高的TOPEX/POSEIDON卫星[8]和Jason-1/2/3[9-10]卫星；用于地磁探测的SWARM[11]卫星等。

目前经典的星载GPS定轨方法有：运动学方法(kinematic method)、动力学方法(dynamic method)和简化动力学方法(reduced-dynamic method)。相比于动力学和简化动力学轨道，运动学轨道仅利用GPS几何距离观测值实现对低轨卫星的精密定轨，不包含先验重力场和力学模型信息[12]。但精密运动学轨道不可避免地会涉及整周模糊度固定问题，导致轨道解历元间存在相关性，且不能直接提供速度和加速度信息。而动力学方法和简化动力学方法或多或少受到先验重力场和力学模型的影响[13-14]，其解算出来的精密轨道会包含先验重力场信息。如果应用于纯卫星重力场解算的话，会导致最终卫星解存在一部分“污染”。利用载波相位中心差分获取多普勒观测值，精度上优于原始多普勒观测值的速度计算结果[15-16]。

文献[17]针对航空重力中载体加速度的确定，提出直接对相位观测值微分可以提高解算效率，能避免利用运动学轨道时需要先固定整周模糊度求解位置信息的问题，但其仅利用4颗卫星的观测信息。文献[18]在此方法基础上引入最小二乘算法，利用协方差矩阵给所有可用卫星数据定权，其试验结果表明精度优于位置微分法。文献[19]在现有研究的基础上，提出了EVA方法(extended velocity and acceleration determina-tion)，不再采用双差以削弱或消除卫星钟差和钟漂，而是在解算速度与加速度的同时对卫星钟差和钟漂进行估计，且仅利用协方差矩阵的主对角元素，不考虑各测量的相关性，提高了航空重力数据的处理精度。文献[20]利用GOCE卫星的星载GPS载波相位观测值，基于长度为7点的数值微分器反演地球重力场，结果表明载波微分法解算70阶以上的地球重力场系数精度高于位置差分法。以上研究表明载波相位直接差分得到速度、加速度相比于先精密定位/定轨再位置差分法而言，能削弱位置解/轨道解历元间相关性对其微分速度和加速度的影响，无须固定模糊度。

GRACE Follow-On卫星任务，作为GRACE卫星任务的后续，于2018年5月发射，由两颗同轨道面的GRACE C/D卫星构成，轨道高度约500 km，轨道倾角89.035°，偏心率0.001 79，可精细观测地球重力场及其变化[21-23]。本文将研究基于GRACE Follow-On卫星任务实测星载GPS载波相位观测值，通过数值微分方法，精确确定卫星的速度和加速度，并分析比较不同微分器、采样间隔和钟差产品等因素的影响。

1 载波相位直接法

对于低轨卫星，利用载波相位直接微分法确定卫星速度/加速度的基本公式[17-18]如下

(1)

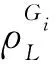
LEO卫星的GPS双频载波L1/L2相位观测方程式为

(2)

(3)

整理可得

(4)

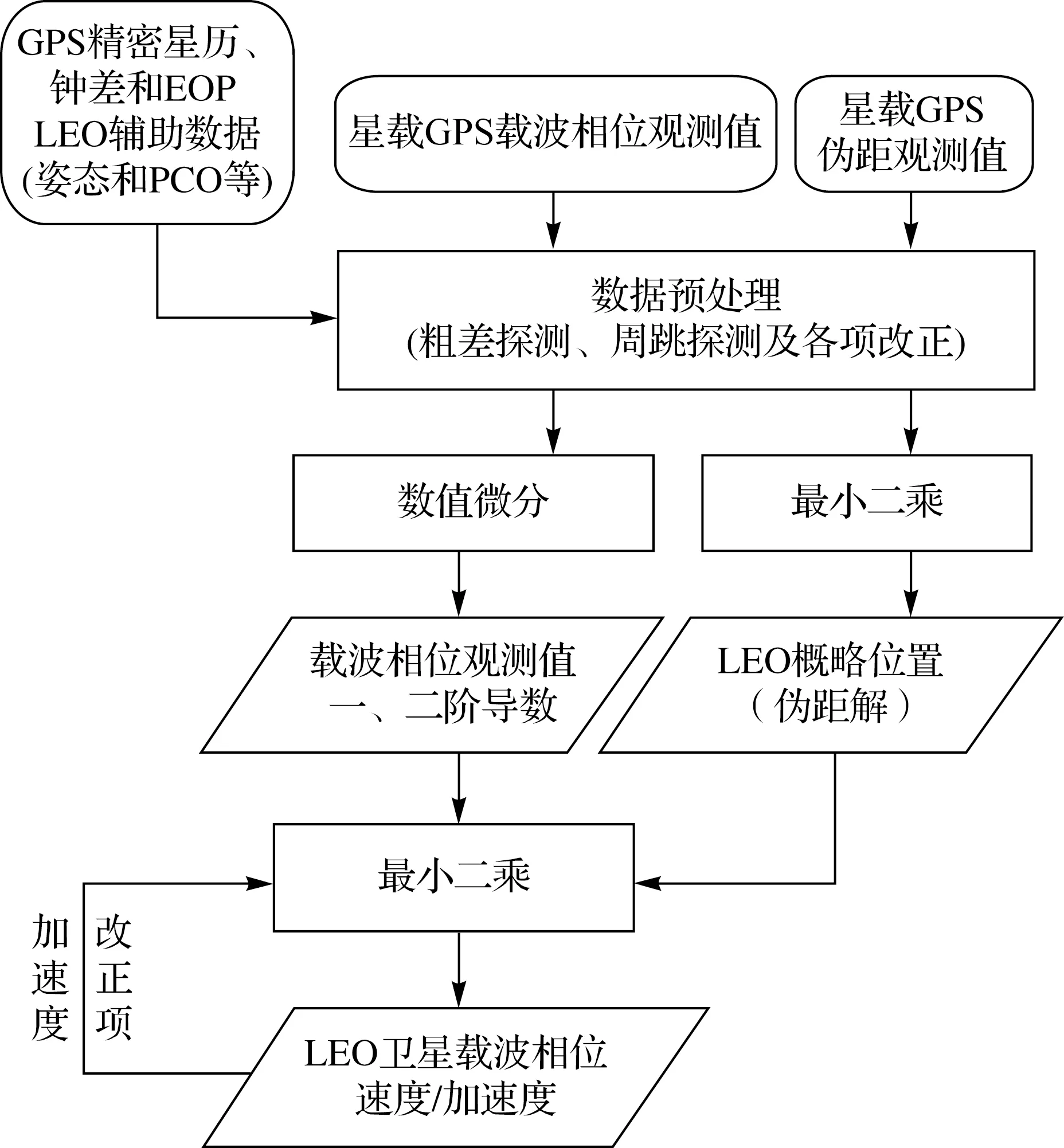
图1 低轨卫星载波相位直接法确定卫星速度和加速度流程Fig.1 Precise GPS phase velocity and acceleration determination for LEO

2 数值微分

文献[24—25]采用了泰勒级数展开、傅里叶级数滤波器、Remez变换滤波器等多种方法，对GNSS观测值的数值微分方法在不同GNSS领域里的应用进行了研究。综合以上的多种研究结果，本文采用有限脉冲响应FIR微分器，对载波相位数据进行数值微分。为方便对卫星数据的处理，通常采用奇数点长度的微分器，离散的时间序列一阶数值微分的公式可表示为

(5)

式中，hM[n]为微分器的系数，微分器长度为2M+1点。显然，经过滤波后时间序列数据存在损失问题，损失离散点数量为2M[18,25-26]，故微分器长度一般不超过9点。加速度对应的二阶数值微分器与式(5)相似，仅系数不同。不同长度不同阶次数值微分器系数见表1，其中T为数据微分间隔。

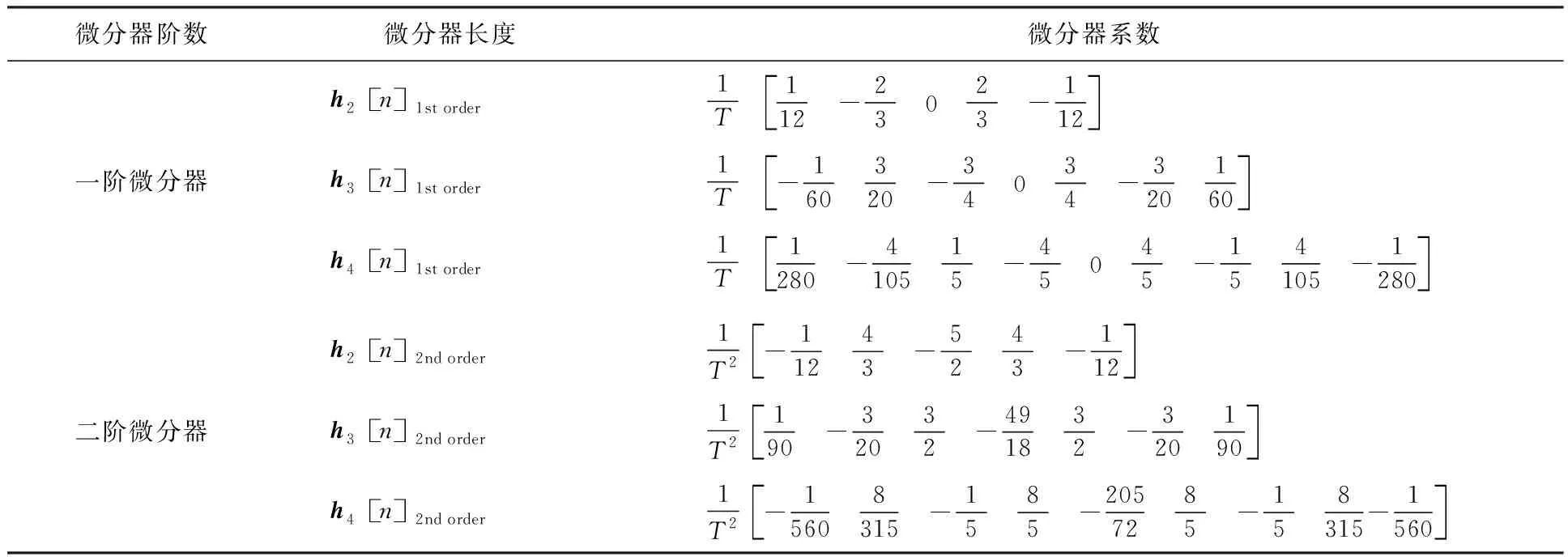
表1 FIR微分器参数

3 试验结果和分析

本文采用GRACE Follow-On 2018年11月1日至2018年11月10日的L1B数据，主要包括GPS1B观测文件、SCA1B姿态文件等，可由德国地学研究中心的ISDC(Information System and Data Center)获取。GRACE Follow-On卫星(C/D)的PCO(phase center offset)以及CoM(Center for Mass)位置参数[27]见表2。选择CODE提供的精密星历和5 s钟差产品，利用表1给出的FIR数值微分器，处理了10 d的星载GPS数据(观测值采样间隔为10 s)，进行低轨卫星载波相位直接法确定卫星速度和加速度的试验分析。

表2 GRACE Follow-On数据说明

3.1 GRACE Follow-On参数选择

为分析数值微分器参数对的载波相位直接法确定GRACE Follow-On卫星速度和加速度的影响，分别采用不同的微分间隔(T=10 s，30 s，60 s，90 s，120 s)，不同长度的数值微分器(5点，7点，9点)，设置15种不同参数方案，对GRACE C卫星和D卫星进行了试验。利用JPL(Jet Propulsion Laboratory)提供的GRACE Follow-On卫星事后简化动力学精密轨道作为“真值”进行精度评估(简化动力学轨道仅直接提供卫星速度，加速度由数值微分获取)。不同方案采用载波相位直接法确定的GRACE Follow-On卫星速度和加速度与简化动力学精密轨道差异的3D RMS见表3。结果表明，①当微分间隔大于30 s时，随着微分间隔T的增加，确定速度和加速度精度会开始降低。由表1和式(4)可知，载波相位直接法的噪声主要来自两方面，数值微分器的误差和观测噪声。随着微分间隔T的增加，能在一定程度上降低观测噪声的影响，但数值微分器的误差会随之增大。实际数据处理中需要均衡两者的影响。②相比5点微分器，7点和9点的数值微分近似精度更好，因此对较大微分间隔也能取得较好的数值微分结果。③当微分器的长度为9点，采用载波相位直接法GRACE Follow-On卫星速度(微分间隔60 s)的3D RMS最佳，可达0.227 6 mm/s(C卫星)和0.238 4 mm/s(D卫星)；确定卫星加速度(微分间隔90 s)的3D RMS最佳，可达4.1 μm/s2(C卫星)和4.5 μm/s2(D卫星)。这可能是因为卫星速度与加速度信号特征有所不同，微分器参数有着细微差异。

表3 GRACE Follow-On各参数的3D RMS统计值(观测值采样间隔10 s)

滤波器长度9点时，采用载波相位直接法得到的低轨卫星速度(微分间隔60 s)、加速度(微分间隔90 s)差异时间序列如图,由图2可知,在该组参数设置下，确定GRACE Follow-On卫星速度在轨道坐标系下R、A、C分量的STD(standard deviation)对C卫星分别为：0.190 8 mm/s、0.090 8 mm/s、0.073 8 mm/s，D卫星分别为0.197 9 mm/s、0.095 2 mm/s、0.076 1 mm/s，均在0.20 mm/s以内，差异的平均值可忽略；载波相位直接法得到的加速度R、A、C分量的STD对C卫星分别为：3.191 0 μm/s2、1.998 9 μm/s2、1.163 1 μm/s2，D卫星分别为3.436 9 μm/s2、2.178 0 μm/s2、1.264 5 μm/s2，差异均在3.2 μm/s2以内，差异的平均值可忽略。与GRACE Follow-On事后精密简化动力学轨道解符合很好。

图2 GRACE Follow-On C/D卫星速度(60 s, 9点)和加速度(90 s, 9点)残差图Fig.2 Residuals of GRACE Follow-On C/D velocity (interval=60 s, M=4) and acceleration (interval=90 s, M=4) determination using FIR filter

速度和加速度残差的纬度分布如图3所示。本文确定的GRACE Follow-On卫星速度和加速度在高纬度区域精度较差，近两极地区和赤道附近数据较少。这可能是因为在相应区域载波数据观测精度较差和周跳较多引起的，因此图2时间序列的残差也表现出一定周期性“特征”。在某些区域(尤其是赤道附近)，加速度数据少于速度数据，这是数值微分过程引起的损失，微分间隔越大数据损失越多。

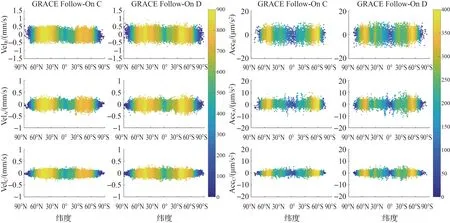
图3 GRACE Follow-On C/D速度(60 s, 9点)和加速度残差(90 s, 9点)的纬度分布Fig.3 GRACE Follow-On latitude distribution of C/D velocity (interval=60 s, M=4) and acceleration (interval=90 s, M=4) residuals

需要指出的是，采用较大微分间隔(如60 s、90 s)确定速度和加速度精度较好，此时数据损失也较严重，尤其是当周跳较多时。但对低轨卫星来说，该方法仍然能在不需要固定整周模糊度，不引入卫星动力学模型的前提下，提供大量的“额外”观测数据，为GRACE Follow-On任务的精密定轨和重力场解算提供高精度的速度和加速度信息。

3.2 钟差产品

GOCE卫星精密定轨的研究表明发现高频的GPS钟差改正产品有利于提高定轨精度[28-29]。基于此，本文比较了CODE机构的5 s钟差产品和IGS 30 s钟差对GRACE Follow-On卫星载波相位直接法确定速度和加速度的影响。

对比使用不同的钟差产品得到的3D RMS如图4所示，结果表明：①对于观测值采样间隔为10 s的情况而言，使用30 s的钟差产品相较于使用5 s的钟差产品，由载波相位直接法得到的低轨卫星速度和加速度精度变差，与GOCE的研究结果类似；②不同频率钟差产品之间的差异随着FIR滤波器微分间隔的增大而减小，由于此差异量级较小在微分间隔过大时会被数值微分器自身的误差“淹没”。

图4 使用不同微分器参数的解算结果对比Fig.4 Velocity and acceleration 3D RMS comparison between 30 s IGS clock corrections and 5 s CODE clock corrections (observation sampled at 10 s)

3.3 降采样

为进一步分析钟差产品对结果的影响，对星载GPS观测值进行降采样为30 s，使用CODE 05 s钟差与使用IGS 30 s钟差进行比较，结果见表4。当滤波器参数一定时，观测值采样间隔大于等于钟差产品间隔(30 s)时，CODE 05 s钟差与使用IGS 30 s钟差结果相当。结合3.2节的结果，这表明对GRACE Follow-On卫星而言，钟差产品的影响主要来自数据处理中GPS钟差改正的影响，数据采样间隔10 s时，对于IGS 30 s钟差产品，其钟差改正需采用30 s数据内插，精度较CODE 05 s产品差。GRACE Follow-On卫星实际数据处理时需要考虑这部分因素的影响。采样间隔较大时，不同钟差产品的精度相当，说明不同机构提供的GPS精密星历和钟差产品之间存在较好的一致性和内部自洽性。

表4 对星载观测值降采样时使用不同频率钟差产品的低轨卫星解算结果

4 结 论

载波相位直接法确定卫星速度和加速度相比于先运动学定轨再差分的方法而言，削弱了轨道历元间相关性对其微分速度和加速度的影响，无须固定模糊度。本文从低轨卫星的星载GPS载波相位观测数据出发，研究了不同微分间隔、不同FIR微分器、不同钟差产品，载波相位直接法确定GRACE Follow-On卫星速度和加速度的最优策略，结果表明：

(1) 当微分器长度设置为9点时，GRACE Follow-On C/D卫星速度精度(微分间隔=60 s)3D RMS可达0.227 6 mm/s、0.291 9 mm/s；加速度速度精度(微分间隔=90 s)3D RMS可达4.1 μm/s2和4.5 μm/s2。

(2) 对于10 s采样的GRACE Follow-On卫星数据，CODE 5 s钟差产品的精度优于IGS 30 s，当降采样为30 s时，两者精度相当，实际数据处理时需考虑该因素的影响。

尽管在周跳较多的情况下，载波相位直接法微分速度和加速度的数据会有大量缺失，但是对低轨卫星来说，这部分观测值依旧能在不需要固定整周模糊度，不引入卫星动力学模型的前提下，提供大量的“额外”观测数据，为GRACE Follow-On任务的精密定轨和重力场解算提供高精度的速度和加速度信息。