GNSS多径信号3种非监督学习法分析与比较

朱 彬，杨 诚，刘 岩

中国地质大学(北京)土地科学技术学院，北京 100089

全球导航卫星系统(GNSS)的精确定位需要满足接收机与卫星之间的通视，即获得视线信号(LOS)。在城市复杂环境下，由于高架路、天桥、楼房等建筑物对卫星信号的遮挡，易形成多路径效应，接收机经常无法接收到视线信号，却只能接收非视线信号(NLOS)，严重影响GNSS的定位精度[1-2]。研究结果表明，多路径信号误差一般为几米，而NLOS的误差可达到数十米甚至上百米[3-5]。有学者将多路径和NLOS信号统称为多径信号[6]。

削弱GNSS多径误差的影响可以从GNSS天线、接收机、数据后处理等多方面着手。在硬件方面，可以使用延迟锁定环(DLL)技术抑制多路径效应的影响[7]。文献[8]基于GPS信号多径模型的特点，利用信号分离法估计GPS信号的频率和时间延迟。在仿真结果中，该方法能够有效地抑制多径信号。文献[9]利用软件接收机分离NLOS信号和LOS信号成分，可以提高定位精度。在天线方面，可以利用双极化天线有效减弱多路径和NLOS信号的影响[10]。但是天线设计成本昂贵，低成本接收机很难实现。

在数据后处理方面，通过对观测信息的合理定权，例如伪距观测值、载波观测值、多普勒频移赋以不同的权，或利用信噪比以及高度角等参数调整削弱多径对定位结果的影响[11-13]；然而，在城市复杂区域，这些方法改善定位精度的效果并不显著[14]。文献[3，15—16]通过跳变马尔可夫系统对伪距误差建模，并利用一致性检验等方法减弱多径误差对伪距定位的影响。

利用惯性传感器辅助GNSS进行组合定位也可以降低多径误差的影响。组合系统利用惯性传感器不受环境影响的优势，可以提高组合系统定位精度[17-19]。然而，惯性导航系统的精度与成本成正比，限制了组合系统的广泛使用。

近年来，智能学习在GNSS多径误差识别方面得到广泛关注，主要方法为监督学习和非监督学习。监督学习通过训练标记的样本得到一个最优模型，从而进行分类。例如支持向量机(SVM)、k-最近邻算法(KNN)、随机森林(RF)、决策树(DT)等。SVM是按监督学习方式对数据进行二元分类的广义线性分类器。利用SVM算法对GNSS接收的原始观测值进行分类，可将LOS与NLOS信号相区分[20]。KNN算法通过识别样本临近的k个最近样本的类别，从而判断该样本的从属类别。监督学习在城市三维模型的阴影匹配方面应用效果较好[16,21-23]。但是，该算法在提高城市峡谷中的定位精度的同时，也增加了计算的复杂性和计算负荷。

与监督学习相反，非监督学习不需要对样本进行标记，通过对数据进行挖掘，检测数据中的异常值。目前非监督学习已经广泛应用于数据挖掘、模式识别、图像分析以及计算机视觉等领域。在GNSS数据处理方面，非监督学习法也显示出更灵活和更智能的优点。利用非监督学习法可以把GNSS信号的误差进行聚类，进而控制其影响。如果非监督学习法能合理将GNSS多路径信号和NLOS信号与LOS信号进行聚类，则很容易隔离其影响，提高复杂环境下GNSS定位精度。在非监督学习中，k均值聚类算法(k-means)是常用聚类分析算法，该算法的核心是要求同一类样本与聚类中心的欧氏距离的平方和最小。显然，该聚类法的初始聚类中心十分重要，如果初始聚类中心选择精确，则k-means聚类效果就会很好。通常初始聚类中心随机选取，受异常点的影响较大，因此有学者提出改进的k-means++方法[24]。采用k-means++聚类法，可有效分离LOS与多径信号[25]。也有学者采用高斯混合聚类(GMM)判断单个样本在不同分类中的概率，进而实现样本的分类[26-27]。该方法也可以用于双频模糊度估计，减少多径误差影响[28]。此外，模糊c-均值聚类(FCM)法也是一种常用的方法，该方法基于对目标函数优化进行聚类，已经被应用于惯性系统载体运动阶段的聚类[29]。

综上所述，随着机器学习的应用，传统的GNSS多路径和NLOS信号的处理模式逐渐向着机器智能处理方向发展，呈现出了较高时效性和智能化水平[30-31]。非监督学习避免烦琐的GNSS数据预处理，又可以提高定位精度。笔者使用3种非监督学习算法对GNSS信号进行智能化聚类，旨在提高低成本接收机在复杂环境下的定位精度。

1 GNSS数据分类特征

GNSS的原始观测值包括伪距、载波相位和多普勒频移等，这些原始观测参数可以作为机器学习的特征值。GNSS的伪距观测残差和伪距率一致性也是有效的特征值。

为了提高多径误差的分类精度和效率，常采用不同的特征值组合[1]。本文使用4个主要特征。

(1) 信噪比(SNR)：信噪比是判别LOS和NLOS的常用变量。在大多数情况下，多径信号的反射和折射会降低信号强度。信噪比可以从GNSS观测文件中获得。

(2) 伪距残差：伪距观测残差反映了观测值的精确度，所以伪距残差也可作为分离LOS和NLOS的特征变量。

(3) 高度角：在城市环境中，具有较高仰角的卫星信号一般不易被周围建筑物遮挡，但是容易出现NLOS误差影响；较低仰角的卫星信号容易被建筑物遮挡，出现LOS受阻的情况。因此可以采用高度角作为检测NLOS的特征值。如上所述，单独依赖卫星高度角很难有效地识别NLOS，一般需要组合其他特征值进行综合检测[32]。

(4) 伪距率一致性：伪距率是两个历元之间接收机对同一颗卫星观测的伪距测量的变化率，表示为

(1)

(2)

(3)

式中，Ω为伪距率的差值，需要注意的是，伪距率一致性是以伪距变化率为参考，因为伪距变化率受多径影响相对较小。

由于4个特征值对于多路径和NLOS都具有不确定性，并且相互之间有联系，因此可以采用4个特征值的组合识别多径误差。为了消除不同量纲对聚类结果的影响，需要进行数据标准化处理，使得各指标处于同一数量级，便于分析。本文使用归一化对数据进行处理

(4)

式中，Z*为样本数据归一化后的值；Z为样本数据；Zmax为样本数据的最大值；Zmin为样本数据的最小值。

2 GNSS信号聚类算法

2.1 最佳聚类数目

复杂环境下，为了确保信号分类数量k的最优性，可以使用Calinski-Harabasz(CH)指标检验最优的k值[33]

(5)

式中，CH(k)为CH指数；Bk为集群之间的协方差；tr(·)为矩阵的迹；n为样本总数；k为聚类中心个数；Wk为集群内部数据的协方差。当样本总数和聚类中心个数一定时，类自身越紧密，聚类效果越好。在样本充足的情况下，只要合理选择GNSS数据中的特征向量，CH指标的判断将会很精确。

2.2 k-means++聚类

训练集中的每个样本表示为X={x1,x2,…,xi},i=1,2,…,n，其中参数xi={ci,ρi,eli,Ωi}为标准化载噪比ci，伪距残差ρi，卫星高度角eli以及伪距率一致性Ωi所组成的特征样本，n为整个观测期间的样本总数。假设存在m个聚类中心，聚类中心特征样本为N1、N2…Nm(即质心)，k-means++依据轮盘法使初始聚类中心之间的相互距离尽可能远，再将每个样本点划分到距离质心最近的簇中，通过欧氏距离进行计算，即[34]

(6)

由于质心参数可能存在较大的误差，导致聚类结果较差，需要进行迭代重新计算质心，即

(7)

当每个簇内的样本与质心的误差平方和变化微小，迭代即可停止，误差平方和可以表示为

(8)

基于k-means++的GNSS信号分类算法流程如图1所示。

图1 k-means++流程Fig.1 k-means++ flow chart

2.3 高斯混合聚类(GMM)

高斯混合聚类也是通过样本的训练对目标进行分类。本文中，该算法采用与k-means++相同样本，X={x1,x2,…xi}。GMM由m个高斯概率密度叠加，表达式为[35]

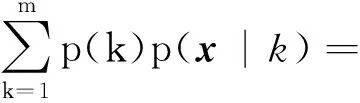
(9)

式中，N(x|μk,Σk)是第k个分类模型的高斯分布；μk为每个类的均值；Σk为协方差矩阵；πk为混合系数，即每个高斯分布对样本的影响因子，其和为1。对于每一个样本数据x，高斯分布的概率密度函数表达式为

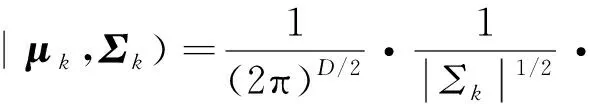
(10)

式中，D是样本的维度。要获得一组混合系数πk、均值μk和协方差Σk的值，可以通过似然函数进行求解。

多个独立事件的边缘概率相乘可得到联合概率。因为每一个样本x独立且符合高斯分布，因此高斯混合模型似然函数表达式为

(11)

式中，N为高斯模型个数。

求解最大似然函数一般采用最大期望(EM)算法。EM算法是一种从不完全数据或有数据丢失的数据集中，求解概率模型参数的最大似然估计方法。该算法首先利用隐含变量的现有估计值，计算其最大似然估计值；然后用求得的最大似然值计算参数估值；最后进行迭代直到收敛。主要过程如下[26]:

(1) 对于每个样本xi，它由第k个高斯模型生成的概率为

(12)

(2) 参数估值μk、Σk和πk的求解结果为

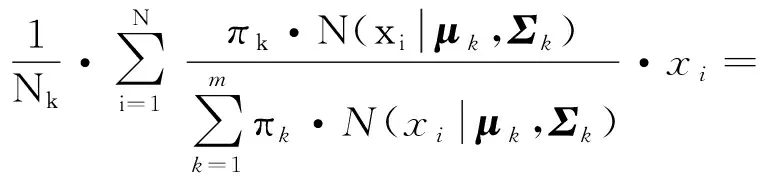
(13)

(14)

(15)

(3) 重复迭代步骤(1)和步骤(2)，每次迭代会得到新的μ,Σ和πk，求最优参数即是聚类的过程，直到各估值收敛。

基于GMM的GNSS信号分类算法流程如图2所示。

图2 高斯混合聚类流程Fig.2 GMM flow chart

2.4 模糊c-均值聚类(FCM)

已知特征数据集X={x1,x2,…,xi},i=1,2,…,n；第i个聚类中心的特征值为vi。FCM的目标函数定义为[36]

(16)

式中，uij∈[0,1]，表示第j个样本相对于第i个类的隶属度，每个样本与类的隶属度构成了隶属度矩阵U；m是聚类数目；a是一个加权指数。

隶属度须满足约束条件

(17)

即一个样本属于所有类的隶属度之和要为1。因此，构建目标函数为

(18)

求极值后得到

(19)

令dij=(xj-vi)2，再利用式(19)对隶属度函数uij求导，解得

(20)

FCM思路是通过不断更新隶属度矩阵与聚类中心，并且每次迭代计算相应的目标函数JFCM，使其达到最小值。具体步骤如图3所示。

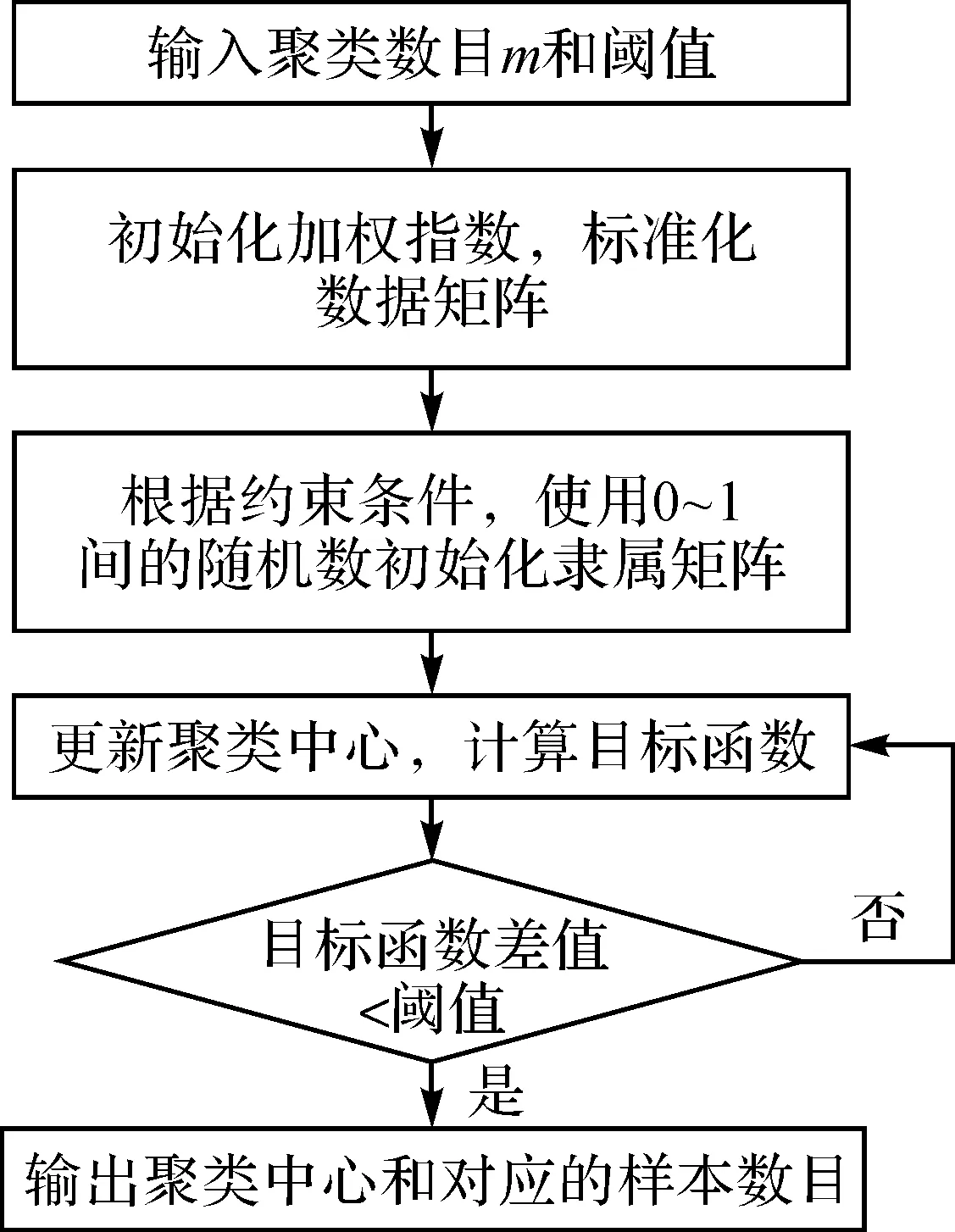
图3 模糊c-均值聚类流程Fig.3 Fuzzy c-means clustering

2.5 轮廓系数

当真实标记结果未知时，可以选择轮廓系数作为聚类性能的评估指标。轮廓系数取值范围为[-1,1]，取值越接近1，聚类性能越好。接近0的值表示重叠的群集。负值通常表示样本错误的聚类。每个样本的轮廓系数S为[37]

(21)

式中，a(i)为某个样本与其所在簇内其他样本的平均距离，体现凝聚度；b(i)为某个样本与其他簇样本的平均距离，体现分离度；聚类总的轮廓系数SC为

(22)

3 试验结果与分析

3.1 静态数据分析

试验地点为中国地质大学(北京)教一楼小花园，如图4(a)所示。本次试验采用UbloxF9p板卡的接收机采集GPS与BDS的观测数据。天线的真实坐标已知。观测时间为2020年11月15日14：00—17：00，时长为3 h，采样频率为1 Hz。周围有高楼和树木遮挡，因此天线除了接收到LOS信号外，还接收到NLOS和多路径信号，天空图如图4(b)所示。

图4 试验场地与NLOS天空图Fig.4 Experimental site and NLOS skyplot

3.2 观测质量分析

通过观测卫星数和DOP值对观测数据质量进行分析，卫星数和PDOP如图5所示。

图5中横坐标为观测历元，纵坐标为卫星数和PDOP，观测卫星数不稳定，卫星数集中在14—15颗之间，PDOP大部分在1.6～2之间。

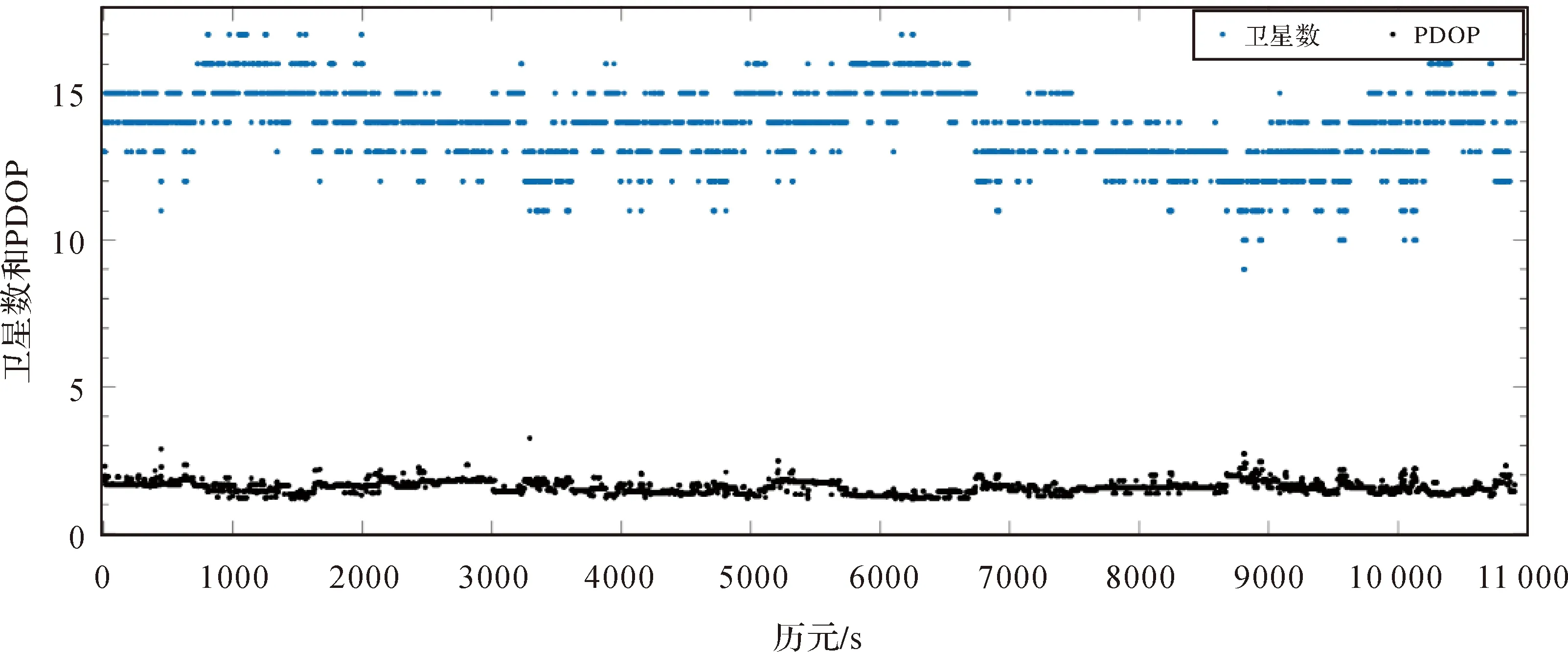
图5 卫星数和PDOPFig.5 satellites number and PDOP

伪距多路径误差的计算依赖于双频观测值，对伪距观测方程和载波相位观测方程进行组合，使用Saastamoinen模型和Klobuchar模型分别消除对流层延迟和电离层延迟消除对流层延迟和电离层延迟[38-39]，忽略载波相位多路径误差，从而计算获得伪距多路径信息，计算公式为

(23)

式中，fi、fj分别为i和j频点对应的频率值；MPi、MPj为i和j频点对应的伪距多路径误差；Pi、Pj为相应伪距观测值；Φi、Φj分别为i、j频点载波相位观测值。

通过高度角和信噪比对多路径误差进行分析，伪距多路径误差如图6所示。

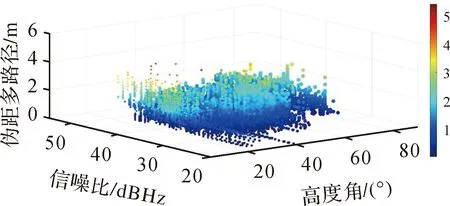
图6 伪距多路径误差与信噪比和高度角的关系Fig.6 Relationship among pseudorange multipath error, SNR and elevation angle

横坐标为高度角和信号的信噪比，右侧颜色卡为伪距多路径误差，不同颜色代表不同伪距多路径大小，颜色越红，代表伪距多路径误差越大。图6中低高度角和低信噪比区域伪距多路径大部分大于1 m，右后方高高度角和高信噪比区域伪距多路径大部分小于0.5 m。

3.3 聚类结果分析

将获取的特征值高度角、载噪比、伪距残差和伪距率一致性作为样本学习的特征向量，总样本(每个历元的可见卫星数×总历元)为157 700。4个特征值中每一个特征对判断NLOS和多路径都具有不确定性，因此采用不同特征值的组合来识别NLOS和多路径信号。为了消除不同量纲对聚类结果的影响，对数据进行标准化。使用CH指标来判断分类K值，CH指标如图7所示。

图7 不同聚类数的CH指标Fig.7 CH indexes of different cluster numbers

图7中横坐标为聚类簇数，纵坐标为CH值。当k=3时，CH的值最大，表明观测样本的聚类数为3时最佳，对应接收机接收到的3种不同卫星信号，LOS、多路径和NLOS信号与实际情况相符。

利用k-means++、GMM和FCM 3种方法进行聚类，各种信号的占比见表1。

表1 3种方法聚类结果

由表1可知，3种方法中k-means++和FCM聚类结果比较一致，而GMM聚类结果中NLOS的占比远小于其他两种方法，可能存在误聚类。利用3种方法的聚类结果，计算轮廓系数，前80 000个样本的轮廓系数如图8所示，总的轮廓系数值见表2。

图8 样本轮廓系数Fig.8 Contour coefficient of samples

表2 3种方法总轮廓系数

由图8可知，k-means++和FCM的轮廓系数大部分为正值，而GMM的轮廓系数大部分为负值并且波动比较大，说明GMM聚类结果较差。由表2可知，3种聚类方法中FCM的总轮廓系数最高，聚类性能优于其他两种方法。k-means++和FCM两者总轮廓系数比较接近，接近于1，而GMM总轮廓系数为负值，聚类性能低于其他两种方法。

3.4 定位结果分析

卫星定位精度与观测量的质量及卫星几何分布有着密切的关系，剔除NLOS数据后，参与解算的可见卫星数会减少，位置精度衰减因子(PDOP)会相应增大。但是使用GPS/BDS进行定位，通常有足够的可用卫星数，可以剔除较差的观测数据来提高定位精度。3种方法剔除NLOS卫星前后如图9所示。

由图9可以得到3种方法剔除NLOS卫星后，大部分历元都能有5颗以上卫星，能进行有效定位。由表2可知FCM方法对NLOS聚类精度最高，所以大部分历元都剔除了NLOS卫星。为了验证3种聚类方法的有效性，剔除NLOS信号后，重新进行GPS/BDS伪距单点定位，前6000历元的定位误差如图10—图12所示。

图9 3种方法剔除NLOS前后卫星数量Fig.9 Satellites number before and after the three cluster methods applied

由图10—图12可以看出，剔除NLOS信号后，东、北、天3个方向的定位精度都得到了明显的改善，只有个别历元的定位精度有所下降，可能与剔除NLOS后卫星几何分布变差有关，也可能与NLOS聚类错误有关。定位试验的均方根误差见表3。

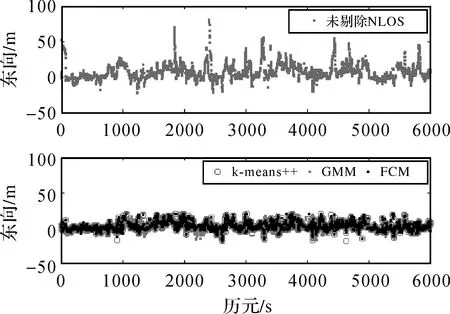
图10 东向剔除前后误差Fig.10 Error before and after elimination in East component

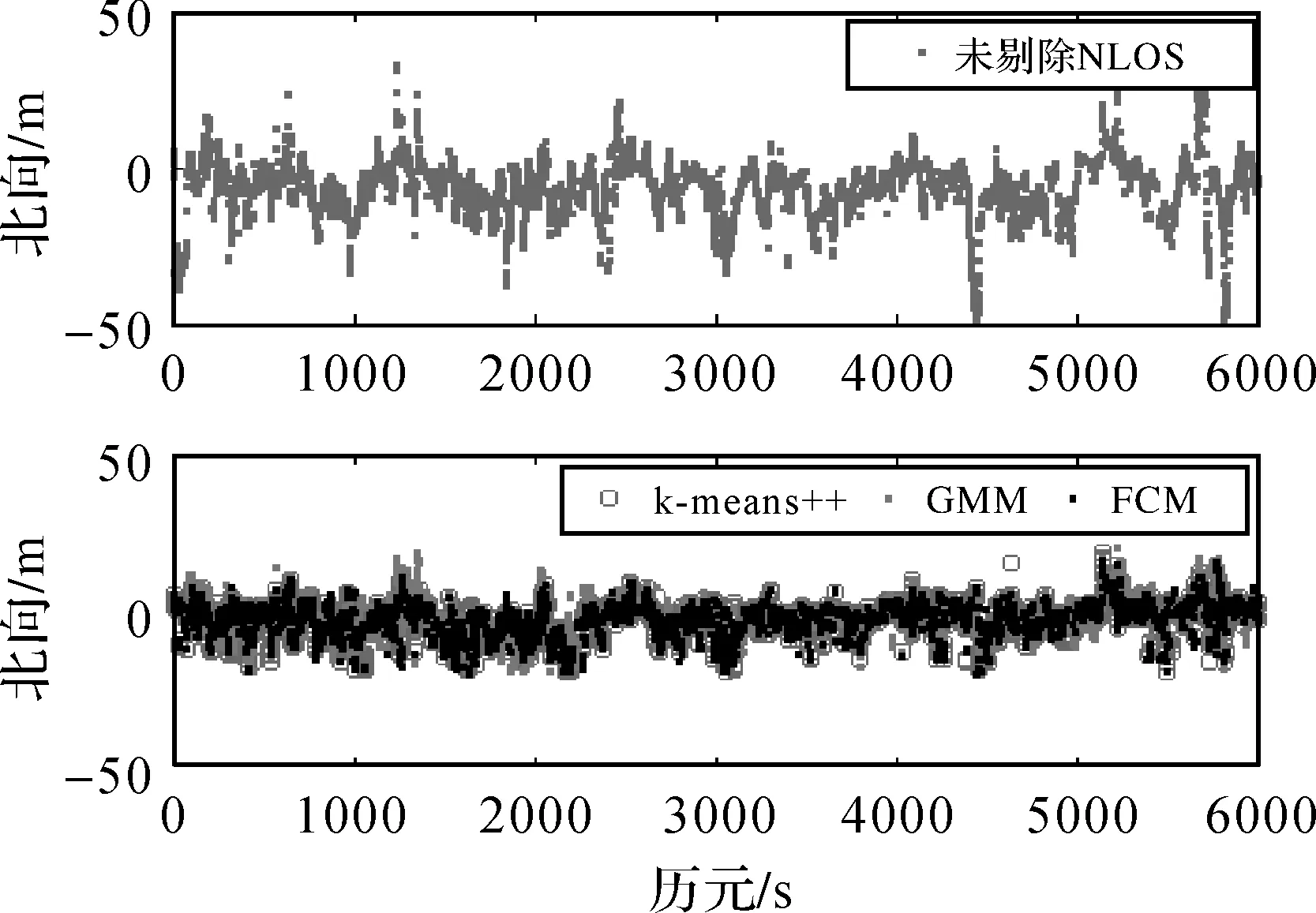
图11 北向剔除前后误差Fig.11 Error before and after elimination in North component

图12 天向剔除前后误差Fig.12 Error before and after elimination in Up component

由表3可以看出，3种方法的东北天3个方向的精度都有较显著提高，东向精度提升最高为53.9%，最低为43.5%；北向精度提升最高为51.0%，最低为40.2%；天向精度提升最高为53.1%，最低为37.9%。

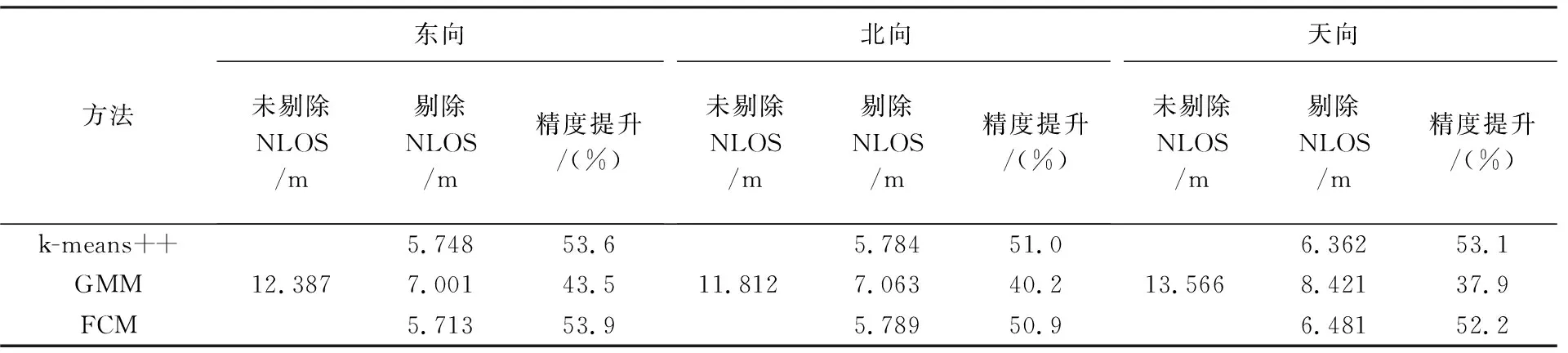
表3 剔除NLOS信号前后的伪距定位的RMSE

4 结 论

本文采用3种非监督学习法智能化控制GNSS多径误差对定位精度的影响，并通过使用信噪比、高度角、伪距残差和伪距率一致性特征值对测站的观测数据进行聚类，均取得较好的抑制多径误差影响的效果。主要结论如下：

(1) 利用建筑物边界数据得到了NLOS的天空图，发现测站周围建筑物遮挡比较严重。相比于监督学习，非监督学习法无须利用三维模型对GNSS信号进行真实标记，无须其他先验约束，显著降低了运算负荷。

(2) 3种非监督智能学习方法(k-means++、GMM和FCM)分别利用欧氏距离，概率分布和隶属程度对GNSS信号进行有效聚类。通过轮廓系数分析，k-means++和FCM两者聚类性能接近，而GMM聚类性能相对较差。

(3) 3种方法剔除NLOS信号后，东北天3个方向的精度提升约为40%～50%，其中FCM方法中的东向定位精度提高最显著，GMM方法中的天向精度提高程度不如其他分量。

本文探讨智能学习在GNSS多径信号识别与影响控制方面的应用，3种智能学习法均可用于复杂环境下GNSS实时导航定位，可有效控制多径误差对导航定位精度的影响。未来还应将三维建筑模型和射线追踪相结合，实现对GNSS信号的合理标记，并进一步分析非监督学习法对多径信号聚类效果；此外，需要继续研究不同动态环境对聚类性能的影响，研究利用非监督学习对动态特征值进行训练，以便能进一步提升多径信号识别效果。