基于深度学习的疏密条纹分类去噪分析

龚渠，张伟，王生怀，张俊杰

（湖北汽车工业学院 机械工程学院，湖北 十堰 442002）

数字条纹轮廓技术是非接触式三维形貌重建技术［1］，广泛应用于工业制造与检测、逆向设计、医疗工程等领域。数字条纹轮廓技术是采用特殊设计的结构光条纹投影到被测物体表面，然后通过提取受到被测物调制的变形条纹的信息获取物体的三维形貌。实际测量应用中，条纹图不可避免地产生噪声，影响测量精度，对条纹图进行分析之前，消除或减小噪声很有必要。简单常用的条纹图去噪算法是均值滤波和中值滤波，但会造成条纹图边缘模糊，特别是高密度条纹图边缘模糊严重，影响条纹图信息提取。旋滤波算法［2］、基于偏微分方程的条纹图去噪算法［3］等空间域滤波算法简单，处理速度快，但处理条纹图的高频信息时，会丢失图像信息造成图像模糊。傅里叶变换法［4］、小波变换［5］、窗口傅里叶变换［6］等变换域滤波能较好地抑制噪声，同时保留图像中的高频信息，但计算速度较慢。基于奇异值分解去噪算法［7］效果较好但十分耗时。非局部均值［8］用于条纹图去噪，效果好但时间较长，为了提升去噪效率只能降低去噪性能。近些年，随着计算机硬件的提升，深度学习技术快速发展，基于深度学习的条纹图去噪算法也在快速发展。Yan等［9］使用深度学习对条纹图去噪，能够得到高质量的条纹图且处理速度快。Lin等［10］提出了基于多阶段卷积网络的条纹图去噪算法，使用了3个阶段，每个阶段经过8个卷积层后得到1个噪声图像，3个阶段后对噪声图像去噪，采用较少使用的Leaky ReLU激活函数，比ReLU激活函数得到了更好的去噪性能。在实际基于条纹的测量中，不同形面会产生条纹图分布密集稀疏现象。条纹密度越高，测量精度越高，同时边缘特征越易受到噪声污染，显然密集条纹图的噪声更影响测量结果。传统条纹图滤波处理时易导致密集条纹严重模糊，导致测量结果误差较大或错误的测量结果；滤波处理后能得到高质量的条纹图，但处理时间较长。因此提出基于深度学习的疏密条纹分类去噪算法，将条纹图分为密集条纹和稀疏条纹进行处理。对比不同条纹密度类型运行时间和去噪性能，选取适当的深度学习模型参数，提高网络运算速度，同时尽可能增加去噪性能。

1 模型算法

被测物形状如图1所示，投影正弦条纹图受被测物形状调制变形。图2为不同形面调制后的条纹图。条纹图模型为

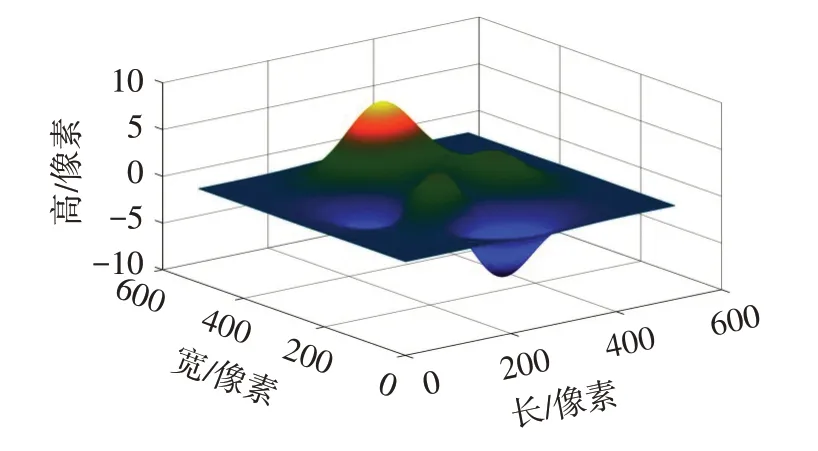
图1 被测物体的形面

图2 条纹类型

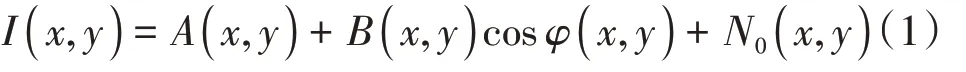
式中：（x,y）为时空坐标；A（x,y）为背景强度；B（x,y）为条纹幅度；φ（x,y）为相位分布；N0（x,y）为图像噪声。条纹图去噪目的是从噪声图像I（x,y）中去除噪声N0（x,y）。条纹投影到被测物体，受到被测物体形面调制变形，公式为

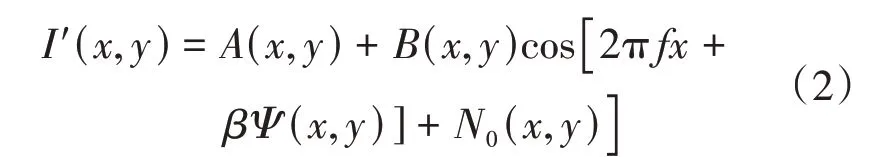
式中：f为条纹频率；β为被测物梯度系数；Ψ（x,y）为被测物形面参数。f、β与条纹密度成正比。用像素尺寸为64×64窗口提取条纹图区域中心线，依据中心线数量判定疏密类型。选取部分条纹图用上述方法提取中心线，发现稀疏条纹图窗口提取中心线数量均小于6，密集条纹图窗口提取中心线数量大于6。若某窗口提取中心线数量超过6，则判定为密集条纹图，反之为稀疏条纹图。条纹图深度学习模型去噪处理过程如图3所示。

图3 去噪处理过程

1.1 网络结构

疏密分类模型首层采用卷积连接，并用多个相同的卷积核获取图像浅层特征，卷积核参数为长、宽和通道数。通常采用长×宽像素尺寸为1×1，3×3，5×5的卷积核，尺寸选择均为奇数，是为了确保有1个中心，卷积核增大，特征信息会更丰富，然而训练速度会变慢，因此选择像素尺寸为3×3的卷积核对条纹进行训练。首先输入添加了高斯噪声的条纹图，将条纹图根据密度分类后分别放入卷积神经网络中，经过卷积神经网络后得到1个估计噪声，用噪声条纹图减去估计噪声输出得到去噪图像。卷积神经网络结构如图4所示：1）第1层L1包含了卷积滤波和ReLU（rectified linear unit）激活函数［11］，卷积滤波器个数为64，像素尺寸为3×3×1，可以输出64个特征图；2）中间层L2～Ln-1包含了卷积滤波器、批标准化（batch normalization,BN）［12］和激活函数ReLU，滤波器个数为64，像素尺寸为3×3×64；3）最后层Ln包含了1个卷积滤波器，滤波器个数为1，像素尺寸为3×3×64。

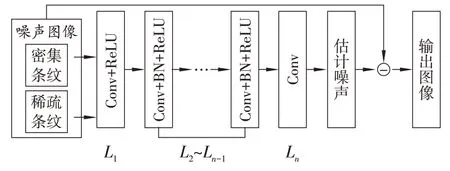
图4 卷积神经网络结构

第1层卷积是为了进行特征提取；中间层卷积后加入BN是解决内部协变量转移（internal covariate shift,ICS）问题，即神经网络后面的网络层会因为前面网络层的输入变化而变化，且变化幅度剧烈，使得学习率过低；最后层经过卷积后输出估计噪声。整个网络中每层的通道数均为64，残差模块可以直接在2个卷积层之间进行运算。残差模块和批标准化结合不仅可以加速和稳定训练过程，还能提升去噪效果［13］。

1.2 数学原理

训练网络每层的目标是解决1阶可训练非线性反应扩散（trainable nonlinear reaction diffusion,TNRD）问题［14］，TNRD的目标是解决问题：

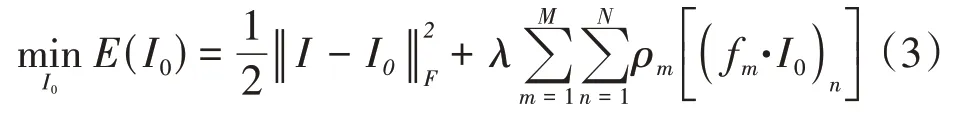
式中：I为带噪声条纹图；I0为干净条纹图；N为图像尺寸；λ为正则项系数，fm·I0为图像I0在第m次的卷积核fm的卷积；ρm为第m层的惩罚函数。式（3）的解表示从初始点I开始进行1次梯度下降：

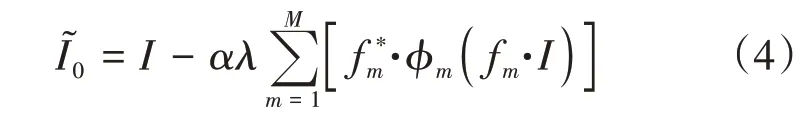
式中：fm*为fm的伴随卷积核，由卷积核fm旋转180°得到；α为步长；ϕm为影响函数。

式（4）可以等价于

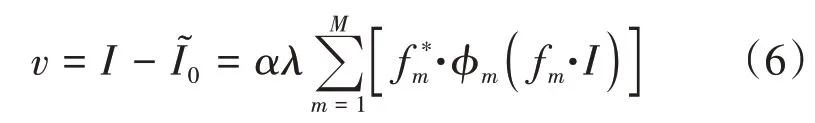
式中：v为I0对于I的估计残差。ϕm是非线性逐点映射到卷积特征图，所以式（6）实际上是2层前馈的卷积神经网络。把采用残差学习公式训练的残差图像定义为

式中：θ为网络的训练参数，包含每层训练后更新的滤波器和批标准化的参数。由此得到去除噪声的条纹图像：

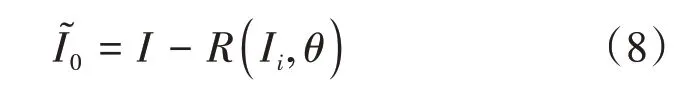
其损失函数为

式中：K为每层网络中每次训练中批次样本数量。最终训练得到高度非线性方程，作为近似的噪声强度统计分布。

2 实验结果与分析

2.1 网络训练

2.1.1 训练和测试数据

使用MATLAB随机生成10050张像素尺寸为512×512的密集条纹图和10050张像素尺寸为512×512的稀疏条纹图。将条纹图灰度化处理后，20000张图片作为训练数据，剩余100张用作检测。训练数据需要添加噪声作为输入图像，添加的噪声为高斯白噪声，其标准差σ分别为15、25和50。实验在64位Windows10系统的PyCharm社区版软件中运行，使用PyTorch深度学习框架进行网络训练，电脑硬件配置为Intel Core i5-9700CPU 3.00GHz，显卡为NVIDIA GeForce GTX1660Ti。

2.1.2 参数设置

为了探究卷积层数对不同密度条纹图的去噪效果，多次实验发现，卷积层数设置为7和17的效果较好，选择Adam（adaptive moment estimation）参数优化法，权值更新如下：

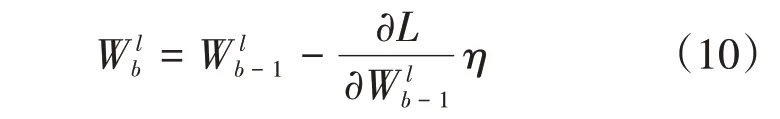
式中：W为卷积核权值；l为第几层卷积；b为迭代次数；η为学习率，设为0.0001。批标准设为128，W初始化为均值0、标准差0.001 的正态分布。

2.1.3 去噪效果评价标准

在图像去噪领域，常用2个评价指标，即峰值信噪比（peak signal-to-noise ratio，PSNR）和结构相似性（structural similarity,SSIM）［15］。PSNR是峰值信号能量与噪声信号平均能量的比值，以对数可变分量（dB）为单位，基于均方误差（mean-square error,MSE）进行评估，定义为

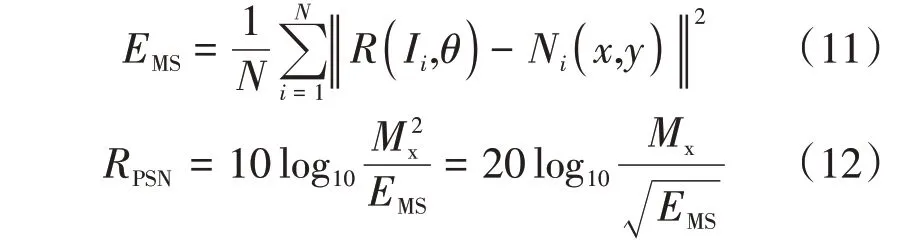
式中：EMS为MSE；RPSN为PSNR；Mx为图像点颜色的最大数值，灰度图借助整数0～255表示，取255。SSIM主要是通过对比原始图像和去噪图像中的结构信息变化，判断图像是否产生失真现象。模型为

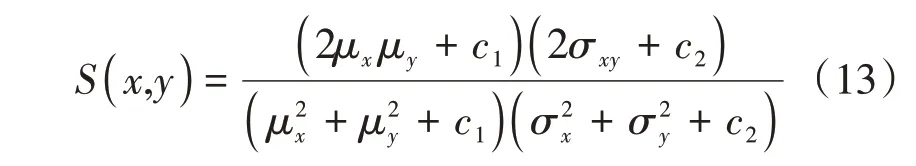
式中：x为去噪图像；y为原始图像；μx为x的均值；μy为y的均值；σx为x的标准差；σy为y的标准差；σxy为x,y的协方差；c1，c2为稳定性常数。

2.2 测试结果

模型训练了100个周期，如图5～9所示。图6～7中图例含义为噪声等级-神经网络卷积层数，图8～9中图例含义为训练集-测试集-噪声等级-卷积层数，其中D为密集条纹，S为稀疏条纹。

图5 σ为50时去噪图像处理

从图6中可以看出，密集条纹网络模型参数检测密集条纹时，神经网络卷积层数增加，去噪效果有一定提升；稀疏条纹网络模型参数检测稀疏条纹时，由图7a～b和图7d～e可知，σ为15、25时神经网络卷积层数多，去噪效果好，由图7c和图7f可知，σ为50时，神经网络卷积层数低，去噪效果好。σ为15时，曲线重合率大，所以条纹密度分类去噪实验中添加噪声的标准差为25和50。此时稀疏条纹网络模型参数检测稀疏条纹，去噪效果较好的卷积层数分别为17和7，因此用密集条纹网络模型参数检测稀疏条纹测试集时卷积层数分别设为17和7；密集条纹网络模型参数检测密集条纹中，卷积层数为17时去噪效果好，因此用稀疏条纹网络模型参数检测密集条纹测试集时卷积层数均设为17。由图8a和图8c可知，σ为25时，密集条纹网络模型参数和稀疏条纹网络模型参数检测稀疏条纹测试集的图像质量相似，在周期为80～100时，密集条纹网络模型参数的去噪效果略微小于稀疏条纹网络模型参数；由图8b和图8d可知，σ为50时,密集条纹网络模型参数检测稀疏条纹测试集的去噪效果远小于稀疏条纹网络模型参数。由图9可知，σ为25和50时，稀疏条纹网络模型参数检测密集条纹测试集的去噪效果明显低于密集条纹网络模型参数。

图6 密集条纹网络模型参数检测密集条纹测试集的PSNR和SSIM平均值

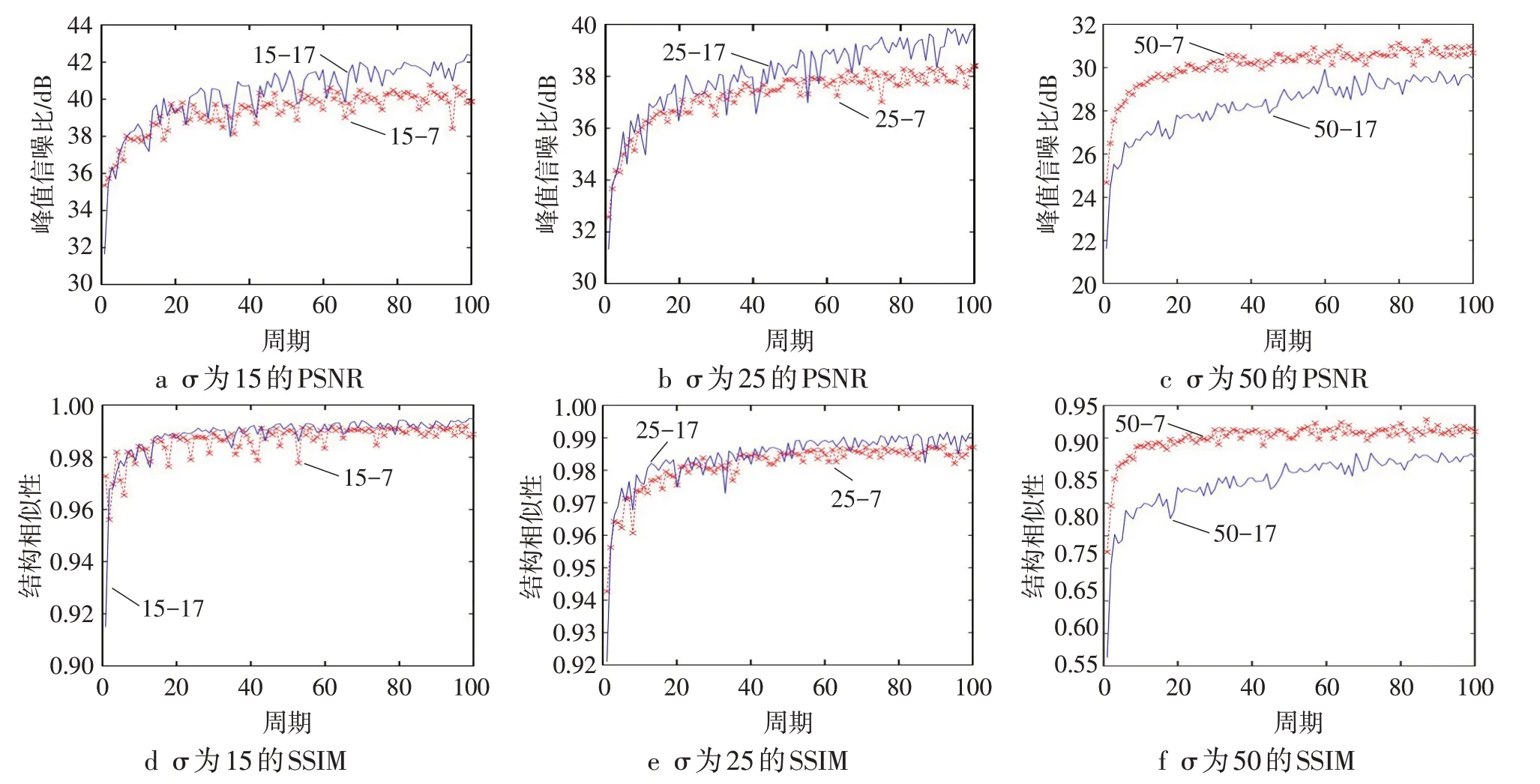
图7 稀疏条纹网络模型参数检测稀疏条纹测试集的PSNR和SSIM平均值

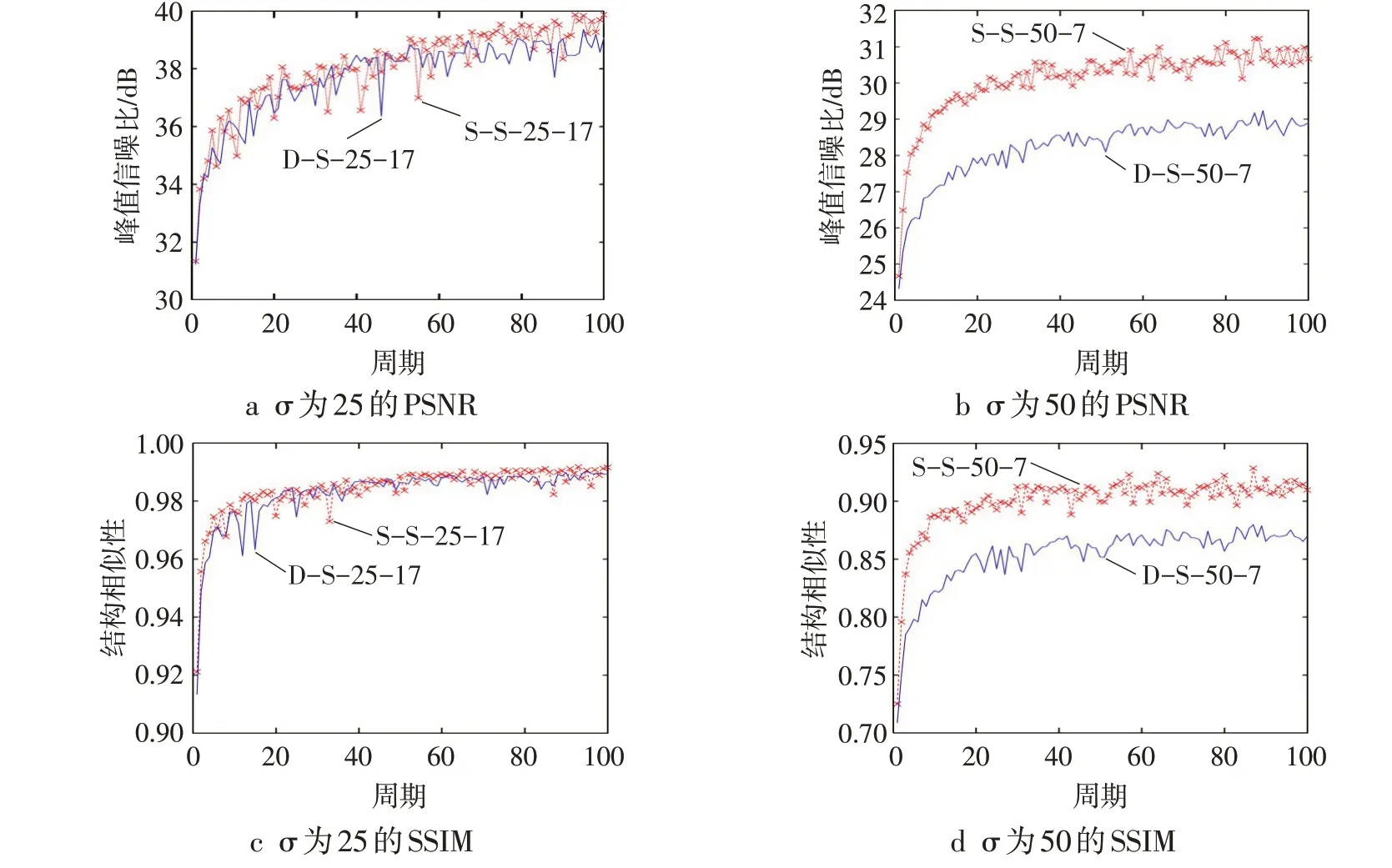
图8 密集条纹网络模型参数检测稀疏条纹测试集的平均PSNR和SSIM

图9 稀疏条纹网络模型参数检测密集条纹测试集的平均PSNR和SSIM

稀疏条纹网络模型参数和密集条纹网络模型参数分别对50张稀疏条纹测试集和50张密集条纹测试集的检测时间如表1所示。σ为25时，条纹密度不分类的DnCNN去噪效果与疏密条纹分类去噪效果对比如表2所示，DnCNN的训练图像是分别从密集条纹图和稀疏条纹图中选取5000张，训练完成后分别对密集条纹测试集和稀疏条纹测试集进行检测。由表1可知，训练集和测试集的条纹密度类型相同时，同样的噪声和卷积层数下，条纹图去噪的处理速度更快。由表2可知，条纹密度分类去噪效果与DnCNN去噪效果没有明显差别，去噪效率明显提升，检测稀疏条纹测试集时处理速度提升了10.62%，检测密集条纹测试集时处理速度提升了11.37%。

表1 不同网络模型参数分别对2个测试集进行检测的时间

表2 σ为25时条纹疏密分类去噪与DnCNN去噪效果

3 结论

文中提出基于深度学习的疏密条纹分类去噪方法，分别训练密集条纹图和稀疏条纹图，生成稀疏和密集2类网络模型参数，输入带噪声的条纹图，调用相应的网络模型参数去噪。调用对应密度的网络模型参数，去噪速度比不对应密度去噪提升约3%，比不分类去噪提升约10%。调用不对应密度的网络模型参数，去噪速度比不分类去噪提升约7%，去噪效果仍可接受。文中提出的算法在基于条纹的实时测量处理实时动态图像以及批量图像去噪时具有速度优势。