基于垂直管道内重油-水两相流动型态的持水率和压降预测模型
2022-01-11黄立华王宜冉程修福文梦鑫康兴照吕仁浩张海鹏何吉祥杨矞琦
黄立华, 王宜冉, 程修福, 文梦鑫, 康兴照, 吕仁浩, 张海鹏*, 何吉祥, 杨矞琦
(1.中国石油大学(北京)重质油国家重点实验室克拉玛依分室, 克拉玛依 834000;2.中国石油新疆油田分公司勘探开发研究院, 克拉玛依 834000)
重油-水流动广泛存在于石油工业中,了解重油-水两相流对石油开采中压力传感器、管道、泵等设备的设计和选型至关重要。目前在水平管中高黏(100~2 000 cP, 1 cP=10-3Pa·s)油水两相流的流动特性已经被广泛研究,但对高密度高黏重油垂直管道油水两相流的研究很少[1-3]。Abubaker等[4]研究表明影响油水两相流动型态以及持水率的因素较多,主要包括:①流体性质,如密度、黏度、界面张力等;②管道特性,如几何形状、尺寸和方向;③操作条件,如温度、压力、流向、流速和流速比。Bai等[5]研究了密度比、界面张力、黏度比等参数对水包油分散流(dispersed flow oil in water, DF o/w)和油包水分散流(dispersed flow water in oil, DF w/o)中油水流动相变的影响。Vuong等[6]在垂直管道中采用高黏油(220~1 070 cP)实验观察到了新的水包油分散流(DF o/w)和油膜中心环状流(annular flow, AF),他们发现由于管壁的润湿效应和油的高黏效应产生的油膜很容易粘附在管壁上,油的黏度对流型和持水率的影响并不显著。随着油水黏度比、密度比和入口含水率的降低,油水滑移效应趋于减弱。在混合流速较低时,滑移效应显著。目前油水两相流研究多采用白油、煤油和轻质原油等低黏油作为介质[7-9],导致大部分现有油水两相流流型的分类和压降分布可能不适用于高黏重油-水系统。
油水两相流压降与其流动型态密切相关,Vuong等[6]研究表明压力梯度与流速、流型和油黏度密切相关,且随着入口含水率和油黏度的增加而增加。Xu等[10]研究了注气量对轻质油水垂直流中的相转化和压力梯度的影响,实验结果表明,注气量不会显著改变发生相转化的临界持水率,但注气后重力压力梯度的变化对压降的影响较大。杨矞琦等[11]对垂直管内油水两相流的流型、持水率和压力梯度等特性开展了相关研究,基于爱因斯坦稀释悬浮液黏度公式,综合考虑压力增黏、稠油剪切变稀以及油水分散状态,建立了高温高压条件下稠油水两相垂直管流压降计算模型,但该模型并未考虑流动型态的影响,尤其对于在油水环状流情况下适用性尚不明晰。总体来说,目前密度大于水的重油-水两相垂直管流流动型态研究均为定性分析,缺乏对不同流动型态下持水率和压降等关键参数的定量研究,尤其是双连续相的重油-水中心环状流压降模型尚未见报道,对进一步深入明晰和预测重油-水流动特性造成一定局限性。
针对上述缺陷,对重油-水在20 mm内径不锈钢垂直管内的流动特性,包括流型、持水率和压力梯度进行研究,基于漂移流模型和动量守恒方程推导得到五种流态下重油-水两相流的持水率预测模型,并基于Bannwart模型建立重油-水中心环状流压降预测模型,以期克服现有轻油-水两相模型对重油-水两相流动持水率和压降预测误差大的难题,为重油举升技术优化提供理论基础。
1 材料及仪器
1.1 材料
油相为透明环烷油(30 ℃时运动黏度为581 mPa·s,密度为1.889 g/cm3),一种主要由环烷烃组成的石油组分,包括环戊烷、环己烷及其同系物,以及4.894%(质量分数)的氯,济南丹龙化工有限公司;水相为自来水;亚甲基蓝,北京博恩试剂有限公司。
1.2 仪器
实验室自主研发的透明可视垂直管流装置[11]。
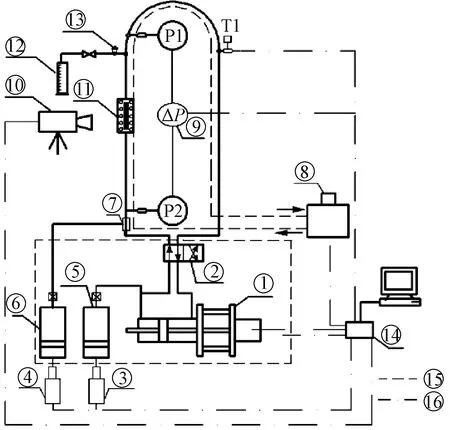
①为循环泵;②为换向阀;③为注入泵A;④为注入泵B;⑤为容器甲;⑥为容器乙;⑦为注入点;⑧ 为Thermo Fisher恒温循环油溶;⑨为差压传感器;⑩ 为高速相机;为可视釜;为油气水分离罐;为背压阀;为数据采集单元;为加热线;为数据采集线图1 实验装置示意图Fig.1 A schematic diagram of the experimental setup
2 主要实验装置和实验过程
2.1 实验装置
实验在自制的装置上进行,以透明环烷油为油相,自来水为水相。实验装置由环形管网系统、流体输送系统、透明可视化观测系统和数据采集系统4部分组成,装置如图1所示。不锈钢倒U形管内径为0.02 m,总长度为5 m,垂直向上、向下管道高度均为2 m。可视釜位于向上的测试段,观测系统包括一个CCD (charge-coupled device)摄像机和一个数据采集单元。可视腔内径为0.02 m,与流管直径一致。使用M7528-MP型相机捕获流动型态,最大显示速率为30帧/s。利用往复式循环泵完成封闭管道内油水混合物的循环流动,并控制油的入口流量,流量调节范围为0.001~0.200 m/s,精度为±0.3%。注入泵B控制水的入口流量,精确度为±0.3%。差压传感器(Validyne, USA)测量P1和P2两个取压点之间的压降ΔP,其间距为2 m,精确度为0.025%。
2.2 实验条件及步骤
注入泵A将油注入往复式循环泵,循环泵将油以定量方式注入垂直管道。水经注入泵B从注入口引入油中,注入口直径为0.006 m。当循环泵中的活塞从一侧移动到另一侧时(10~20 min),一组实验过程结束。入口含水率Iw计算公式为
(1)
式(1)中:Qw和Qo分别是水和环烷基油的流速。表1列出油和水的流速以及实验条件。
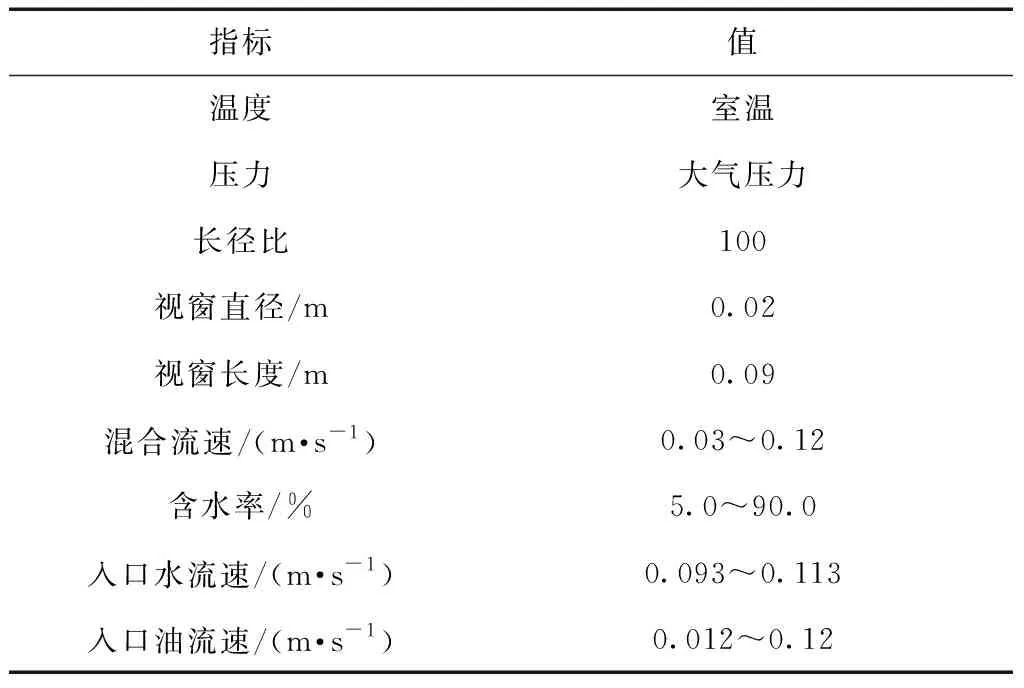
表1 实验条件Table 1 Experimental conditions
在不同的入口含水率下,当流动达到稳定状态后,持续观察并记录流动型态和压降10 min。当一组测量完成时,背压阀打开,流体以恒定的混合流速导入油水分离罐,通过测量油水体积,得到持水率。
3 实验结果与讨论
3.1 重油-水流动型态
在常温、常压下油和水以0.003~0.120 m/s的速度进行混合,实验确定了垂直管道内重油-水两相流的5种流型,分别为油包水分散流(dispersed flow water in oil, DF w/o)、油包水泡状流(bubble flow water in oil, BF w/o)、油包水弹状流(slug flow water in oil, S w/o)、油包水扰动流(churn flow water in oil, CF w/o)、中心环状流(AF)。实验流型图像如图2所示,流型是通过定性和定量两种方式确定的,定量方式确定流型的平均液滴粒径和管道内径的比值δ如表2所示。

图2 在室温和大气压下观察到的高黏度重油-水两相流型Fig.2 High-viscosity heavy oil-water two-phase flow patterns observed under room temperature and atmospheric pressure

表2 δ确定流型的参考范围Table 2 The reference range of δ for determining flow patterns
如图2所示,环烷油为淡黄色,被亚甲基蓝染色的水为深蓝色。当入口含水率较低时,小粒径的水滴分散在油中,随混合流速的增加,流型呈现油包水分散流(DF w/o),如图2(a)所示。随入口含水率的增加,水滴开始聚集,出现了图2(b)所示的油包水泡状流,水滴尺寸小于管道内径。由于湍流能量低,当混合流速为0.003 m/s入口含水率为15%~40%到混合流速为0.120 m/s时入口含水率为20%~33%,易出现油包水泡状流(BF w/o)。随着入口含水率的进一步增加,流型变为油包水弹状流(SF w/o),其中大尺寸的气泡在管道中心被拉长为椭圆形或球形水段塞,如图2(c)。当混合流速为0.003 m/s时入口含水率为40%~65%至混合流速为0.120 m/s时入口含水率为33%~43%,泡状流转化为油包水弹状流(SF w/o)。在较高的入口含水率和较高的流速条件下,由气泡组成的细长尾流出现在水段塞的末端,并形成被水环包裹的中心油流,带有小油滴或气泡夹带的大水段塞不稳定地上升,这种流动被定义为扰动流(CF w/o),如图2(d)所示。混合流速为0.003 m/s时入口含水率为68%~73%到混合流速为0.120 m/s时入口含水率为43%~85%,扰动流极易出现。当入口含水率增加到73%及以上时,出现中心环状流(AF),如图2(e)所示。


表3 不同入口持水率Iw和混合流速Um下水相平均水滴粒径Table 3 Average droplets size of water phase at different input water fractions Iw and mixture velocity Um
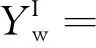
(2)
(3)
式中:θ为接触角,在本实验中θ=20°;μw和μo分别为水和油的黏度;Um是混合流速;Yw为持水率;ρw和ρo分别为水和油的密度;δw和δo分别为水滴和油滴的Sauter平均粒径;s是单位体积的固体表面积;B是一个可调常数,一般对高黏度油取B=0.5。常数kd取值范围为1.5~5[13],油水混合流速最大值Um=0.12 m/s,通过式(1)计算发生相转换时的持水率,结果如表4所示。从表4中可以看出,相转化发生所需的持水率总是高于实验入口持水率,所以在当前实验参数内不会发生相转换。

表4 不同入口持水率下计算的临界持水率Table 4 The calculated critical water holdups at different input water fractions
3.2 持水率测量
在混合流速为0.012~0.12 m/s时,测量不同流动型态下的持水率Yw,并将其与入口含水率Iw对比后,如图3所示。
从图3中可以看出,在低混合流速下,如0.012 m/s和0.048 m/s,即时持水率比入口含水率低,尤其在高入口含水率时油包水段塞流、扰动流和环状流这几种流型发生的情况下,这种现象更加明显。当混合流速大于0.084 m/s时,即时持水率接近对应的入口含水率。这主要是因为在低混合流速下,油水之间由于密度的差异,相滑移更容易发生,密度大的油相上升速度低于密度更小的水相,油相倾向于滞留在管道中,使即时的界面持水率低于入口含水率;当混合流速增加,水相和油相之间的速度差异减小,与入口流速接近,这时,持水率与入口含水率相近。
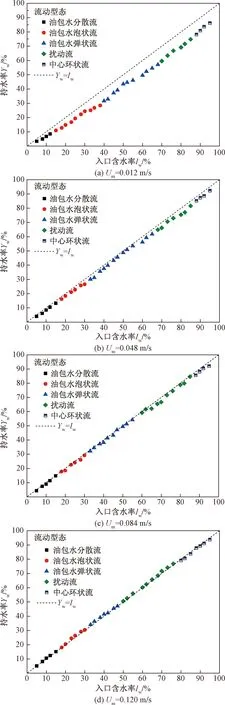
图3 实验测量得到持水率Yw与入口含水率Iw在不同流动型态下的对比Fig.3 Experimental relationships between water holdup Ywand input water fraction Iw under different flow patterns
4 持水率预测模型
持水率的精确预测对油水两相流动的流型和压降预测起至关重要的作用,Zuber等[14]提出漂移流模型研究滑移效应,用于预测油水两相流中的持水率。漂移流模型的表达式为
(4)
Ue=U∞(1-Yw)N
(5)
式中:Usw为水相表观速度;Cw和N分别为相分布参数和粒径指数;U∞为油连续介质中水滴的极限上升速度。基于Harmathy方程[15],结合流体黏度的校正多项式,计算在油连续介质中水滴的极限上升速度,计算公式为

(6)
式(6)中:g为重力加速度;σ为油水界面张力;M为
表征流体黏度的无量纲特性参数,M=[1.81(ρo-ρw)ρw/(μ2g)]。由此可计算得到重油水两相流动中U∞的值为0.115 2 m/s。基于前人有关持水率的研究结果,一些经验方程和数值模型已经被推导,并用来预测轻油水两相流动的持水率,如式(7)~式(11)所示。
Nicolas等[16]模型为
(7)
Hasan等[17]模型为
Co=1.2,N=2
(8)
Flores等[18]模型为
(9)
Bai等[5]模型为
(10)
Bannwart[19]模型为
(11)
在漂移流模型的基础上,推导预测重油水两相油包水泡状流、油包水弹状流、扰动流的持水率预测模型,同时,基于动量守恒方程建立环状流下持水率预测模型。
考虑到研究对象是重油水流动,将式(4)与式(5)合并,并除以(1-Yw)N,可获得Usw/[Yw(1-Yw)N]和Um/(1-Yw)N的线性方程,其中,Cw和U∞分别为斜率和截距。由图4可以看出,对Usw/[Yw(1-Yw)N]和Um/(1-Yw)N的线性方程进行线性拟合后,可得到N的值为3.5,Cw和U∞的值分别等于1.525和0.081 6 m/s。拟合后单个水滴在油连续相中的极限上升速度低于计算值0.115 2 m/s,这可能是由于油相黏度较高,从而影响了水相上升速度。本文中仅定性分析了连续相黏度对分散相液滴极限上升速度的影响,相关量化理论模型还需进一步深入研究。采用同样的方法,对于油包水弹状流和扰动流,同样可以得到当N的值分别为3.1和1.3时,Usw/[Yw(1-Yw)N]和Um/(1-Yw)N之间显示出较好的线性关系,且通过线性拟合的方法,获得油包水弹状流型下,Cw和U∞分别为1.612和0.096 2 m/s;油包水扰动流下,Cw和U∞分别为1.203和0.104 7 m/s。从拟合结果可以看出,分散的液滴极限上升速度随粒径尺寸的增加而增加。

图4 在不同流动型态下Usw/[Yw(1-Yw)N]和Um/(1-Yw)N的线性关系Fig.4 Scatter plot regarding Usw/[Yw(1-Yw)N] and Um/(1-Yw)N under typical flow patterns
从图4中得到的拟合结果与Nicolas等[16]和Han[20]的研究结果类似,粒径指数N的值随分散相液滴粒径增大而减小。考虑到N的值由不同的流动型态决定,如分散流、泡状流、弹状流和扰动流,可以发现拟合得到的N值也随流动型态从分散流转变至扰动流而逐渐降低。并且,从流型图照片中可以看出,在泡状流和弹状流型下,都存在大的水滴或水段塞分布在管道中心,并伴随一些小水滴分布在管壁附近。管道截面的油滴粒径分布呈现明显的抛物线形状,水滴尺寸越大,粒径分布越不均匀,相分布因数Cw值也越大。对于扰动流,由于该流型下,大的水段塞夹杂一些大的油滴或油泡混合式上升,因此扰动流下水相分布更均匀,Cw值也较小。基于漂移流模型和拟合得到的各参数值,可以得到适用于本项研究中几种典型的重油水两相流动型态漂移流模型,即
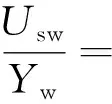
DF w/o & BF w/o
(12)
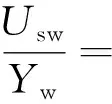
SF w/o
(13)
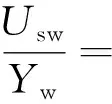
CF w/o
(14)
对于稳定的油为外环的中心环状流,油和水之间的关系可以通过各相的一维动量守恒方程描述。对中心环状流,动量守恒方程为
(15)
式(15)中:dEgo和dEfo分别为由于重力和管壁摩擦阻力造成的单位体积能量损失;dEfw为油水界面处由于油水界面摩擦阻力获得的油相单位体积能量;Uo和Uso分别为油相的入口速度和表观速度;dmo为单位体积油相的质量。dEgo、dEfo和dEfw计算公式为
(16)
(17)
(18)
(19)
式中:Do和Dw分别为油相和水相的水动力学直径;Usw为水相表观速度;l为测试管段长度。λow和λo为基于各相流动状态的摩擦阻力因子,计算公式为
λo=αi(Reo)-ni
(20)
λow=ξαi(Rew)-ni
(21)
式中:参数αi和ni在层流下分别为16和1,紊流下为0.079和0.25;ξ为表征油水界面处由于不稳定动态波影响的校正因子,该值通过实验获得;油相雷诺数Reo和水相雷诺数Rew通过各相水力学直径计算得到,公式为
(22)
(23)
合并式(15)~式(23)可得
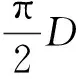
(24)
在式(24)中,除持水率Yw外,校正因子ξ是唯一未知参数,其值可通过实验条件和实验中实际测量的持水率拟合得到,拟合结果如图5所示。
从图5中可以发现ξ的值随水相表观速度Usw增加而降低,并且Usw和ξ之间的关系符合指数定律,可用指数方程描述,即

图5 计算的ξ和Usw之间的关系Fig.5 The relationship between calculated ξ and Usw
ξ(Usw)=a+exp(bUsw)
(25)
式(25)中:参数a和b的拟合值分别为4 628.05和-29.72。将式(25)代入式(24),可最终获得环状流型下持水率预测模型。
通过上文所述漂移流模型和动量守恒方程,将模型预测的持水率数据与实验数据对比后如图6所示。
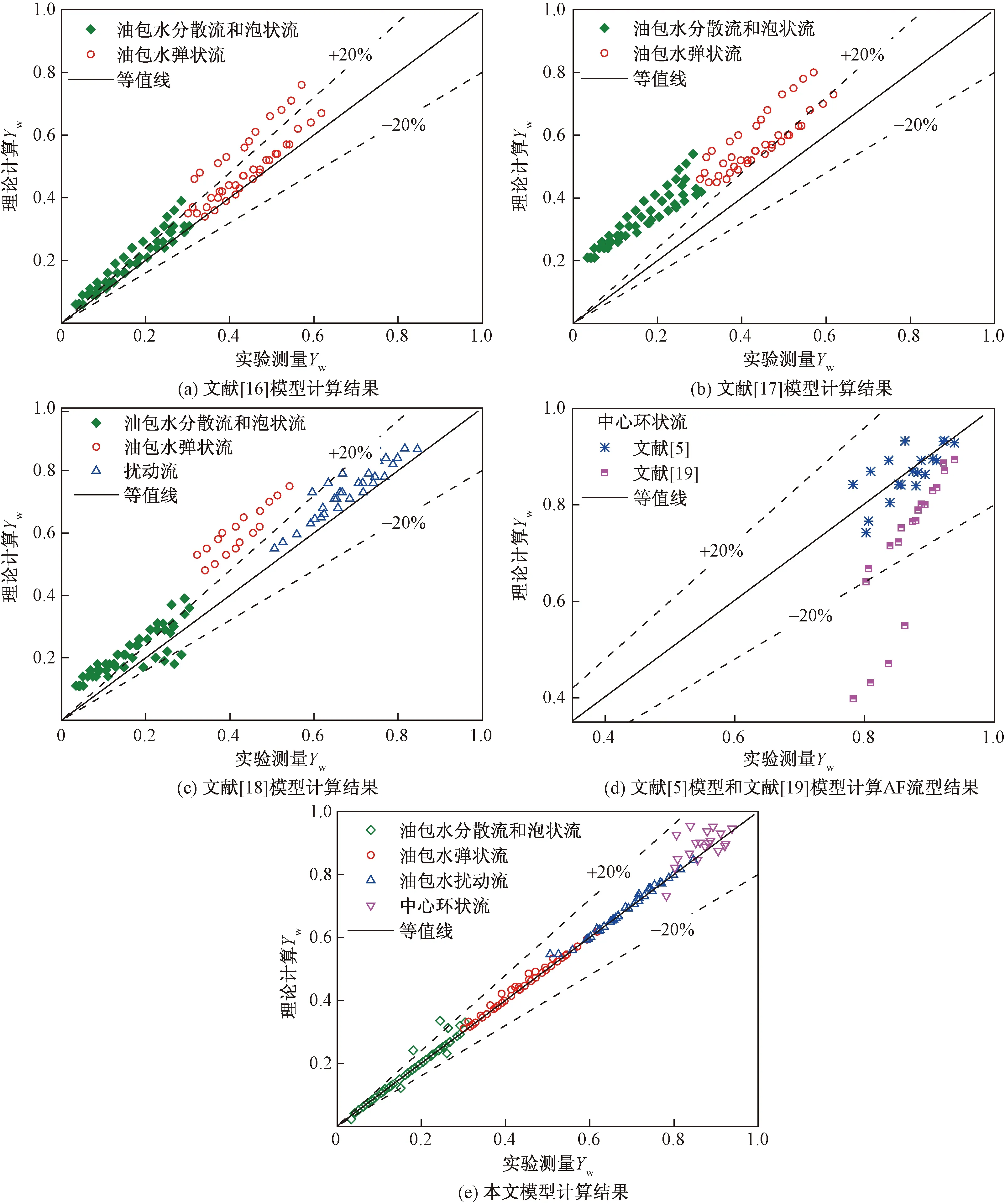
图6 不同模型预测持水率与实验持水率的对比Fig.6 The comparison of predicted and experimental water holdup using different models
从图6中可以看出,通过文献[16]模型预测的在分散流、泡状流和弹状流下的持水率误差率均在20%以内,说明最初应用于低黏轻油水两相流动的文献[16]模型对于重油水流动同样具有一定的精度。而对于图6(b)中所示文献[17]模型预测结果,偏差率高于文献[16]模型。这是由于文献[17]模型中,将水包油泡状流和弹状流下Co和N的值均设置为1.2和2,但实际上分散相分布受流动型态影响较大,该Co和N的值并不适用于重油水两相流动型态。从图6(c)中可以看出,文献[18]模型对扰动流下持水率预测精度较高,说明该模型中的油相分布系数Co和指数N的值能够很好地描述扰动流下分散相的分布状态,但对分散流、泡状流和弹状流型的持水率预测,精度较差。在图6(d)中,文献[5]模型和文献[19]模型对重油水中心环状流的持水率预测精度均较低,相比而言,文献[5]模型比文献[19]模型精度更高,但仍有部分值的误差率大于20%,这可能是因为文献[5]模型和文献[19]模型均是用来预测水为外环、油为中心的轻油水中心环状流持水率,与本文中油为外环、水为中心的重油水中心环状流存在较大差异。采用本文中建立的漂移流修正模型和动量守恒方程,在整个持水率范围内,对分散流、泡状流、弹状流和环状流流型下的持水率进行预测后,均显示了比前人模型更好的预测精度[图6(e)],相对误差率几乎都在20%以内。说明本文建立的基于流型的漂移流修正模型和动量守恒方程在研究重油-水两相持水率预测方面具有一定优越性。通过模型预测持水率对油水两相流动型态判别及其压降的预测具有重要意义。
5 中心环状流压降模型
5.1 理论模型
已有的研究表明,Hagedorn-Brown模型适用于多相流中一相为连续相,另一相为分散相的压降计算,而对于双连续相即中心环状流(AF),Hagedorn-Brown模型并不适用。Bannwart等[19]提出了现象学模型来预测通过垂直管道的油水环状流期间的压降,该模型考虑了环形流体和波状界面中湍流的影响,同时还考虑了浮力对垂直系统的影响。Bannwart的中心环状流模型表示为
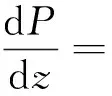
C(ρ2-ρ1)gY(1-Y)
(26)
式(26)中:dP/dz为单位距离压降;ρm为混合密度;D为管道直径;湍流时N=0.25,层流时N=16;ρ2和ρ1分别为外环流体密度和中心流体密度;Y为中心流体积分数。常数b和C是实验中需要调整的参数,在Bannwart的工作中分别设置为0.257和0.159。
因此,对于中心环状流,在Bannwart模型的基础上,将油相和水相作为独立研究对象,分别考虑油相和水相所受作用力,以及外环和中心流体的相互作用力,依据作用力平衡和能量守恒原理,建立了预测油水中心环状流流动压降的现象学模型。
对于中心的水相所受压降损失ΔPfw为
ΔPfw=ΔPgw+ΔPfwo-ΔPbw
(27)
式(27)中:ΔPgw为水相重力损失;ΔPfwo为油水界面摩擦阻力损失;-ΔPbw为水相受油相浮力损失。
对于外环的油相所受压降损失ΔPfo为
ΔPfo=ΔPgo-ΔPfwo+ΔPpo
(28)
式(28)中:ΔPgo为油相重力损失;-ΔPfwo为油水界面摩擦阻力损失;ΔPpo为油相受管壁摩擦阻力损失。
中心环状流时,油水混合物流动压降损失为水相与油相压降损失之和,因此将式(27)与式(28)相加,得到总的压降损失为
ΔP=ΔPgw+ΔPgo+ΔPpo-ΔPbw=
[ρwφw+ρo(1-φo)]g+
(29)
式(29)中:φw和φo分别为持水率和持油率。油相的流动环境可近似为单相环形管流动,在环形管流动中,单相油流的摩擦阻力因子可以描述为
(30)
式(30)中:C和n3为经验系数;Reo为油相雷诺数;μoeff为油相有效表观黏度,可根据均相流中有效黏度压力修正模型求得,即

eε(P-P0)
(31)
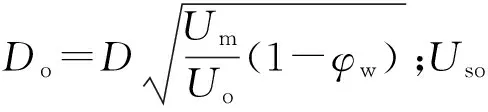
因此建立的油-水中心环状流的压降模型为
ΔP=[ρwφw+ρo(1-φw)]g+
(32)
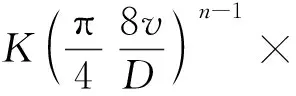
(33)
式中:K为流体的特性黏度;v为流体流速;B2为浮力校正因子。
5.2 模型的验证
为验证不同油水两相流动型态下压降模型拟合度,常温常压条件下,分别将透明环烷油作为重油油相,白油作为轻油油相,自来水作为水相,控制持水率为0~90%,依次出现不同油水两相流动型态,测量不同含水率及流动型态下混合流体在垂直管道中的流动压降,并与文献[21]中的轻油水两相流动压降以及本文建立的分散流模型、中心环状流模型进行拟合分析,结果如图7、图8所示。
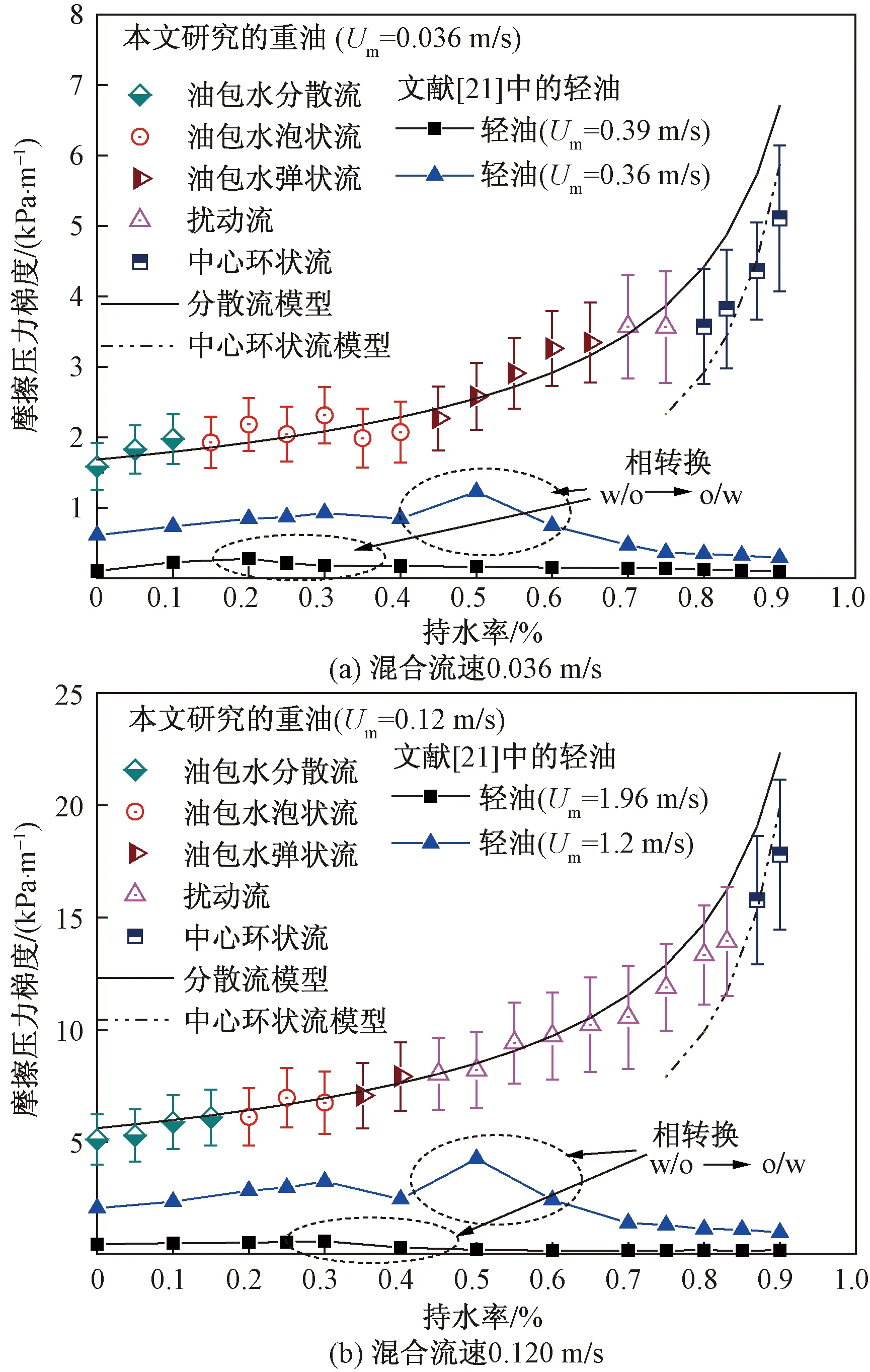
图7 重油水两相与轻油水两相的流动摩阻压降对比Fig.7 Comparison of the current heavy oil water frictional pressure gradients with light oil water two-phase flow
从图7、图8中可以看出,虽然重油水两相的流速远低于轻油水两相,但其摩阻压降和总压降却远高于轻油水两相,这是因为重油的黏度远高于轻油。在重油水两相流动中,摩阻压降随持水率的增加而增加,没有观察到摩阻压降峰值说明相转换并未发生。但轻油水两相流动中,分别在持水率为20%和45%时出现摩阻压降的最大值,即相转换点。在相转换点之后,它们的摩阻压降急剧降低。摩阻压降趋势显示出与相应混合流速下观察到的流动型态密切相关。
相同条件下,重油水两相流动型态与轻油水两相流动型态不同,在重油水流动中,高黏的重油总是与管壁接触的连续相,而低黏的轻油水两相流动在持水率达到一定值后由油包水流动转变为水包油流动,因此流动摩阻降低。对于轻油水两相流,由于水的密度比油大,随持水率增加,摩阻压力梯度与重力压力梯度均增大,因此总压力梯度增加,尽管发生相转换后,摩阻压降大幅降低,但总压降梯度依然显示出重力主导行为。而对于重油水两相流,重力压力梯度随持水率的增加而降低,与摩阻压降梯度趋势相反,因此在摩阻损失较小的情况下,总压力梯度随持水率增加略微降低。而在高混合流速和持水率下,由于摩阻压力梯度比重力压力梯度更重要,总压力梯度与摩阻压力梯度趋势相似。
通过将建立的模型与实验压降数据拟合后得到指数系数n2=0.6,从图7、图8中可以看出,与实验数据对比,分散模型对于油水分散流、泡状流、弹状流、蠕状流和扰动流显示了较好的拟合度;而当C=21.25,B=0.055,n3=0.15时,环状流模型显示了与实验数据较好的拟合度。因此,当设置相应参数值后,通过对比实验与理论计算的压降数据,如图9所示,可以看出,理论计算的压降值均在30%误差范围内,且大部分在20%误差范围内,显示了较高的精确度,说明这两种模型均可用于预测油-水流动压降。
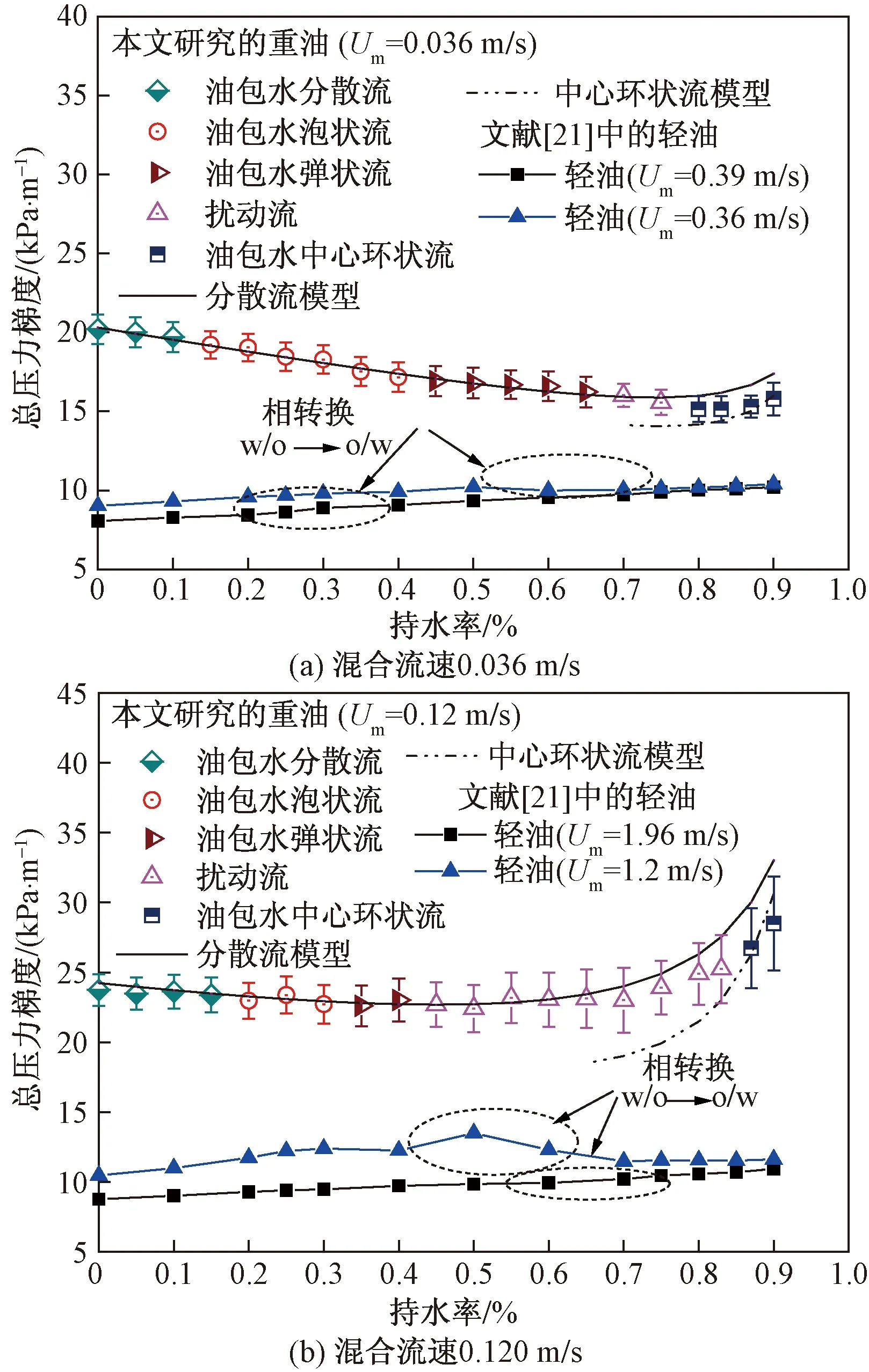
图8 重油水两相与轻油水两相的流动总压降对比Fig.8 Comparison of the current heavy oil water toal pressure gradients with light oil water two-phase flow
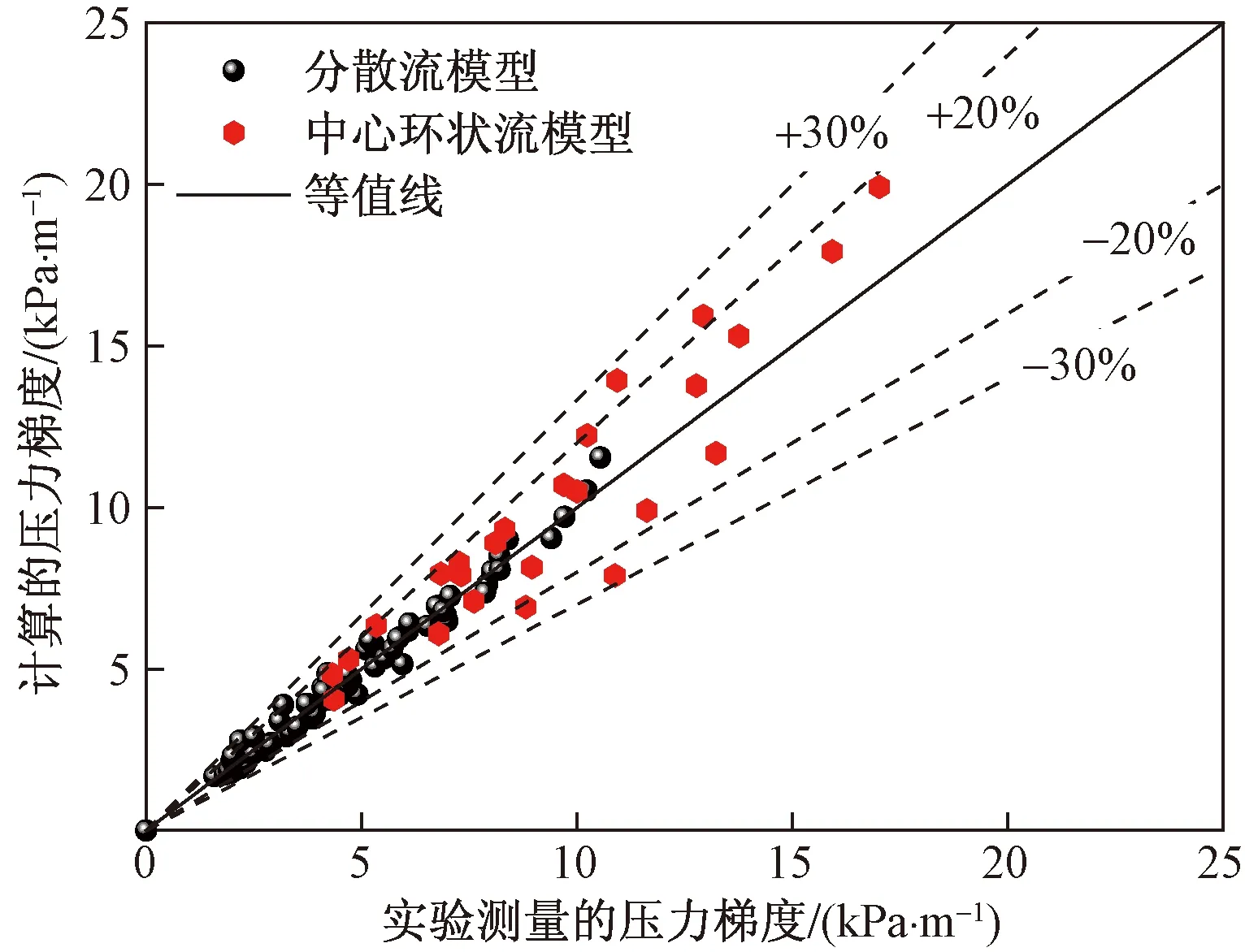
图9 建立的分散模型和中心环状流模型预测压力梯度与实验值对比Fig.9 Comparison between experimental and predicted values of the frictional pressure gradients, obtained by using the dipension model and core-annular model
6 结论
在垂直管内对高黏度重油-水两相流的流动特性进行了实验研究。从获得的结果可以得出以下结论。
油的性质,特别是高密度和黏度,在决定油水流动的流动特性方面起着至关重要的作用。与现有模型相比,本文中提出的基于流型的修正漂移流模型和动量方程对稠油两相流持水率的预测具有更高的精度,误差率小于20%。摩擦压力梯度随着持水率或混合流速的增加而增加,而重力压力梯度随着持水率的增加而显著减小,这导致总压力梯度在低持水率时倾向于以重力为主,而在高混合流速或高持水率时以摩擦阻力为主。基于Bannwart模型建立的中心环状流预测模型预测AF中的压降,偏差均在30%以内,大部分在20%以内,为进一步精确预测重油开采过程中油水两相举升压降和持水率提供了新方法。
