功能梯度形状记忆合金梁的相变力学行为

杨静宁, 唐健, 卢镜宇, 李清禄

(兰州理工大学 理学院, 甘肃 兰州 730050)

功能梯度形状记忆合金(functionally graded shape memory alloy,FG-SMA)是利用SMA和其他材料按照某种含量比率复合而成的新型材料,兼具功能梯度材料和形状记忆合金材料的双重特性[1-2]。FG-SMA材料因其所复合的形状记忆合金在加载过程中会产生相变行为,从而表现出超弹性和形状记忆效应[3]。国内外学者对FG-SMA的制备、实验及其力学特性有了全面的认识,Mahesh等[4]用原位同步辐射X光衍射方法,研究了功能梯度Ni-Ti形状记忆合金丝的循环拉伸变形过程。Khaleghi等[5]对镀钯的 Ti-Ni 板进行扩散退火,从而使富钛 Ti-Ni 形状记忆合金的成分按梯度分布。Bogdanski等[6]研究了Ni-Ti合金的生物相容性以及从纯镍到纯钛的功能梯度样品,有效减少了实验资源。Cole等[7-8]采用直流磁控溅射法在富镍NiTi(Ni56Ti44)基体上沉积富钛NiTi(Ni47Ti53)薄膜,通过控制表征成分的梯度分布，以实现对非弹性变形的恢复产生影响。Viet等[9]基于ZM模型和Timoshenko理论,推导了FG-SMA梁加载和卸载过程中各阶段的弯矩-曲率和剪力-切应变关系的解析模型。Liu等[10]分析了FG-SMA复合材料在热-机载荷的作用下,不同相变阶段相对应的应力分布。薛立军等[11-12]根据固体力学和已有的SMA本构关系,建立了FG-SMA的本构模型,并分析得到了纯弯曲条件下FG-SMA梁、板的力学特性。康泽天等[13]根据形状记忆合金本构方程建立了FG-SMA复合梁的力学模型,研究了FG-SMA梁的变形特性。然而,针对FG-SMA材料的力学性能研究,大都忽略了SMA材料带来的拉压不对称性对结果的影响。

本文结合形状记忆合金的应力应变关系以及临界应力与温度的关系,采用分阶段分步骤的方法分析了梁的相变过程。得到了FG-SMA超静定梁在变形过程中的力学特性与载荷、拉压不对称系数、SMA体积分数以及温度的关系,结果可为FG-SMA材料的设计和优化提供一定的依据。

1 FG-SMA梁的非线性变形

1.1 几何模型

设FG-SMA超静定梁长l,高度h,宽度b。该梁由弹性材料H与SMA材料复合而成,SMA材料的体积分数沿截面高度方向服从f(y)=(y/h)n的函数分布,几何模型如图1所示。其中,n表示体积分数幂指数,y0表示中性轴的初始位置。

图1 FG-SMA梁几何模型

1.2 简化本构模型

基于简化后形状记忆合金材料的本构模型[14],可得到FG-SMA在不同加载条件下SMA的应力值,如图2所示。

图2 SMA简化本构模型

其中,σts,σtf表示受拉侧相变开始和结束时临界应力,σcs,σcf表示受压侧相变开始和结束时的临界应力,εts,εtf表示受拉侧相变开始和结束时的临界应变,εcs,εcf表示受压侧相变开始和结束时的临界应变,εL为最大残余应变。

根据连续介质力学,梁在变形过程中始终满足平截面假定,故梁的轴向应变分布

(1)

式中：yi表示中性轴位置；ρ表示曲率半径。

SMA材料的应力可表示

σSMA=ESMAε

(2)

弹性材料H的应力可表示

σH=EHε

(3)

式中：ESMA表示SMA材料的弹性模量；EH表示弹性材料H的弹性模量。

截面上的平均应力可表示

σ(y)=[1-f(y)]σH+f(y)σSMA

(4)

1.3 拉压不对称系数

考虑到FG-SMA超静定梁在弯曲变形过程中的非对称性,特引入拉压不对称系数[15]

(5)

1.4 本构关系

1.4.1 初始阶段(εt<εts)

初始阶段时,受拉侧表层应变εt小于相变开始临界应变εts,材料全部为奥氏体相,中性轴位移未发生偏移,截面上应力

(6)

式中,EA表示奥氏体弹性模量。

1.4.2 相变阶段(εt≥εts)

随着应变在梁截面上逐渐增大并达到一定值时,FG-SMA梁发生相变且中性轴产生偏移,当梁横截面弯矩为正时,截面及其微段的变形如图3所示。

图3 Ⅰ～Ⅳ阶截面相变及其微段变形示意图

其中A表示奥氏体相,M表示马氏体相,AM表示混合相。当受压侧表层应变εc未达到开始临界应变εcs,受拉侧表层应变εt超过相变开始临界应变εts,即|εc|≤εcs,εts≤εt≤εtf,此时受压侧尚未发生相变,受拉侧出现混合相,混合相与奥氏体相形成相边界BTA,进入Ⅰ阶相变,如图3a)所示,截面上应力

(7)

当εcs≤|εc|≤εcf,εts≤εt≤εtf,受压侧表层开始发生相变并出现混合相,受压侧混合相与奥氏体相形成相边界BCA,进入Ⅱ阶相变,如图3b)所示,截面上应力

(8)

当εcs≤|εc|≤εcf,εtf≤εt,受拉侧表层应变εt超过受拉侧相变结束临界应变εtf,受拉侧表层出现马氏体相,而受压侧表层仍处于混合相,受拉侧混合相与马氏体相形成相边界BTM,如图3c)所示,进入Ⅲ阶相变,截面上应力为

(9)

当εcf≤|εc|,εtf≤εt,受压侧表层应变εc超过受压侧相变结束临界应变εcf,受压侧表层出现马氏体相,受压侧混合相和马氏体相形成相边界BCM,进入Ⅳ阶相变,如图3d)所示,截面上应力为

(10)

式中:yi(i=Ⅰ,Ⅱ,Ⅲ,Ⅳ)表示不同阶段截面上中性轴位置;Δh=yi-y0表示中性轴位移,相边界A1A,B1B,C1C,D1D的坐标分别为yA1A=yi-εtsρ,yB1B=

当梁横截面弯矩为负时,截面及其微段的变形相变过程与弯矩为正时的情况类似,不再赘述。

1.5 临界应变模型

由形状记忆合金临界应力与温度的关系[16],马氏体相变起始应力和结束应力与温度的表达为

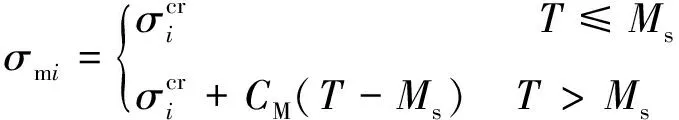
(11)

式中：下标i取s与f时分别表示相变起始和结束时的临界应力；Ms表示马氏体相变起始温度；CM为常数。

将马氏体相变起始应力值σms和相变结束应力值σmf分别作为相变起始应力σts,σcs和相变结束应力σtf,σcf代入(7)～(10)式中,即可得到温度、荷载、幂指数、拉压不对称系数与曲率、中性轴位移、相边界之间的关系。

1.6 平衡方程

初始阶段,梁的平衡方程为

Ⅰ阶相变阶段,梁的平衡方程为

Ⅱ阶相变阶段,梁的平衡方程为

Ⅲ阶相变阶段,梁的平衡方程为

Ⅳ阶相变阶段,梁的平衡方程为

式中

M(x)=

2 结果与讨论

设FG-SMA超静定梁长、宽、高为l=200 mm,h=20 mm,b=15 mm,受均布载荷q以及集中载荷F作用,模型如图1所示。选用Ni55Ti材料,相关参数为[16]

2.1 中性轴位移

图4a)～4d)分别表示载荷、拉压不对称系数、幂指数以及温度对截面中性轴位移的影响。计算结果显示:不论弯矩为正还是为负,中性轴都率先向截面受压侧移动,且中性轴位移随载荷的增大而增大;中性轴位移随着拉压不对称系数的增大而减小,但影响较小;幂指数越大,中性轴位移越小;随着温度的升高,中性轴位移减小,且温度越高,影响越小。

2.2 曲率

图5a)～5d)分别表示载荷、拉压不对称系数、幂指数以及温度对曲率的影响。计算结果显示:进入相变阶段以后,在最大正负弯矩处,即x=100 mm和x=200 mm处,曲率分别达到最大值。曲率随着载荷的增大而增大;曲率随着拉压不对称系数的增大而减小,但影响较小;曲率随着幂指数的增大而减小;曲率随着温度的升高而减小。

图4 中性轴位移与截面位置的关系

图5 曲率与截面位置的关系

2.3 相边界

图6a)～6d)分别表示载荷、拉压不对称系数、幂指数以及温度对相边界的影响。计算结果显示:相边界随着载荷增大越远离截面边缘;拉压不对称系数对受拉侧相边界影响不大,但可以看出对受压侧相边界影响较大,且随着拉压不对称系数的增大而越靠近截面边缘;相边界随着幂指数的增大越靠近截面边缘,且幂指数越小,越易发生相变;相边界随着温度的升高越靠近截面边缘,且温度越高,影响越小,越不易发生相变。

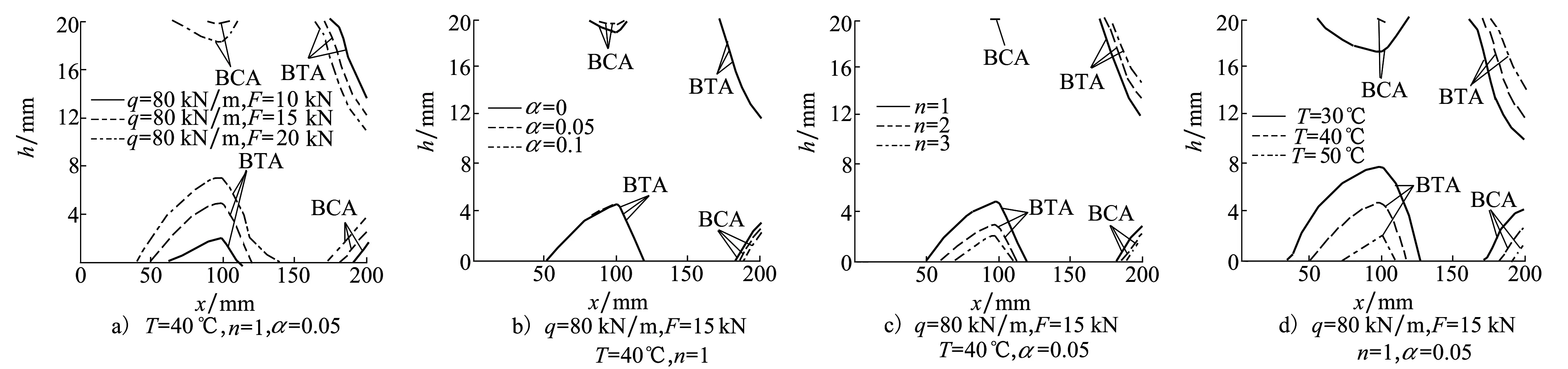
图6 相边界与截面位置的关系

3 结 论

1) 在相变阶段,中性轴位移随着载荷的增大而增大;在分别改变幂指数和温度时,中性轴位移随着幂指数的增大和温度的升高而减小,但影响较小。

2) 初始阶段,载荷、幂指数和温度对曲率影响较小,在相变阶段,曲率在x=100 mm和x=200 mm处分别达到最大值,且曲率的变化量随载荷的增大而增大,而随着幂指数的增大和温度的升高而减小。

3) 相边界随着载荷的增大越远离截面边缘,随着幂指数的增大与温度的升高越靠近截面边缘,越不易发生相变。

4) 对功能梯度形状记忆合金梁而言,由于SMA的体积分数沿着截面高度呈幂指数变化,一定程度上降低了拉压不对称性对材料力学性能的影响。