对转压气机变转速比失速特性试验研究

王昊, 薛飞, 岳少原,2, 王掩刚

〗1.西北工业大学 动力与能源学院, 陕西 西安710072;2.中国空气动力研究与发展中心 空天技术研究所, 四川 绵阳621000

旋转失速作为轴流压气机中一种常见的流动失稳现象，是叶轮机械中最严重的气动灾难之一(另一个为喘振)[1]。从表面来看旋转失速与喘振出现时的共同特征都是发动机产生巨大的轰鸣声，然而这两种流动失稳的内在物理机制并不相同[2]，所引发的后果也有很大的差异。由于发生旋转失速时存在迟滞效应，此时唯一的方法是降低转速，但是会造成压升急剧降低，使得旋转失速更难以退出失稳工况。与喘振相比，旋转失速是飞行员更不愿面对的灾难。

据Stenning[3]记载，Whittle首次在试验中发现当流量减少到一定程度时，在压气机中存在旋转失速现象以来，国内外学者对此进行了广泛而持续的研究。随着对压气机失稳机理的不断研究，目前公认的失速先兆类型有2种[4]：大尺度的模态波型失速和小尺度的突尖波型失速。1989年McDougall等[5]采用空间傅里叶分析法对信号进行处理，在1台单级低速轴流压气机中检测到了周向传播速度为50%转子速度的模态型失速先兆。由于模态型失速先兆对压气机的破坏性相对较小且可逆向恢复，研究人员更关注突尖扰动引起的失速扰动。Day[4]在1台轴流压气机中首次发现了突尖型失速先兆，该扰动完全不同于模态扰动，起源于转子叶顶前缘区域且呈现三维、短尺度特征，通常占据一个或几个叶片通道。随后Camp和Day[6]通过试验发现突尖型失速先兆发生于转子叶顶区域, 其周向传播速度为70%～80%转子转速且发展十分迅速，仅仅经过几转就直接发展为旋转失速。在发展过程中伴随着扰动尺度逐渐增大且周向传播速度逐渐衰减，当发展为成熟的失速团时，传播速度降低为20%～50%转子转速。但是压气机在失速时，往往不仅仅出现一种失速先兆，Houghton[7]发现即使模态型扰动波已经出现，也有可能再出现突尖扰动，随后由突尖扰动直接引起失速。经过长期的研究，目前学术界对于常规转子-静子交替布局压气机中的失速现象已经有了一定的认识。

对转压气机作为一种具有尺寸小，重量轻优势的新型压气机结构，得到了研究人员的关注。由于前后转子相互独立工作的特点，转速比对其内部流动具有很大的影响，导致其内部的失速过程相较常规压气机更加复杂。高丽敏等[8-10]采用数值方法研究了对转压气机中的失速过程，结果显示当转速比在0.7～1.11之间时，前后转子之间的转速差对失速初始扰动类型无本质影响；在不同转速比下压气机的失速边界存在差异，且二次泄漏流在轴流对转压气机的非稳定流场失稳过程中起着至关重要的作用。Mao等[11]数值研究了周向槽机匣处理对对转压气机稳定裕度的影响，结果表明了周向槽可以抑制失速。王掩刚等[12]应用数值分析手段研究了叶顶间隙对对转压气机性能参数的影响规律。徐强仁等[13]应用三维非定常数值手段研究了高负荷对转压气机尾迹涡对叶顶泄漏流的影响。岳少原等[14-15]通过试验研究了对转压气机中的流动不稳定现象，捕捉到了一种不同于模态失速先兆和突尖失速先兆的失速类型，与常规动静交替布局的压气机具有明显的区别，其失速扰动的产生及消亡具有突发性，并且失速扰动沿周向的旋转速度远低于转子转速。

从公开的文献来看，研究人员针对新几何构型的对转压气机开展了大量的研究工作，丰富了研究人员对其流动机理和规律的认识。但大部分的研究以数值分析的手段开展，有关流动失稳的研究还有待加强，少量的以试验研究的结果还与数值研究结果所获得结论存在明显差异，这严重制约了研究人员对该类新型结构压气机流动失稳的认识。本文以西北工业大学低速轴流对转压气机试验平台为对象，应用试验手段开展对转压气机流动失稳的探索工作，丰富对转压气机非稳态试验数据，分析不同转速比条件下对转压气机的失速特性，为进一步深入理解对转压气机中的流动失稳现象提供支撑。

1 研究对象及试验方案

1.1 试验台介绍

本文所研究的对转压气机由进口导叶(19)、上/下游对转转子(21/21)组成，上下游对转转子由2台变频电机独立驱动和控制，设计转速2 400 r/min，叶顶间隙0.5 mm，设计点流量6.4 kg/s，压比1.07。顺着气流方向望去，前转子沿顺时针转动，后转子沿逆时针转动。采用PID技术将转子转速相对误差控制在0.1%以内。通过控制节流锥的轴向位置改变流经压气机的空气流量，当发生喘振等紧急情况时，可控制电磁放气阀放气实现压气机快速退出危险工况。

图1为对转压气机总体布局。通过大气温度变送器捕捉到的当地温度Tatm结合当地大气压patm可以获得当地大气密度ρatm，再通过进出口壁面静压孔得到的进口平均静压pi,ave和出口平均静压pe,ave结合布置在前转子前端球头五孔探针获得的压气机进口气流速度轴向分量Vix、压气机进口气流平均总压pti，可以计算得到流量、总静压升、流量系数和总静压升系数，进而获得压气机特性曲线。计算过程如下：

(1)

式中：ε为膨胀系数，对于本文中的对转压气机实验台，由于Mai<0.3，ε取1即可；Ai为压气机进口流通面积，单位为m2。由(1)式可以计算得到压气机进口气流质量流量。

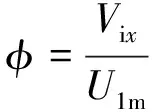
(2)

利用(2)式即可得到进口流量系数。其中U1m为压气机前转子中径线速度，利用前转子叶片叶顶及叶根直径和转速计算得到。

Δp=pe,ave-pti

(3)

(4)

利用(3)式和(4)式便可得到总静压升Δp和总静压升系数Ψts。

图2为动态压力传感器布局方案，总共采用了31个高频动态压力传感器，其中1～9号传感器布置在前转子叶顶弦长方向，10～17号传感器布置在后转子叶顶弦长方向，1号及18～24号传感器沿周向均布在前转子前缘平面，11号及25～31号传感器沿周向均布在后转子前缘平面。2个光纤传感器(L1,L2)分别布置在前后转子弦向中间位置以实现前后转子的锁相功能。在前后转子某叶片叶顶分别涂上反光材料，其余叶片叶顶涂黑。当此叶片经过光纤传感器时会被捕捉到，进而触发高频动态压力传感器采集信号，以实现前后转子的锁相功能。在本文试验中，动态压力传感器的采样频率为5.120 kHz，传感器响应频率为20 kHz。

图1 对转压气机试验台的总体布局

图2 动态压力传感器总体布局

1.2 转速配置以及特性录取方案

为研究不同转速比以及相同转速比不同转速对对转压气机失速类型的影响，目前研究人员主要针对前后转子转速比为0.7～1.4区间进行分析[8-9]。本文共设计了3组试验方案，分别为转速比小于1(包含0.75,0.857,0.875,0.889)，等于1及大于1(包含1.125,1.167,1.333)。相同转速比下分为不同的转速配置，共包含19种转速配置，涵盖了低-中-高的转速范围, 从而研究同一转速比下，压气机低转速、中转速及高转速的失速过程的变化规律。定义转速比为Rr=n1∶n2，其中n1代表前转子转速，n2代表后转子转速。表1给出了试验测量的3组试验方案详细的转速设计。

采集特性曲线的过程，均采取以下方案，以8号试验(转速比等于1)为例进行说明。设定上、下游转子转速分别为目标转速，随着节流锥从全开状态缓慢关闭，压气机流量系数降低、压升系数升高，压气机特性曲线呈现稳定状态的stable1段。当节流锥关闭到一定程度时，在线叶顶动态压力传感器阵列显示其内部流动首次出现强烈波动，在特性曲线上记录为近失速B点，此时保持节流锥不动，压气机特性曲线经历了压升系数急速下降和流量系数剧烈波动的过程，特性线记录为图3所示的B-C失速发展(stall occur)过程。在工况C继续关闭节流锥到工况D再缓慢打开到工况E，此时压气机内存在完全发展的失速团沿周向转动，流量系数及总静压升系数变化平缓。随后，给节流锥一个打开状态的微小扰动后保持节流锥位置不动，压升系数又经历了急速抬高、流量系数略有增加的过程，最终稳定在特性曲线F点，特性线上记录为E-F失速恢复(recovery stall)过程。继续缓慢打开节流锥，压气机流量系数增加，压升系数减小，叶顶动态压力阵列信号重新恢复稳定。至此节流锥已遍历完所有的目标位置，通过分析进出口壁面静压孔采集到的数据，即可得到该转速配置下的特性曲线。其他转速比条件下，按照此流程均可得到对应的具有迟滞行为的特性曲线，这里不再赘述。下文分析的失速边界均按照此方法试验获得的近失速B点作为压气机特性曲线上最后一个点。

通过处理叶顶机匣壁面动态压力传感器采集的信号，得到8号试验失速起始阶段机匣壁面压力波沿周向的传播过程,如图4所示。从图中可知失速初始扰动首先出现在后转子前缘(25号传感器)并快速向上游及下游扩张，0.1s后前转子前缘也检测到了失速扰动并且快速增长为完全发展的失速团。失速团周向跨度为135°，传播方向与后转子转向一致，失速团转速约等于转子下游转子转速的8%，这说明本文所研究的对转压气机在近失速点捕捉方面有较高的精度，试验结果可以用于分析对转压气机转速比对其失稳边界影响规律。

图3 总静压升系数-流量系数曲线图4 失速起始阶段壁面压力轨迹

2 试验结果与分析

2.1 转速比对压气机失速边界影响

图5为19种转速配置下对转压气机流量(Q)-总静压升(Δp)特性曲线，图例参考表1，例如：前后转子转速分别为900 r/min和1 200 r/min对应第一组试验的1号，则将其命名为1.1，按照此命名规则对所有转速配置进行命名。图中红色、蓝色、黑色曲线分别代表转速比等于1、小于1及大于1的情况，紫色曲线代表压气机失速边界线。图中失速边界线为所有转速配置下共同失速边界，该失速边界总体呈现出折线特征，与常规压气机中失速边界形态有所区别。以2 100(r·min-1)/1 800(r·min-1)(转速比1.167)和1 800(r·min-1)/2 100(r·min-1)(转速比0.857)的转速配置为例，在前/后转子转速值互换的情况下，从失稳难易程度方面讲，转速比小于1的特性曲线相比于转速比大于1的失速点更靠近左边，即转速比小于1时对转压气机更难失稳。从增压能力方面讲，转速比大于1的特性曲线相比于转速比小于1的更靠上方，即转速比大于1时压气机增压能力更强。这是由于当转速比大于1时，前转子转速更大，对气流的做功能力更强。而在后转子之前去除了静子叶排，使得后转子的流场更加复杂且难以组织。因此后转子不仅有增压的作用，而且还承担着将前转子对气流所加的功转化为压力势能的功能。所以当进口气流流量相同时，转速比大于1时的增压能力更强。通过前后转子进出口的速度三角形亦可以进行分析。

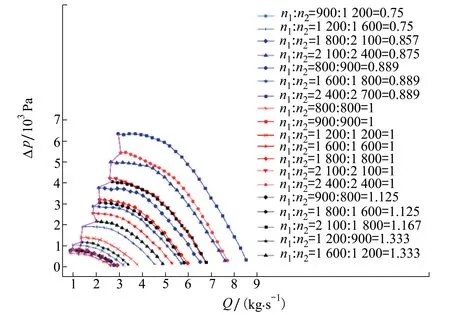
图5 不同转速配置下对转压气机流量-静压升特性曲线及失速边界

图6为当前/后转子转速互换且质量流量一致时速度三角形示意图。此时各转速比下前转子进口气流绝对速度C1in相同。由于前后转子转速不同，如图所示Rr<1和Rr>1的前后转子转速均与Rr=1的转速相差 ，致使前转子出口绝对速度C1out即后转子进口绝对速度C2in和后转子出口绝对速度C2out方向存在一定差异。轮缘功Lu反应了压气机对气流的加功量，即轮缘功越大，增压能力越强，计算公式如(5)式所示

Lu=Cout,uUout-Cin,uUin

(5)

式中：Cout,u和Cin,u分别为转子出口和进口绝对气流周向分量;Uout和Uin分别为转子出口和进口圆周速度。对于对转压气机而言，同一转子进出口Uin和Uout相同，(5)式可简化为

Lu=UCout,u-Cin,u)

(6)

图6 前后转子转速互换时速度三角形示意图

将(6)式结合图6可以发现当气流通过前转子时，转速比大于1对应的出口-进口绝对气流周向分量之差(C1out,u-C1in,u)和转速U比转速比小于1时更大，轮缘功更大。对于后转子而言，转速比小于1时对应的轮缘功更大。将前后转子综合来看，转速比大于1时对应的前后转子总轮缘功更大。反映在图5中即当前后转子转速互换时，转速比大于1时的特性曲线更靠近上方，即相同流量条件下，增压能力更强。通过试验可以发现其他符合条件的转速配置均满足该规律，即前/后转子转速值互换的情况下，转速比越大压气机增压能力越强，同时稳定性更差。

由于前后转子相互独立，转速越大表明压气机做功能力的增强。为方便说明，定义前后转子平均转速Rave=(n1+n2)/2。为更清晰的表达压气机在Rave相等的情况下的增压和失稳规律，分别定义Δmstall和ΔpRstall分别为前/后转子转速值互换时，转速比大于1情况下相比于转速比小于1情况下的失速起始点流量增量和静压升增量。通过对表1中前/后转子转速值互换的试验组进行试验，表2列举了Δmstall及ΔpRstall的详细结果。表中编号与表1一致，Qini为失速起始点流量，Δpini为失速起始点静压升。可以发现：当前/后转子转速值互换时，转速比大于1的压气机相比于转速比小于1的情况更容易失速，且失速起始点流量提前至少18%左右。与此相反，转速比大于1的压气机相比于转速比小于1的情况增压能力更强，且失速起始点增压能力至少高出5.5%。不同的转速比下，压气机增压能力与稳定性相互制约。从上文分析来看，转速比对于对转压气机的特性曲线分布规律具有重要的影响作用，这里以转速比作为分类依据，对对转压气机的失速边界进行进一步的讨论。

表2 前/后转子转速值互换时失速起始点性能参数随转速比的变化

图7为5种转速比下的对转压气机流量-总静压升特性曲线，共包含16种转速配置。图中曲线分别代表转速比为1的7种转速配置、转速比为0.75的2种转速配置、转速比为0.889的3种转速配置、转速比为1.125的2种转速配置、转速比为1.333的2种转速配置，同时采用对应颜色标记出了各转速比下的独立失速边界。可以看到：在各转速比下，失速边界比较光滑，与常规压气机失速边界形式一致。不同的转速比下，失速边界存在差异，相互独立。因此相比于常规压气机，对转压气机的失速边界与转速比有很大关联。为了更加直观地反映转速比对对转压气机特性曲线的影响，图8为5种转速比下的对转压气机流量系数-总静压升系数特性曲线，图中颜色与转速配置的对应关系与图7一致。可以发现：当转速比相同时，不同转速下的无量纲特性曲线具有比较高的重合度，而不同转速比之间的无量纲特性曲线存在明显的差异。除此之外，在相同的流量系数下，静压升系数随着转速比的增大逐渐减小，特性曲线向下方移动。由于当流量系数相同时，不同转速比下的前转子进口速度三角形相似，若转速比也相同，则前后转子进出口的速度三角形均相似。因此相同转速比下，不同转速的无量纲特性曲线几乎重合。

图7 不同转速比下对转压气机流量-静压升特性曲线及失速边界

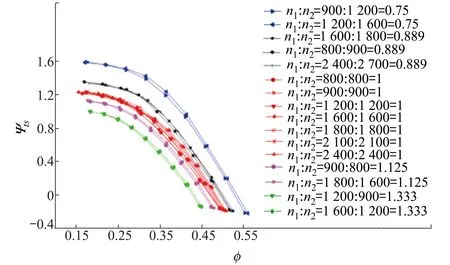
图8 不同转速配置下对转压气机流量系数-总静压升系数曲线

图9为当流量系数相同时，Rr<1，Rr=1和Rr>1时前后转子进口速度三角形分布。由于转速比相同的情况下，只要流量系数相同即进口速度三角形相似，压气机无量纲压比就相同。因此，不失一般性，此处对于无量纲压比的分析，可将Rr>1,Rr=1和Rr<1情况下的进口速度三角形按全等处理。当转速比不相同时，由于前转子进出口速度三角形均相同，结合(6)式可得此时前转子所做轮缘功相同。当气流经过后转子时，Rr>1时出口绝对气流周向分量与转速方向相反为-ΔU，Rr=1时出口绝对气流方向沿轴向，Rr<1时出口绝对气流周向分量与转速方向相同为ΔU。故随着转速比减小，后转子出口和进口绝对气流周向分量之差(C2out,u-C2in,u)和转速U增大，Lu更大。综合前后转子来看，随着转速比减小，对转压气机的增压能力更强，最终形成如图8所示的不同转速比下特性曲线具有差异性的分布规律。

图9 不同转速比下的速度三角形示意图

2.2 变转速比失速初始扰动分析

上文表明转速比对对转压气机的特性曲线及不同转速比下的失速边界有重要的影响。为进一步深入研究对转压气机在不同转速配置下近失速时的内部流动状态，对所有试验组进行试验并分析。表3列举了所有转速配置下对转压气机失速扰动类型及基于后转子转速的失速团旋转速度归纳结果。可以发现：当转速比等于1时，不同转速配置下失速起始阶段前后转子中的失速扰动均占据周向135°范围，周向旋转速度大约为后转子转速的6%～8%，传播方向与后转子旋转方向一致，基于后转子的失速旋转速度随着Rave增大而减小，且在相同的Rave条件下，随着转速比的增大，该值减小。图4展示了前后转子转速均为800 r/min时压气机壁面压力信号，此时失速扰动周向旋转速度大约为后转子转速的8%。在转速比小于1的所有转速配置下，失速扰动特征与转速比等于1时类似，不同的是失速扰动周向旋转速度大约为后转子转速的10%～18%。在转速比大于1的情况下，失速扰动特征比较复杂。当转速比为1.125时，失速扰动特征与转速比小于等于1时相似，失速扰动以后转子旋转方向在周向以3%～4%后转子转速进行周向旋转。综合来看，当转速比小于等于1.125时，失速扰动占据周向135°范围，并以后转子旋转方向在周向以3%～18%后转子转速旋转。

表3 不同转速比条件下对转压气机失速扰动特征及初始扰动频率

这与旋转速度通常大于50%转子速度，周向通常占据2～3个叶片通道的典型突尖波[6]相似但存在差异。为方便描述，将这种周向尺寸远大于突尖波且旋转速度远低于突尖波失速扰动特征记为类突尖波。当转速比为1.167和1.333时，失速扰动特征出现了明显变化。此时失速扰动与突尖波或者模态波扰动都存在明显的区别，扰动固定在机匣周向的某个范围内，不沿周向传播。如图10所示，在转速比为1.333时，前后转子的失速初始扰动均固定在周向大约225°范围内，故不存在初始扰动频率。该现象与常规压气机中的失速特征具有很大的差异。因此，尽管对转压气机在不同转速比下的特性曲线并无太大区别，但其中的失速扰动特征存在很大差异。

图11为不同转速比下失速扰动特征的归纳结果，数据来源表3中19个转速配置下的失速扰动特征。图中采用黑色代表转速比小于或等于1.125的失速扰动特征，红色代表转速比大于或等于1.167的失速扰动特征。当前/后转子转速比小于或等于1.125时，失速扰动沿周向旋转。当转速比大于或等于1.167时，失速扰动不沿周向旋转。对于本文所研究的对转压气机，转速比存在一个临界值，该值位于1.125～1.167之间，当转速比小于该临界值时，失速扰动绕周向旋转，与常规压气机类似。当转速比大于该临界值时，失速扰动不沿周向旋转，该现象与常规压气机具有显著差异。

图10 转速比为1.333时失速起始过程壁面压力轨迹图11 不同转速比下失速初始扰动特征的归纳结果

图12为不同转速比下失速初始扰动频率随Rave的变化规律，共包含16种转速配置。其中红色代表转速比小于1的情况，蓝色代表转速比等于1的情况，黑色代表转速比等于1.125的情况。总体上，转速比越小，失速初始扰动频率越高。在同一转速比下，失速扰动初始频率随Rave的增大而增大，表明失速初始扰动的旋转速度或个数有所增加。

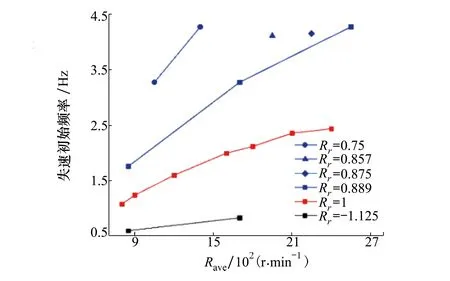
图12 失速频率随平均转速的变化规律

3 结 论

本文以低速轴流对转压气机为试验平台，通过设置转速比小于1、等于1以及大于1共19种转速配置并进行试验，成功捕捉到了所有近失速点及不同转速比条件下的失速边界特征。通过对所有转速配置下的失速扰动特征进行分析可得到如下结论：

1) 在前/后转子转速值互换的情况下，转速比大于1相比于转速比小于1时压气机更容易失速，增压能力更强，且失速起始点流量提前至少18%，增压能力至少高出5.5%。不同的转速比下，压气机增压能力与稳定性相互制约。相比于常规压气机，对转压气机的失速边界更复杂，不同转速比下的失速边界相互独立。

2) 当转速比相同时，相同流量系数下，前后转子进出口速度三角形均相似，压气机压升系数相等，因此等转速比下无量纲特性曲线几乎重合。当转速比不同时，随着转速比减小，相同流量系数下对转压气机后转子所做轮缘功变大，增压能力变强，无量纲特性曲线向上方移动。

3) 对于对转压气机，存在一个临界转速比值位于1.125～1.167之间。当转速比小于该临界值时，失速扰动占据周向大约135°范围，以3%～18%后转子旋转速度沿与后转子相同的旋转方向进行周向旋转，失速扰动特征为类突尖波。此时转速比越小，失速初始扰动频率越高，且在同一转速比下，失速扰动初始频率随Rave的增大而增大。当转速比大于该临界值时，失速扰动固定在周向某一位置，不沿周向旋转，该现象与常规压气机具有显著差异。

通过本文试验研究，认识到对转压气机中失速过程的复杂性，未来应采用更精细的测量设备及更先进的数据分析手段清晰地刻画对转压气机中的失速过程，为对转压气机的进一步应用提供支撑。