三通道登机桥的运动分析及动力学计算
2022-01-10罗良清谭朝阳顾晓勤
罗良清,谭朝阳,顾晓勤
三通道登机桥的运动分析及动力学计算
罗良清1,谭朝阳2,顾晓勤2
(1.灏博生态科技(广东)有限公司,广东 中山 528400;2.电子科技大学中山学院,广东 中山 528402)
考虑登机桥外通道和中通道的运动约束关系,研究三通道登机桥系统7个旋转运动副和3个平移运动副,建立运动学模型。研究登机桥立柱升降运动、驱动轮电机与接机口的三个平移自由度之间的关系。接机口控制电机转动实现调整接机口姿态。建立登机桥多体系统动力学控制方程,对于接机口给定的位置运动规律,计算出升降立柱液压油缸的驱动力,以及两个行走轮驱动力矩。推导得到登机桥驱动轮的抱闸力矩计算公式。对个别重要的间歇较大的转动副进行切向力、法向力计算,计算间隙滑动移动副的接触力。针对某型号登机桥进行实际计算,得到地面提供的垂直于通道的摩擦力、立柱液压缸升力、接机口移动距离以及驱动力矩变化规律等。
登机桥;多体系统;动力学
旅客登机桥是连接候机楼和飞机机身的一种桥梁设备,如图1所示。作为一种钢结构机电产品[1],与建筑中的桥梁结构相比,登机桥不但具有普通桥梁结构的特点,更具有机械的运动特性。登机桥安全性要求高,要能够长期稳定工作,对运动控制精度有明确规定。对台风、地震、雪灾等具有抵抗能力。
登机桥的国内生产企业主要有中集天达、蒂森克虏伯(ThyssenKrupp)中山工厂等,国外有美国的杰特威(Jetways)和斯通(Stearns),日本的三菱重工(Mitsubishi)和川崎重工(Kawasaki)。登机桥有两通道式和三通道式(图2),包括支撑立柱、旋转平台、活动通道、接机口、升降系统(提供登机桥在竖直平面的旋转运动)、行走系统(驱动登机桥伸缩和水平旋转运动)、服务梯七部分组成[2]。加上电缆输送装置、控制系统和安全辅助系统等,具有自动减速和触机停止功能。

图1 旅客登机桥系统

图2 三通道登机桥
对于复杂的机械系统动力学分析计算,为避免复杂冗长的推导分析,可以采用多体系统动力学的方法,特别是运动学、动力学和控制仿真[3],成熟的商业化计算机仿真软件,为工程设计应用提供了极有力的帮助。在建模等方面,近来不少学者进行了深入的研究探讨,并成功应用在工程实践中,受到业界的欢迎。Ye Yunguang等[4]将多体动力学仿真的深度学习模型应用于机械系统,Han Seongji等[5]基于DNN(Deep Neural Networks,深度神经网络)的数据驱动建模,对柔性多体动力学进行仿真。常园园[6]对复合振动筛进行多体动力学仿真分析,得到工程所需结果。郑鹏等[7]对RV减速器摆线针轮传动进行多体动力学研究,韩朝建等[8]提出了基于MBD/SVM(Multi Body Dynamics/ Support Vector Machine,多体动力学/支持向量机)车钩分离故障预测的新方法,娄辉等[9]对浮子式波浪能传动机构进行动力学仿真,秦志等[10]对提升钢丝绳进行多体动力学仿真以及股丝应力分析。
本文建立三通道登机桥运动学模型,考虑登机桥7个旋转运动副和3个平移运动副,其中外通道C为中通道B移动距离的2倍。登机桥立柱升降液压机构和2个驱动轮电机共计3个驱动控制装置,控制登机桥接机口的3个平移自由度。接机口姿态由接机口控制电机转动实现。本文建立登机桥多体系统动力学方程,对于接机口给定的位置运动规律,计算出立柱中间的液压油缸的驱动力,以及两个行走轮的驱动力矩。本文推导登机桥驱动轮的抱闸力矩计算公式,计算间歇转动副切向力、法向力,以及间隙滑动移动副的接触力。
1 登机桥运动学模型
采用多体系统运动学记法,刚体B,连体坐标系Oxyz,=0,1,2,…,10。与地面、立柱固定的旋转平台基座0,旋转平台1,如图2所示,内通道A记为2,内通道地板面的根部通过两个铰轴与旋转平台1相连接,可绕图2中1轴旋转,从而实现通道随立柱升降。中通道记为3,与内通道即2之间沿2方向滑移。接机口与外通道C连接,如图3所示,通道C与升降机构外立柱的框架用高强度摩擦型螺栓连接成一体,记为4。

图3 接机口
升降机构的内立柱固定在行走系统横梁上,如图4所示,记为5,位于立柱中间的液压油缸的动力推杆伸缩实现整个通道的升降,即内、外立柱沿4方向平行移动,圆筒型转轴6与行走系统5的横梁沿5方向相对旋转。驱动轮的轮轴7与转轴6沿6方向相对旋转。驱动轮8、9各由一个电机驱动,沿7轴转动,实现登机桥的进退和旋转。接机平台、接机口记为10,相对4沿4方向旋转,实现与飞机舱门准确对接。
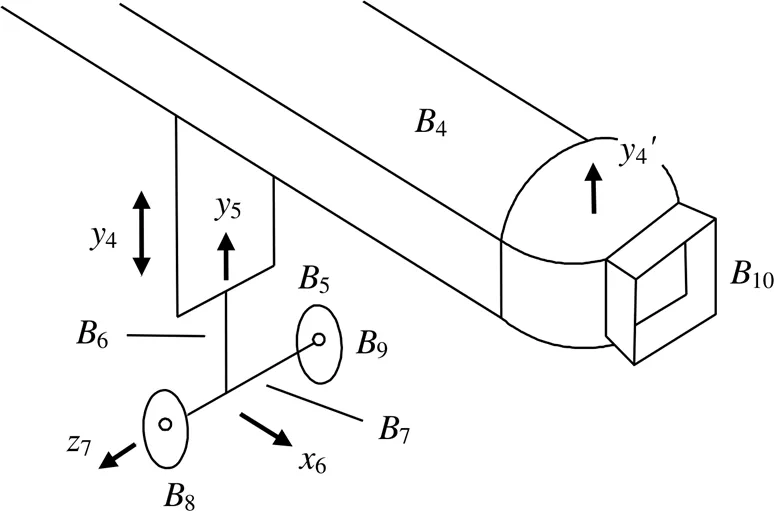
图4 行走和升降系统
登机桥系统11个刚体B(=0,1,2,…,10),相对前一个邻接刚体均为1个自由度运动,即:
1相对0,沿0轴转动1;
2相对1,沿1轴转动2;
3相对2,沿2轴滑移2;
4相对3,沿3轴滑移3;
5相对4,沿4轴滑移4;
6相对5,沿5轴转动6;
7相对6,沿6轴转动7;
8相对7,沿7轴转动8;
9相对7,沿7轴转动9;
10相对4,沿4轴转动10。
登机桥系统关联矩阵为[3]:

登机桥通道之间通过滚轮或者滑块在钢轨道上滚动或滑行,实现伸缩运动,中通道B移动速度2是外通道C速度3的一半,即3=22,结构如图5所示。一般通道的顶部与底部为折弯钢板,左右两侧由桁架、玻璃或者钢板组成。
2 动力学方程
根据文献[3],固连于刚体B的坐标系为Oxyz,基矢量为1、2、3基矢量列阵为:

转轴基矢量、滑移基矢量矩阵为:
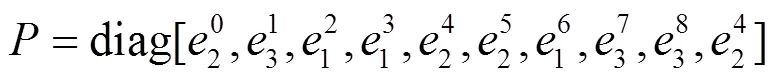
定义类型参数v:当O为转动铰时,v=0;当O为移动铰时,v=1。
则有:
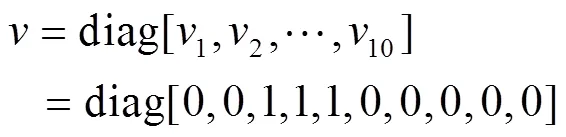
广义坐标列阵如式(5)所示。

则登机桥多体系统通路矩阵为:

设B质量m、质心C、矢径r、中心惯量张量J、角速度ω,列写Jourdain形式的登机桥多体系统动力学普遍方程,如式(7)所示。
图5 中通道B和外通道C的运动关系

构件质心矢量列阵为:

速度列阵为:

式中:为通路矩阵;′为矩阵的转置矩阵。
通道间的相对滑移速度变分为:

构件相对角速度变分为:

式中:为相对角速度变分列阵;为单位方阵。
构件绝对速度矢量列阵为:
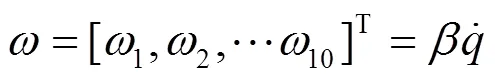
整理得登机桥系统动力学控制方程[3]为:
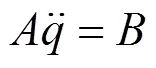
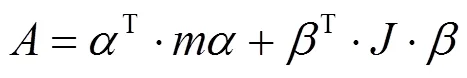


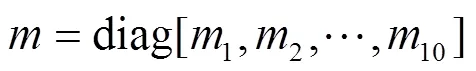


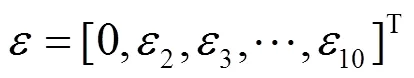
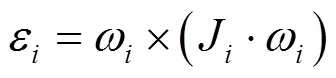
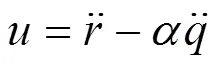



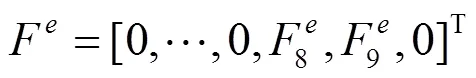
3 坐标转换

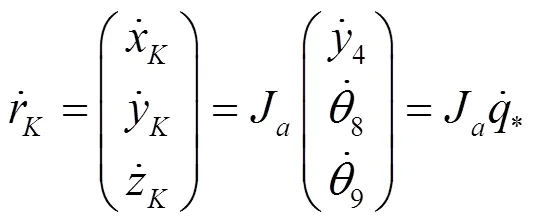
其中Jacobi矩阵[3]为:

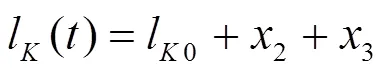
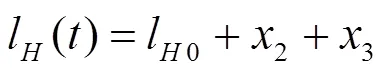

4 驱动轮抱闸力矩
当通道轴线沿1轴转动出现2不为0时,需要计算驱动轮8、9的抱闸力矩。以2<0,即4<0为例。升降立柱继续向下时,即4<0,设定其他转动铰角速度为0,1的高度0,登机桥设计制造中保证4、5与2、3垂直。登机桥橡胶驱动轮与机场地面摩擦因数大约是0.7,地面产生的最大静摩擦力完全能够阻止驱动轮8、9沿地面的相对滑移。地面对驱动轮提供的最大滚动摩阻力矩有时不足以阻止驱动轮的滚动。将驱动轮与转轴7抱闸锁定时,得到式(31)。
将式(31)对时间求一阶导数,利用3=22,得到式(32)。

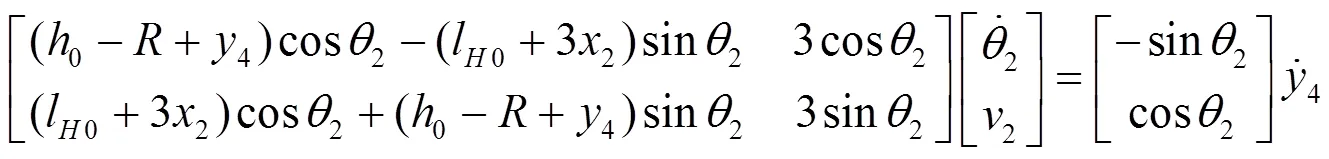
解得:
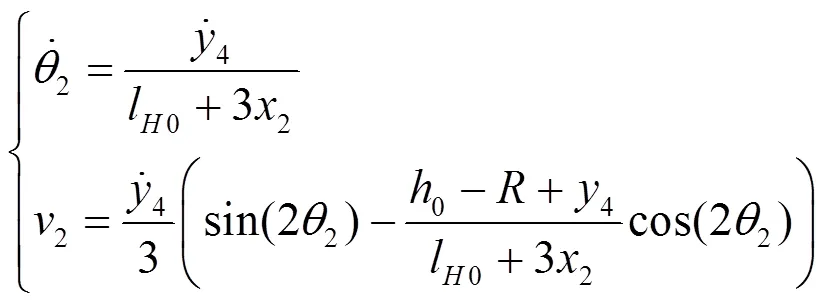

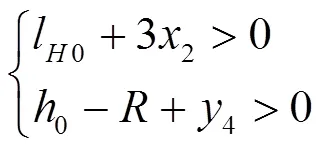
进而有:

将式(34)、式(35)代入式(33),得知登机桥通道俯仰角速度与升降立柱线速度同号。中通道B、外通道C伸缩速度与升降立柱线速度逆号。
取通道A、B、C及登机口10、升降立柱5为隔离体,由对1轴的力矩平衡方程,得到式(36)。
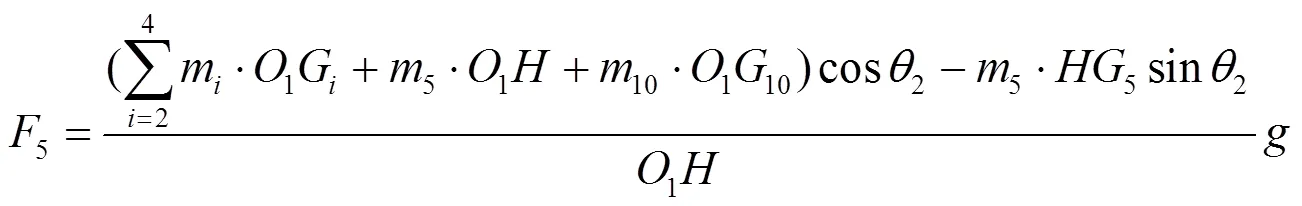
式中:1G为物体B的重心到1轴的距离,m。
驱动轮受力如图6所示,则:
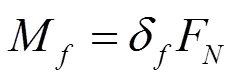
式中:Mf为滚动摩阻力矩,N·m;δf为驱动轮与机场地面的滚动摩阻因数。
驱动轮受力如图6所示,对89取力矩平衡方程,得:


5 间隙运动副接触力
对于转动铰,如果需要考虑间隙,则需要把轴承和轴两个物体分开考虑。轴在轴承中运动会出现三种情况:碰撞、非接触运动、保持接触运动。有:
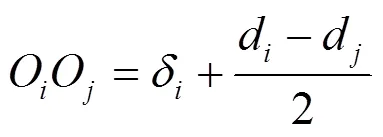
式中:OO为碰撞过程中轴与轴承的中心距,m;d和d为轴承和轴的直径,m;δ为轴和轴承的嵌入深度,m。
质心分别为C和C,在总体坐标系中位置矢量分别为r和r。轴与轴承接触点的单位法向矢量为n,逆时针旋转90°得到切向量t。相对法向速度方向确定轴和轴承是相对接近过程还是分离过程;相对切向速度确定轴和轴承是否存在相对滑动。
当轴和轴承碰撞时,发生动量交换,偏心斜碰撞,在碰撞面处产生碰撞力,将碰撞力分别向法向n和切向t投影。有:

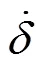
该碰撞模型只适用于恢复系数接近于1的情况。
当碰撞过程中存在相对切向运动时,会在接触面上产生摩擦力,引起切向畸变。根据库伦摩擦力定律[11],有:

式中:F为切向力,N;为摩擦系数;c为动态校正系数;v为切向速度,m/s。
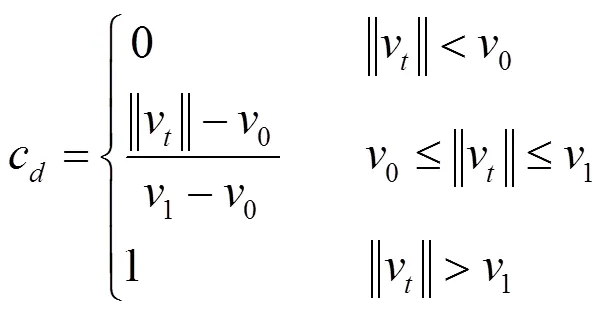
式中:0和1为切向速度的两个阈值。
移动副间隙接触状态有四种:①自由状态,滑块与导槽无接触;②滑块一角与导槽接触;③两个对角同时接触导槽;④侧面全接触。
登机桥通道之间的滑移移动副,由滚轮组成。当滑块嵌入导槽d时,由Lankarani提出的两平面线性接触力模型[11],得:

式中:F为沿y方向的力,N;为矩形接触面周长,m;v为泊松比;E为弹性模量。
6 运算求解
某型号旅客登机桥旋转平台质量1=2317 kg,对立轴中心线转动惯量1=1654 kg·m2,内通道A质量2=9139 kg,通道A与固定转台的转动副中心为1,1与旋转平台1中心线距离1=1.14 m,中通道B质量3=8277 kg,外通道C与升降系统外立柱质量4=9975 kg,接机口的质量10=2246 kg,二者质心距离410=10.75 m,行走系统及升降系统内立柱质量为2521 kg,与通道C接触点为。驱动轮直径1.12 m。设初始状态10=-5°,20=-3.5°,12=9.16 m,13=20.47 m,14=33.18 m,1=34.97 m,接机口登机点到1距离为44.93 m。伸缩过程中通道间摩擦阻力63 N。驱动轮与地面滚动摩阻系数18 mm。通道B滑动速度v=0.5C。
登机桥启动时间为10 s,按照正弦加速度运动规律(摆线运动规律),匀速运动30 s,减速时间为10 s。接机口点水平伸展速度v=0.06 m/s,上升速度v=0.03 m/s,与通道垂直的水平速度v=0.04 m/s,则登机桥通道C的滑动速度v=vcos1+vsin1,在水平面内转动摩擦阻力矩8.73 kN·m。
由以上数据得到图7~10。
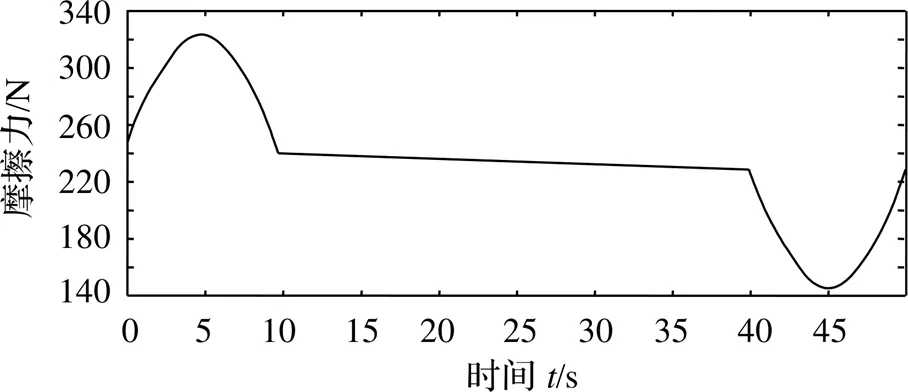
图7 地面提供的垂直于通道的摩擦力变化规律

图8 立柱液压缸升力变化规律

图9 接机口移动距离变化规律

图10 驱动力矩变化规律
7 结语
旅客登机桥在大中型机场应用广泛,对设计、制造、运输、安装、维护要求很高。本文考虑三通道登机桥7个旋转运动副和3个平行移动副,建立三通道登机桥运动学模型,进而建立登机桥动力学方程,对于接机口给定的运动规律,计算出立柱中间的液压油缸的驱动力,以及两个行走轮驱动力矩。以登机桥通道推导得到登机桥驱动轮的抱闸力矩计算公式。对个别重要的间歇较大的转动副进行切向力、法向力计算,计算间隙滑动移动副的接触力。上述工作对于登机桥运动学、动力学模拟仿真,以及细化计算,有应用价值。由于登机桥工作环境复杂,有时遇到恶劣的气候条件,机场对登机桥安全性、机电控制系统可靠性等很多方面要求非常高,所以登机桥动力学与控制方面还有待进一步细化计算、深入分析。
[1]彭恒,牛福维,顾晓勤. 集装箱运输的登机桥模块化设计[J]. 机械研究与应用,2014,27(1):107-110.
[2]顾晓勤,罗良清,袁严辉. 登机桥立柱下降中通道向上收缩的分析[J]. 机械设计,2013,30(6):40-43.
[3]刘延柱,潘振宽,戈新生. 多体系统动力学[M]. 2版. 北京:高等教育出版社,2014:60-124.
[4]Ye Yunguang,Huang Ping,Sun Yu,et al. A deep learning model for multibody dynamics simulation and its application to a vehicle-track system[J]. Mechanical Systems and Signal Processing,2021(157):107716.
[5]Han Seongji,Choi Hee-Sun,Choi Juhwan,et al. A DNN-based data-driven modeling employing coarse sample data for real-time flexible multibody dynamics simulations[J]. Computer Methods in Applied Mechanics and Engineering,2021(373):113480.
[6]常园园. 基于多体动力学的复合振动筛的仿真分析[J]. 机械管理开发,2020(12):82.
[7]郑鹏,刘晓超,赵文辉. RV减速器摆线针轮传动多体动力学研究[J]. 机械传动,2020,44(7):31-35.
[8]韩朝建,曲宝章,徐超,等. 基于MBD/SVM车钩分离故障预测的新方法[J]. 振动与冲击,2019,38(14):216-222.
[9]娄辉,张保成,赵波,等. 浮子式波浪能传动机构动力学仿真及有限元分析[J]. 工程机械,2020,51(10):30-37.
[10]秦志,黄晴,靳泓睿. 提升钢丝绳多体动力学仿真及股丝应力分析[J]. 西北工业大学学报,2020,38(3):485-493.
[11]王铁成,陈国平,马方,等. 含混合问隙多体系统动力学分析[J]. 振动与冲击,2016,35(9):178-183.
Motion Analysis and Dynamic Calculation of Three-Passageway Boarding Bridge
LUO Liangqing1,TAN Zhaoyang2,GU Xiaoqin2
( 1.Howbroad Eco-Technology (Guangdong) Co., Ltd., Zhongshan528400, China; 2.University of Electronic Science and Technology of China, Zhongshan Institute, Zhongshan 528402, China )
On the basis of the kinematic constraint relationship of the outer and middle passageways of the boarding bridge, the kinematic model of the three-passageway boarding bridge system with 7 rotational and 3 translational motion pairs is established. The relationship between the lifting motion of the boarding bridge column and the three translational degrees of freedom between the driving wheel motor and the docking part is studied. The motion of the docking port is controlled by the motor rotation. The dynamic control equation of the multi-body boarding bridge system is established, and the driving force of the hydraulic cylinder in the middle of the column and the driving torque of the two walking wheels are calculated according to the given motion law of the docking port. The lock torque calculation formula of the boarding bridge drive wheels is derived. The calculation of the tangential force and the normal force of the rotating pairs of some individual important with larger intermittent.And the contact force of the intermittent sliding pair is calculated. The actual calculation is carried out for a certain type of boarding bridge, the friction force perpendicular to the passage provided by the ground, the lifting force of the column hydraulic cylinder, the moving distance of the docking port and the variation law of the driving torque are obtained.
aerobridge;multi-body;dynamics
TH112
A
10.3969/j.issn.1006-0316.2021.12.010
1006-0316 (2021) 12-0068-08
2021-03-01
中山市科技计划项目:过山车、扶梯、登机桥结构力学计算及优化(2015B2301);中山市智能制造平台项目(26-53112203);中山市智能机器人工程中心项目(418S48);企业委托项目:可动智能设备研发(419QIQ48)
罗良清(1979-),男,江西吉安人,硕士,工程师,主要研究方向为登机桥、登船桥移动结构设计与制造,E-mail:jxlqluo@163.com;谭朝阳(1963-),女,河南许昌人,副教授,主要研究方向为多体系统动力学;顾晓勤(1963-),男,江苏常熟人,博士,教授,主要研究方向为数字化设计、仿真与制造。
