并联磁力耦合式俘能器及其特性研究

吴明轩，凌元淮

并联磁力耦合式俘能器及其特性研究

吴明轩，凌元淮

（西南交通大学 机械原理教研室，四川 成都 610031）

传统双稳态悬臂梁压电俘能器存在效率低、频带窄的弊端。为了提高俘能频带，本文提出一种并联磁力耦合式压电悬臂梁俘能装置，引入了磁力的耦合及压电片的并联。通过建立集中参数的的数学模型，使用龙格库塔数值仿真法对比分析了简谐激励下并联磁力耦合式压电悬臂梁俘能装置与单悬臂梁双稳态俘能器的运动状态及俘能特性。最后搭建实验平台进行实验验证。结果表明，磁力耦合和并联的加入，使得并联耦合式压电俘能器较传统单悬臂梁俘能器分别在7 Hz与15 Hz具有两个谐振频率，增宽了俘能器的俘能频带，以输出功率大于8×10-6W为有效频带，则俘能带宽提高约为19%。

并联磁力耦合式俘能器；压电俘能；磁力耦合；非线性；能量收集；非线性动力学

振动是普遍存在的现象。近年来随着微型机电系统（Micro-Electro-Mechanical System，MEMS）的迅速发展，从环境振动中俘获能量为MEMS供能已成为了能源收集研究领域的热点。传统蓄电池存在能量有限、电量耗尽时需要更换等弊端。压电俘能器以其微型、环保、能量密度大、自供能的特点在微电子设备应用领域得到广泛关注[1-3]。环境中的振动频率并非一成不变，例如内燃机车司机室振动随着挡位切换而改变[4]。传统双稳态悬臂梁压电俘能器效率低、频带窄，学者们为了提高俘能器的效率及带宽，开展了诸多工作。

研究表明，含非线性力的双稳态系统的动力学输出响应特性高于传统双稳态压电发电系统[5]。秦北辰等[6]通过在装置里布置矩形、梯形、三角形等多种渐变形状的发电片，实现了对自然风激励的宽频响应。高世桥等[7]设计了一种非线性双端固支梯形梁压电俘能器，降低谐振频率，提高俘能带宽及输出功率。Yonghyeon Na等[8]提出了一种基于压电双晶型悬臂梁结构的新型风能俘能器，实验表明其性能优于之前被报道的同类俘能器。S. Srinivasulu Raju等[9]提出了两种不同结构的悬臂式压电能量采集器，分别为根部是矩形截面然后是锥形截面（RTCB，rectangular section from the root followed by a tapered section cantilever beam），和根部是锥面截面然后是矩形截面（TRCB，tapered section from the root followed by a rectangular section cantilever beam），实验表明两者分别提高了91.3%和76.9%的输出电压。凌乙峰等[10]将双稳态非线性悬臂压电俘能器进行并联，仿真结果表明并联双稳态非线性悬臂压电俘能器可以有效提高俘能效率。张旭辉等[11]在臂梁式俘能结构中加入耦合磁场，仿真及实验结果表明耦合磁场的加入能拓宽悬臂梁的谐振频率。

本文提出一种并联磁力耦合式俘能器，通过磁偶极子模型建立磁力表达式，通过集中参数法建立非线性系统的动力学模型并进行数值仿真，研究对比并联磁力耦合式俘能器与单悬臂梁双稳态俘能器的运动状态及俘能特性。

1 并联磁力耦合式俘能器动力学建模

并联磁力耦合式俘能器如图1所示，两根悬臂梁固定在底座上，悬臂梁末端为大小、质量不同的圆柱形永磁铁。将两悬臂梁上的压电片并联后与负载电路连接，形成并联磁力耦合式俘能器。将非线性系统简化为弹簧－阻尼－机电耦合的集中参数模型[12]，如图2所示。将端部圆柱形永磁体质量更大的悬臂梁记为悬臂梁1，将端部圆柱形永磁体质量更小的悬臂梁记为悬臂梁2。如将悬臂梁1刚度增加到无穷大，则系统退化为传统单悬臂梁双稳态压电俘能器，此时记为单悬臂梁双稳态俘能器2。同理，将悬臂梁2刚度增加到无穷大，则记为单悬臂梁双稳态俘能器1。

图1 并联磁力耦合式俘能器示意图

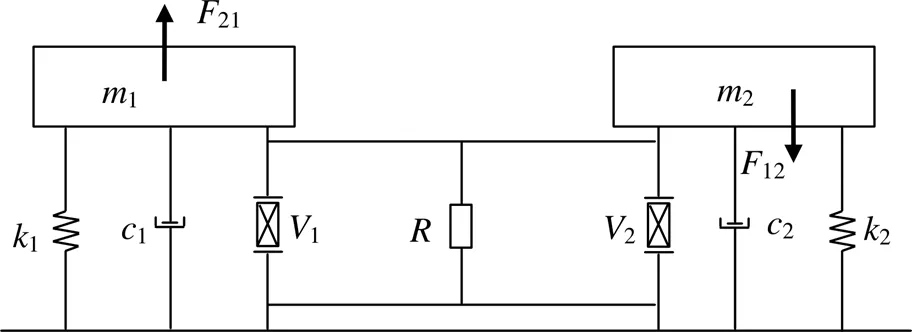
R为外接电阻，Ω；F21、F12为两永磁体的相互磁力，N；m1、m2为永磁体1、2的质量，kg；k1、k2为悬臂梁1、2自由端的等效弹性系数，N/m；c1、c2为振子等效阻尼，N·s/m；V1、V2为压电片1、2的输出电压，V。

将磁铁看作磁偶极子模型，可得式（1）[13]。

如图3所示，压电片粘贴在悬臂梁上方，在1段形成复合结构。需要将其复合界面换算为等效截面进行计算。对于A、B两种材料的复合，在假设两者间没有出现相对滑移的情况下，一般方法为将材料B按照刚度等效的原则折算为材料A，将截面特性转化为材料A的特性，在此基础上，再按照普通截面进行力学计算，可得式（2）。

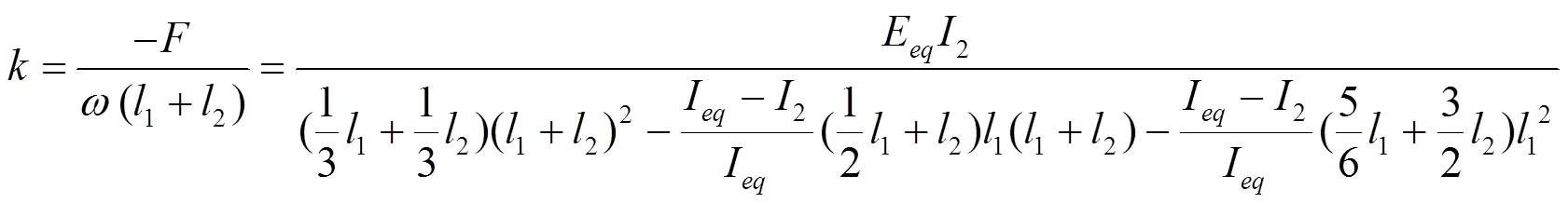
根据压电效应，当压电材料加上电压时，会产生机电耦合力F，机电耦合力对悬臂梁运动有阻碍，其大小受压电片属性影响。根据压电效应及正应力的计算公式可得：

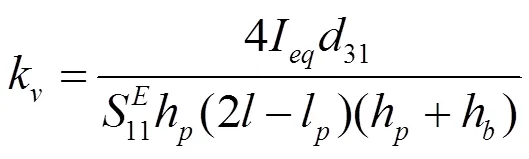
当压电片接入电路且形成通路时，压电片两端面的电场强度3＝0，由压电方程可得：

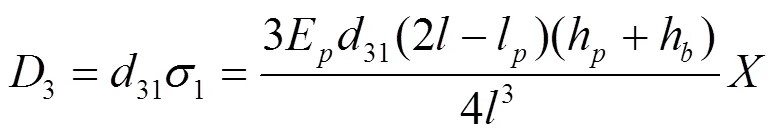
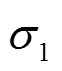
则：

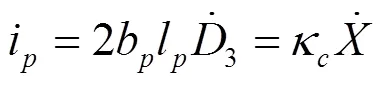
系统的等效电路如图4所示，选取外接电阻上方的节点，根据基尔霍夫第一定律，电路中任一个节点上，在任一时刻，流入节点的电流之和等于流出节点的电流之和。因此可以得到系统的电学方程为：

式中：为外接电阻两端电压，V；C1、C2为压电片1、2的等效电容，F。

考虑质量块受力情况。质量块受磁力、阻尼力、弹力和机电耦合力，由牛顿第二定律得：

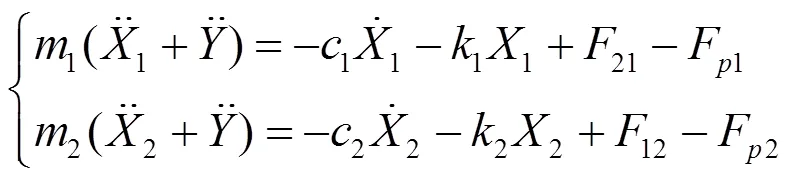
式中：Y为外界振动的函数，m；Fp1、Fp2为压电片1、2的机电耦合力，N。

联立式（6）、式（7）得系统动力学方程：

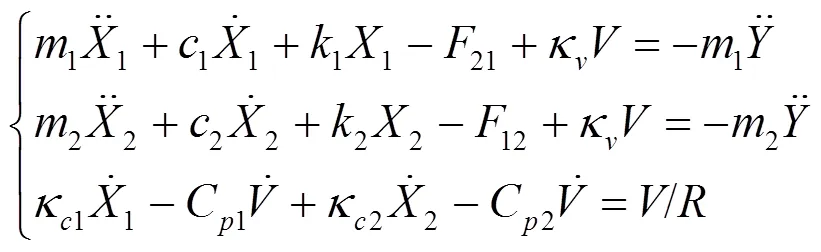
去掉磁力耦合项及并联项得传统双稳态悬臂梁压电俘能器动力学方程为：

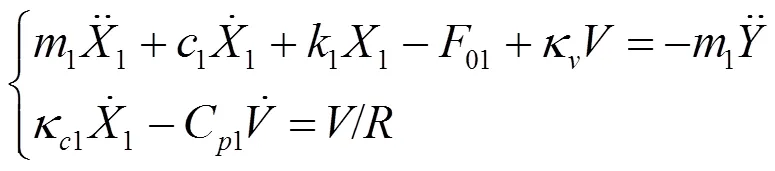
2 动力学研究

压电片材料选用PZT-5H，基底材料选用磷青铜，永磁体材料选用汝铁硼，相关参数如表1～3所示。式（8）、式（9）代入物理参数后，使用Python中scipy.integrate模块通过Runge- Kutta methods进行数值仿真。

2.1 俘能器初态的计算

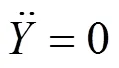
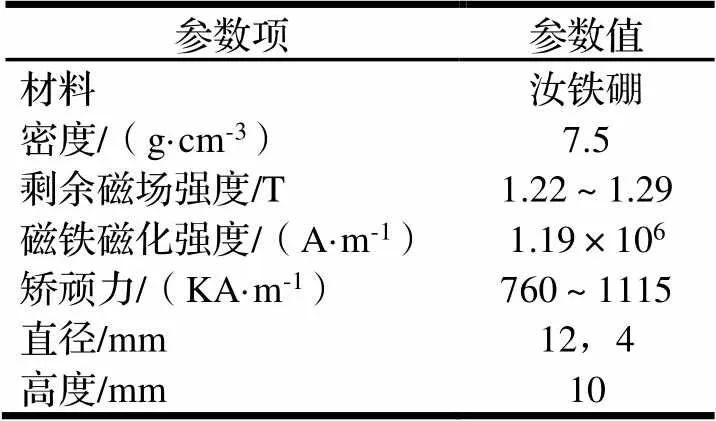
表1 永磁体参数

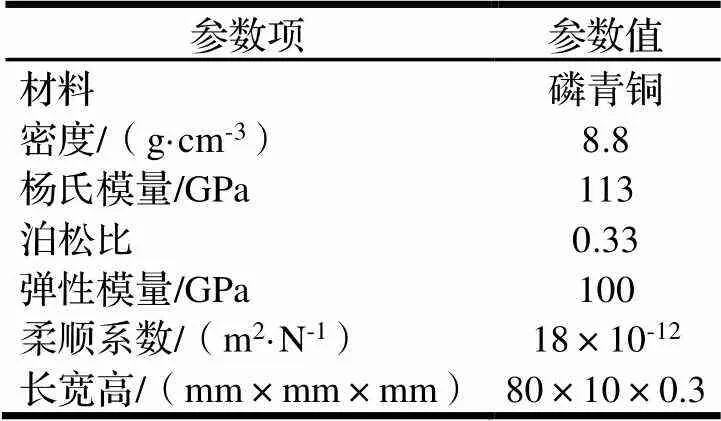
表2 悬臂梁基底参数

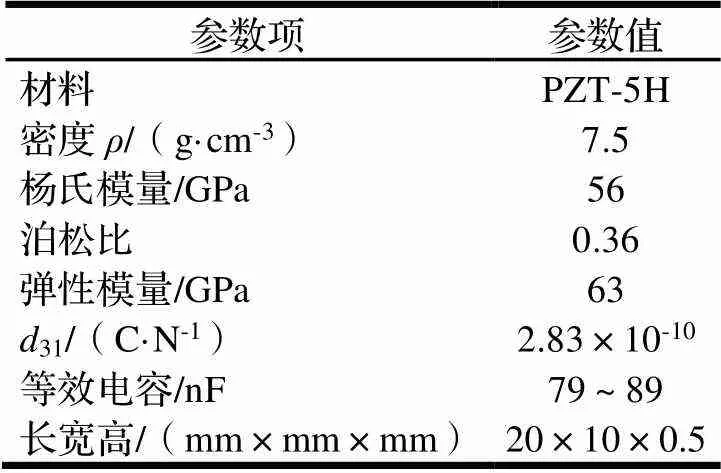
表3 压电薄片参数

注：31为压电片的一个参数。

2.2 简谐运动下的俘能特性

取＝cos(2π)、＝2 mm、＝40 mm、＝0.7 MΩ，即外界振动为简谐运动对俘能器的俘能特性进行分析。采用比较常见的方法，使用系统输出功率为指标评价俘能器的俘能效果，计算为：

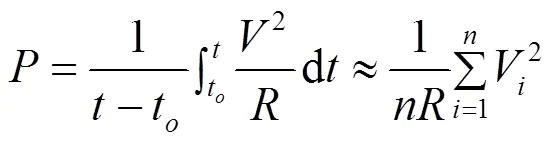
式中：为系统输出功率，W；为采样个数。

分别绘制并联磁力耦合式俘能器和两个单悬臂梁双稳态俘能器的-图像，如图5所示。

可以看出，并联磁力耦合式俘能器相较于传统单悬臂梁双稳态俘能器具有两个谐振频率。分别在在7 Hz和13 Hz处。如果以输出功率大于8×10-6W为有效频带，则并联磁力耦合式俘能器的俘能带宽为6.9 Hz，单悬臂梁双稳态俘能器1与单悬臂梁双稳态俘能器2的俘能带宽之和为5.8 Hz。俘能带宽提高约19%。进一步，绘制并联磁力耦合式俘能器的位移时域图、相图及电压时域图，如图6所示。

图5 Ω-P图像

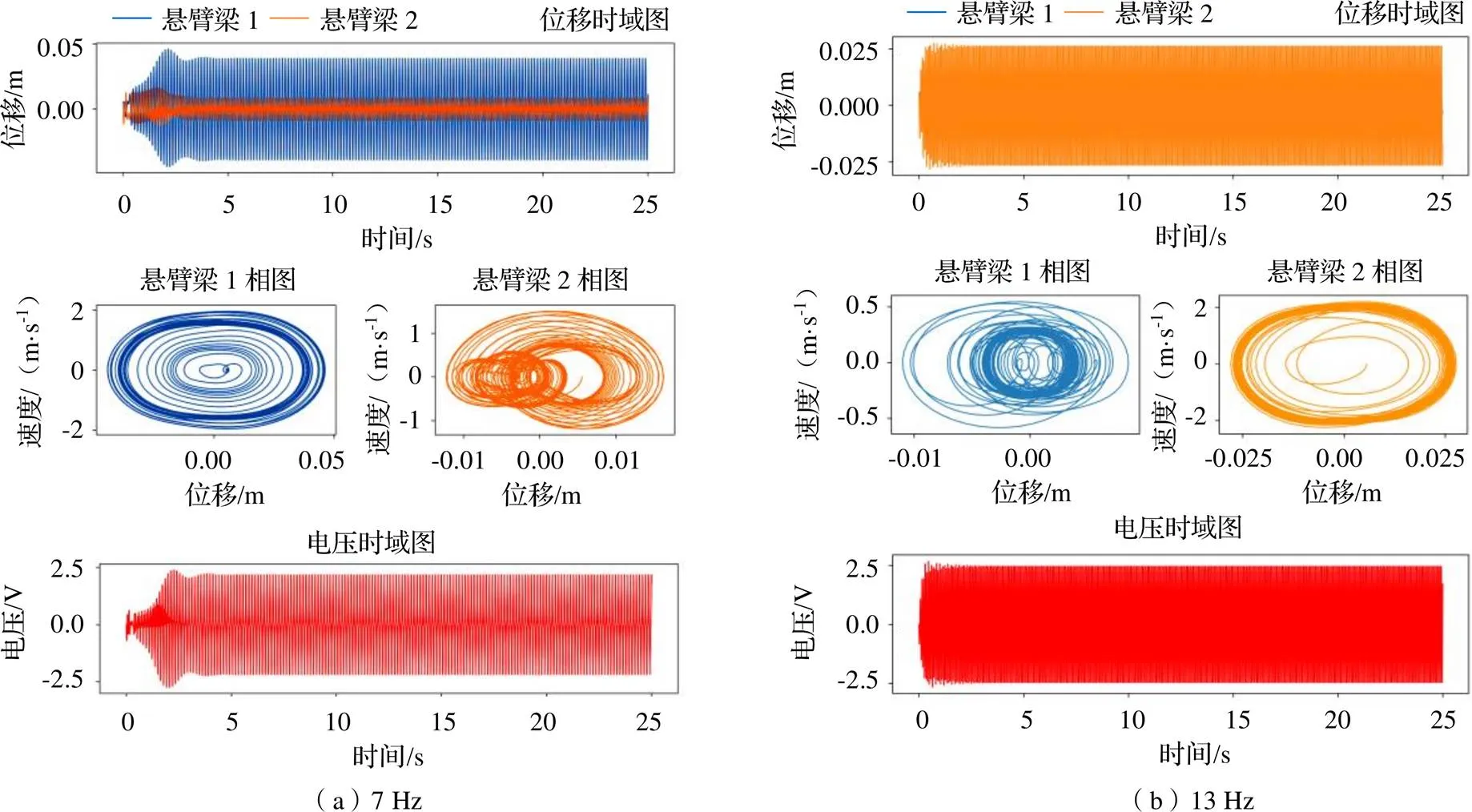
图6 并联磁力耦合式俘能器响应图

由图6可知，在7 Hz时，悬臂梁1做大幅度周期运动，悬臂梁2做拟周期运动；在15 Hz时，悬臂梁1做小幅运动，悬臂梁2做大幅周期运动。

2.3 激励幅值对俘能效果的影响

为研究激励幅值对系统俘能效果的影响,取磁铁间距40 mm、负载电阻0.1 MΩ、激励频率7 Hz，绘制并联磁力耦合式俘能器与单悬臂梁双稳态俘能器1的激励幅值与输出电压均方根关系，如图7所示。

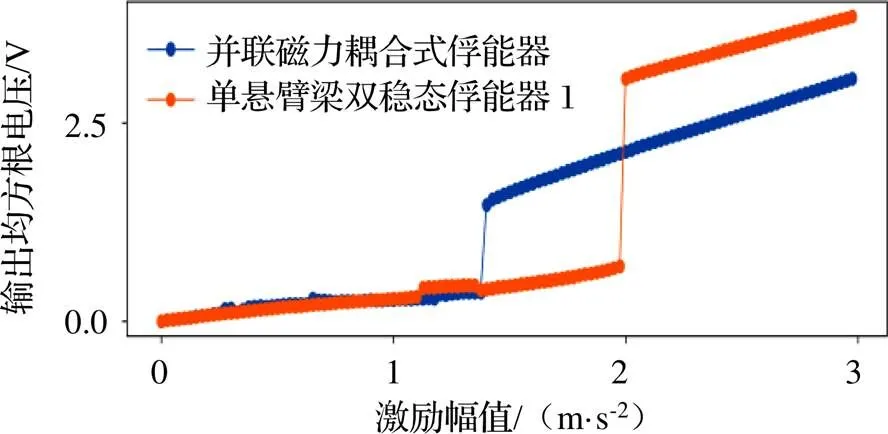
图7 激励阈值图

可看出，随着激励幅值增加，本文提出的并联磁力耦合式俘能器与单悬臂梁双稳态俘能器1的输出电压均方根均增加。并联磁力耦合式俘能器输出电压均方根在激励幅值1.4 m/s2处发生一次阶跃，单悬臂梁双稳态俘能器1输出电压均方根在2.0 m/s2处发生一次阶跃。产生这种跳跃的原因是当激励幅值较小时，传入俘能系统的能量不足以使系统越过势垒，此时悬臂梁只能在势陷内做小幅运动，输出电压小；随着激励幅值继续增加，传入俘能系统的能量增加，当传入能量足以使系统越过势垒时，悬臂梁开始做势间运动，输出电压产生阶跃。

取激励幅值1 m/s2、2 m/s2分别绘制时域图及相图，如图8所示。可看出，当激励幅值为1 m/s2时，未发生阶跃，此时悬臂梁在势陷内做小幅运动，运动幅值不超过5 mm；当激励幅值为2 m/s2时，并联磁力耦合式俘能器的悬臂梁1开始做大幅周期运动，运动幅度约50 mm。

当激励幅值超过激励阈值时，俘能器将产生大幅度响应，而并联磁力耦合式俘能器相较于传统双稳态悬臂梁压电俘能器具有较低的激励阈值。这表明在较低的激励幅值下，并联磁力耦合式俘能器拥有较好的俘能效果。

2.4 负载电阻对俘能效果的影响

负载电阻对系统俘能特性起着十分重要的作用。为分析外接负载对输出响应的影响，取激励频率5 Hz、＝2 mm、外接负载0～2 MΩ，绘制电压响应以及功率响应曲线如图9所示。由图9（a）可以看出，在0～0.3 MΩ，输出电压随着外接电阻的增加而急剧增加，之后当外接电阻继续增加时，输出电压也继续增加，但增加速率明显降低；由图9（b）可以看出，输出功率随着外接电阻的增大先增大后减小，在0.3 MΩ左右达到最大输出功率。输出功率＝2/，在0～0.3 MΩ，输出电压的平方增长速度大于外接电阻的增长速度，因此输出功率在此区间增加；在0.3 MΩ后，输出电压平方的增长速度开始减慢至小于外接电阻的增长速度，因此输出功率在此区间减小。

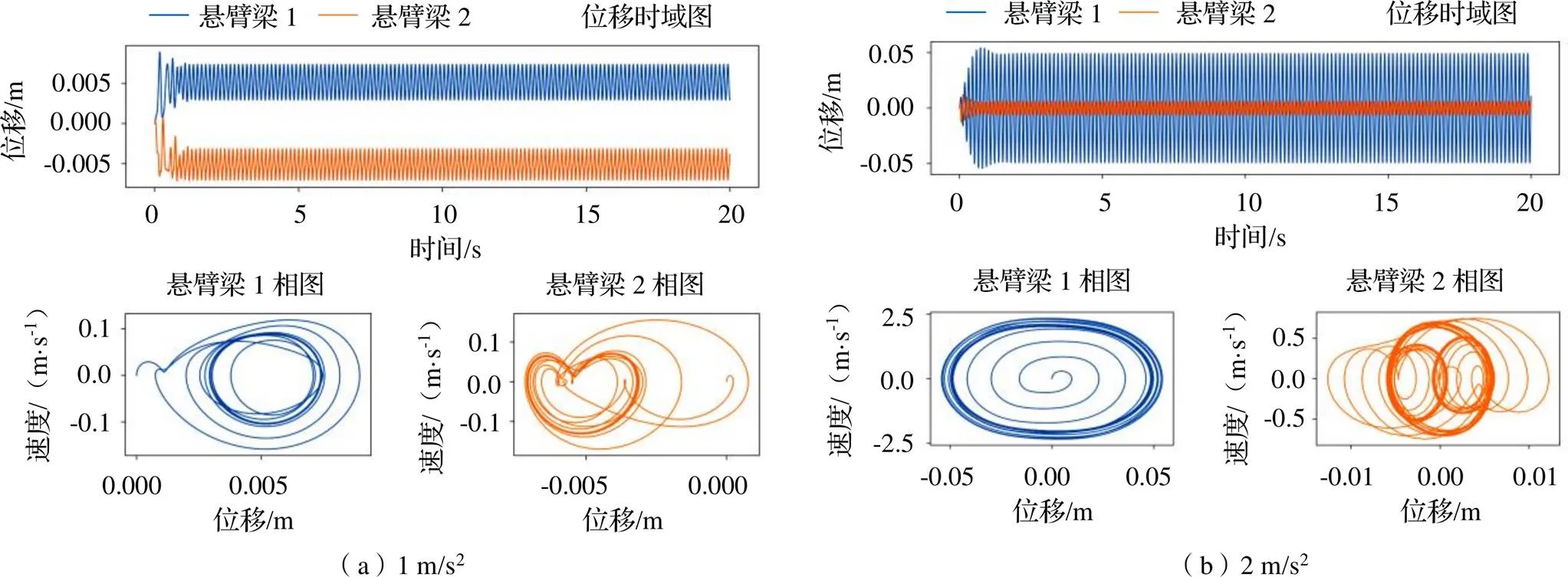
图8 并联磁力耦合式俘能器时域图及相图

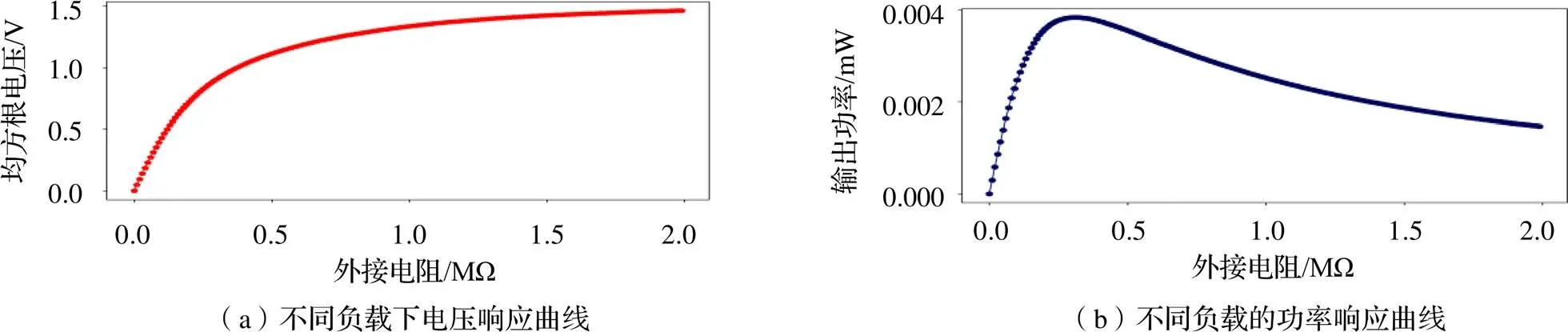
图9 外接电阻对俘能的影响

为进一步分析不同外接电阻对俘能特性的影响，取＝2 mm、＝40 mm，分别令＝0.1 MΩ、0.3 MΩ、0.5 MΩ、0.7 MΩ，作出系统的频率响应曲线，如图10所示。

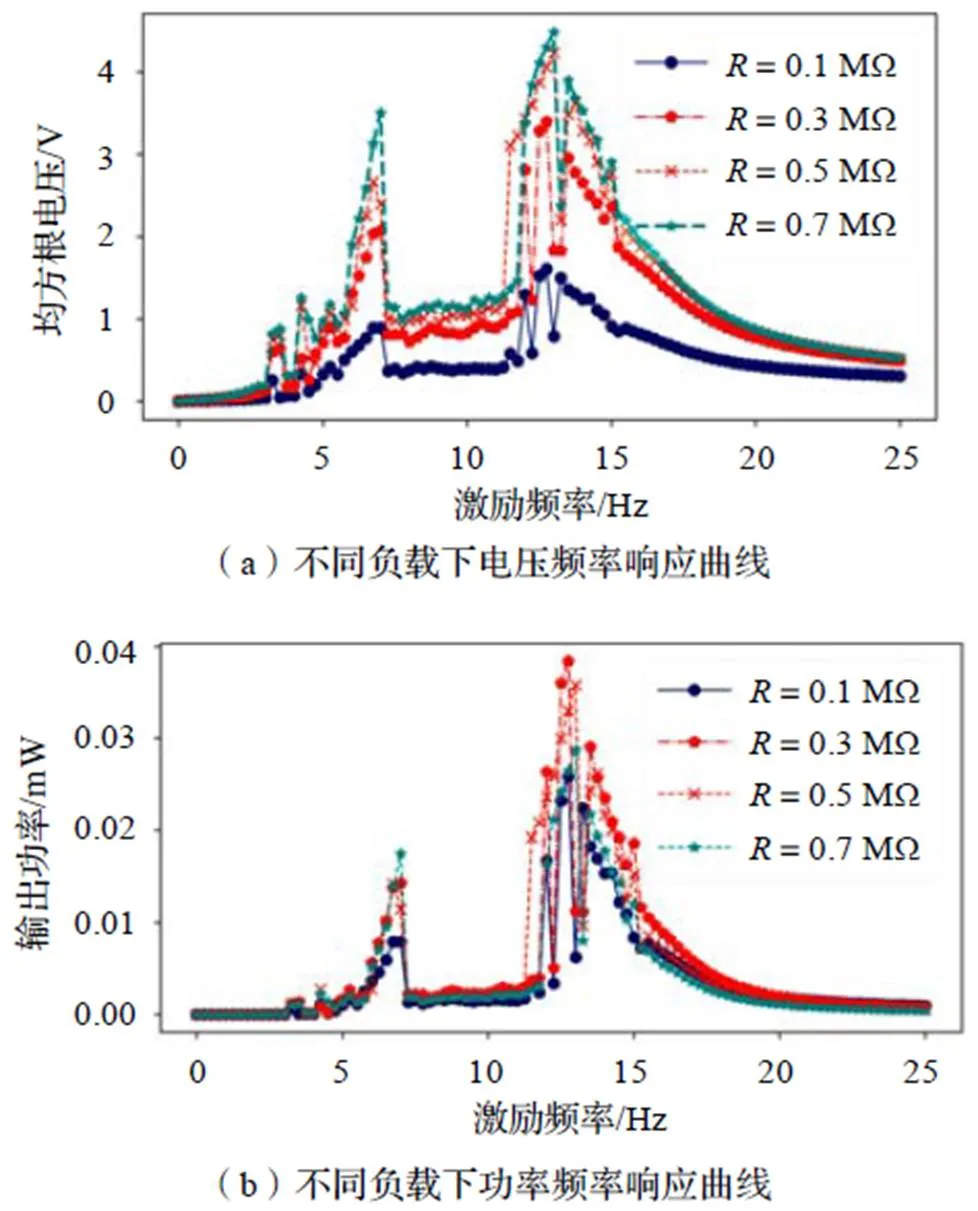
图10 不同电阻下系统的频率响应曲线

由图10（a）可知，当负载电阻＝0.1 MΩ时，输出电压两侧峰值较低，当负载电阻增大到0.3 MΩ时，输出电压有了较大提升，左侧峰值提升1 V左右，右侧峰值提升2 V左右，电阻从0.3 MΩ增大到0.7 MΩ，输出电压并未有明显提升；由图10（b）可知，当激励频率在7 Hz附近时，＝0.7 MΩ对应的输出功率峰值最大，当激励频率在13 Hz附近时，＝0.3 MΩ对应的功率峰值最大，由此可说明，随着激励频率的改变，系统最高输出功率对应的负载电阻也会发生改变。当外界激励与外接负载发生变化时，系统的运动状态随之改变，因此，不同的激励条件下系统具有不同的最佳负载，选择合适的负载电阻可有效提高系统的输出。

2.5 磁间距对俘能效果的影响

磁间距主要影响系统的势能函数，当磁间距过小时，会使势垒增高，但在高势垒下，如果越过势垒，会得到幅度大的响应和更大的电压；当磁间距过大时，由于磁力的非线性，此时磁力几乎为零，系统双方稳态消失，将难以获得大响应。取磁间距分别为35 mm、38 mm、40 mm和42 mm，＝2 mm，＝0.7 MΩ在简谐激励下绘制频率－功率曲线，如图11所示。

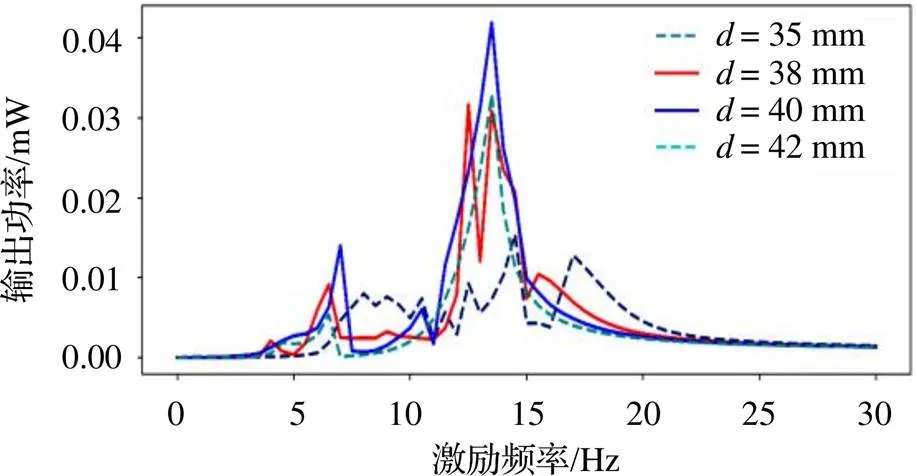
图11 不同磁间距下的输出响应

由图11可以看出，当磁间距为35 mm时，俘能器在5～20 Hz均出现响应，但响应最大值约为0.013 mW。当磁间距增大到38 mm时，俘能器在5～7 Hz及12～16 Hz出现响应，响应最大值约为0.03 mW。当磁间距继续增加到40 mm时，俘能器在5～7.5 Hz及10～16 Hz出现响应，响应最大值为0.03 mW。当磁间距增大到42 mm时，相较于磁间距为40 mm时，响应带宽以及最大输出响应均减小。可以看出，综合来说，简谐激励下，俘能器在＝40 mm时，表现出较好的响应特性。

悬臂梁的响应根据运动是否越过势垒，主要可以分为两大类，分别是陷间运动和陷内运动。其中陷内运动由于无法越过势垒，均为小幅运动。陷间运动可分为陷间大幅周期运动、陷间混沌运动和陷间周期运动。根据分类，悬臂梁在不同磁间距对于频率的响应可以抽象表达为图12。

由图12可以看出，在＝35 mm时，方块④最多，而方块①②最少。这表明磁间距过小而磁力过大，此时在外界激励下，悬臂梁难以越过势垒而做陷内运动，悬臂梁摆动幅度小，在图11中表现为输出功率低。当＝38 mm时，方块④减少，方块②增多，表明磁力减小后，悬臂梁更加容易跨过势垒。当＝40 mm时，方块①最多，此时悬臂梁最易做大幅周期运动，在正弦激励下，悬臂梁达到最大的输出功率。当＝42 mm时，方块④消失，这表明此时磁力过小，悬臂梁将不会陷入势陷内，但相较于＝40 mm时，输出功率降低。这是因为过小的磁力将难以形成双稳态，使得位移响应降低，从而输出功率降低。

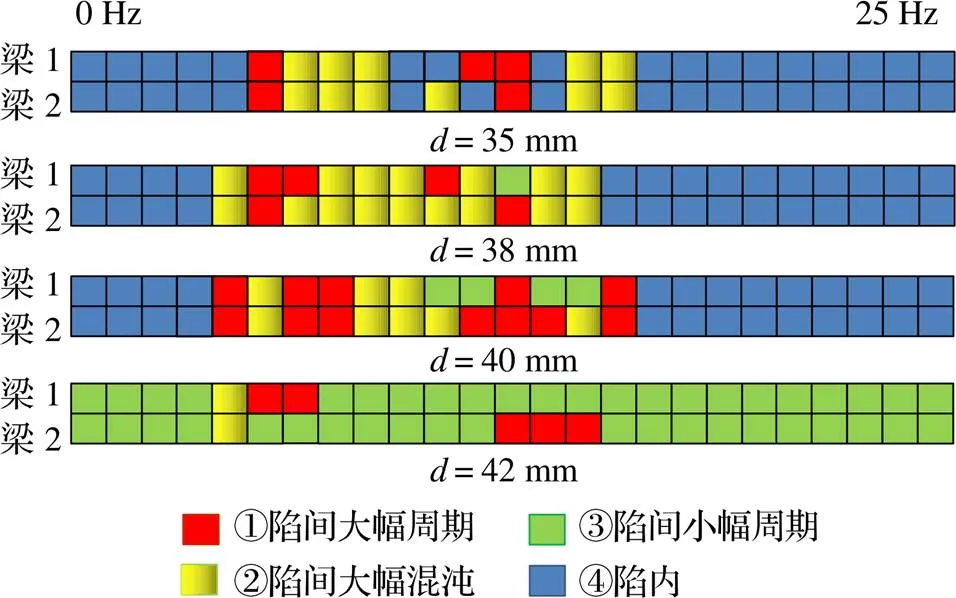
图12 不同磁间距下悬臂梁的运动状态

过小的磁间距会使得势垒过高，使悬臂梁难以越过势垒做大幅运动，此时输出功率低。过大的磁间距会难以形成双稳态，使悬臂梁不能形成大幅度响应，此时输出功率不高。选择合适的磁间距可以使输出功率达到最高。

3 实验

实验平台由激振器、信号发生器、功率放大器、并联磁力耦合式俘能器、激光位移传感器、示波器和PC组成，如图13所示。将俘能器横放以消除重力影响。实验使用信号发生器产生信号，传给激振器，产生不同频率的正弦激励，通过示波器测量俘能器的电压响应特性。

图14为俘能器理论响应特性与实验响应特性结果。

如图15所示，在频率响应实验过程中发现：6 Hz时，悬臂梁1做陷间大幅周期运动，悬臂梁2做陷间小幅运动；14 Hz时，悬臂梁2做陷间大幅周期运动，悬臂梁1做陷间小幅运动；在7～12 Hz时，两悬臂梁做陷间小幅混沌运动或小幅周期运动。实验结果与2.2节中的仿真结果一致。这是因为，悬臂梁末端的质量块质量不同，分别拥有不同的共振频率，所以存在两个峰值。实验结果与分析结果虽有一定差异，但总体趋势一致，表明所建立的模型能够较好地表征俘能器俘能特性。

通过分析，得到误差的主要来源为：

（1）数学建模上存在一些假设与简化；

（2）并联磁力耦合式俘能器的制作上存在一定误差。

图13 振动实验

4 结论

本文通过集中参数法，建立了并联磁力耦合俘能器的动力学模型。研究了并联磁力耦合俘能器在简谐激励下的俘能特性。

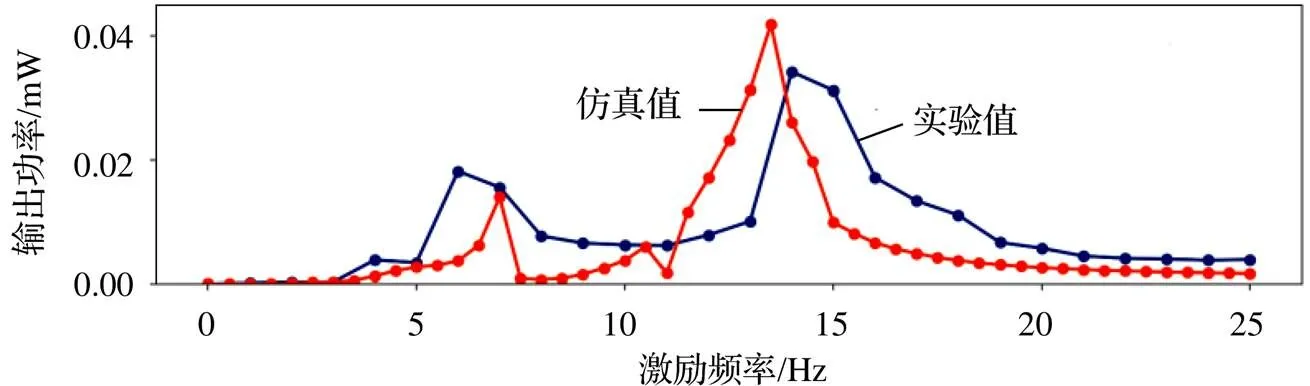
图14 实验结果

图15 悬臂梁位移时域图

研究结果表明：

（1）建立集中参数的俘能系统模型，经过实验验证，能够较好地表达出并联磁力耦合式俘能器的响应特性。

（2）磁力耦合和并联的方案，使得并联磁力耦合俘能器在7 Hz和13 Hz处存在两个谐振频率，且较单悬臂梁双稳态俘能器拥有更低的激励阈值。

（3）因为并联磁力耦合俘能器有两个谐振频率，所以较单悬臂梁双稳态俘能器拥有更好的俘能效果。以输出功率大于8×10-6W为有效频带，俘能带宽提高约为19%。

（4）并联磁力耦合俘能器的俘能效果受磁间距、外部激励频率、外部激励幅值、外接电阻等多个因素影响，各因素的影响并不是简单的促进或阻碍，而是相互耦合、共同作用。如何对俘能器进行优化值得思考。

[1]王二萍，高景霞，张金平，等. 压电俘能器研究现状及新发展[J]. 电子元件与材料，2015（9）：18-24.

[2]徐振龙，单小彪，谢涛. 宽频压电振动俘能器的研究现状综述[J]. 振动与冲击，2018，37（8）：190-199，205.

[3]王爽，吕宝占. 典型压电俘能器的发展现状与俘能机理分析[J]. 电子元件与材料，2018，37（11）：1-11.

[4]潘成，陈再刚. 不同档位下内燃机车司机室振动特性分析[J]. 机械，2019，46（10）：31-37.

[5]杨炯炯. 一种双稳态压电悬臂梁发电装置的动力学特性研究[D]. 西安：西安理工大学，2019.

[6]秦北辰，苏文斌，王春明. 宽频响应压电俘能装置设计[J]. 物理通报，2020（1）：125-129.

[7]高世桥，闫丽，金磊，等. 非线性双端固支梯形梁压电俘能器结构设计与特性分析[J]. 农业机械学报，2019，50（7）：398-405.

[8]Yonghyeon Na，Min-Seon Lee，Jung Woo Lee，Young Hun Jeong. Wind energy harvesting from a magnetically coupled piezoelectric bimorph cantilever array based on a dynamic magneto-piezo-elastic structure[J]. Applied Energy，2020，264：114710.

[9]S. Srinivasulu Raju，M. Umapathy，G. Uma. Design and analysis of high output piezoelectric energy harvester using non uniform beam[J]. Mechanics of Advanced Materials and Structures，2020，27（3）：218-227.

[10]凌乙峰，谢进，张建奇，等. 并联双稳态非线性悬臂压电俘能器的动力学与俘能特性的研究[J]. 科学技术与工程，2017（5）：218-223.

[11]张旭辉，左萌，谭厚志，等. 磁场耦合双梁压电振动俘能器响应特性研究[J]. 传感器与微系统，2019，38（12）：10-13，17.

[12]孙舒. 双稳态压电悬臂梁发电系统的动力学特性研究[D]. 天津：天津大学，2013.

[13]程建生，吴洪莉，陈义成. 两磁偶极子间的相互作用力的一种计算方法[J]. 华中师范大学研究生学报，2005（2）：130-133.

Parallel Magnetically Coupled Energy Harvester and Its Characteristics

WU Mingxuan，LING Yuanhuai

(Department of Mechanical Theory, Southwest Jiaotong University, Chengdu 610031,China)

The traditional bistable cantilever beam piezoelectric energy harvester has the problems of low efficiency and narrow frequency band. In order to improve the frequency band, a parallel magnetically coupled piezoelectric cantilever beam energy harvester is proposed. The magnetically coupling and the parallel connection of the piezoelectric plates are introduced. Through the establishment of the mathematical model of the lumped parameters, the motion state and energy harvesting characteristics of the proposed energy harvester and the single cantilever beam bistable energy harvester under simple harmonic excitation were compared and analyzed using Runge-Kutta numerical simulation method. Finally, an experimental platform was built for experimental verification. The results show that the addition of magnetically coupling and parallel connection provides the proposed energy harvester with two resonant frequencies at 7 Hz and 15 Hz respectively, compared with the traditional single cantilever beam energy harvester, which widens the energy harvesting frequency band of the device. Taking output power of more than 8×10-6W as the effective frequency band, the energy harvesting bandwidth increases by about 19%.

parallel magnetically coupled energy harvester；piezoelectric energy harvesting；magnetic coupling；nonlinear；energy harvesting；nonlinear dynamics

TH113

A

10.3969/j.issn.1006-0316.2021.12.004

1006-0316 (2021) 12-0027-09

2021-04-14

四川省科技计划项目重点研发项目（2021YFS0065）

吴明轩（1995－），男，四川内江人，硕士研究生，主要研究方向为压电俘能，E-mail：wumx1995@163.com；凌元淮（1996－），男，四川凉山人，硕士研究生，主要研究方向为送变电线路建设技术。