储能式铁路功率调节器再生制动失效抑制方案研究
2022-01-10陈利夫解绍锋黄小红王可心
陈利夫,解绍锋,黄小红,王可心
0 引言
随着我国电气化铁路[1]的加快建设,出现了许多复杂艰险山区电气化区段(如川藏铁路、西成高铁等),线路坡度最大可达30‰,坡长可达数十公里[2]。列车在上坡时所需牵引功率较高,取流较大,造成牵引网电压降低;列车在下坡时再生制动,向变电所反送再生制动能量,造成牵引网电压抬升。两种情况均会导致牵引网电压水平不达标,出现列车牵引功率不足和再生制动失效的问题,在供电臂末端尤为明显。同时,由于山区线路隧道占比较高,不得不采用带回流线的直接供电方式,使得牵引网阻抗较大,进一步加大了牵引网电压的波动[3]。因此,研究列车再生制动失效抑制与末端网压支撑对 提高电气化铁路的安全运行具有重要意义。
针对牵引电压水平导致的电能质量问题,传统解决方法是以并联电容器或电抗器[4]、静止无功补偿器(Static Var Compensator,SVC)[5]等无源补偿方式来补偿牵引网电压,但补偿精度不高。在实际工程中,通常通过设置有载调压开关的变压器调节供电臂首端电压,但调压范围有限[6]。文献[7]从机车的角度,调节机车四象限脉冲整流器交流侧电流的相位,使机车负荷在牵引网电压较高时吸收感性无功,牵引网电压较低时吸收容性无功,以调节受电弓处的电压,但该方法会增加额外能耗,降低电气设备利用率。部分文献研究通过优化行车组织提高牵引列车对再生制动能量的利用率,减小变电所负荷功率峰值[8,9],但该方法未从根本上解决列车再生制动失效的问题。随着电力电子技术的发展,以静止无功发生器(Static Var Generator,SVG)[10]为代表的有源补偿技术发展迅速,不仅能实现系统供电臂较长时末端网压的补偿[11],还可解决负序和谐波等电能质量问题[12]。但SVG不能实现再生制动能量的储存与负荷的削峰填谷。
储能式铁路功率调节器(Energy Storage Railway Power Conditioner,ESRPC)不仅可以实现供电臂间能量的双向流动,达到牵引供电系统的功率平衡,还可储存能量,提高再生制动能量利用率、削峰填谷,在治理负序、谐波等电能质量问题方面也可发挥重要作用。已有不少学者对该装置的能量管理[13~16]、控制策略[17~19]及容量优化配置[20]等方面展开了深入研究,但其原有的能量管理策略与控制策略不能适用于以牵引网末端电压为控制目标的储能式铁路功率调节器。
在直流制式的城市轨道交通牵引供电系统中,以抑制网压抬升、抑制列车再生制动失效为目标的储能系统已有广泛研究[21~23],但在交流电气化铁路中,变电所和分区所处存在电分相,且储能装置需通过变流器与供电系统相连接,加之系统中无功功率的影响,城轨储能系统的再生制动失效抑制方案并不适用于交流电气化铁路。
为抑制列车再生制动失效、支撑末端网压、兼顾再生制动能量利用和负荷削峰填谷、提高电气化铁路运行的安全性与经济性,本文介绍置于供电臂末端的储能式铁路功率调节器的结构和主要功能,分析系统各运行模式下的能量流动特性,根据系统对无功功率的需求设计变流器工作状态及其转换方式,提出以末端网压为控制目标的有功、无功协调控制策略,并建立仿真模型,对网压波动情况下有功、无功补偿进行仿真。
1 系统结构及功能
针对因牵引网电压过高导致列车再生制动失效,以及牵引网电压过低导致列车牵引功率不足等问题,提出一种调节牵引网末端电压的综合解决方案,背靠背变流器置于供电臂末端,其交流端口分别与分区所两端供电臂相连,并在直流侧接入储能装置,构成ESRPC。系统结构如图1所示。
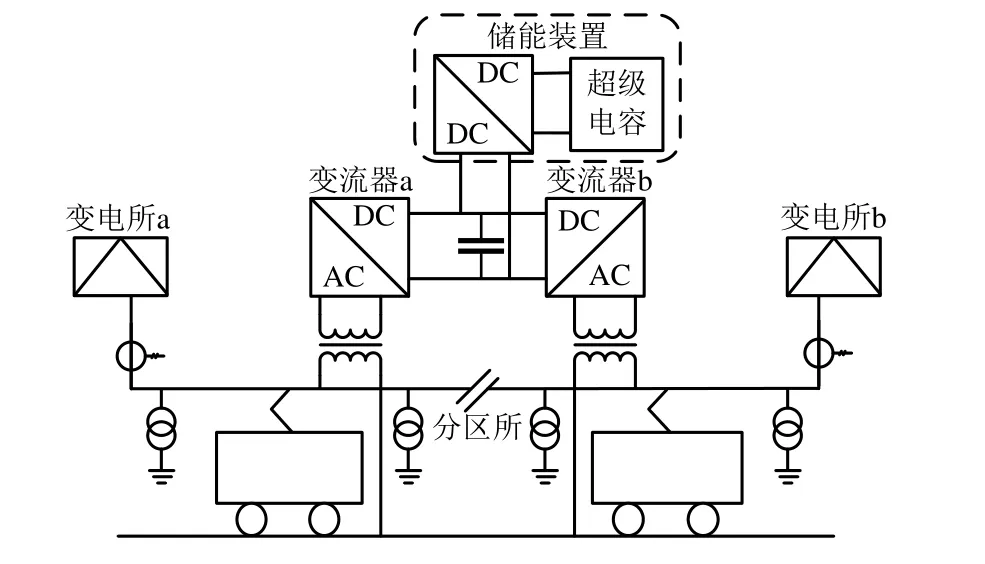
图1 ESRPC系统结构
相比置于变电所馈线出口处,ESRPC置于供电臂末端不仅能够实现两供电臂的能量流通和储能,而且能够调节牵引网末端电压。系统实时检测负荷功率的大小,控制RPC转移有功功率,储能装置储存或释放电能,减少变电所输出功率,进而稳定末端网压。此外,牵引网末端电压过高时,变流器可吸收感性无功,降低网压;牵引网末端电压过低时,变流器可吸收容性无功,抬升网压。
2 系统运行策略
2.1 网压补偿策略
列车再生制动失效的重要原因是再生制动功率过大而导致网压过高,储能装置储存并适时利用再生制动能量,降低末端网压的同时还可节约电度电费,相比于传统的无功补偿方式具有更好的经济性。有功补偿应优先于无功补偿,有功补偿和无功补偿的原则如下:
(1)ESRPC实时进行再生能量回收利用和削峰填谷,各端口功率的大小根据两供电臂负荷功率调节;
(2)在有功补偿不能使末端网压达到要求时,无功补偿延时一段时间启用,且无功补偿的大小应根据末端网压调节。
仅利用有功补偿的情况下,合理分配储能装置与两供电臂的功率,可更好地抑制列车再生制动失效,支撑末端网压,实现再生制动能量合理利用和削峰填谷,系统功率分配原则如下:
(1)优先降低负荷返送牵引变电所的再生制动功率,抑制列车再生制动失效;
(2)若无再生制动能量返送牵引变电所,则降低牵引变电所负荷峰值功率,支撑末端网压;
(3)若两供电臂需同时抑制再生制动失效,或同时支撑末端网压,根据两负荷大小的绝对值按比例分配储能装置的充放电功率;
(4)不能被同供电臂列车利用的剩余再生制动能量优先转移到异臂,若异臂牵引负荷不足以消纳,再由储能装置吸收。
2.2 系统运行模式
系统运行模式可分为6种,即牵引再生模式、再生模式、削峰填谷模式、削峰模式、填谷模式和空闲模式,根据两供电臂负荷大小及关系,划分系统各运行模式及各模式下工况,如表1所示。Pd1和Pd2分别为a臂和b臂的削峰功率阈值;Pc1和Pc2分别为a臂和b臂的填谷功率阈值;Pesm,c和Pesm,d分别为储能装置最大充电功率与最大放电功率。为避免重复讨论,牵引再生模式以a臂再生b臂牵引为例,削峰填谷模式以a臂削峰b臂填谷为例,削峰模式以Pa>Pd1、Pb>Pc2为例,填谷模式以0<Pa<Pc2、Pb<Pd2为例。
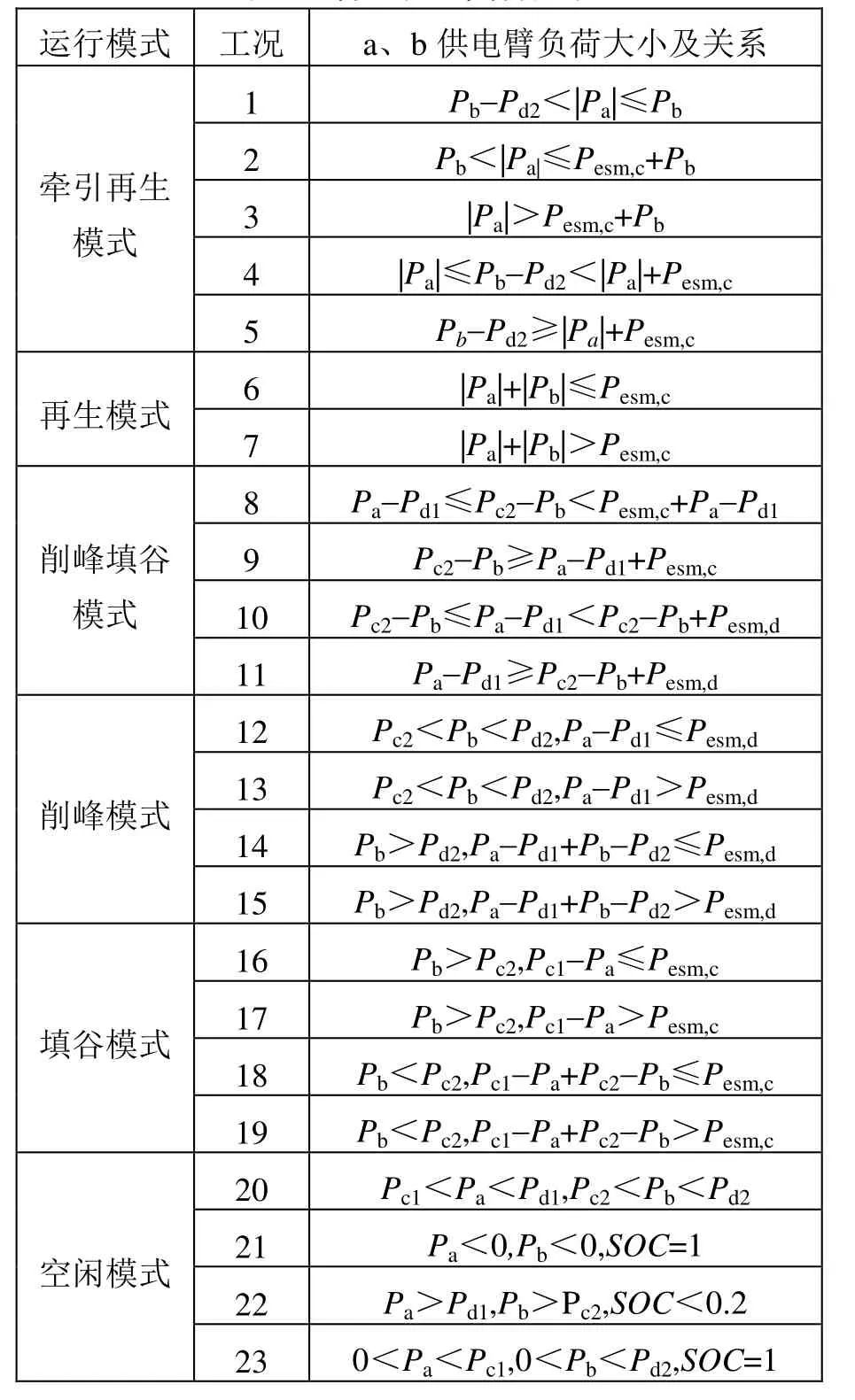
表1 各工况下负荷关系
系统运行模式转换如图2所示,根据两供电臂的负荷大小和储能装置的SOC,装置实时对系统模式进行判断,满足转换条件时进行模式转换。
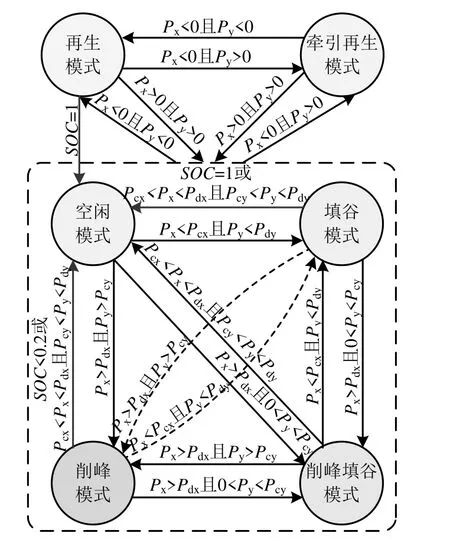
图2 运行模式转换示意图
超级电容的充/放电功率会受到其荷电状态(SOC)的限制,SOC=1时禁止充电、SOC<0.2时禁止放电[17]。因此,工况21、工况22和工况23即使满足储能装置充电或放电的条件,系统仍工作于空闲模式;在工况2、工况3、工况8、工况9下,若SOC=1,储能装置待机,系统只进行功率转移;在工况4、工况5、工况10、工况11下,若SOC<0.2,储能装置待机,系统只进行功率转移。
2.3 功率流动特性
ESRPC的功率分为3部分,即变流器a功率Pca、变流器b功率Pcb和储能装置功率Pes。规定变流器整流功率为正、逆变功率为负,储能装置充电功率为正、放电功率为负。ESRPC的功率关系可表示为

负荷功率由变电所和ESRPC两部分共同提供,a臂与b臂负荷功率分别为Pa和Pb(忽略牵引网功率损耗),牵引为正、再生为负;变电所a的功率为Psa,变电所b的功率为Psb,两供电臂的功率关系为

分别以工况2、工况6、工况10、工况14、工况18、工况20为例,对牵引再生模式、再生模式、削峰填谷模式、削峰模式、填谷模式和空闲模式进行说明。系统的典型工况功率流动如图3所示。
(1)工况2。系统处于牵引再生模式,a臂的再生制动功率|Pa|大于b臂牵引功率Pb,且小于等于储能充电装置最大充电功率Pesm,c与b臂牵引功率Pb之和,其原理如图3(a)所示。此时,b臂牵引功率完全由a臂再生功率提供,储能装置吸收再生制动能量。ESRPC各部分功率为

(2)工况6。系统处于再生模式,a臂与b臂的剩余再生功率之和(|Pa|+|Pb|)小于等于储能装置最大充电功率Pesm,c,其原理如图3(b)所示。此时,两供电臂负荷由储能装置完全吸收,供电臂间转移功率为0,ESRPC各部分功率为

(3)工况10。系统处于削峰填谷模式,a臂削峰所需功率(Pa-Pd1)大于等于b臂填谷所需功率(Pc2-Pb),且小于b臂填谷所需功率(Pc2-Pb)与储能装置最大放电功率Pesm,d之和,其原理如图3(c)所示。此时,a臂负荷功率由变电所a、变电所b和储能装置共同分担,ESRPC各部分功率为
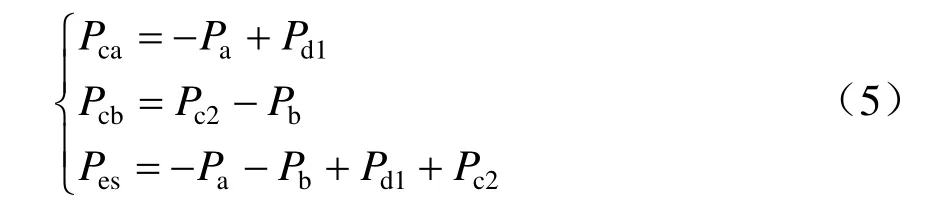
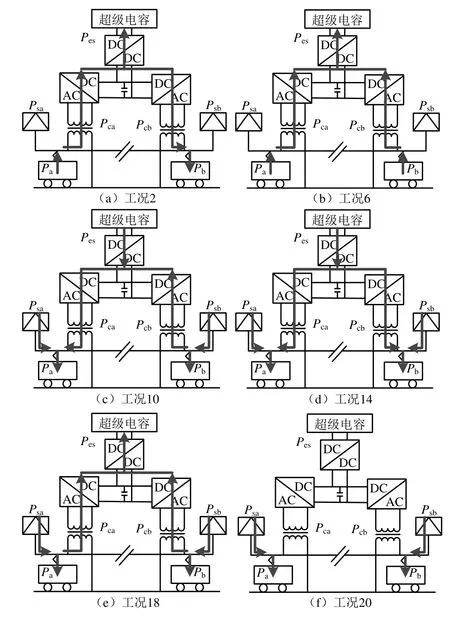
图3 典型工况功率流动
(4)工况14。系统处于削峰模式,a臂削峰所需功率(Pa-Pd1)与b臂削峰所需功率之和(Pb-Pd2)小于等于储能装置最大放电功率,其原理如图3(d)所示。此时,a臂负荷由变电所a与储能装置共同分担,b臂负荷由变电所b与储能装置共同分担,储能装置放电,放电功率为两供电臂削峰所需功率之和,ESRPC各部分功率为
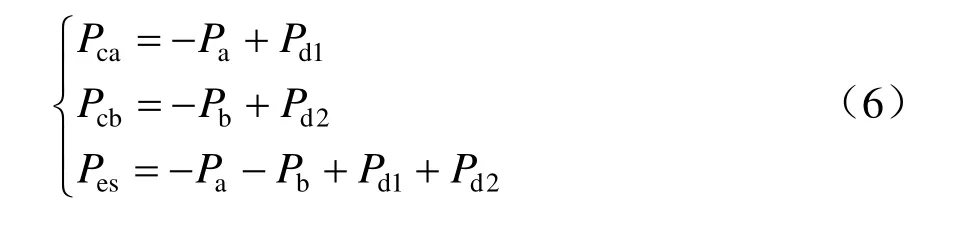
(5)工况18。系统处于填谷模式,a臂填谷所需功率(Pc1-Pa)与b臂填谷所需功率(Pc2-Pb)之和小于等于储能装置最大充电功率。此时,由变电所a和变电所b向储能装置充电,充电功率为两供电臂填谷所需功率之和,其原理如图3(e)所示,ESRPC各部分功率为
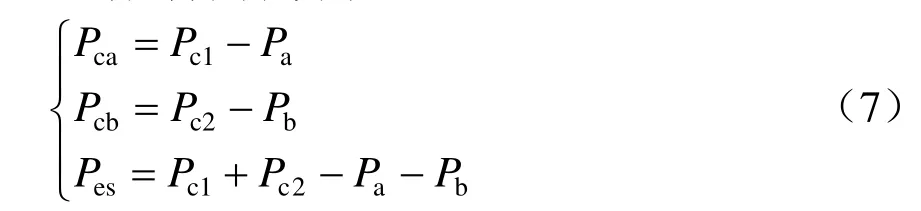
(6)工况20。系统处于空闲模式,两供电臂负荷功率均处于牵引状态,且均大于等于填谷功率阈值、小于等于削峰功率阈值,其原理如图3(f)所示。此时不需要回收再生能量、削峰填谷,装置待机,RPC和储能装置功率均为0,ESRPC各部分功率为

3 系统控制策略
为实现调节牵引网末端电压、利用再生制动能量和削峰填谷的目标,需要变流器和储能装置的协调配合,变流器a用于稳定直流侧电容的电压,变流器b和储能装置接收功率指令信号,输入输出相应大小的功率。需要控制的对象包括:(1)不同工况下变流器b和储能装置的有功功率指令信号;(2)变流器工作状态信号以及末端网压有效值参考值;(3)RPC装置两端口功率以及直流侧电容电压;(4)储能装置的充放电功率。由于控制目标较多,系统的控制策略较为复杂,因此提出分层控制策略,系统整体控制策略如图4所示。
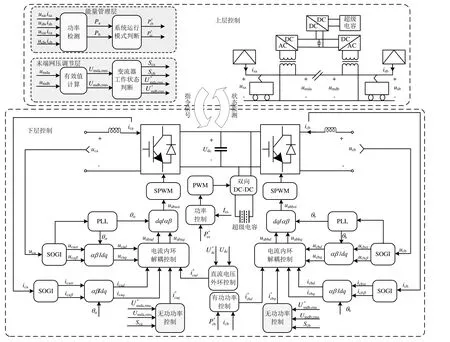
图4 系统控制原理及策略
上层控制由能量管理层和末端网压调节层组成,能量管理层包括负荷功率检测以及运行模式判断模块,末端网压调节层包括有效值计算以及变流器工作状态判断模块。下层控制包括变流器控制以及储能装置控制两部分。
3.1 上层控制
对于控制有功功率的指令信号,能量管理层检测两供电臂的负荷功率,基于第2节所述的网压补偿策略判断系统所处模式和工况,确定储能装置参考功率和变流器b参考功率;对于控制无功功率的指令信号,末端网压调节层实时采集末端网压信号,并计算其有效值,根据有效值确定变流器的工作状态以及吸收无功功率的大小。
为提高再生制动能量和削峰填谷的效果,优先利用变流器和储能装置吸收或释放有功功率,当RPC转移有功功率或储能装置不能将牵引网电压调节至正常水平时,再控制变流器吸收无功功率,实现调节网压、抑制再生制动失效。
3.1.1 变流器工作状态
为使有功功率优先补偿网压,需限制变流器吸收无功功率,继而定义3种变流器工作状态,即有功状态S0、感性无功状态S1和容性无功状态S-1,其工作状态信号Scx、变流器指令、q轴电流参考值和末端网压有效值参考值*md,rmsxU如表2所示。
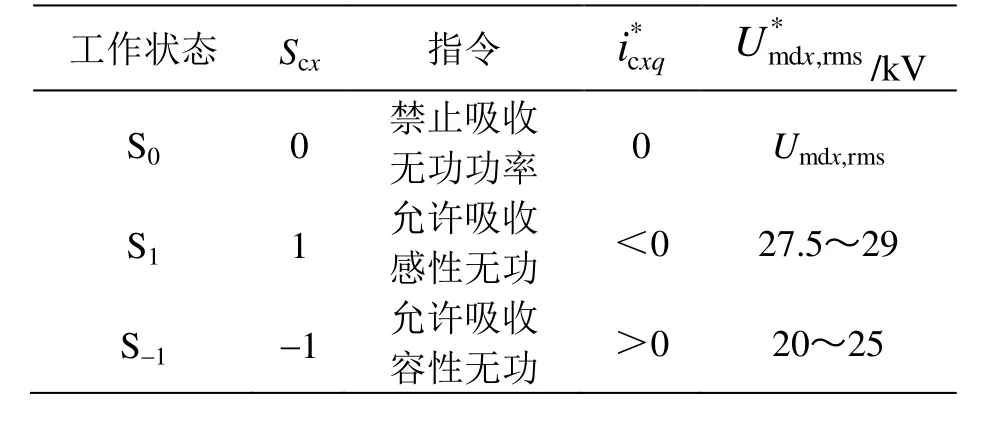
表2 变流器工作状态
表2中:*md,rmsxU为x臂(a臂或b臂)末端网压有效值参考值;Umdx,rms为x臂末端网压有效值实际值;为变流器x(变流器a或变流器b)的q轴电流参考值,感性为负、容性为正;Scx为变流器x工作状态信号。用变流器工作状态信号表示变流器所处的工作状态:当Scx= 0时,为S0状态,禁止变流器吸收无功,*md,rmsxU与牵引网末端电压实际有效值相等,即*md,rmsxU=Umdx,rms;当Scx= 1时,为S1状态,允许变流器吸收感性无功;当Scx= -1时,为S-1状态,允许变流器吸收容性无功。在3种状态下,装置依据第2节所述的能量管理策略,转移、储存或释放有功功率。
3.1.2 变流器工作状态转换
变流器工作状态转换如图5所示。变流器初始工作于S0状态,当末端网压在20~29 kV范围内,保持工作状态S0。当供电臂末端网压高于29 kV持续时间Δt(延时)后,变流器工作状态由S0转换为S1,Scx由0变为1,变流器吸收感性无功,降低末端网压。当Scx= 1且*cxqi<0时,保持S1工作状态,维持变流器持续吸收感性无功功率。当负荷再生制动功率减小,末端网压下降至参考电压Um*
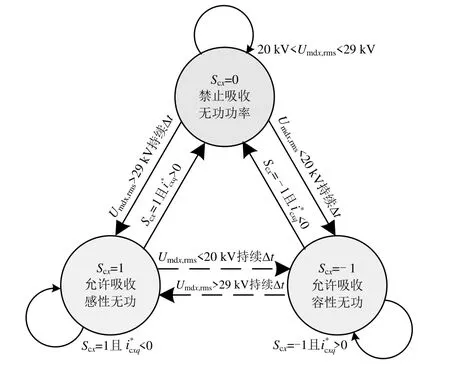
图5 变流器工作状态转换
dx,rms以下,不再需要无功补偿,变流器工作状态转换为S0。变流器S0状态与S-1状态转换过程与S0状态与S1状态转换过程类似,不再赘述。
变流器初始工作于S1状态,当末端网压有效值低于20 kV持续时间Δt后,Scx由1变为-1,变流器工作状态转换为S-1状态,吸收容性无功,提高末端网压。变流器由S-1状态转换为S1状态过程与之类似,不再赘述。
3.2 下层控制
对于有功功率控制,变流器a采用电压、电流双闭环控制,用于稳定直流侧电容电压,通过直流电压外环得到d轴电流参考值。变流器b采用功率控制,根据系统上层的指令信号,经有功功率控制得到d轴电流参考值。储能装置同样采用功率控制,根据指令信号控制储能装置充放电。
为准确地将牵引网末端电压降低到期望值,提出一种基于电压有效值PI控制的无功调控策略,即采用供电臂末端电压有效值进行无功功率控制,克服了传统给定无功指令电流控制方法[10]的不足,同时有利于再生制动能量的利用和削峰填谷。其控制原理如图6所示。牵引网将末端电压有效值的参考值与实际值作差,对差值进行PI调节,并组合变流器工作状态信号Scx产生q轴电流参考值*cxqi。
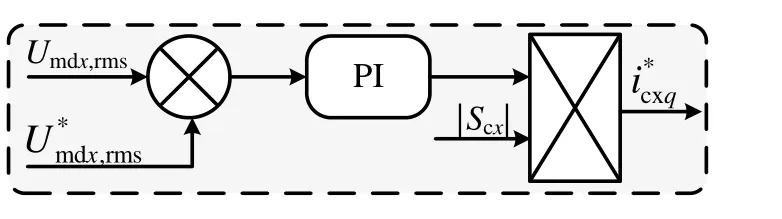
图6 无功功率控制原理
4 仿真分析
4.1 仿真参数
为了验证ESRPC对列车再生制动失效的抑制、末端网压的支撑,以及再生制动能量利用和削峰填谷的作用,搭建了带回流线的直接供电方式(DN)牵引供电系统仿真模型并进行分析,系统仿真参数见表3,网压补偿情况系统负荷仿真参数见表4。
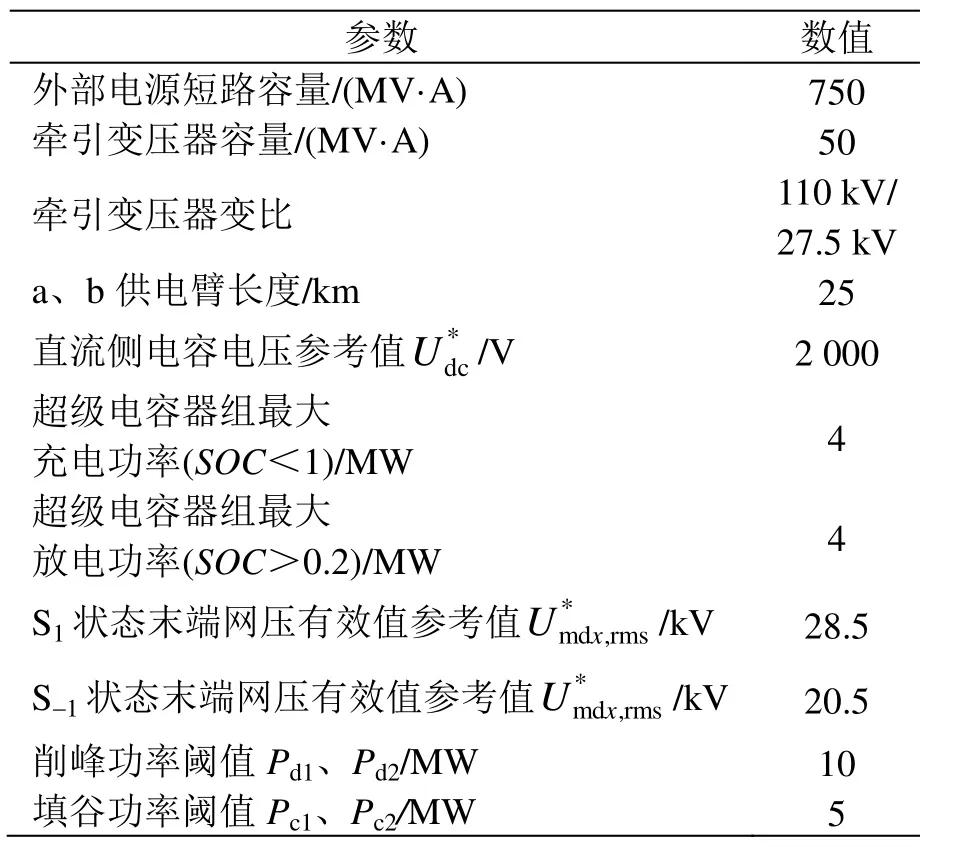
表3 系统仿真参数
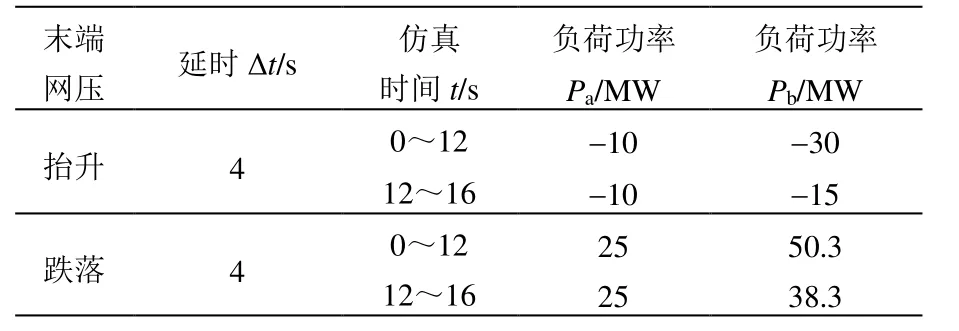
表4 系统负荷仿真参数
4.2 网压波动仿真
为验证置于供电臂末端的ESRPC抑制再生制动失效与支撑末端网压的效果,同时证明有功无功协调控制调节网压的可行性,对网压抬升和跌落两种情况进行仿真。
4.2.1 网压抬升情况
网压抬升情况仿真结果如图7所示。在0~4 s时,装置未投入,因再生制动功率过大,a臂和b臂末端网压有效值分别抬升至28.24、29.64 kV;在4~8 s时,装置启动,系统处于再生模式(工况7),两变流器均工作在S0状态,装置只吸收有功功率,Pca、Pcb和Pes分别为1、3、4 MW,两供电臂末端网压有效值下降至28.14、29.38 kV,b臂末端网压有效值仍超过29 kV;在8~12 s时,系统有功功率大小和流向不变,开启变流器b的无功补偿,其工作状态转换为S1状态,吸收2.9 Mvar的感性无功功率,并将末端网压有效值补偿至期望值28.5 kV,避免了列车再生制动失效;在12~16 s时,b臂的负荷下降至-15 MW,末端网压有效值相应降低,此时触发了变流器b的工作状态转换条件,工作状态由S1转换至S0,不再吸收无功功率,此时装置的有功功率Pca、Pcb、Pes分别为1.6、2.4、4 MW。
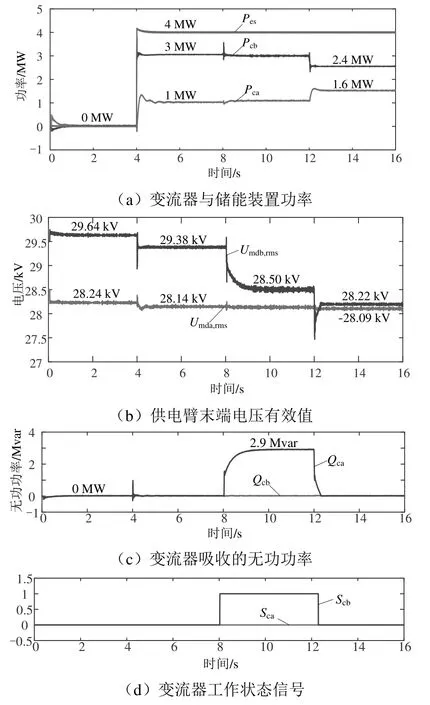
图7 网压抬升仿真结果
4.2.2 网压跌落情况
网压跌落情况仿真结果如图8所示。在0~4 s时,装置未投入,因牵引功率过大,a臂、b臂末端网压有效值跌落至21.86、19.29 kV;在4~8 s时,装置启动,储能装置开始放电,系统处于削峰模式(工况15),此时两变流器均工作在S0状态,装置只释放有功功率,Pca、Pcb、Pes分别为-1.1、-2.9、-4 MW,两供电臂末端网压有效值上升至21.97、19.58 kV,b臂末端网压有效值仍低于20 kV;在8~12 s时,系统有功功率大小和流向不变,开启变流器b的无功补偿,其工作状态转换为S-1状态,吸收2.2 Mvar的容性无功功率,并将末端网压有效值补偿至期望值20.5 kV,保障了列车牵引功率的发挥;在12~16 s时,b臂的负荷下降至38.3 MW,末端网压有效值相应上升,此时触发了变流器b的工作状态转换条件,工作状态由S-1转换至S0,不再吸收无功功率,此时装置的有功功率Pca、Pcb、Pes分别为-1.4、-2.6、-4 MW。
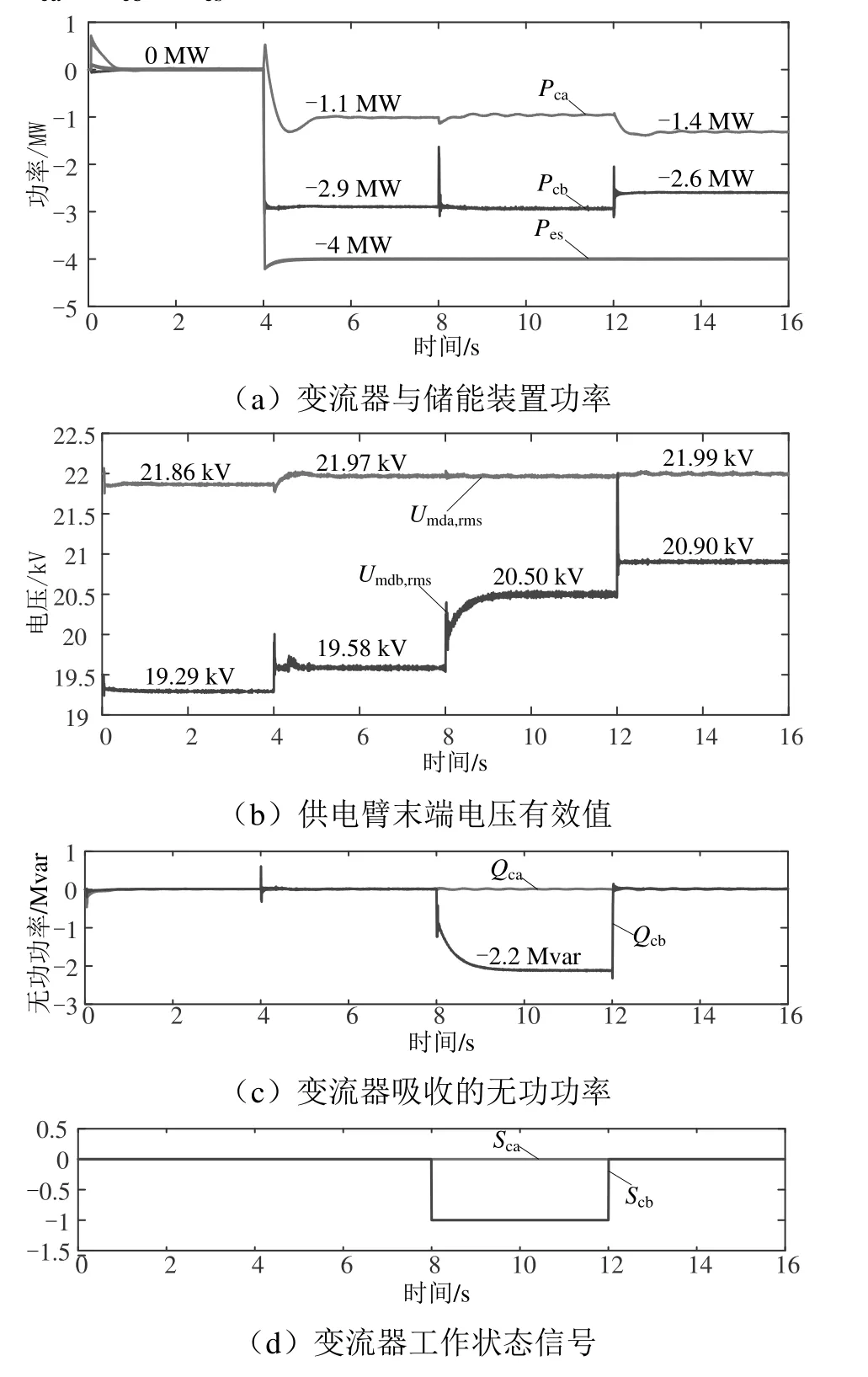
图8 网压跌落仿真结果
上述结果验证了所述方案抑制列车再生制动失效、支撑末端网压的可行性,同时验证了变流器无功控制策略的正确性。此外,在变流器吸收感性无功功率时,装置的有功功率流向及大小与能量管理策略一致,验证了前文所述有功无功协调控制方法的正确性。
5 结论
针对电气化铁路供电臂末端列车再生制动失效与网压跌落的问题,本文提出了一种置于供电臂末端的储能式RPC方案,分析其不同运行模式下功率分配情况,研究其分层协调控制策略,提出基于变流器工作状态的末端网压控制策略,通过仿真验证,得到如下结论:
(1)置于供电臂末端的储能式RPC通过有功无功协调控制,可实现再生制动失效抑制、支撑网压、再生制动能量利用和削峰填谷的功能。
(2)RPC装置两个变流器均可根据牵引网末端电压的变化实现变流器3种工作状态的切换,将牵引网末端电压补偿到期望值,实现有功功率优先补偿,无功功率有效使用。
本文主要针对基于RPC的再生制动失效抑制方案的能量管理策略以及控制策略进行研究,对于装置的容量配置、有功功率和无功功率的容量分配问题将是下一步研究方向。
