基于GARCH族模型的人民币汇率波动性研究

丁勇，葛娇娇

（中国民航大学 经济与管理学院，天津东丽 300300）

在人民币走向国际化的进程中，汇率的波动性逐渐加剧。2015年8月11日，为了增强美元兑人民币汇率的市场化程度，央行宣布再次实行人民币汇率制度改革，做市商参考前一日银行间外汇市场收盘汇率价格，向外汇交易中心进行报价。2016年10月1日，人民币正式宣布加入特别提款权，成为仅次于美元和欧元的第三大权重货币，我国汇率的波动性大大增强。2018年，在全球经济复苏、货币政策整体趋紧的大背景下，人民币汇率呈现总体贬值的态势，而2019年人民币汇率总体保持稳定，表现出了“双向波动”的特点。2020年，全球金融市场经历大幅震荡，但人民币汇率整体弹性持续增强，汇率市场化进程稳步推进。周姝彤等[1]认为人民币汇率制度市场化改革，有利于规避钉住汇率制对市场供求的扭曲以及供求失衡矛盾的积累，但亦会带来汇率波动的风险。应对人民币汇率的异常波动，朱淑珍等[2]提出应当建立人民币汇率波动监测和调节机制，实行针对人民币汇率波动的未来管理。

人民币汇率波动长期取决于我国经济基本面，而短期更易于受市场供求和国际汇市的影响[3]。随着全球金融危机影响力不断提升，以及新冠疫情这一不确定性事件对汇率的影响，汇率变化更加频繁，由此引发的汇率风险给各个行业带来较大影响。汇率大幅波动将影响到企业盈利能力甚至企业生存，汇率风险加大会影响企业投资决策，阻碍企业产率提高[4]。陈琳等[5]研究发现，人民币汇率波动增加，不仅减少了中国企业对外直接投资的可能性，也抑制了投资规模。张天顶等[6]研究发现，人民币汇率波动对上市企业出口贸易有显著的负向影响，而且汇率波动幅度越大，越不利于我国上市企业的出口贸易。对于企业来说，掌握汇率波动情况，加深对汇率波动统计特征的理解和认识，有助于规避汇率风险。因此，对于汇率波动特征的研究显得尤为重要。

许多学者以我国外汇汇率制度历史发展为出发点，分析不同时期的外汇汇率双向波动，运用GARCH族模型对人民币汇率波动规律进行了研究。骆珣等[7]应用GARCH模型对2003—2007年美元兑人民币汇率日数据进行了分析，证实了我国外汇市场确实存在ARCH效应，且GARCH模型能够较好地拟合汇改后的人民币汇率数据。刘旸[8]通过构建GARCH族模型拟合人民币汇率数据，研究发现自2005年汇率体制改革以来，汇率变化的单边趋势明显，波动幅度不断加大。2015年的汇率改革改变了原来的人民币中间价形成机制。关珊等[9]构建了GARCH模型和EGARCH模型拟合2011—2016年的人民币汇率日数据，研究发现汇率波动存在着一定的杠杆性，并针对汇率波动的影响提出了相应的政策建议。刘婷婷[10]通过EGARCH模型拟合了汇率改革之后的人民币汇率数据，同样得出收益率序列有集聚波动性、尖峰厚尾的特点，还存在杠杆效应。孙少岩等[11]应用ARIMA—GARCH复合模型进行了实证检验，研究发现我国外汇市场的中间价波动存在ARCH效应，且复合模型能够较好地拟合加入特别提款权后的人民币汇率波动规律，并对我国汇率双向波动所引起的汇率风险提出了相应的政策建议。

经对文献梳理发现众多学者对不同时期的人民币汇率波动性特征进行了研究，特别是2005年、2015年人民币汇率改革，人民币的市场化程度显著提升，新冠肺炎疫情引发人民币汇率波动增加。因此本文选取2015年汇率改革至2020年的美元兑人民币汇率日数据进行研究，通过构建GARCH族高阶模型对人民币汇率收益率的日数据时间序列进行实证分析。在考虑合适的假设分布时，选择标准正态分布、t分布以及GED分布，来拟合残差序列分布。最终综合分析各个模型参数的显著性以及信息准则，确定最优拟合模型。

1 研究方法

1.1 ARMA模型

ARMA模型是一类常用的随机时间序列模型，通常借助时间序列的随机特性描述事物的发展变化规律。如果平稳随机过程既具有自回归过程的特性又具有移动平均过程的特性，则不宜单独使用AR(p)或MA(q)模型，而需要两种模型混合使用。由于这种模型包含了自回归和移动平均两种成分，记作ARMA(p,q)，称作自回归移动平均模型，其具体形式为：

1.2 GARCH族模型

为捕捉到金融时间序列的条件异方差性以及更多的统计特征，自Engle提出ARCH模型后，各种基于Engle[12]思想的ARCH模型不断得到发展。Bollerslev[13]把ARCH模型推广到一般过程，即GARCH模型，其条件方差方程的设定为：

式(2)和式(3)中，σ2t为条件方差，Zt为独立同分布的随机变量，Zt和σt相互独立，p、q分别表示ARCH和GARCH项的次数。

GARCH模型能够很好地解释金融资产收益序列的波动聚集性特征，但是它不能解释金融时间序列经常存在杠杆效应，即负的冲击或者坏消息比正的冲击或者好消息产生的波动更大。Zakoian提出了TARCH模型以捕捉投资者对信息的非对称反应，其条件方差的设定为：

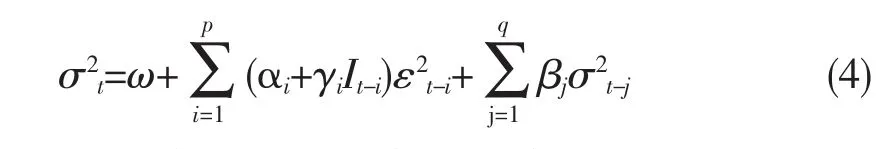
式(4)中，It-i是一个虚拟变量，当 εt-i＜0 时，It-i=1；否则，It-i=0。只要γ≠0，就存在非对称效应。好消息（εt-i＞0）和坏消息（εt-i＜0）对条件方差有不同的影响：好消息只有一个α倍的冲击，而坏消息有一个（α+γ）倍的冲击。如果 γ＞0，说明非对称效应的主要效果是使得波动加大；如果γ＜0，则非对称效应的作用是使得波动减小。

为了克服GARCH模型参数的非负性约束，Nelson提出EGARCH模型，体现出正的和负的资产收益率的非对称效应，其条件方差的设定为：

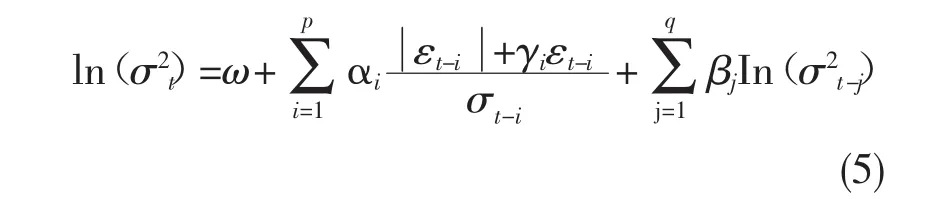
由于是对In(σ2t)建模，即使参数估计值是负数，条件方差仍然是正数。因此，EGARCH模型不需要人为假定模型参数非负数约束限制。同时，如果γ≠0，则表明存在杠杆效应；如果γ=0，则表明不存在非对称效应。

如图1所示，组合使用ARMA模型和GARCH族模型，以此提高模型的拟合优度。

图1 ARMA—GARCH族组合模型的建模流程图

2 人民币汇率波动性实证分析

2.1 样本数据的选取

为了增强美元兑人民币汇率的市场化程度，央行宣布实行人民币汇率制度改革。汇率改革之后，人民币汇率产生了较大的波动，考虑到这种情况，本文选取自2015年8月17日至2020年12月31日的美元兑人民币汇率中间价作为样本数据，共计1310个样本观测值。采用自然对数收益率的形式，即：

式(6)中，pt为第t日美元兑人民币汇率中间价，pt-1为第t-1日美元兑人民币汇率中间价。如图2所示，对数收益率时序图明显地呈现波动集束现象，即在大的波动后面紧跟着一系列大的波动，小的波动后面紧跟着一系列小的波动，大小波动有聚集现象，从而表明美元兑人民币汇率的对数收益率序列存在异方差性。

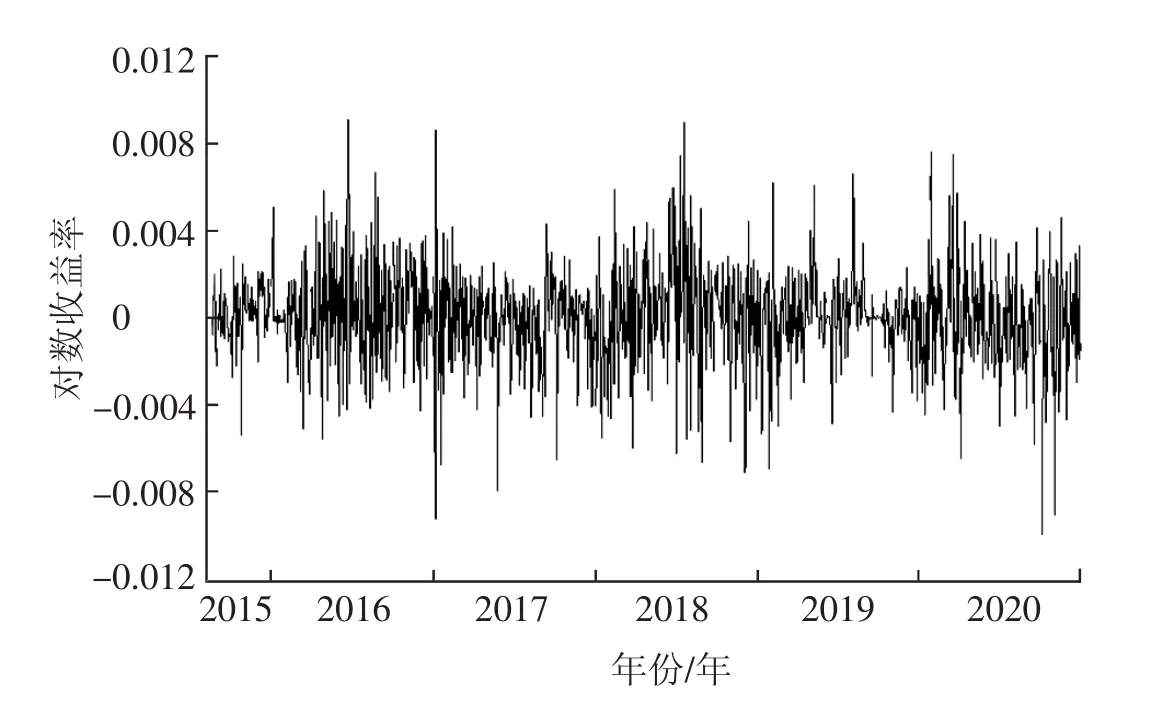
图2 对数收益率时序图特征

2.2 对数收益率的统计特征

图3统计结果表明，对比标准正态分布曲线，对数收益率存在明显的尖峰厚尾特征。因此在构建模型时，为了能够更好地拟合高频人民币汇率日数据，本文分别选择标准正态分布、t分布以及GED分布，来拟合残差序列分布。

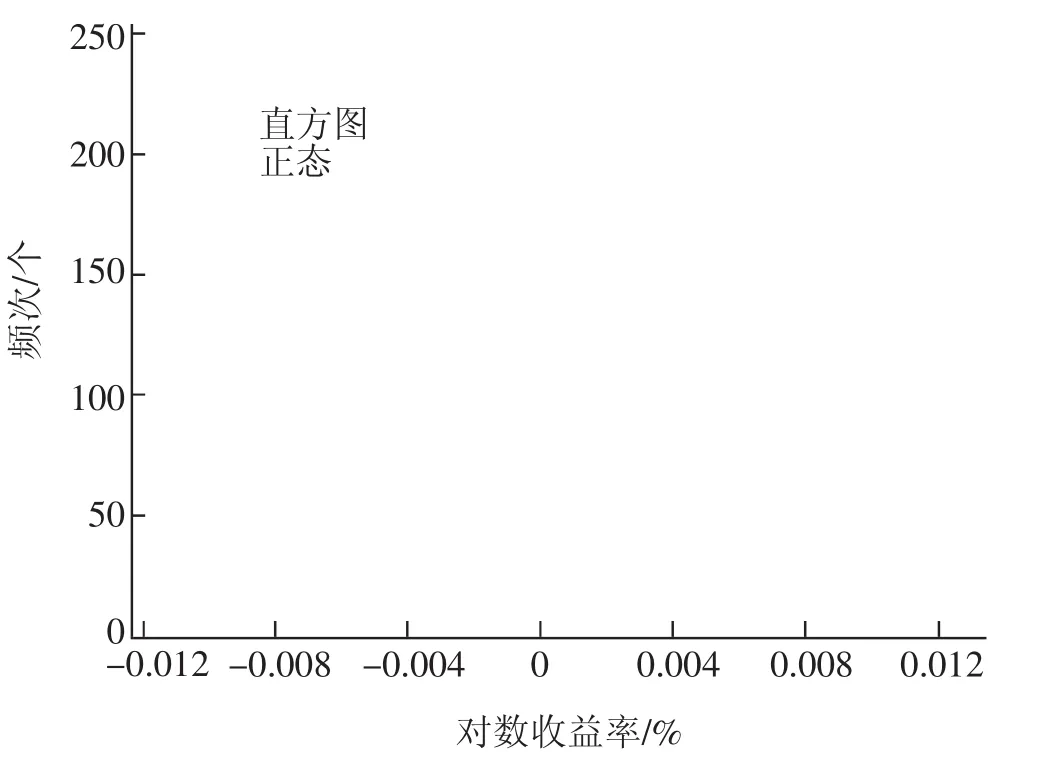
图3 对数收益率的统计特征

2.3 构建ARMA模型

2.3.1 平稳性检验

构建ARMA模型的前提是时间序列具有平稳性，因此通过ADF检验人民币汇率对数收益率序列是否平稳。由表1可知，对数收益率序列在1%，5%和10%的显著性水平下均拒绝了“存在单位根”的原假设。因此，该对数收益率序列为平稳序列，不存在伪回归的问题，可以构建ARMA模型。

表1 平稳性检验结果（ADF检验）

2.3.2 相关性检验

通过时间序列的自相关性和偏自相关性检验，可以粗略地确定ARMA模型的阶数。因此对人民币汇率对数收益率序列进行相关性检验，最大滞后阶数设为12。由表2的相关性检验结果可知，在95%的置信度下，对于低阶的自相关系数和偏自相关系数，Q统计量的P值均小于0.05，说明该序列具有明显的自相关特征。确定最优的滞后阶数，还需要通过信息准则判别各个模型的拟合结果。

表2 收益率序列相关性检验

2.3.3 ARMA模型阶数的确定

根据AIC或SC信息准则，确定最优的ARMA模型阶数，如表3所示。

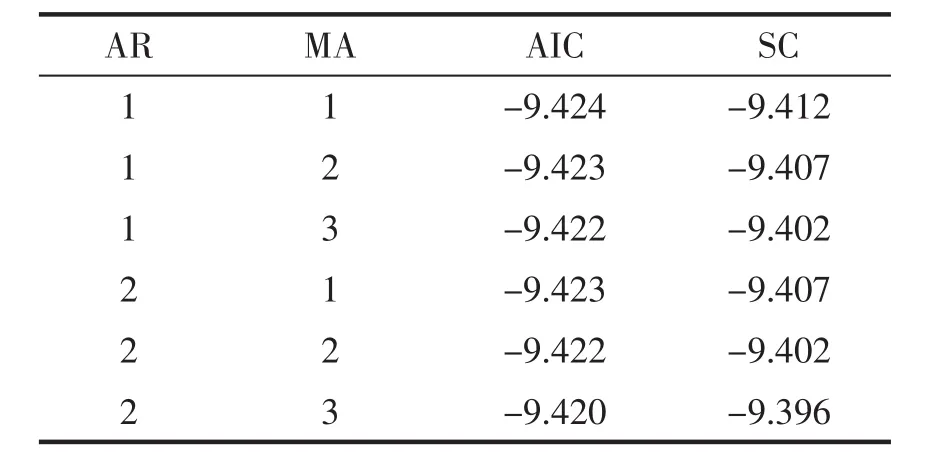
表3 ARMA模型信息准则

由表3的对比结果可知，ARMA(1,1)模型的AIC值最小，因此在构建对数收益率序列模型时，选择ARMA(1,1)模型进行均值方程的拟合最为合适。

2.3.4 ARMA模型残差检验

对所估计的ARMA(1,1)模型残差进行检验，如果残差序列不是白噪声序列，说明还存在有用的信息没被提取，需要进一步改进模型。检验结果由表4可知，残差序列的样本相关函数都在95%的置信区间内，相应的P值都大于0.05，因此不能拒绝原假设，即认为模型估计结果的残差序列不存在相关性，模型通过检验。

表4 ARMA模型残差检验

2.4 构建GARCH族模型

2.4.1 异方差性检验

建立ARMA(1,1)模型拟合人民币汇率对数收益率序列的均值方程之后，分析其残差序列是否还存在有用的信息。使用LM法检验判定残差序列是否具有ARCH效应，检验结果如表5所示。由表5可知，拒绝不存在ARCH效应的原假设，说明通过ARMA模型拟合均值方程之后的残差序列存在ARCH效应，可以构建GARCH模型拟合人民币汇率对数收益率的异方差性。

表5 ARMA模型ARCH效应检验

2.4.2 构建ARMA—GARCH模型

根据残差序列相关图，确定ARMA(1,1)—GARCH(1,1)模型刻画人民币汇率的波动性特征，估计结果如表6所示。由表6可知，在95%的置信区间内，对比不同分布假设条件，所有模型参数均显著。并且模型系数α+β＜1，满足GARCH模型的平稳性条件。

表6 ARMA(1,1）—GARCH(1,1)模型估计

但对拟合后的残差进行LM ARCH检验，P值小于0.05，故拒绝原假设，说明构建GARCH模型拟合收益率的方差方程还需要改进。考虑到金融时间序列具有非对称性和杠杆效应，因此增加TARCH模型和EGARCH模型进行对比分析。

2.4.3 构建ARMA—TARCH模型

在均值方程的基础上构建TARCH模型，估计结果如表7所示。由表7可知，在95%的置信区间内，正态分布条件下TARCH(1,1)模型和TARCH(2,1)模型，以及GED分布条件下的TARCH(1,1)模型的参数是显著的。但正态分布条件下的TARCH(2,1)模型中的a2系数为负，不符合限制条件，故排除。最后分别对正态分布条件下和GED分布条件下的TARCH(1,1)模型进行LM ARCH检验。检验结果由表7可知，P值小于0.05，故拒绝原假设，说明对方差方程构建低阶TARCH模型并不能完全提取出信息，还需要改进。

表7 ARMA(1,1)—TARCH模型估计

2.4.4 构建ARMA—EGARCH模型

在均值方程的基础上构建EGARCH模型，估计结果如表8所示。由表8可知，在95%的置信区间内，估计模型的参数均显著。首先对拟合后的残差进行LM ARCH检验，低阶的EGARCH模型均未通过检验，故排除。其次通过信息准则原理，对高阶EGARCH模型进行对比，得出GED分布条件下的EGARCH(2,1)模型能够更好地拟合数据。最后可以得到ARMA(1,1)—EGARCH(2,1)的估计结果：

表 8 ARMA（1，1）—EGARCH 模型估计

均值方程：

式(7)中，εt为服从广义误差分布，自由度为1.275。

条件方差方程：

在EGARCH模型拟合方差方程的估计结果中，非对称项的系数估计值为-0.047，小于零且统计性显著。好消息产生0.288（0.335-0.047）的冲击，坏消息产生 0.382（0.335+0.047）的冲击，从而验证了坏消息对人民币汇率波动的冲击影响更大，即存在所谓的“杠杆效应”。

2.4.5 基于最优模型的波动预测

通过拟合GED分布条件下的ARMA(1,1)—EGARCH(2,1)模型，对美元兑人民币汇率序列进行样本外预测，检验模型的预测精确程度。如图4所示，选取2021年1月4日至2021年6月30日共118个美元兑人民币汇率中间价样本数据。通过该模型对样本外数据进行动态预测后，比较美元兑人民币汇率日数据的真实值与预测值。可以发现，该模型能够较好地拟合数据，刻画汇率变化的趋势及波动性。

图4 2021年1～6月ARMA(1,1)—EGARCH(2,1)样本外预测结果

3 结论

本文通过比较不同分布假设下的模型结果得到：经过对数差分后的收益率序列是平稳序列，对其进行描述统计分析，其峰值远远大于正态分布的峰值，序列呈现尖峰厚尾分布，表明序列不服从正态分布。对序列进行自相关检验，检验结果显示存在自相关性，因此选择ARMA模型消除均值方程的自相关性。通过构建ARMA—EGARCH复合模型拟合方差方程，实证结果表明人民币汇率的波动存在杠杆效应，负面消息的冲击对于人民币汇率波动影响较大。

4 建议

回顾美元兑人民币汇率历年来的走势，汇率双向波动已然成为常态。2015年汇率改革之后，人民币汇率形成机制的市场化取得了重要进展。但新冠疫情这一不确定事件的发生，对人民币汇率波动的负面影响也更加显著。基于对人民币汇率的波动性研究，为防范人民币汇率风险提出如下建议：政府应当审慎监管人民币汇率波动情况，制定合理的人民币汇率波动区间，增强人民币汇率的弹性，稳步推进人民币汇率市场化的进程。随着人民币双向波动趋势加强，央行应当建立完善的外汇衍生品市场，为企业应对汇率风险提供灵活多样的衍生品工具。企业也应当积极应对汇率波动带来的风险，加大汇率风险管理。避免外汇风险管理的“顺周期”和“裸奔”行为，实现从被动承受外汇风险到主动应对外汇风险，从危机应对外汇风险到预警和监控的转变，进而有效规避外汇风险，降低汇率波动对企业的影响。