基于云理论的大坝整体性态评价模型

姜振翔，陈 辉，陈柏全

南昌工程学院水利与生态工程学院，南昌 330099

大坝是保障经济建设和社会发展的重要基础设施，但由于环境变化、材料老化等因素的影响，大坝在运行过程中不同程度地存在着安全隐患和失事风险[1]. 大坝一旦失事，将对下游社会造成重大威胁. 因此，采用合理的方法分析大坝安全监测系统采集的监测数据，据此评价大坝性态，对于保障大坝运行安全具有重要意义[2].

目前对大坝性态的评价工作主要包括：单测点（局部）性态评价以及多测点（整体）性态评价.对于单测点（局部）性态评价，主要采用回归算法建立单测点的监控模型，将模型计算值与测点实测值的残差作为单测点（局部）性态评价依据，当残差超过某阈值时引发警报[3-5]. 近年来，随着神经网络、支持向量机等智能算法的成熟，不少学者将其应用建立单测点监控模型，改善了监控模型计算精度[6-10]，提高了单测点（局部）性态评价结果的可靠性.

对于多测点（整体）性态的评价，目前的研究相对较少. Liu等[11]在假设监测数据服从正态分布的前提下，利用贝叶斯网络融合多测点监测数据，以置信距离测度作为评价依据，评价大坝整体性态. 何金平等[12]将大坝变形、渗流、应力应变等监测效应量视作证据体，依据专家经验对效应量赋值，经逐层融合，将欧氏距离作为表征大坝整体性态的指标. Su等[13]计算了多测点的重标极差，将其融合后，建立了基于该指数的评价模型. Yu等[14]利用主成分分析提取多测点监测信息中的主成分(PC)，将PC表征大坝整体性态，建立了PC的评价模型. 在工程应用中，通常由专家依据工程经验分析单测点监测资料，再对各测点评价结果进行定性综合，得到大坝整体性态.

综上，目前针对大坝单测点（局部）性态的评价方法已相对成熟，但多测点（整体）性态的评价方法还存在着一些不足. 主要表现为：需要借鉴专家经验，在评价过程中主观性较强. 同时还应注意到：大坝的老化、病变是一个长期、缓慢的过程，评价大坝整体性态涉及多个测点的监测资料，评价方法应具有模糊性.

针对以上问题，本文以大坝位移监测资料为基础，首先为不同测点建立了对应的监控模型，并统计各测点的残差序列. 由信息熵理论分析各测点残差的融合权重，计算融合残差. 最后将融合残差作为评价大坝整体性态的依据，通过分析融合残差的分布特征，探讨了大坝整体性态的评价准则，结合云模型理论构建了大坝整体性态评价模型.

1 评价方法

1.1 监控模型的建立

在大坝安全监控领域，监控模型描述了大坝位移与环境量之间的相关关系，是反映大坝性态的重要函数. 设坝体中位移测点数量为n，每个测点包含m次测值，当大坝具有长期监测资料时，对历史监测资料中的环境量与第i个测点实测值序列Yi(i=1,2,···,n)进行回归分析，可得到该测点的位移监控模型表达式. 已有的坝工知识表明[15]：大坝位移受水位、温度、时效等环境量共同影响，单测点位移监控模型可表达为：

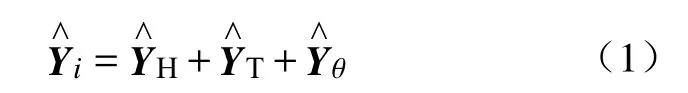
1.2 权重分析方法

单测点残差是表征大坝局部性态的关键指标，若要评价的大坝整体性态，则应同时考虑多个测点的残差，对其进行融合. 坝体内不同部位的测点，受工作环境、仪器精度等因素的影响，其监控模型的精度也会有差异，测点残差值的规律性也各不相同. 因此，在融合时需要考虑融合权重. 对于某些测点，其残差序列的波动较大，在评价大坝整体性态时，这类测点应重点关注，即应赋予较高的权重；相反，对于残差规律性较好的测点，其权重可适当降低. 这种权重分配方式可以通过信息熵[17]理论实现，该理论用信息熵来衡量序列的不确定性，若序列的离散程度越高，波动越大，其信息熵越高. 对于第i个测点的残差序列 Δi，其信息熵EΔi的计算公式为：

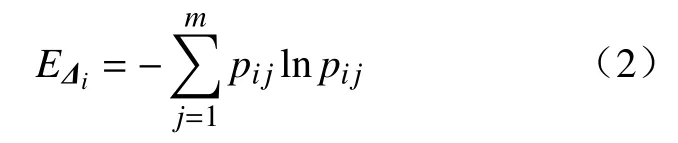
式中，pij为 Δi中第j次残差 Δij的概率值，

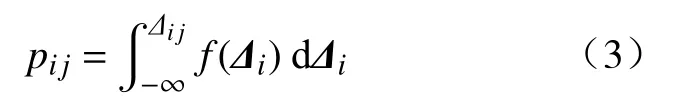
式中f(Δi)为 Δi的概率密度曲线，通常认为 Δi服从正态分布[15].

由式（2）～（3）可计算各测点残差序列的信息熵，由此计算 Δi的权重为：

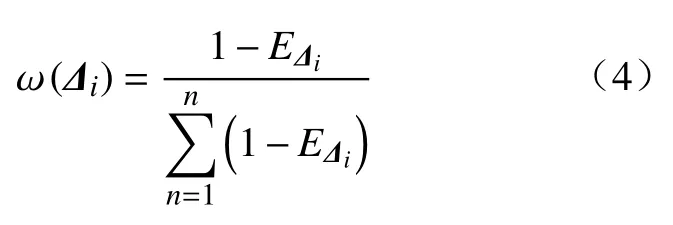
由此得到融合残差：

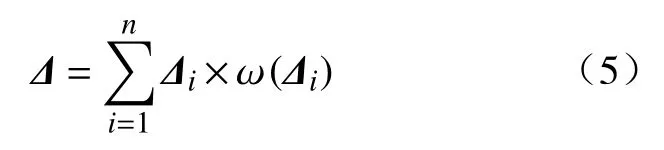
1.3 构建大坝整体性态评价模型

融合残差 Δ是表征大坝整体性态的关键指标，但由于 Δ为 [Δ1,Δ2,···,Δi,···,Δn]T的加权组合，某个 Δi异常或者 Δi中的某次残差值 Δij异常都将对 Δ产生影响，即可能会因为局部性态异常而影响到对大坝整体性态的评价. 因此在评价大坝整体性态时，评价方法应体现出模糊性，即认为大坝的整体性态对“正常”或者“异常”等定性概念均具有一定的隶属关系，利用最大隶属度原则评价大坝的整体性态.

云模型[18-19]是反映定性概念的模糊性和随机性、实现定性概念与定量数据相互转换的工具.设U是一个用精确数值表示的定量论域，C是U上的定性概念，若U内的数值x对C的隶属度μ(x)是有稳定倾向的随机数，且满足其中则x在U上的分布称为云，每一个x称为一个云滴， μ (x)应满足：

式中，Ex,En,He分别称为云的期望、熵、超熵，是用于描述云形状的数字特征. 其中，Ex是云滴在论域空间分布的中心值，是U中最能够代表定性概念的点值；En反映了云滴的离散程度；He是En的不确定性度量，反映了云滴的凝聚程度.

通常，对于某定性概念，云模型的特征参数Ex,En,He均未知，需要根据隶属于该定性概念、容量为n的数据样本 (x1,x2,···,xi,···,xn)，经逆向云发生器获取[20]，算法为：

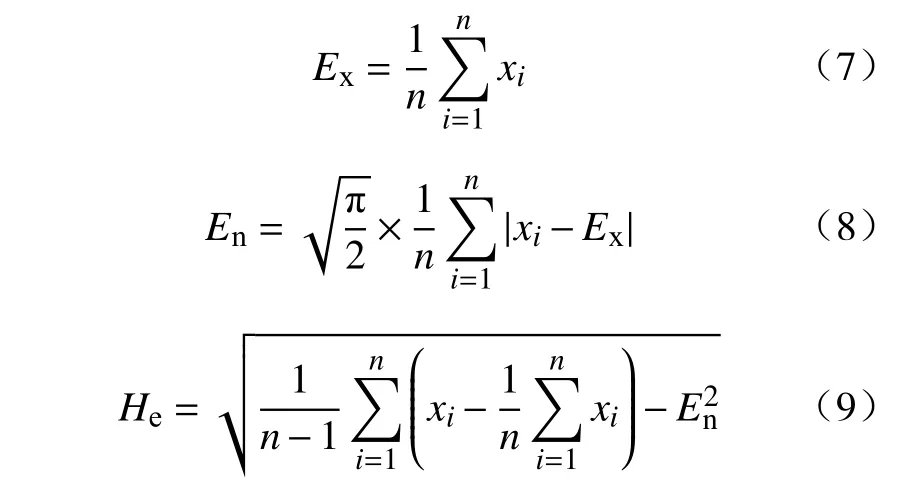
在得到云数字特征后，通过云正向发生器[21]，即可得到定性概念的云模型，计算方法为：

（1）根据云的数字特征生成以Ex为期望，En′为标准差的N个正态随机数 (t1,t2,···,ti,···,tN)；

（2）将 (t1,t2,···,ti,···,tN)代入式（6）计算隶属度，生成N个云滴.

一个定性概念的云可记为C(Ex,En,He)，其图像如图1所示.

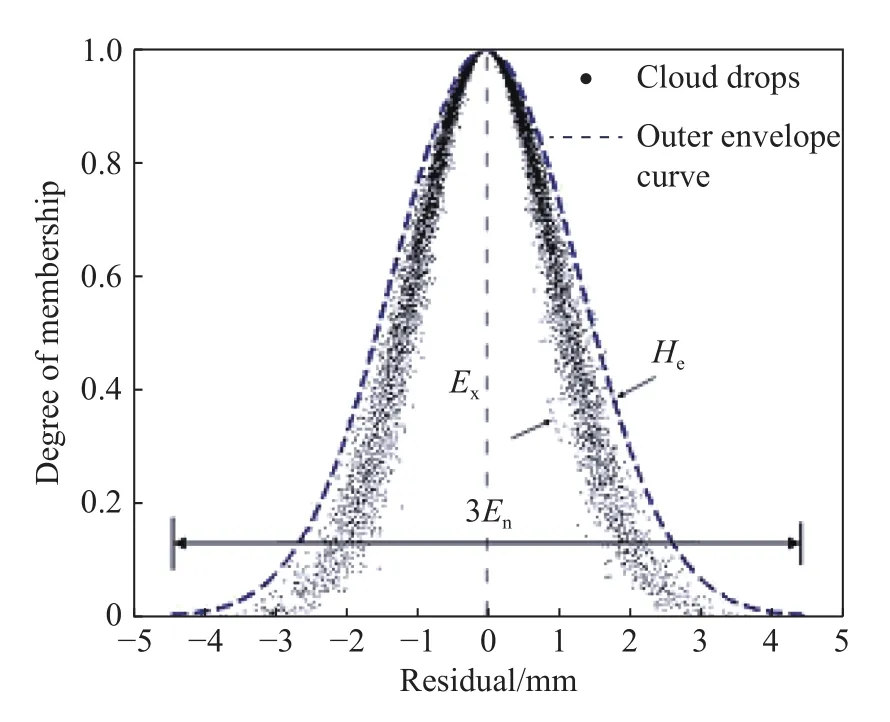
图1 云的数字特征和外包络曲线Fig.1 Characteristics and envelope curves of the cloud

图1同时绘制了描述云整体性态的外包络曲线. 外包络曲线以内包括了99.7%的云滴，用于描述云滴的分布规律及其整体结构. 云C(Ex,En,He)的外包络曲线y表达式为：

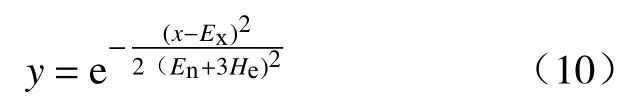
单个云模型描述了单个定性概念的模糊性和随机性，若论域中有k个定性概念，即表明存在k个云模型（分别记为Ci(Ex,i,En,i,He,i)， (i=1,2,···,k)），这些云模型构成了描述该论域所有定性概念的集合，称为概念云. 当该论域中存在其他云（记为Cq(Ex,q,En,q,He,q)时，可分别计算Cq与概念云Ci(i=1,2,···,k)的云相似度，若Cq与Cl(l∈(1,2,···,k)）云相似度最高，则认为Cq属于第l个定性概念.

目前，基于包络曲线[22-23]的云相似度计算方法在工程中得到了较为广泛的应用. 该方法的特点在于：能够在计算过程中能够同时考虑云的数字特征与形状，从而提升计算结果的可靠性. 在包络曲线法中，外包络曲线法[24]能够让云模型的3个数字特征都参与相似度计算, 进而更加精细地描述云朵之间的相似特征. 本文基于外包络曲线开展相似度计算，设Cq与云模型Cl的外包络曲线分别为yq和yl，首先计算yq和yl相交重叠部分的面积S，再求解yq和yl与坐标轴所围面积Sq、Sl，则两个云模型的云相似度 η为：

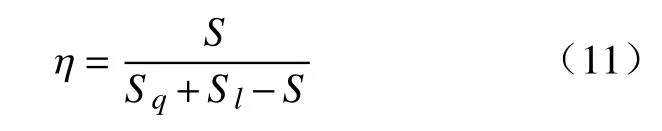
图2绘制了不同相交条件下yq和yl的重叠面积S，各相交条件下S以及Sq,Sl的计算方法见表1.

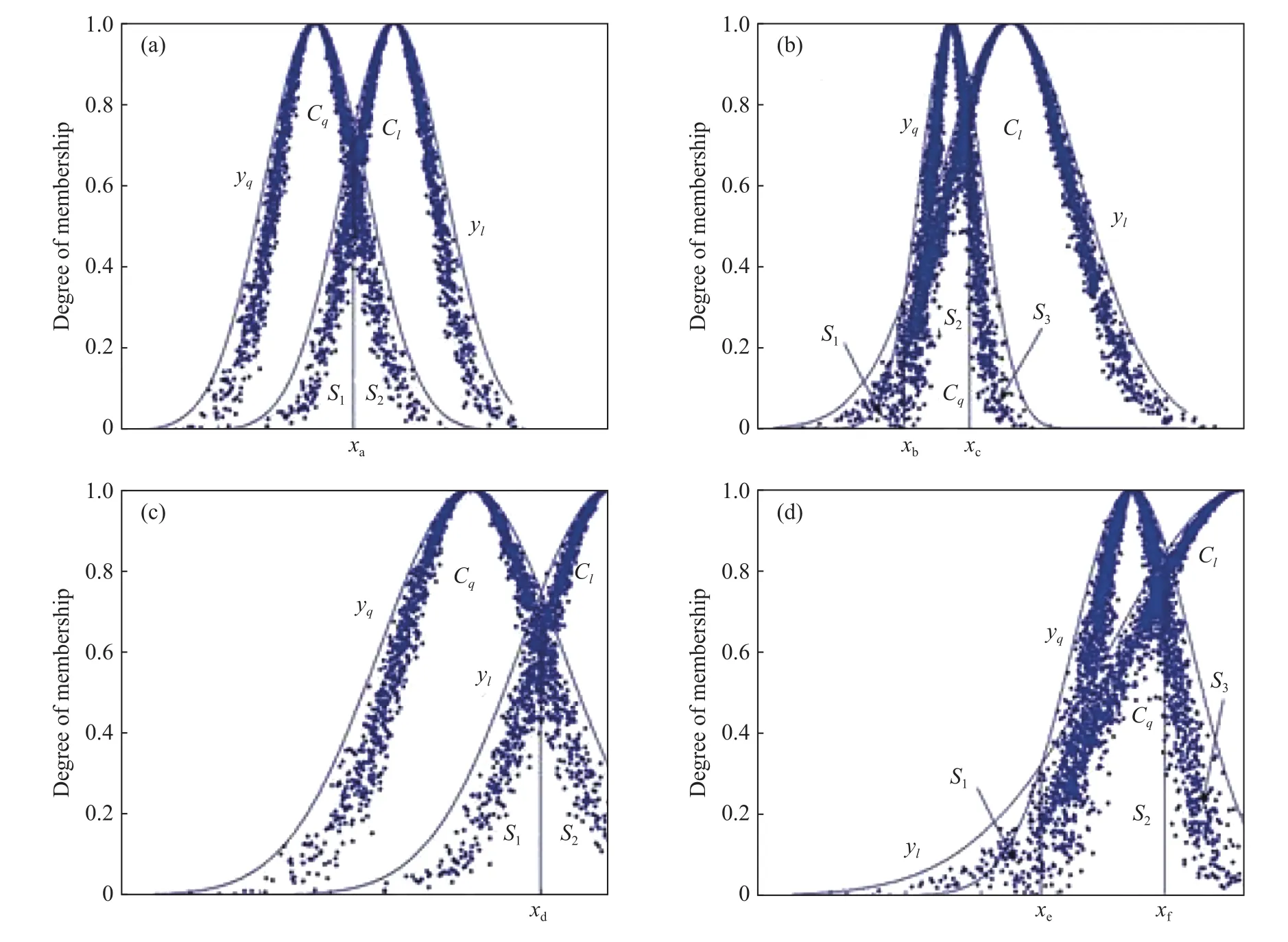
图2 不同相交条件下的云重叠面积. （a）全云 Cq与 Cl相交，一个交点；（b）全云 Cq与 Cl相交，两个交点；（c）半云 Cq与 Cl相交，一个交点；（d）半云Cq与Cl相交，两个交点Fig.2 Overlapping area of clouds under different intersection conditions: (a) entire cloud Cq intersecting Cl with one intersection; (b) entire cloud Cq intersecting Cl with two intersections; (c) half cloud Cq intersecting Cl with one intersection; (d) half cloud Cq intersecting Cl with two intersections

表1 云重叠面积计算方法Table 1 Calculation method of the cloud overlapping area

若以历史监测资料的融合残差 Δ为评价依据，将云理论应用于构建大坝整体性态的评价模型，首先需要确定 Δ的定性概念数量以及概念云. 在工程应用中，大坝性态通常被划分为“正常”、“基本正常”和“异常”3种状态[10]. 因此，本文的定性概念数量为3，最终将生成包含“正常云”、“基本正常云”和“异常云”在内的概念云，即大坝整体性态的评价标准.

概念云的生成过程，可结合 Δ的概率密度曲线f(Δ)、逆向云发生器、正向云发生器实现. 理论上，大坝各测点的测值残差近似服从正态分布[10]，Δ是测点残差的线性组合，也应近似服从正态分布，其概率密度曲线如图3所示. 经典的大坝安全监控理论[15,25]认为：若将 Δ 的标准差记为 σ ，则位于“ 2 σ”范围内的残差（约占残差总数的95.5%）属于正常残差；位于 (- 3σ,-2σ)和 [2 σ,3σ]范围内的残差（约占残差总数的4.2%）属于正常残差与异常残差的过度值，称为基本正常残差；位于 (- ∞,-3σ)和[3σ,+∞]范围内的残差（约占残差总数的0.3%）属于异常残差. 采用逆向云发生器提取各区间内残差的云特征参数，再采用正向云发生器生成概念云，则生成的评价标准将能反应各区间内残差的真实特征，有利于开展性态评价.

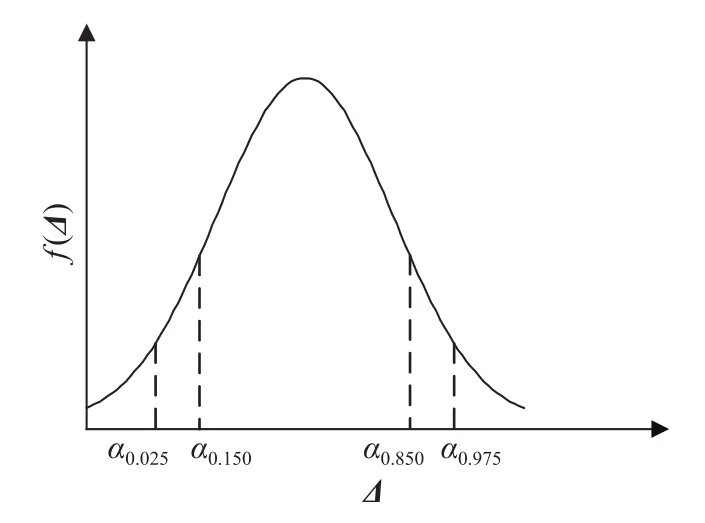
图3 Δ概率密度曲线及下分位点位置示意Fig.3 Probability density curve of Δ and the fractile

同时，需要注意到样本容量对特征参数的影响[26-27]. 在提取云特征参数的过程中，若样本容量较少，将影响参数的精度[28]. 例如，经典理论中的基本正常残差区间、异常残差区间，其包含的残差数量过少（仅为4.2%以及0.3%），由此得到的云特征参数将具有较高的随机性与离散性，进而影响概念云的可靠性. 为解决这一问题，本文对残差区间的范围进行了调整（图中 α表示下分位点，即某次残差值落入 (- ∞,μα)区间内的概率为α）：

（1）Δ中处于 [α0.150,α0.850)区域内的残差数量占总残差数量的70%，将该区间内残差定义为正常残差.

（2）Δ中处于 [α0.025,α0.150)和 [α0.850,α0.975)区间内的残差数量占总残差数量的25%，将该区间内的残差定义为基本正常残差.

（3）Δ中处于 (- ∞,α0.025)和 [α0.975,+∞)区间内的残差数量占总残差数量的5%，已达到小概率阈值[11]. 因此，将该区域内的残差定义异常残差.

分析图3可知，本文适当降低了正常残差的区间范围，并提高了基本正常、异常残差的区间占比，有利于丰富该区间内残差的样本数量，提升特征参数的可靠性；同时提升了小概率阈值，有利于工程安全.

由上述方法划分f(Δ)的区间范围后，采用式（7）～（9）逆向云发生器提取各区间内的残差特征参数，再通过正向云发生器生成对应的云模型，可得到大坝整体性态的评价标准（概念云），如表2.

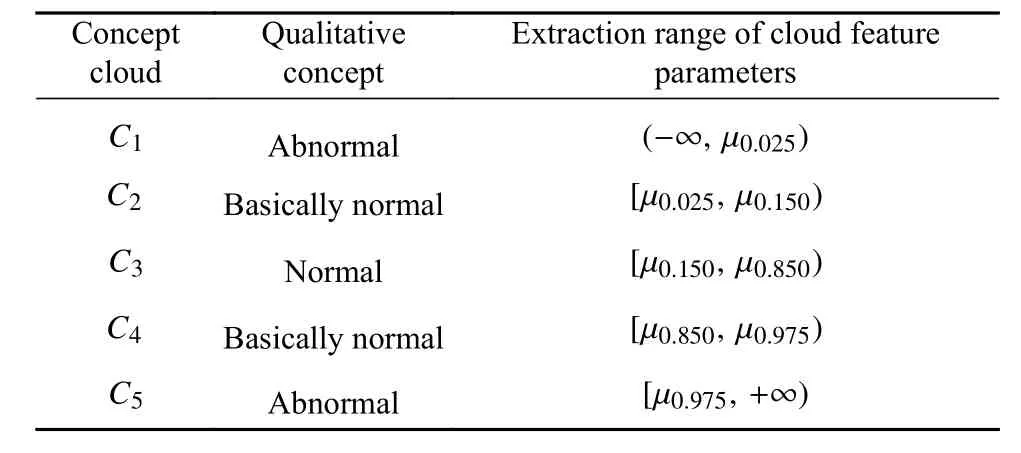
表2 大坝整体性态评价标准(概念云)Table 2 Evaluation criteria for the integrity of a dam (conceptual cloud)

在构建了表2评价标准（概念云）后，结合表1云相似度计算方法，便形成了大坝整体性态评价模型. 当需要评价某时段内的大坝整体性态时，首先计算该时段内的融合残差序列，经逆向云发生器得到该时段内的云模型特征参数后，再由正向云发生器得到该时段的评价云. 根据表1分别计算评价云与表2中C1,C2,C3,C4,C5的相似度，由最高相似度确定该时段内的大坝整体性态.

2 工程算例

万安水利枢纽位于中国江西省赣江中游万安县境内，由混凝土重力坝、土石坝和通航建筑物（船闸）组成. 枢纽设计正常蓄水位96 m，设计洪水位100 m，校核洪水位100.70 m. 其中混凝土重力坝坝顶高程104 m，最大坝高46.04 m，布置了较为完善的变形、渗流自动化监测系统. 在坝顶101.6 m高程观测廊道内布置了一条引张线(EX4)监测坝顶水平位移变化情况. 该引张线贯通整个混凝土坝，且在每个坝段均设置了一个测点，共25个，如图 4（a）所示.

本文收集了位于溢流坝段（表孔泄流）的EX401～EX409测点，从1999—2009年（共16 a）的监测数据，各测点过程线如图4（b）所示. 由图可知，各测点的变化规律相近，均表现出年周期性. 考虑到建立概念云需要长期的、丰富的学习样本，并且1999—2009年的监测资料变化平稳，有利于建模.因此，将1999—2009年作为建模期，利用该时段内的监测数据以及环境量建立监控模型（上游水位、位移等环境量如图4（c）所示），在此基础上构建评价溢流坝段（表孔泄流）整体性态的概念云.同时，考虑到评价阶段应该体现大坝性态的多年变化过程，因此，将2010—2014年作为评价期，以年为单位，评价该坝段在各年的整体性态. 为提升监控模型的预报精度以及性态评价模型的可靠性，在开展计算前，已对原始监测资料进行了前处理，删除了部分由于仪器问题导致的异常测值.

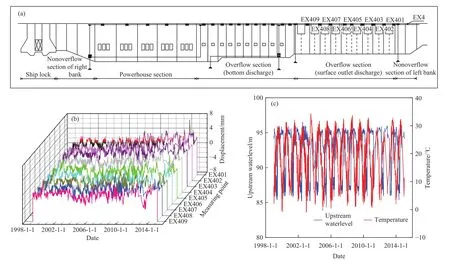
图4 混凝土坝监测信息. （a）坝顶引张线示意图；（b）EX401～EX409测点过程线；（c）上游水位与温度过程线Fig.4 Monitoring information of a concrete dam: (a) extension line in the dam crest; (b) process line of EX401-EX409; (c) process line of the upstream water level and temperature

2.1 各测点监控模型的建立

对EX401～EX409测点的原始监测数据进行前处理后，在分析时段内，各测点均存在数据缺失，且缺失时段不同. 因此有必要对各测点数据进行同步，即仅保留各测点均有测值的时段. 同步后，建模期内共3271组数据，评价期共1014组数据. 由式（1）采用逐步回归方法建立建模期内EX401～EX409各测点的监控模型，模型计算值与实测值的相关系数R如表3所示.

表3 EX401～EX409监控模型计算值与实测值相关系数Table 3 Correlation coefficient between the calculated value and measured value of EX401-EX409

由表3可知，各测点监控模型计算值与实测值的相关系数在0.802～0.895之间，总体上，各测点模型精度较高.

2.2 融合权重分析

计算建模期各测点的残差序列，并根据信息熵理论，由式（2）～（4）分析评价期内各测点残差的融合权重，如表4所示. 对比表3和表4可知，相关系数与权重有一定的程度的相关关系，但并不完全为线性相关，总体上表现为：测点的R越高，权重值越低，符合信息熵理论的概念. 当R较高时，表明该测点的模型计算值接近实测值，残差越稳定，所对应的权重就越低；当R较低时，表明该测点的模型计算值与实测值相差较大，残差波动较大，所占权重就越高.

表4 各测点残差的权重Table 4 Weight of residuals of each point

根据表4列出的权重，根据式（5）计算融合后残差 Δ的过程线如图5所示.

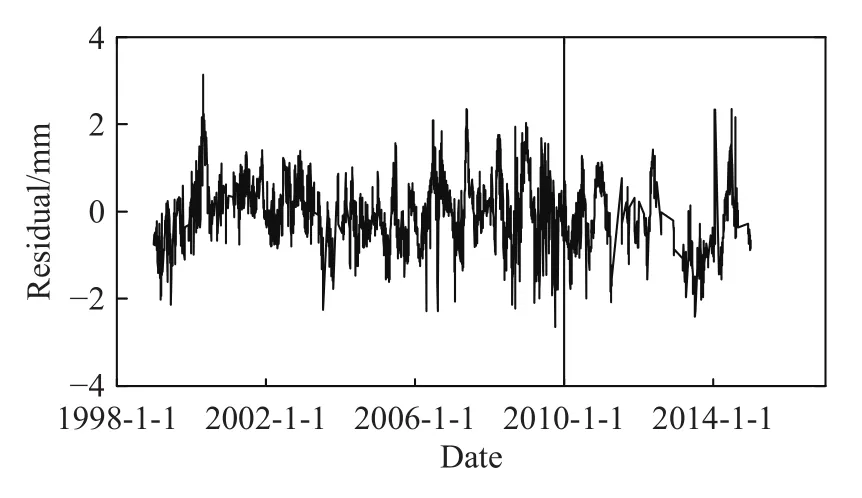
图5 融合残差过程线Fig.5 Process line of fusion residual

2.3 性态评价

经检验，Δ近似服从正态分布. 采用核密度函数估计其概率密度曲线f(Δ)，可表达为：

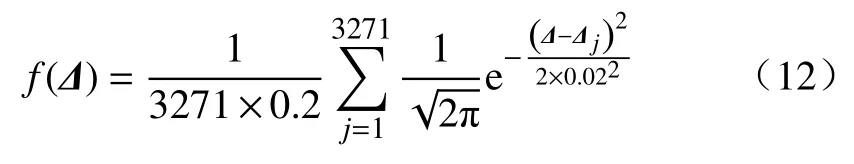
式中， Δj为 Δ内的任一残差值. 绘制该曲线，结合图3和表2，将f(Δ)划分为“正常”区间、“基本正常”区间和“异常”区间，得到f(Δ)的特征分位点如图6（a）所示. 分别统计不同区间内的残差，由式（7）～（9），采用逆向云发生器提取各区域残差的云模型特征参数，见表5. 再由正向云发生器生成大坝整体性态评价标准（概念云），包含“正常云”、“基本正常云”和“异常云”，如图 6（b）.

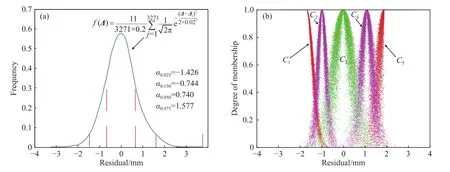
图6 融合残差特征. （a）融合残差的概率密度曲线与特征分位点；（b）大坝整体性态评价标准（概念云）Fig.6 Characteristics of fusion residuals: (a) probability density curve of fusion residuals and feature quantiles; (b) evaluation criteria for the integrity of a dam (conceptual cloud)

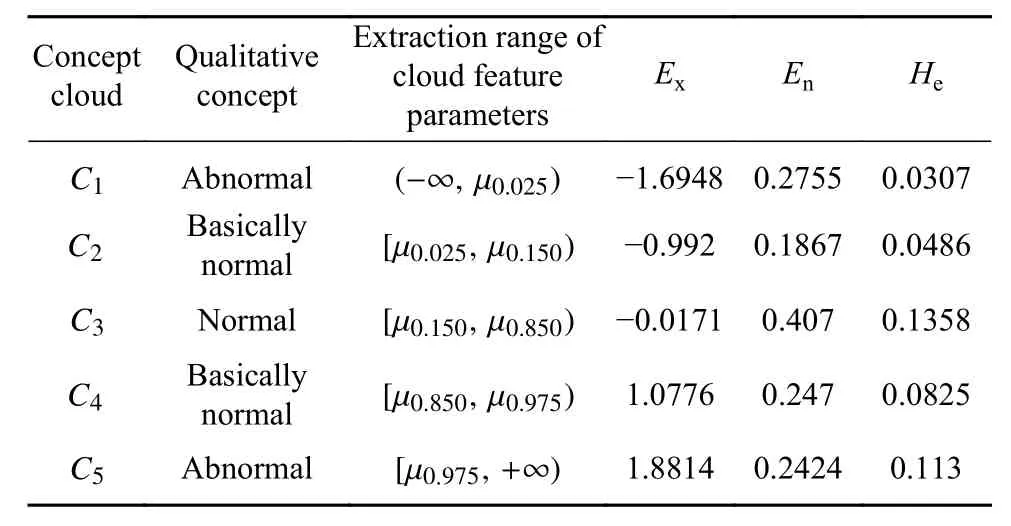
表5 概念云特征参数Table 5 Characteristic parameters of the concept cloud

基于概念云，可对评价期内的大坝整体性态进行评价. 以年为单位，由逆向云发生器逐年计算2010年至2014年融合残差的云特征参数，如表6，再由正向云发生器可得到各年的评价云. 将概念云C1,C2,C3,C4,C5的外包络曲线分别记为y1,y2,y3,y4,y5；2010年至2014年评价云的外包络曲线分别记为y2010,y2011,y2012,y2013,y2014，由式（10）计算后，如图 7 所示.

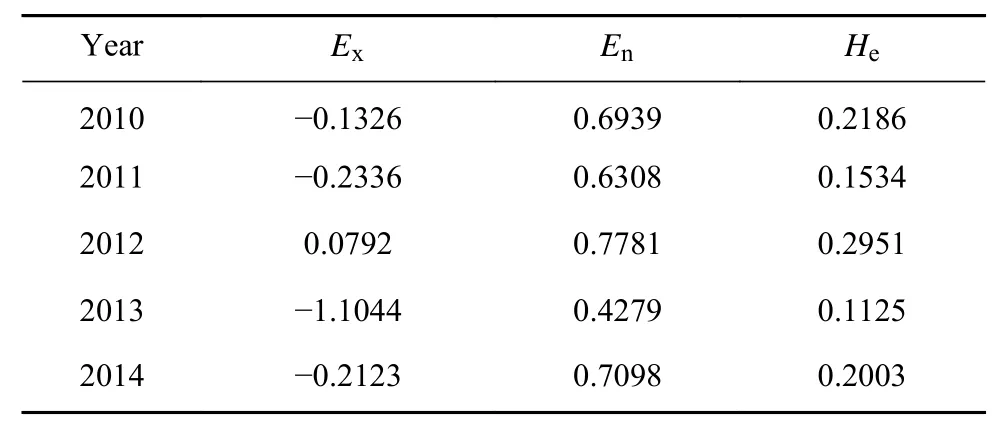
表6 2010—2014年各年度云特征参数Table 6 Cloud parameters for each year from 2010—2014

将同一年份的评价云与概念云C1,C2,C3,C4,C5的 相 似 度 分 别 记 为 η1,η2,η3,η4,η5， 根 据表1可计算2010—2014年，各年评价云与概念云的相似度，见表7.

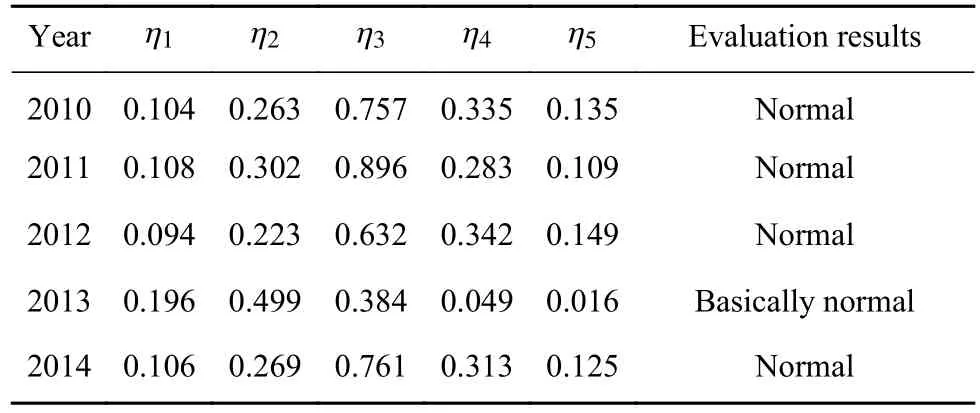
表7 2010—2014年各年评价云与概念云的相似度Table 7 Similarity between evaluating clouds and concept clouds from 2010 to 2014

由表7可知，各年的评价云与C1,C2,C3,C4,C5均有一定的相似度. 其中，与C1,C5的相似度很低，仅在0.1附近波动. 这表明在各年的融合残差中，虽然存在少量的异常残差，但总体上，评价云的形态仍然与C1,C5存在较大差异，因此没有影响到对大坝整体性态的评价. 产生这些异常残差的原因可能包括：1）采用逐步回归算法得到的监控模型是一种线性模型，当大坝处于某些特殊工况（例如：高水位工况）下运行时，大坝处于非线性变形状态，采用线性模型得到的模型计算值不准确，导致残差较大；2）部分测点（局部性态）出现了性态异常.

除2013年外，其他年份的评价云与C3的相似度最高，在0.7附近波动，表明溢流坝段（表孔泄流）在这些年份中，整体性态正常. 对于2013年的评价云，与C2的相似度最高，主要原因在于该年份缺测次数较多（缺测217次），导致样本点偏少，由此生成的评价云不能较好的描述该年份内残差的整体特征. 总体上，该年度的评价云在形态上更加接近C2，未达到异常水平，因此溢流坝段（表孔泄流）整体性态“基本正常”.

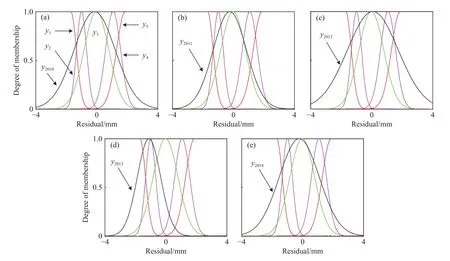
图7 概念云与评价云 (2010—2014 年)外包络曲线. （a）2010 年；（b）2011 年；（c）2012 年；（d）2013 年；（e）2014 年Fig.7 Concept cloud and evaluation cloud envelope curve during year of 2010—2014: (a) 2010; (b) 2011; (c) 2012; (d) 2013; (e) 2014

3 结论

（1）信息熵能够反映测点残差的波动情况，将信息熵的这一特征用于多测点残差融合权重的分析，有利于识别残差不稳定的测点，对其赋予较高的权重，进而为提升性态评价结果的可靠性提供必要条件. 在工程应用中，可在此基础上，结合监测部位的重要程度等多因素进一步优化权重分配方法.

（2）本文提出的概念云建立方法，能够有效提取残差在不同性态区间内的特征信息，进而能够建立有效的大坝整体性态评价标准. 在工程应用中，对于“正常残差”、“基本正常残差”、“异常残差”的概率区间范围，可结合实际情况，进行适当调整.

（3）将云理论用于大坝整体性态的评价，通过计算各年的评价云与概念云的相似度，最终由最大相似度确定大坝整体性态，体现了评价过程的模糊性，评价过程客观、定量. 算例表明，受建模算法、局部异常等因素的影响，各年中均有少量异常残差，这些少量的异常残差会在评价过程中有所体现，但不会影响对大坝整体性态的评价结果，因此评价模型能够兼顾局部与整体之间的关系，评价结果合理、可靠.