湍流中气泡破碎建模与实验研究进展

张华海，王悦琳，李邦昊，王铁峰

（清华大学化学工程系，北京 100084）

引 言

气-液和气-液-固多相流广泛存在于石油化工、矿物浮选、食品加工、废水处理、生物制药等领域[1-8]。气泡聚并和破碎行为通常决定了分散相在连续相流场内的尺寸分布和分散状况，因而对体系的传热、传质及反应性能有着重要影响[9-10]。气泡在连续相液体中的分散存在于许多工业过程中，如化学、石油、制药和食品工业。气泡尺寸分布是破碎和聚并平衡的结果[11-12]，是气液相界面积和动量、质量、热量传递速率的关键参数[13-16]。由Hulburt等[17]提出的群体平衡模型(PBM)可以用来预测气泡的尺寸分布。气液体系中气泡的PBM方程可以表示为[18-19]：

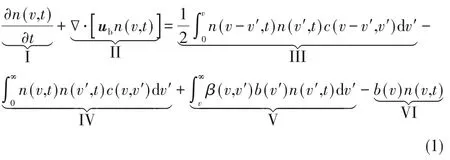
其中，Ⅰ～Ⅵ分别代表时间项、对流项、聚并引起的源项、聚并引起的汇项、破碎引起的源项、破碎引起的汇项。为了求解式(1)，需要给定气泡破碎速率b(v)、气泡聚并速率c(v)和子气泡尺寸分布β(v)。

因此，正确建立气泡破碎模型，从而准确预测气泡破碎速率和子气泡大小分布，对可靠地模拟气液多相流体系非常重要。完整的气泡破碎模型包括气泡破碎速率和子气泡尺寸分布。在这方面已经有大量的文献报道，本文主要综述气泡破碎模型的发展情况，并对其进行深入讨论，以更好地理解气泡破碎机理和建模。

对气泡破碎模型进行验证，需要准确可靠的实验数据。气泡变形破碎过程复杂，且破碎时间通常为毫秒尺度，准确清晰地捕捉气泡破碎信息变得尤为重要。高速摄像技术的快速发展，实现了对毫秒级变化进行高清且快速的捕捉，促进了气泡破碎实验的研究。气泡破碎实验的关键还在于创造气泡破碎条件，包括单气泡的释放和湍流产生方式的设计。本文综述了文献中不同类型的气泡破碎实验，对其优缺点进行分析，为气泡破碎实验设计和数据收集提供指导。

1 气泡破碎模型

连续相液体性质、体系压力和温度等操作条件、气液相互作用和输运现象对气泡在湍流中的破碎有着显著影响。一般来说，破碎机制可以归结为连续相的气泡外部应力和气泡表面张力之间的相互作用。文献结果[20-21]表明，气泡破碎主要有四种机制，分别是湍流涡碰撞、黏性剪切、尾涡剪切脱落和界面不稳定性（图1）。在充分湍流中，湍流涡碰撞机理往往占主导地位，因此针对该破碎机理的气泡破碎模型最多。

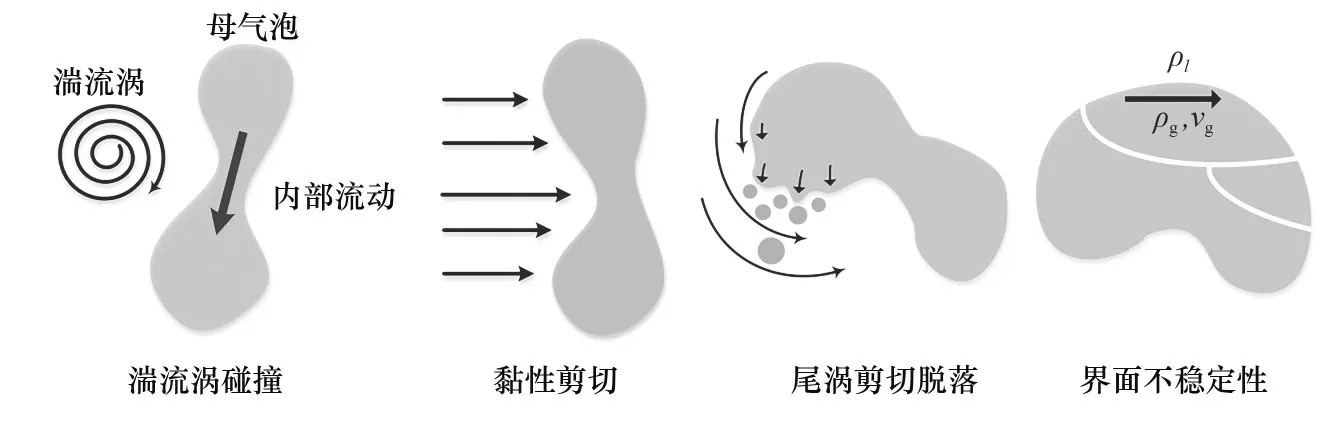
图1 气泡破碎机理示意图Fig.1 Schematic of bubble breakup mechanisms

1.1 湍流涡碰撞引起的气泡破碎

在充分湍流中，气泡破碎主要是由湍流涡碰撞引起的。当湍流涡碰撞带来的动态压力增大时，气泡变形并且颈部不断收缩，在满足一定条件下，最终破碎成两个或两个以上的子气泡。从气泡表面压力平衡的角度，气泡破碎机制可以描述为外部破裂应力与维持气泡形状的界面内聚应力之间的平衡。

近30年来，科研者通过增加气泡破碎新准则、考虑多子气泡破碎机制、拓展湍流能谱、考虑气泡形状变化和气泡内部流动等，不断地发展和完善湍流涡碰撞机制下的气泡破碎模型。因此，气泡破碎模型能够较好地预测不同压力、温度、液体黏度、表面张力等复杂条件下的气泡破碎速率和子气泡尺寸分布。

根据压力约束或能量约束的不同破碎准则，文献报道的气泡破碎模型至少可分为以下六类：

(1)具有小于母气泡直径尺寸湍流涡的与速度波动有关的湍流动能大于临界值[22-23]；

(2)气泡表面周围的湍流速度波动大于某一临界值[24-25]；

(3)湍流涡碰撞的湍动能大于某一临界值[26-29]；

(4)碰撞母气泡湍流涡的湍流惯性力大于最小子气泡表面的界面张力[12,30]；

(5)由周围连续流体产生的湍流应力大于母气泡表面恢复压力[31-32]；

(6)结合标准(3)和(4)[11,33-43]。

上述工作的研究者们对标准(3)和(5)中毛细管压力约束的临界值有着不同的定义，例如σ/d1[11,30]、2σ/d1[12]、2σ/db[35]、6σ/d1[36]、6σ/db[32]和6σ/d1-6σ/db[37]。其中，d1为气泡破碎后最小子气泡直径，db为母气泡直径。此外，能量约束的临界值在文献中也有所不同，如母气泡的表面能、破碎前后表面能的增加等。表1汇总了不同的气泡破碎判据，可以发现，气泡破碎判据不同，所得到的气泡破碎速率和子气泡分布情况存在显著差异。综合来看，在各种判据中，同时考虑压力约束判据和能量约束判据更为合理。

表1 气泡破碎判据及模型预测结果Table1 Criteria bubble breakup and model predictions

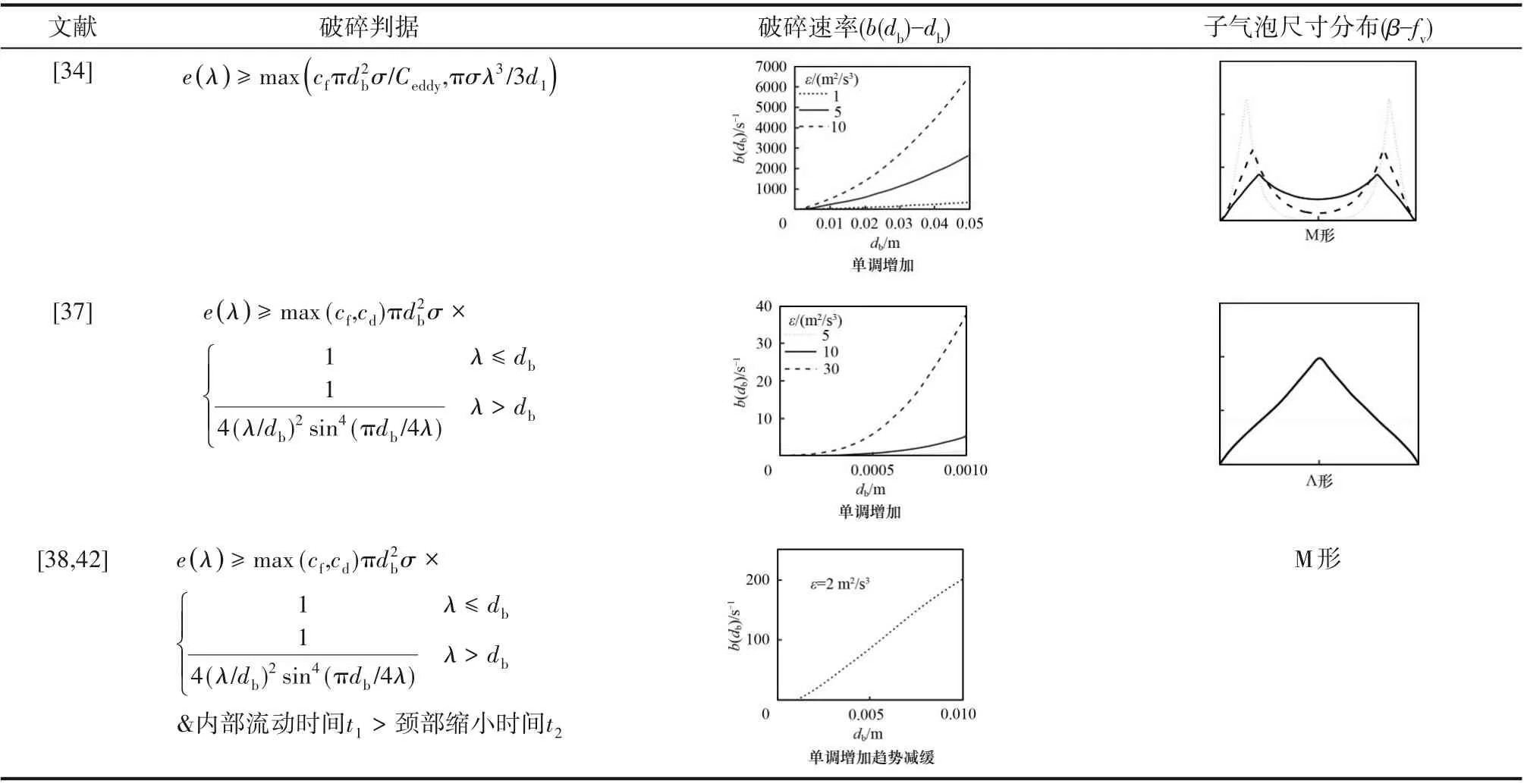
续表1

在近五年来建立的气泡破碎模型中，一些研究者考虑了多重气泡破碎[33,39,45]。在多重气泡破碎中，将气泡破碎过程视为连续过程，提出了新的破碎约束和破碎模型。图2为双气泡破碎到多重气泡破碎示意图，可以发现多重气泡破碎即连续双气泡破碎：母气泡分裂成一个最大的子气泡和一个最小的子气泡，进而，最大的子气泡又分裂成另一个较大和更小的子气泡，直到最后一次分裂产生的较大的子气泡继续分裂[图2(d)]。

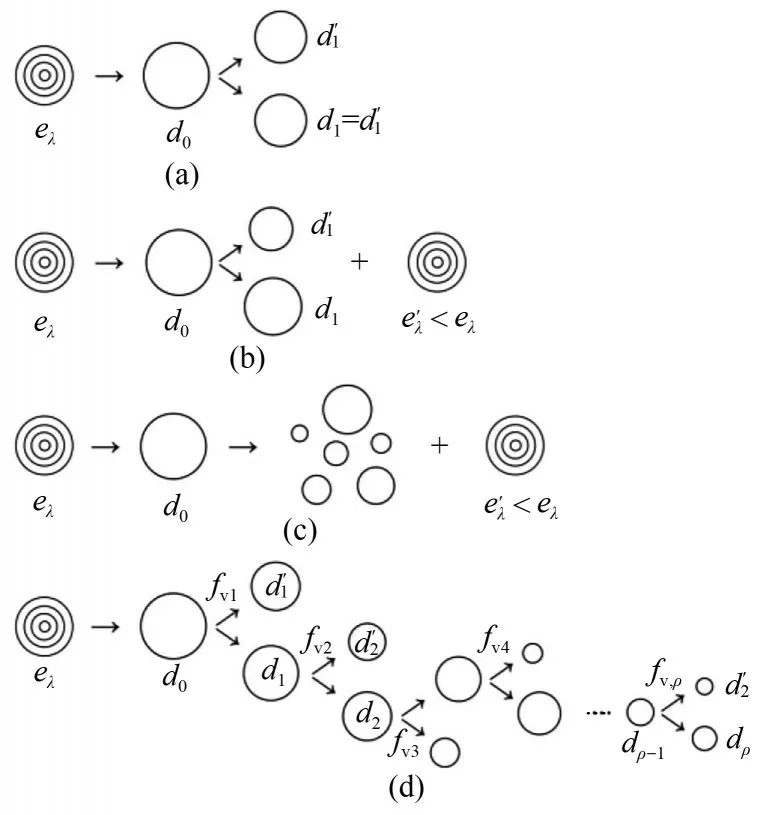
图2 气泡与湍流涡碰撞破碎的不同情况[33]：(a)等大小双气泡破碎；(b)非等大小双气泡破碎；(c)直接多气泡破碎；(d)连续二元破碎导致多重子气泡Fig.2 Different cases for breakup of fluid particle colliding with a turbulent eddy[33]：(a)binary equal-sized breakup;(b)binary unequal-sized breakup;(c)multiple particle breakup with unused eddy energy;(d)successive binary breakup events resulting in multiple daughter particles

气泡在湍流涡的撞击下形成一个哑铃型的状态，即一个大气泡部分和一个小气泡部分，中间通过一个颈部连接。在实验中，发现了气泡破碎过程中的内部流动现象，即气体可以从母气泡变形过程中产生的小气泡部分通过变形气泡的颈部流向大气泡部分[46-47]，如图3所示。Xing等[38]将一个重要的现象包含到气泡破碎模型建立过程中，从而提出了内部流动破碎模型，并且成功预测了压力对破碎速率的影响规律。

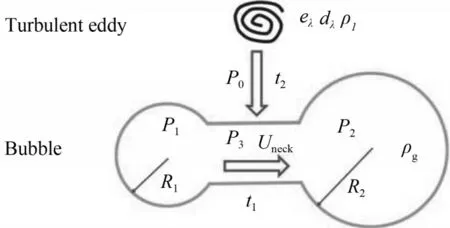
图3 气泡破碎机理示意图[38]Fig.3 Sketch of the dynamic process of a bubble breakup[38]

以前的气泡-湍流涡碰撞破碎模型是根据只包含惯性子域的湍流能谱推导出来的。但是，在高液体黏度条件下，各向同性湍流的Kolmogorov惯性子域会减小甚至消失，如图4所示，因此仅考虑惯性子域的气泡破碎模型不再适用[48]。最近的模型[41,45,48-50]将能量谱扩展到湍流全能谱，包括耗散子域、惯性子域和含能子域，积分尺寸从Kolmogorov长度尺度扩展到湍流涡全尺度。

图4 液体黏度对湍流能谱的影响Fig.4 Effect of liquid viscosity on turbulent energy spectrum

Das[40]通过详细考虑湍流涡相对速度的方向，以及湍流涡与母气泡碰撞的角度，建立了复杂的气泡破裂模型。然而，该模型过于复杂，并不适用于PBM方程的求解。在以前的模型中，气泡形状被简化为球形，而较大气泡实际为椭球或球帽形。Shi等[43]提出了一种考虑气泡形状变化的改进破碎模型，该模型通过考虑不同尺寸气泡的不同形状，使破碎过程中表面能增加量的计算更加准确，计算的气泡破碎速率也更加合理。

表2总结了文献中典型的气泡破碎模型，包括破碎速率和子气泡大小分布。目前公认的破碎速率模型大多类比气体动力学理论计算气泡与湍流涡的碰撞频率，再由碰撞频率和破碎概率相乘得到气泡破碎速率。尽管气泡破碎模型已经得到了不断改进，能够比较可靠地预测不同条件下的气泡破碎速率和子气泡尺寸分布，但用于高压或高黏度体系仍有局限性。图5总结了湍流涡碰撞机理下气泡破碎模型的发展历程。

表2 基于湍流涡碰撞机理的气泡破碎模型Table2 Phenomenal models of bubble breakup due to turbulent eddy collision

续表2

续表2

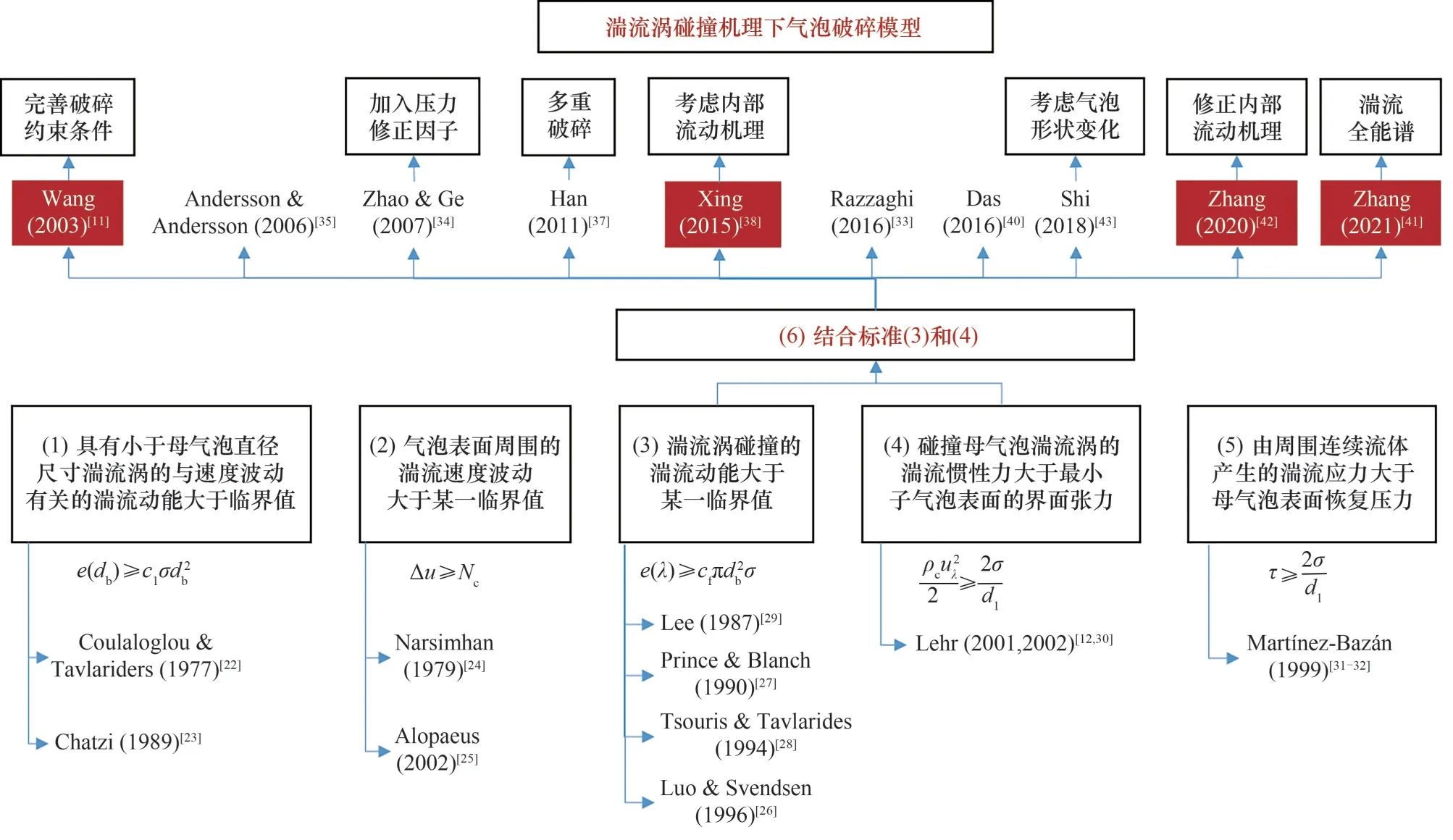
图5 湍流涡碰撞机理下气泡破碎模型发展历程（其中红色底纹的为本课题工作）Fig.5 Development history of bubble breakup model for turbulent eddy collision mechanism

1.2 黏性剪切引起的气泡破碎

在层流中，黏性剪切应力τv与表面张力应力τs的相对大小决定了气泡是否破碎。当毛细管数Ca=τv/τs或气泡尺寸超过临界值时，表面张力应力不足以保持气泡的形式，连续相的剪切应力会在气液界面附近引起速度梯度，使气泡变形并最终导致破碎。在湍流中，由于尾流效应，剪切应力也存在并产生重要影响。当一个尾部气泡在尾迹区域外有较大的部分，它将被剪切应力劈开，穿过之前的气泡尾迹边界，并导致拉伸、表面压痕和颈缩。在颈部出现掐断现象后，气泡最终分裂成两个或两个以上的子气泡[51-53]。

1.3 尾涡剪切脱落引起的气泡破碎

随着母气泡尺寸的增大，气泡形状会变得更加不规则，呈现为活塞形或球帽形气泡，气泡破碎机制也会变得更加复杂。此外，由于界面间的速度差异，剪切和界面不稳定性等机制也会存在。剪切过程的特征是大量的小气泡从一个大的母气泡中剪切出来，也被称为侵蚀破碎[20-21]。在高黏度体系中，剪切是由黏性剪切应力与活塞/球帽形气泡边缘表面应力之间的相互作用引起的。当相对速度达到某一临界值时，气泡裙面变得不稳定，从母气泡处滑移，在边缘处产生大量的小子气泡。而在低黏度体系中，界面黏性剪切应力的影响可以忽略。在这种情况下，当气体在界面附近的边界速度等于母气泡周围的环形液膜流速时，就会发生剪切过程。边界上的气体会渗透到液膜中并产生小子气泡[54-55]。根据Fu等[54]的研究，剪切气泡的体积可以表示为VSO∝πDcδeffvr，其中δeff为环形有效厚度，vr为气体流速。剪切后的气泡尺寸满足关系式ds=ξSOds,max，其中ξSO是子气泡平均尺寸与最大尺寸的比值，计算公式如下:

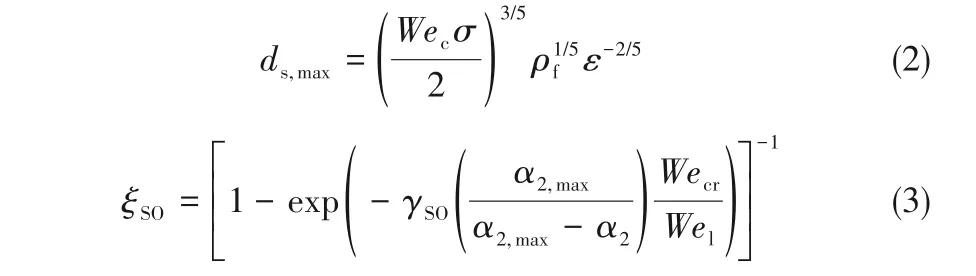
1.4 界面不稳定性引起的气泡破碎

液体中上升的大气泡，由于Rayleigh-Taylor和Kelvin-Helmholtz不稳定也会导致气泡破碎，这种破碎与分散相和连续相的密度比有关。当密度比较大时，轻流体被加速进入重流体，从而导致Rayleigh-Taylor不稳定性。当密度比较小时，Kelvin-Helmholtz不稳定性将是主要的破碎机理。Letzel等[56]根据Kelvin-Helmholtz不稳定性阐述了气体密度增加导致气泡破碎更快的结论。他们认为较高的气体密度增加了不稳定表面波的生长因子，因此大气泡的表面在更大范围的波动中变得不稳定，从而使大气泡破碎成较小的气泡。

Sun等[57]研究了球帽形气泡的界面面积输运方程，在闭合源项中考虑了湍流与气泡群之间的碰撞和大气泡尾涡相互作用引起的表面不稳定的破碎机理。界面面积密度的源项为:

Wang等[18,58-59]通过以下方法估算了大气泡截面不稳定引起的气泡破碎速率：

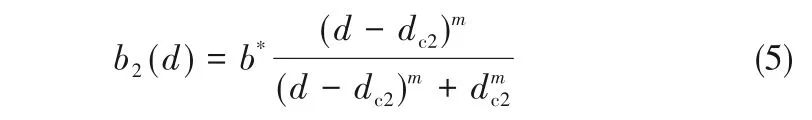
在充分湍流中，湍流涡碰撞机理占据主导地位，文献中也存在较多的气泡破碎理论模型。但是尚需建立计算过程更加简便的、能够对操作条件和物理性质变化具有普适性的气泡破碎模型。大气泡在湍流中形变较为复杂，且破碎机制尚未完全清晰。其次，颗粒或者表面活性剂对气泡破碎的影响也未得到完整的建模分析。

2 气泡破碎实验

在完全发展的湍流中，主导机制是湍流涡碰撞引起的破碎。因此，文献中关于气泡破碎的实验大多是通过制造湍流使气泡破碎来进行研究。根据湍流产生方式，如图6所示，文献报道的气泡破碎实验可分为以下几类：

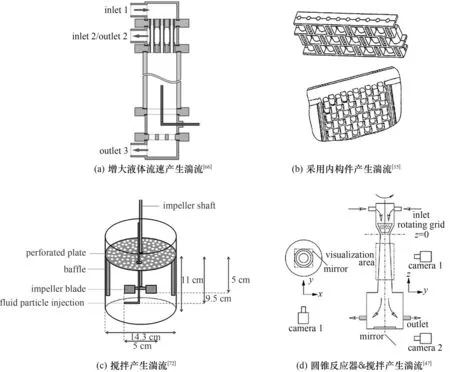
图6 气泡破碎实验装置图Fig.6 Schematic diagram of experimental set-up for bubble breakup

(1)增大液体流速产生湍流[31-32,60-69]；

(2)采用内构件产生湍流[35,46]；

(3)搅拌产生湍流[70-72]；

(4)圆锥反应器＆搅拌产生湍流[47,73]。

虽然关于气泡破碎的实验研究有很多报道，但大多是定性的，主要集中在气泡破碎现象和破碎机理上。关于气泡破碎时间、破碎概率、子气泡尺寸分布，特别是破碎速率的实验数据非常有限。此外，操作条件和气体、液体性质对气泡破碎的定量影响也鲜有报道。因此，对气泡破碎的定量实验研究还需要加强。表3汇总了目前文献中气泡破碎实验的相关情况。

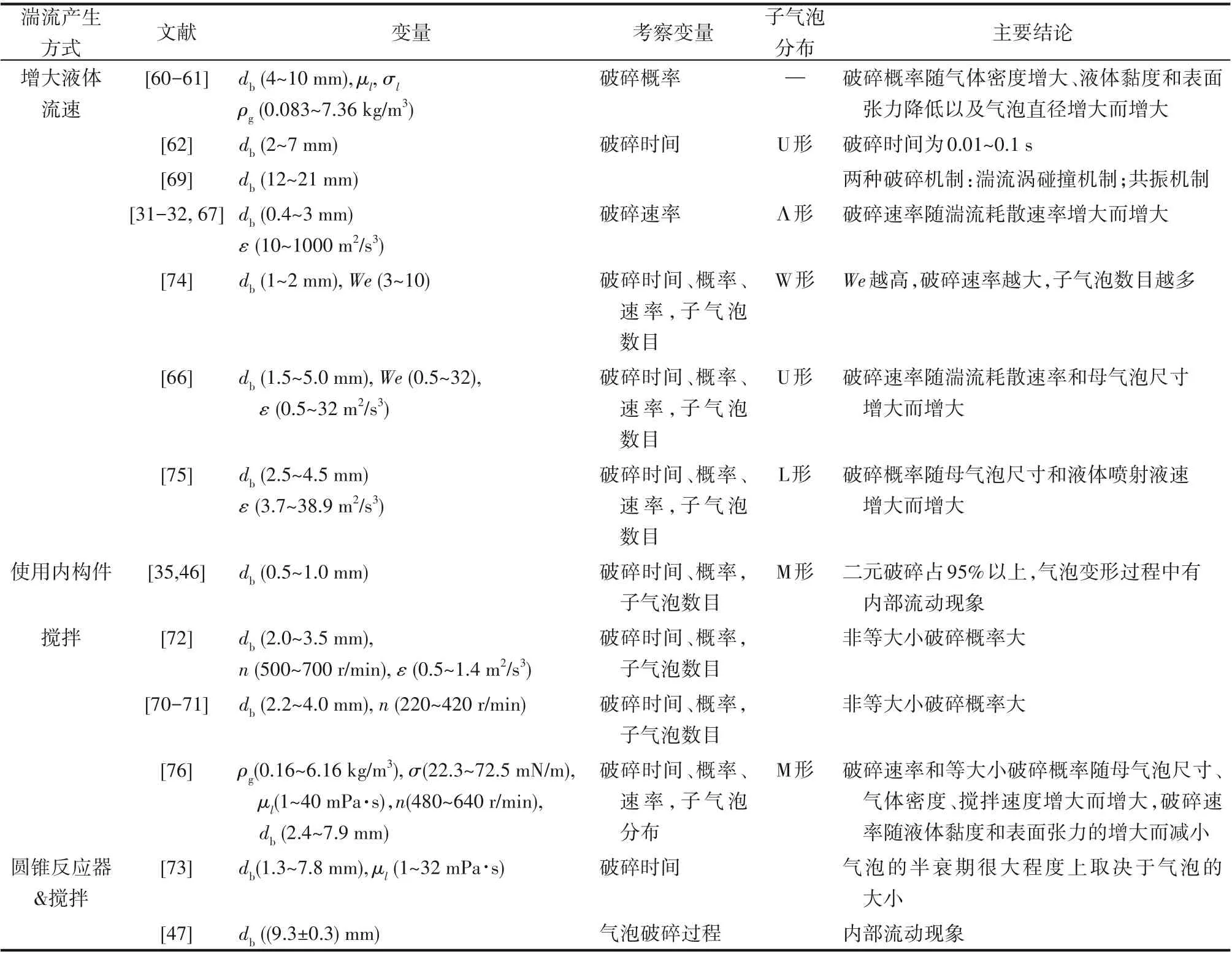
表3 文献中气泡破碎实验汇总Table3 Summary of bubble breakup experiments in the literature

实验中使用的气泡破碎速率的定义大多数基于Coulaloglou等[22]在1977年提出的公式，由气泡破碎时间tb的倒数和气泡破碎概率P(db)的乘积进行计算：

2.1 增大液体流速产生湍流

为产生足够强的液体湍流，可通过增加文丘里管道[60-62]或均质器[63-65]狭窄间隙内的液体速度，或者采用浸入式喷嘴产生高速射流[31-32,66-69,75]。这种方式产生的湍流较为均匀，但液体流速很大，产生的湍流强度相对较低。由于液体流速高，气泡变形图像非常模糊，增加了识别和分析难度。

Wilkinson等[60-61]在湍流管中观察气泡破碎过程。装置主体是一个有机玻璃文丘里管，通过较高的液体流速（2.6m/s）产生湍流，使装置下部鼓入的气泡（db=4～10mm）发生破碎，用高速相机（4000帧/s）对气泡进行观测。实验记录了超过150个气泡从注入至流到指定位置处发生破碎的个数，并得出气泡破碎概率，同时考察了不同气体密度（ρg=0.083 ～7.36 kg/m3）、液体黏度和表面张力的影响。统计结果如图7所示，直径较大的气泡破碎概率也较大，气泡破碎概率随气体密度升高而增大，且气体密度对大气泡破碎概率影响更大。另外，实验发现液体黏度和表面张力增加都会导致气泡破碎概率降低。

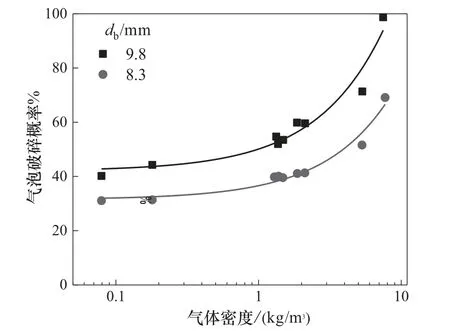
图7 湍流管流中两种不同直径气泡破碎百分比与气体密度的关系[61]Fig.7 Bubble break-up percentage versus gas density for two different bubble diameters in a turbulent pipe flow[61]

Hesketh等[62]观察了气泡和液滴在湍流管中的破碎过程，实验参数如下：气泡直径2～7mm，液体流速3.9 8m/s，相机拍摄速度1200帧/s。观察结果显示，气泡/液滴的破碎时间在0.01 ～0.1 s之间，气泡破碎后子气泡大小分布呈现U形[图8(a)]。与以上结果不同的是，Martínez-Bazán等[31]测得了Λ形子气泡分布，如图8(b)所示。在该实验过程中，底部喷嘴喷出射流液体产生充分发展的湍流，注射针将气泡持续不断地释放到中心轴处湍流区域发生破碎。他们利用数字图像处理技术测量了气泡被湍流撞击破碎产生的子气泡大小分布的演变。实验参数如下：气泡直径0.4 ～3mm，喷嘴收缩比为250∶1，液体流速8.25 ～30m/s。

图8 二元破碎子气泡分布Fig.8 Daughter bubble size distributions for binary bubble breakup

Vejražka等[66]对射流场中的气泡破碎进行了实验研究。在该实验中，水从喷嘴阵列中喷出，产生强烈湍流，向下冲击矩形玻璃室单元中向上浮起来的气泡而导致气泡破碎。实验参数如下：气泡直径1.5 ～5.0mm，液体流速0.164 ～0.20 6m/s，拍摄速度2000帧/s。利用PIV测量速度场，利用大涡PIV技术估计局部湍能耗散率。实验获得了完整的破碎频率、子气泡数目和子气泡大小分布结果。气泡破碎时间定义为从气泡进入拍摄区域内到气泡发生破碎为止，利用式(6)计算气泡破碎速率。结果如图9所示，气泡破碎速率随湍流耗散速率或者母气泡尺寸增大而增大[图9（a）中Ref.[47]为文献[66]中文献号]。另外，子气泡数目随着We（We=2ρε2/3db5/3/σ）增大而增大。实验结果统计表明，二元破碎对应的子气泡尺寸分布为U形分布。

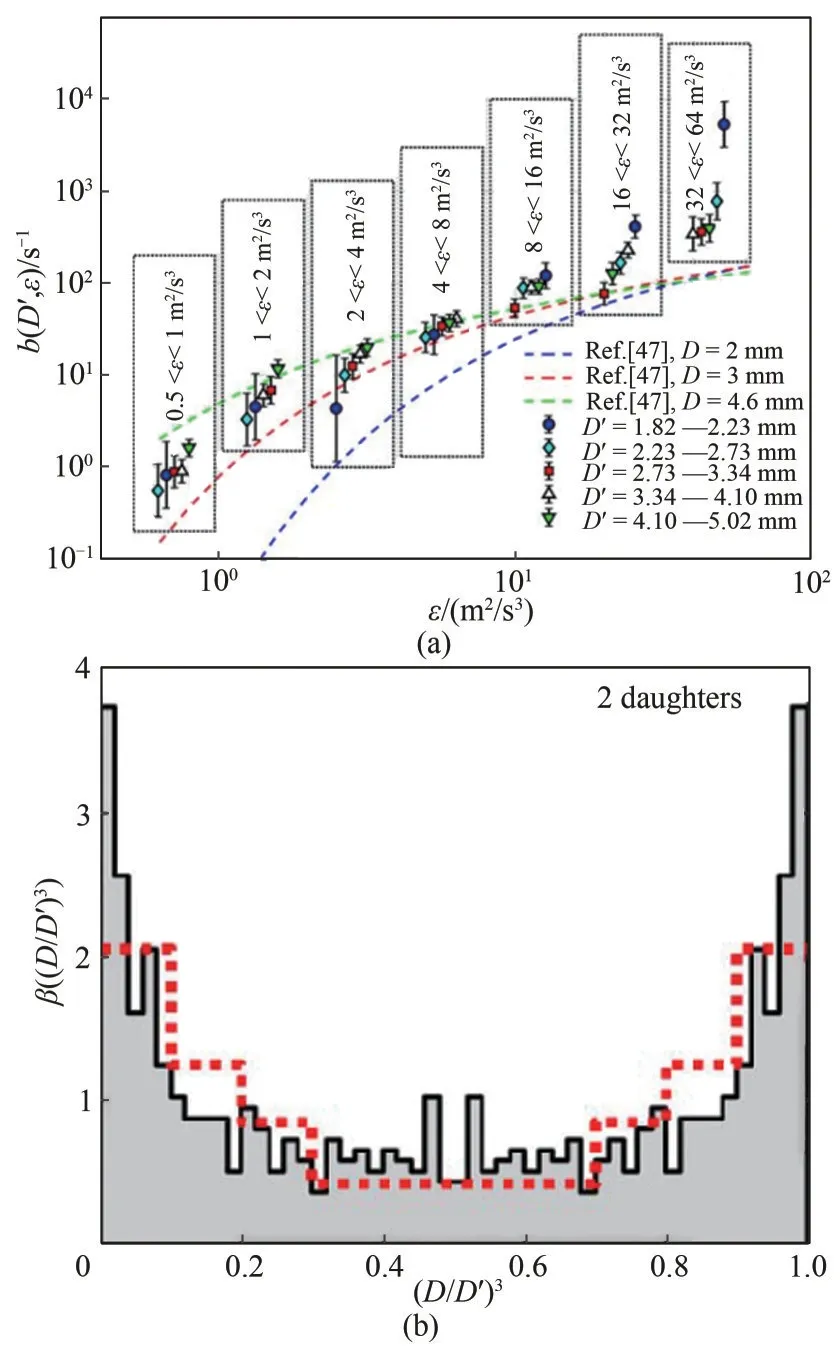
图9 气泡破碎速率和二元破碎子气泡分布[66]Fig.9 Breakage frequency and daughter bubble size distribution of binary bubble breakup[66]

类似于Vejražka等[66]的工作，Shuai等[75]对更高喷射液速射流场中的气泡破碎进行了详细的实验研究。实验参数如下：气泡直径2.5 ～4.5mm，液体流速1.42 ～4.2 6m/s，拍摄速度250帧/s。该实验完整地测量了气泡破碎时间、破碎概率、破碎速率和子气泡分布。实验结果同样发现破碎速率随母气泡尺寸和湍流耗散速率增大而增大。但是，该实验在测量子气泡尺寸分布时统计了全部多重子气泡破碎，最终得到了“L形”子气泡尺寸分布结果，如图10所示[图10（b）中Eq.[16]为文献[75]中的公式号]。

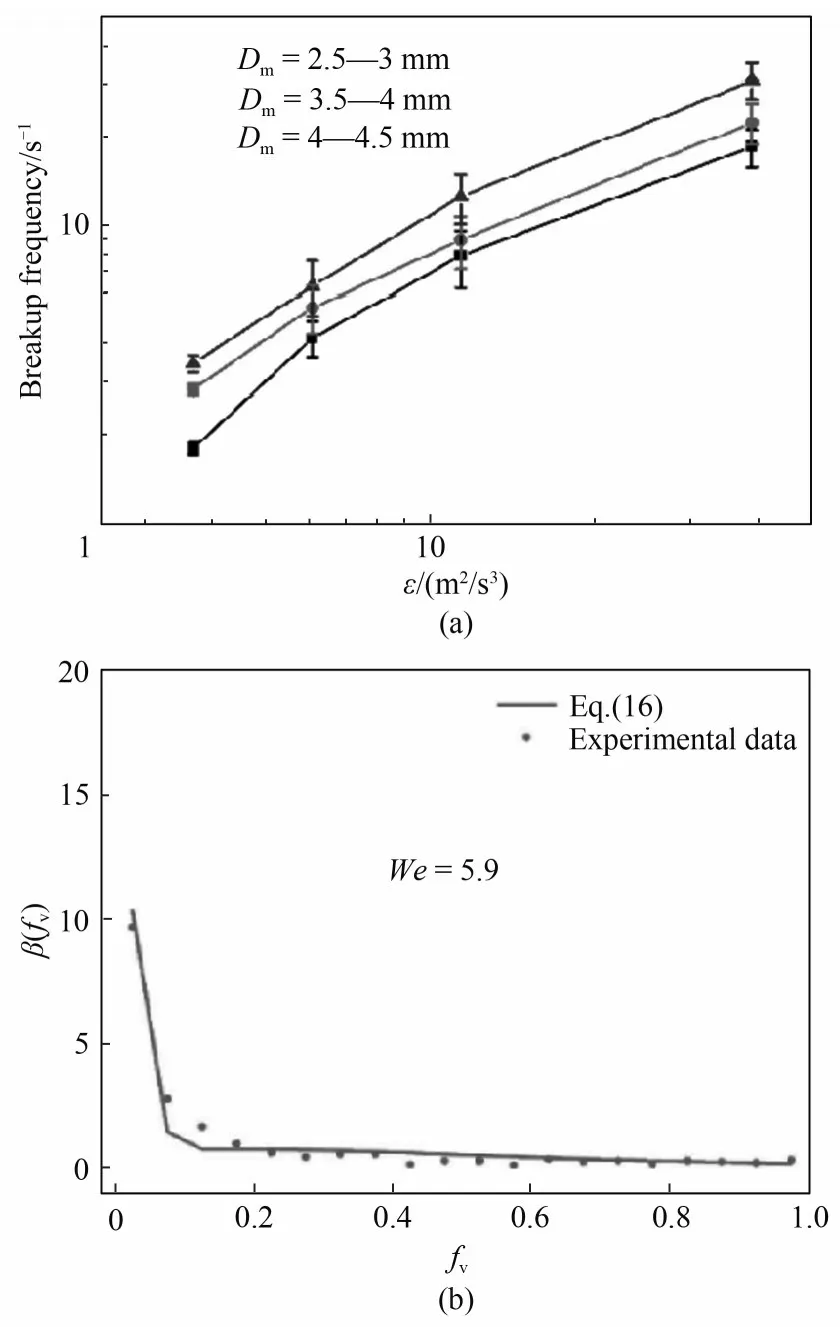
图10 气泡破碎速率和多重破碎子气泡分布[75]Fig.10 Breakage frequency and daughter bubble size distribution of binary bubble breakup[75]

2.2 采用内构件产生湍流

在该类方法中，通过加入内构件或者障碍物增加液相湍动，从而导致气泡破碎。Andersson等[35,46]在装有内构件的反应器内观察了气泡和液滴的破碎过程。实验由液体流经内构件产生湍流，由PIV测量湍流耗散速率ε，由高速相机在4000帧/s、30900pixel/cm2状态下记录气泡/液滴破碎过程。实验发现，气泡破碎过程不全是二元破碎的情况，还有三元和多元破碎发生，但二元破碎占95%以上；气泡和液滴破碎后子气泡/液滴大小分布分别呈现M形和Λ形；气泡/液滴破碎速率随母气泡/母液滴尺寸增加而增大。使用内构件，在较低流速下就可以产生强度较高并且较为均匀的湍流，拍摄照片清晰，但装置搭建较复杂。

Andersson等[46]通过实验观测到气泡变形过程中存在内部流动现象，这将影响母气泡破碎后子气泡大小的分布。如图11所示，气泡在湍流涡撞击后形成哑铃型的状态，即一个大气泡部分和一个小气泡部分，中间通过一个颈部连接。在附加表面张力作用下，气体从小气泡部分通过颈部流向大气泡部分，从而达到一个再分配的作用。

图11 气泡破碎成两个不同大小的碎片过程的照片[46]Fig.11 Images of breakup of a gas bubble into two fragments of different size[46]

2.3 搅拌产生湍流

在搅拌容器中发生机械搅动，以产生湍流从而破碎气泡[70-72]。文献中对液滴在搅拌槽中的破碎也作了较为深入的研究。在小型搅拌槽内发生气泡破碎操作简单，且无液体循环。但由于湍流的不均匀性较大，使得气泡由初始变形到最终破碎的整个过程所受到的湍流不均一，实验参数发生变化。气泡在搅拌器叶片附近比在其他区域更容易破裂。此外，气泡有时会因为刀片的切割而破碎。

Solsvik等[72]在圆柱形玻璃搅拌槽中进行了单气泡破碎实验。实验结果表明随着搅拌速度的增加，计算得到的湍流耗散速率增大，气泡破碎概率显著升高。同样地，随着母气泡大小从2.0mm增加到3.5mm，气泡破碎概率增加。另外，Solsvik等[72]发现非等大小破碎的概率远远高于等大小破碎概率。但是，该实验由于实验条件范围较窄，数据不具备可参考性，且气泡破碎时间与转速之间的关系也不明确。Hasan[70-71]通过搅拌槽内单气泡破碎实验发现，随着转速的增大，气泡破碎时间减小。但是，实验过程中测量的气泡直径较窄（2.2 ～4.0mm），气泡破碎时间与母气泡直径之间并没有统一关系。通过测量子气泡的数目，发现随着转速的升高，破碎得到的子气泡数目增加。另外，实验测量了离搅拌桨不同距离处的气泡破碎概率，结果发现离搅拌桨叶越近，气泡破碎概率越高，这也是由于离搅拌桨越近湍流越强所导致的。

Hasan[70-71]在一个带四挡板的圆柱形搅拌槽内进行了单气泡破碎实验研究，并测量了气泡破碎时间、破碎概率和子气泡数量。实验参数如下：气泡直径2.2 ～4.0mm，搅拌速度220～420r/min，拍摄速度2000帧/s。结果发现：随着母气泡大小和搅拌速率的增大，气泡破碎概率变大，但是等大小破碎概率降低，如图12所示。

图12 气泡破碎概率和等大小气泡破碎概率[70-71]Fig.12 Breakage probability and probability of equal-sized breakup[70-71]

Zhang等[76]设计了一种专为产生均匀湍流的圆柱形搅拌槽。系统研究了气体密度或压力（0.16 ～6.16 kg/m3）、液体性质（22.3 ～72.5mN/m,1～40mPa·s）、搅拌速度（480～640r/min）和母气泡尺寸（2.4 ～7.9mm）对气泡破碎时间、气泡破碎概率、破碎速率和子气泡大小分布的定量影响，实验结果如图13所示。结果表明，较高的搅拌速度、较高的气体密度或压力、较大的母气泡尺寸和较低的表面张力均可提高破碎速率；另外，在液体黏度μl≤8mPa·s时，气泡破裂速率与液体黏度无关，但随着液体黏度增大至40mPa·s，气泡破碎速率显著降低。

图13 气泡破碎速率[76]Fig.13 Bubble breakup rate at different liquid viscosities[76]

根据400组以上气泡破碎案例统计结果并且细化破碎分率间隔（Δfv=0.02），得到了一个典型的M形子气泡分布图，如图14所示。另外，较高的搅拌速度、较高的气体密度或压力、较大的母气泡尺寸和较低的表面张力均可提高等大小破碎的概率，如图15所示。此外，在实验中可以清楚地观察到气泡变形和破碎过程中的内部流动现象，并且发现气体密度越大内部流动速率越低，这也解释了高气体密度或者高压下气泡破碎速率增快的现象。图16显示了一个典型结果，相同时间段内，SF6母气泡变形形成的上端较小部分内的气体几乎没有流入到下端较大部分，且最终发生了等大小破碎。但是N2母气泡变形过程中形成了较长的气泡颈，气体快速从左侧较小气泡部分流入到右侧较大气泡部分，发生了非等大小破碎。通过计算发现，N2气泡的平均内部流速明显大于SF6气泡的内部流动的流速。

图14 M形子气泡分布[76]Fig.14 M-shape daughter bubble size distribution in a water-N2system at n=480r/min[76]

图15 子气泡分布[76]Fig.15 Daughter bubble size distribution[76]

图16 不同气体密度气泡变形破碎过程[76]Fig.16 Deformation and breakup of the bubbles with different gas densities(N2/water and SF6/water systems,db=4mm)[76]

2.4 圆锥反应器＆搅拌产生湍流

与搅拌槽内的液体流动相比，湍流管或锥形通道内的流动更为均匀，但湍流强度仍然较低；另外由于需要液体循环，所以实验装置比较复杂。

Wichterle等[73]在反应器中加了圆锥形隔板，反应器内液体由上向下流动，气泡在圆锥形区域上升速度缓慢，同时搅拌器产生的湍流涡撞击气泡发生破碎，用相机进行拍摄记录。Ravelet等[47]在类似装置中观察气泡的破碎过程，使用两台相机进行拍摄，可以更准确地确定气泡尺寸等信息。实验中母气泡直径（9.3 ±0.3 ）mm，气泡上升速度约300mm/s，相机视野高8cm、拍摄速度为300帧/s，湍动能由PIV装置测量。此工作中研究者将变形气泡发生破碎和不发生破碎的过程进行了对比。该类装置液体处在循环状态，气泡可以近似停留在拍摄观察区域，方便拍照，但对装置搭建要求较高。在该实验中，定性对比不同参数下气泡破碎速率大小或者定量测量气泡破碎速率还不够。

Zaccone等[77]也使用了此类反应器用于液滴破碎相关实验研究，最终获得了一个“Λ形”子液滴尺寸分布。但是，由于液滴破碎与气泡破碎有着显著的差异，该文不包含液滴破碎相关描述。

可以发现，目前文献中对气泡破碎的实验研究大多处于定性分析层面。具体气泡破碎和子气泡分布数据还相当匮乏。实验过程中使用的母气泡直径大多数处于2～5mm，但是较大尺寸的母气泡破碎形变过程尚未被拍摄。另外，当前的气泡破碎实验拍摄过程中均使用的是二维相机，无法得到详细的三维信息，因此未来三维层析拍摄技术在气泡破碎实验中需要得到充分应用。与此同时，更高压力下（≥1MPa），压力对气泡破碎的影响尚未得到清晰认知。其次，如何设计更加均质化的、湍流强度范围更宽的湍流在气泡破碎实验中显得尤为重要。在拍摄方面，高速相机的品质会影响气泡破碎实验的结果。例如，过低的拍摄频率导致相机无法捕捉临界气泡破碎的瞬间，从而导致记录的气泡破碎时间偏大。过低的分辨率会导致相机无法捕捉微小子气泡，从而使得气泡破碎概率偏低，以及子气泡破碎分布向高破碎分率偏移。因此，未来分辨率更高、拍摄速度更快的相机也将有利于气泡破碎实验研究的发展。

3 气泡破碎速率计算值与实验值对比

3.1 常压对比

通过将气泡破碎速率的模型计算值和实验测量值进行对比，可以对模型进行验证。图17显示了常压条件下模型预测的无量纲化气泡破碎速率与文献中无量纲化实验数据的对比情况。无量纲变量定义为：

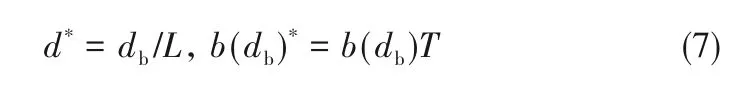
其中，L和T分别为长度和时间尺度，定义为：

从 图17可 以 看出，Wang等[11]、Razzaghi等[33]和Zhang等[42]的气泡破裂模型预测值与实验值相符。而Luo等[26]的破碎模型和Xing等[38]的模型低估了较大气泡尺寸范围内的破碎速率(db*＞1)，Zhao等[34]的模型低估了小气泡尺寸范围内的破碎速率(db*≤1)。

图17 预测和测量气泡破碎速率的比较[42]Fig.17 Comparison of predicted and measured bubble breakup rate[42]

3.2 高压对比

目前文献模型中仅有Zhao等[34]、Xing等[38]和Zhang等[42]的模型考虑了压力对气泡破碎的影响。Wilkinson等[60-61]和Zhang等[76]实验均发现压力升高，气泡破碎加快。

Andersson等[35,46]以及Ravelet等[47]利用高速摄像机研究了气泡破碎行为，均发现气体可以快速流过变形气泡的颈部。因此，本课题组基于内部流动机制建立了气泡破碎模型[38]。该模型通过考虑气泡变形过程中由于压力差引起的内部流动，建立相关的内部流动方程，从而正确预测压力对气泡破碎的影响规律，如图18所示。然而该模型预测的气泡破碎速率严重低于实验结果，如图19(a)所示。后期，本课题组根据文献中报道气泡颈部缩小到一定程度即发生破碎，改进了前期建立的内部流动模型，成功从趋势上和数量上预测了压力对气泡破碎速率的影响规律，如图19(b)所示。

图18 压力对气泡破碎概率的影响[42]Fig.18 Comparison of predicted and experimental breakup percentage for different mother bubble sizes(σ=0.072 N/m,ε=2.0m2/s3)[42]

图19 压力对气泡破碎速率的影响[42]Fig.19 Effect of pressure or gas density on breakup rate b(db)(σ=0.072 N/m,ε=2.0m2/s3)[42]

在后期气泡破碎实验阶段，利用测量的实验数据对改进的内部流动模型进行了验证，结果发现该模型可以很好地预测各种参数例如压力、物性参数、母气泡大小和湍流耗散速率对气泡破碎速率的影响，如图13所示。

4 结论与展望

通过对气泡破碎模型和气泡破碎实验进行汇总、分析和总结，发现近些年来气泡破碎建模和实验研究均不断改进和完善，主要进展有以下几点：

（1）气泡破碎模型中考虑了更加复杂的物理现象例如内部流动现象、多重破碎，包含了更多的物理机制例如湍流全能谱、气泡复杂形变过程和气泡-湍流涡碰撞角度方向等；

（2）气泡破碎模型可以预测更宽的操作条件和物理性质的影响，例如高压或高黏度液体体系；

（3）气泡破碎实验从以往气泡变形破碎过程的简单观测到定性和定量测量气泡破碎过程中的气泡破碎时间、气泡破碎概率、子气泡数目和子气泡概率分布情况，并计算出气泡破碎速率。

然而，关于气泡破碎建模和气泡破碎实验设计还存在较多问题，需要进一步完善：

（1）建立计算过程更加简便的、能够对操作条件和物理性质变化具有普适性的气泡破碎模型；

（2）能够定量描述母气泡大小、湍流耗散速率、体系压力、液体黏度和表面张力对气泡破碎过程中各个变量例如气泡破碎时间、气泡破碎概率、子气泡分布以及气泡破碎速率影响的实验数据极其缺乏。因此，如何更有效合理地设计气泡破碎实验还需进一步突破。

符号说明

b(v),b2(d),

b(db)——气泡破碎速率，s-1

b(db)*——无量纲化气泡破碎速率

CD2——帽状/段塞气泡曳力系数，m

C7，C8，C9——破碎模型参数

C21,C22,C23——Sun经验关联式模型参数

CⅠ,CⅡ——破碎模型参数

Ca——毛细管数

c(v)——气泡聚并速率，s-1

Dc——气泡体积当量直径，m

DⅠ——搅拌叶轮直径，m

DF(ϕ)——涡流阻尼因子

d,db——母气泡直径，m

d*——无量纲化气泡直径

dc2——界面不稳定导致破裂的气泡临界尺寸，m

ds——剪切破碎后子气泡平均尺寸，m

ds,max——剪切破碎后子气泡最大尺寸，m

d1——湍流涡波动和碰撞破碎后最小子气泡直径，m

Ec——气泡破碎所需能量，kg·m2/s2

e——单个湍流涡能量，kg·m2/s2

fv——气泡破碎分率

fL(κL)——能量保持区无量纲函数

fη(κη)——能量耗散区无量纲函数

G——流道间隙，m

Kg——破碎模型模型参数

K1，K2——破碎模型模型参数

L——长度尺度，m

N*——搅拌速度，r/s

n(v,t)——气泡数量密度函数，m-3

P(db)——气泡破碎概率

RC——曲率半径,m

S——气泡表面积，m2

T——无量纲化时间尺度

T1,T2,

T3,T4,T5——全能谱模型参数

tb——气泡破碎时间，s

ub——气泡速度，m/s

uci——气泡破碎临界湍流涡速度，m/s

ute——湍流涡速度，m/s

VSO——剪切气泡的体积，m3

v——母气泡体积，m3

v′——子气泡体积，m3

vr——气体流速，m/s

W——流道的较长宽度，m

We,We1——Weber数

Wecr,Wec——临界Weber数

αg——气含率

α2——帽状/段塞气泡体积分率

β——模型参数

β(v)——气泡尺寸分布

γ——内部流动参数

γSO——Ishii经验关联式模型参数

δeff——气膜有效厚度，m

ε——湍流耗散速率，m2/s3

κ——湍流涡波长，m-1

λ——湍流涡尺寸，m

μg——气体黏度，mPa·s

ξ——湍流涡尺寸与母气泡尺寸的比值

ξSO——剪切生成子气泡平均尺寸与最大尺寸的比值

ρg——气体密度，kg/m3

ρl——液体密度，kg/m3

σ,τs——液体表面张力，N/m

σv——标准偏差

τv——黏性剪切应力，N/m

ΦSI——界面面积密度源项，m-1·s-1

ω——气泡湍流涡碰撞频率，m-3·s-1