荧光光谱无用散射的自动去除算法
2022-01-10许佩军张明振郭秋含牟晓红
许佩军, 周 末, 张明振, 郭秋含, 牟晓红, 李 焱
(1.辽宁师范大学 物理与电子技术学院,辽宁 大连 116029;2.中国科学院 大连化学物理研究所 分子反应动力学国家重点实验室,辽宁 大连 116023)
三维荧光光谱是近些年广泛应用而发展起来的一种荧光分析技术, 它在食品科学[1-2]、分析化学[3-6]、生物化学[7-8]以及环境科学[9-10]等领域都有广泛的应用. 三维荧光光谱是由激发波长(Emission, Em), 发射波长(Excitation, Ex), 荧光强度(荧光强度数值用Z表示)组成的三维矩阵光谱(Excitation-Emission Matrix, EEM), 它描述了荧光强度随激发波长和发射波长的变化关系. 三维荧光光谱不仅能够获得激发波长与发射波长, 同时能够获取变化时的荧光强度信息. 在荧光光谱的生成过程中, 由散射机制引起的拉曼(Raman)散射或瑞利(Rayleigh)散射, 经常会单独存在或同时存在于荧光光谱数据中. 这两种散射的能量通常要高于目标物质对应的能量. 而且, 这两种散射的能量范围有可能干扰甚至部分覆盖目标物质的能量, 于是, 去除荧光光谱中的无用散射就具有重要的理论研究意义.
无用散射的去除工作, 一直是荧光光谱分析工作中的重要步骤[11-13]. 2014年, Eilers和Kroonenberg通过高斯峰刻画了散射的位置信息、高度以及宽度. 在平滑处理后, 实现拉曼和瑞利散射的去除[14]. 2015年, Rinnan和Anderson对荧光光谱数据中的拉曼和瑞利散射进行去除[15]. 2015年,Elcoroaristizabla和Bro等人对荧光光谱数据处理的相关工作进行了总结[16]. 2019年,Chiappini、Alcaraz和Goicorchea等人提出改进的信息保守方法用于处理荧光数据中的拉曼和瑞利散射[17]. 2019年, Chiappini等人基于已有的算法, 给出处理荧光光谱数据的图形交互界面, 这使得即使没有程序语言基础, 也能够轻松实现光谱数据的处理[18].
上述工作中, 对无用散射的判断, 大部分是在Ex方向上基于高斯分布判断散射的宽度, 高度等信息. 当散射能量不满足对称或高斯分布时, 散射的信息便有待进一步确定. 本文旨在提出一种基于数据自动判断无用散射的机制, 在完成去除后, 通过剩余数据对删除数据实现补全. 这一算法对荧光光谱数据并无高斯分布的要求.
1 去无用散射算法
在光谱数据中, 瑞利散射满足
Em=n×Ex,
(1)
其中,n代表n阶散射.
在光谱数据中, 拉曼散射满足
(2)
其中,wnr是光谱数据中瑞利散射和拉曼散射的波数之差.
在无用散射去除过程中, 荧光光谱需要满足如下两条件要求:①瑞利和拉曼散射的能量大于目标物质的能量;②瑞利和拉曼散射至少存在一种. 在Em方向中,散射能量不要求为高斯分布. 最高值可以为定值. 无用散射的去除过程有3个主要步骤:①数据预处理及散射判断;②散射信息处理以及散射去除;③去除补齐.
在对光谱数据实现预处理和散射判断的过程中, 由于生成机制所致, 荧光光谱中会存在大量的散点噪声, 这使得光谱的能量并不平滑, 会影响之后的无用散射信息的判断准确性. 于是, 在本文提出的算法中, 通过2D的均值滤波实现平滑处理, 在基本保留荧光光谱的主要信息的前提下, 去除此类噪声. 具体的, 如下式所示:
(3)
其中,ni、nj分别是在2D数据中沿Ex、Em方向上的平滑宽度.
在荧光光谱的数据中, 通过能量值判断瑞利或拉曼散射是否存在. 根据两种散射的理论基础, 两者在光谱中的位置基本固定, 需要确定的是必须去除的无用散射宽度.
本文的思路是通过迭代的方式, 在一定范围不断选择能量高的数据, 通过最小二乘法拟合出直线方程.当直线方程在散射的范围之内, 则认为存在散射;若直线方程不在散射的范围之内, 有可能是因为选取能量高的数据点过少, 则需放宽能量点的选择范围, 筛选更多的能量点, 通过上述的方法直至拟合出在散射范围内的直线方程. 具体的判断流程如图1所示.

图1 无用散射的确定过程流程图Fig. 1 The flowchart of detecting the useless scatter
对于光谱数据, 通过针对每个Em值上不同Ex对应的强度Z, 实现散射宽度的确定. 首先, 通过一维数据说明无用散射的信息确定过程. 如图2(A)显示的是特定Em值, 强度Z随Ex的变化的数据. 由于已经经过2D的平滑处理, 强度曲线中已经不存在散点噪声, 但曲线依旧不平滑. 本文采用1D的平滑处理, 使曲线保持其原有的变化趋势, 但能平滑掉细小的凹凸不平, 具体的如图2(B)所示. 因为Em已知, 根据之前确定的散射方程, 可以得到无用散射的峰值的粗略范围,Sp在本论文中同时考虑曲线的一阶导数和二阶导数判断散射峰的范围.
针对平滑后的数据求解能量强度Z, 对于Ex的一阶导数和二阶导数, 分别在图2(C)和图2(D)所示. 其中,距离Sp最近的一阶导数为0的点为无用散射的宽度范围,二阶导数为0的点用于进一步判断宽度范围是否准确.

图2 无用散射信息确定过程的示意图Fig.2 The illustration of deciding the range of useless scatterA.随Ex的变化的2D平滑后的强度值(特定Em);B.1D平滑后的强度值;C.强度的一阶导数变化;D.强度的二阶导数变化
在确定无用散射的宽度后, 将在确定的无用散射范围内的强度值设为空(NaN).
在去除无用散射的能量后, 通过插值的方式, 将NaN区域进行补齐, 以确保荧光光谱的完整性. 本文中采用的是三次多项式的插值实现.
对于一个特定Em值对应的能量曲线, 分别针对拉曼和瑞利散射实现上述过程, 完成单条能量曲线上的两种无用散射位置的补齐. 对于每个Em值均完成上述处理, 即完成整个光谱的无用散射的处理工作.算法的流程图如图3所示.对数据的处理示意图如图4所示.

图3 三维荧光光谱数据去除无用散射的实现步骤Fig. 3 The steps of deleting the useless scatter in 3D EEM fluorescence
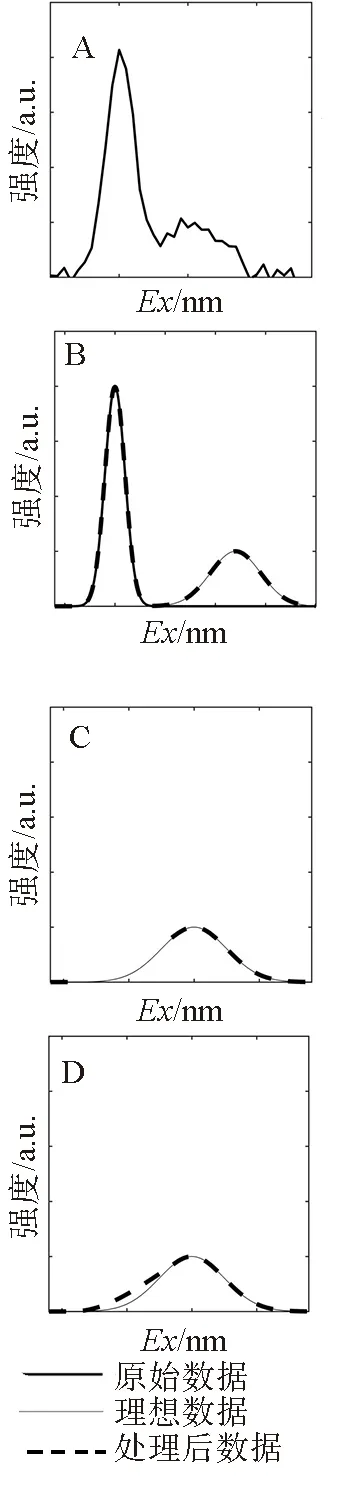
图4 三维荧光光谱数据去除无用散射的实现流程图Fig. 4 The illustrations of deleting the useless scatter in 3D EEM fluorescence
2 测试光谱生成
针对新的去散射算法, 完全基于实验所采集的光谱数据进行验证需要消耗大量的资源. 并且由于真实的实验环境所限, 绝大部分的实验过程都无法保证实验所使用数据的完备性, 于是本文尝试使用依据理论生成的荧光光谱数据来验证所提算法针对不同特点数据的鲁棒性.
首先, 对于要生成的光谱数据, 确定其中目标能量的位置. 如前所述, 在光谱数据中拉曼瑞利两种散射生成机制相对固定, 其中,不同谱之间无用散射改变的是其对应的长度、宽度、强度和分散程度等性质. 为了与现实中的光谱数据更加接近, 在生成谱的过程中还在数据中加入散点噪声和半径小于Rnoise的圆形噪声. 为了验证所提算法对无用散射和目标能量的区分能力, 针对上述信息随机生成具有不同性质的无用散射的光谱数据.
将目标物对应的能量生成在光谱数据的有效范围中, 其中, 拉曼散射和瑞利散射包围范围之外的部分不生成目标物的能量, 目标物的能量采用ntag个二维高斯分布代替. 其中,σ1,σ2在一定的范围内选取在本数值实验中选择ntag=1,2,3.
目标散射和无用散射基本存在三种位置关系, 分别是相距较远, 部分相交和部分覆盖.
在图5(A)中显示的是目标物的能量与两种散射均不相交的情况.在图5(B)中显示的是目标物的能量只部分与散射相交且散射的能量覆盖目标物能量. 在图5(C)中显示的是目标物的能量散射能量覆盖目标物.图5(D)~图5(F)分别对应着子图5(A)~图5(C)中固定Em值能量强度对应Ex的变化过程. 基于生成的荧光光谱数据,采用本文提出的去噪算法,会得到去除无用散射后的光谱数据.针对三种不同的情况,分别生成若干个测试用光谱数据,图6~图8分别针对每种情况选择三组数据用于显示和说明.每个图的子图中,左侧子图是依据理论生成的光谱数据,侧子图是去散射之后,目标能量的分布.由于目标能量相比于无用散射低所以一般的右图中的能量范围要小于左图中的能量范围.三种情况中,本论文算法均能很准确地判断无用散射的位置和能量,实现无用散射的去除和补全.

图5 目标能量和无用散射的位置关系Fig. 5 The position relationship of target energy and useless scatterA.目标物的能量与无用散射均不相交的三维光谱图;B.目标物的能量只部分与无用散射相交的三维光谱图;C.无用散射能量覆盖大部分目标物能量的三维光谱图;D.基于A图数据下固定Em值能量强度对应Ex的变化过程;E.基于B图数据下固定Em值能量强度对应Ex的变化过程;F.基于C图数据下固定Em值能量强度对应Ex的变化过程
具体如图6所示, 目标能量在散射之间, 且分别距离两种散射较远, 这使得对无用散射的判断不受目标能量影响, 容易确定其覆盖范围. 于是, 具有较高能量的无用散射被剔除后, 基本没有影响目标物的能量. 在三组生成的光谱数据中, 所提算法均很准确地实现了无用散射的剔除.

图6 去无用散射前后光谱数据的对比图. 目标能量和无用散射相距较远Fig. 6 The comparison between the fluorescence data before and after deleting the useless scatter. Large distance between target energy and useless scatter
在下面的各个光谱数据图像中, 横轴为Em, 纵轴为Ex, 光谱强度以等高线的形式显示, 激发波长和发射波长单位为nm,光谱强度单位为a.u.,其中,等高线颜色对应的光谱强度由每个子图右侧的colorbar显示. 之后生成的光谱数据、实验数据的图像均以此种方式表达.
如图7所示, 当目标能量存在一部分与无用散射相交的情况时, 目标能量对无用散射的判断也产生影响, 但这种影响相对于无用散射的高能量, 基本可以忽略. 目标能量中, 能量较低的部分由插值得到. 于是, 本文所提算法依旧可以准确地实现无用散射的剔除.

图7 去无用散射前后光谱数据的对比图.目标能量和无用散射部分相交Fig.7 The comparison between the fluorescence data before and after deleting the useless scatter. Partly intersection of target energy and useless scatter
如图8所示, 部分的目标能量与无用散射重叠, 这使得对无用散射的范围的判断难度提升. 在目标能量中, 存在一部分通过插值得到的数据, 但根据光谱数据进行插值, 可以确保保留目标物的能量变化趋势, 于是, 所提算法还是可以准确实现无用散射的剔除.

图8 去无用散射前后光谱数据的对比图.目标能量和无用散射部分重叠Fig.8 The comparison between the fluorescence data before and after deleting the useless scatter. Partly overlapping of target energy and useless scatter
3 实验光谱的去无用散射
通过生成的荧光光谱可以验证所提算法的可行性. 下面将该算法用于实验过程中得到的真实的光谱数据中.
对比于生成的光谱数据, 真实的荧光光谱数据具有更强的随机性, 其中目标函数的范围也更加的不规则, 这给去除无用散射增加了难度.
如图9所示, 在光谱数据中, 目标能量覆盖的范围更大, 且只存在一组无用散射的影响. 对于每个Em值, 判断无用散射的难度加大. 但由于散射与目标能量相互独立, 所以所提算法很准确地去除了无用散射, 并保留下大范围的目标能量.
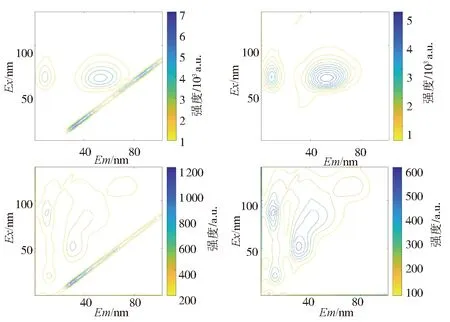
图9 去无用散射前后光谱数据的对比图. 目标能量和无用散射相距较远(实验数据)Fig.9 The comparison between the fluorescence data before and after deleting the useless scatter. Large distance between target energy and useless scatter(experiment)
如图10所示, 目标能量有一部分与无用散射相交, 而且无用散射以很高的能量影响目标能量. 即便如此, 目标能量也被准确的保留, 得到较好的无用散射去除结果.

图10 去无用散射前后光谱数据的对比图.目标能量和无用散射部分相交(实验数据)Fig.10 The partly intersection of target energy and useless scatter (experiment). Partly intersection of target energy and useless scatter
4 结 论
本文提出一种基于光谱数据判断无用散射的去除算法. 针对生成的光谱数据和实验得到的光谱数据, 均得到了较好的无用散射去除效果, 本算法为进一步的高通量自动去除无用散射提供可能. 本文所提出的算法, 暂时只针对一阶瑞利和拉曼散射. 在未来的工作中, 如何基于现有机制实现高阶无用散射的去除, 是我们要进一步研究和探讨的主要内容.
