一种基于列车群分布的高效等间隔行车调整方法

黎邓根，梁 烨，肖习雨，李娟娟

（株洲中车时代电气股份有限公司，湖南 株洲 412001）

0 引言

列车等间隔调整是一种在突发情况时使用的特殊行车指挥方式，其通过合理地规划列车停站时长和运行等级，使列车之间的追踪间隔保持一致。列车在运营途中可能会发生一些突发状况，如正在运营的城市轨道交通列车发生故障，故障列车将在原地停留直至故障被修复，这可能导致其他列车的严重早晚点到达，运行图严重紊乱；又如，车站周边发生火灾、泥石流等自然灾害，列车无法经过该站，只能在不经过该站的小交路上行车。在这些情况下，列车无法按原有运行图行驶，而通过等间隔调整可简单、有效地恢复运营秩序[1]，大大减少调度人员的工作量。

目前存在多种等间隔调整方法，但大部分方法[2-4]没有考虑全体列车的分布情况，只是考虑本车与前后几辆车的间隔，根据实际间隔与理想间隔的差异进行调整。以文献[2]为例，其根据前后两车在相同站台到站时间之差计算追踪间隔，再对后车的停站时间、运行时间进行调整，使两车的间隔更接近理想追踪间隔。文献[5]局部考虑了前后车间隔，并根据列车群在半个交路上的疏密程度对列车整体分布情况进行了粗糙考虑，但方法较为复杂，实现的难度较大。文献[6]首先选择列车数最多的区间并将其最中间的列车作为参考车，然后根据其他车与参考车的实际间隔与理想间隔的差异进行调整，这种方法较好地考虑了列车整体分布情况，但如果站台多列车少，选取的参考车不一定合适。目前已有的方法都没有以调整效率为优化目标，虽然能实现等间隔行车效果，但调整效率可能不够理想。

为了弥补上述各种方法的不足，本文基于全体列车的分布情况，以调整阶段的时长为优化目标，设计了一种新的等间隔行车调整方法。

1 等间隔行车调整方法

1.1 方法介绍

等间隔行车调整的目标是使每辆列车之间的追踪间隔保持一致，该目标可抽象化地表示为图1所示。图中，大圆的周长为列车按默认停站时长和默认运行时长行驶完一个交路所需的时长，一个小圆点为一辆列车，其顺时针方向的下一个圆点为其行驶方向的前一辆列车，圆点之间的边长为列车之间按默认方式行驶的追踪间隔。图中左侧大圆被称为“初始状态圆”，其表示初始状态列车在时间维度的相对位置；右侧大圆被称为“等间隔状态圆”，其表示等间隔行驶状态列车在时间维度的相对位置。等间隔调整的目标就是将混乱的左侧大圆调整至均匀分布的右侧大圆。

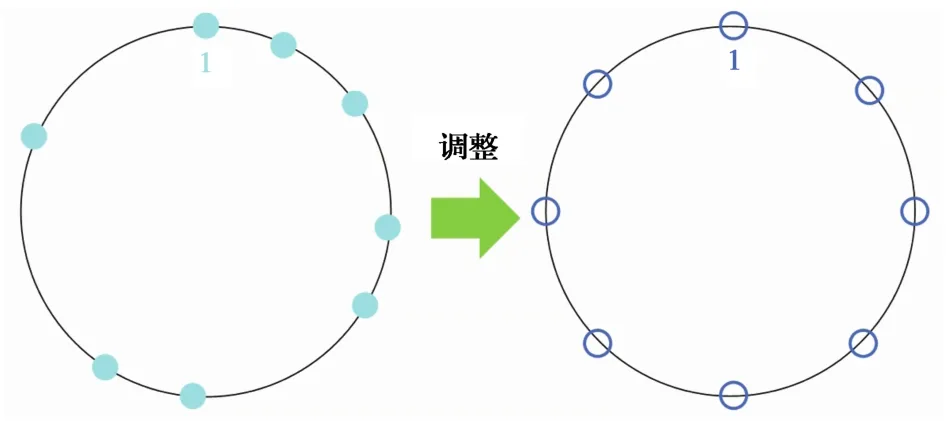
图1 等间隔调整目标的抽象表示Fig. 1 Abstract representation of constant train regulation target

若要移动小圆点在大圆上的位置，只能通过改变停站时长和运行时长。在默认时长的基础上，增加停站时长和运行时长，列车与前车间隔将被拉大，与后车的间隔将变小，因此小圆点逆时针移动；同理，缩短停站时长和运行时长，小圆点顺时针移动。需注意，应限制停站时间的可调整范围（因为停站时间过短，乘客可能来不及上下车；停站时间过长，乘客可能会产生焦虑感）[7]；且每个站台客流量不一样，因此需合理设置每个站台的最小、最大停站时间。

将初始状态圆和等间隔状态圆重叠在一起，如图2所示。可清楚地看出，每辆车需要调整多少时长才能从初始状态(实心点)变为理想等间隔状态(空心点)。待调整时长被定义为，列车从初始状态至理想等间隔状态的过程中，在每个站台的停站时长和每个区间的运行时长相对于默认时长的改变量之和。若待调整时长为正数，则需要增加停站时长、或通过调整运行等级增加运行时长；若待调整时长为负数，则需要减小停站时长、或通过调整运行等级减小运行时长；若待调整时长为零，则不需要调整。

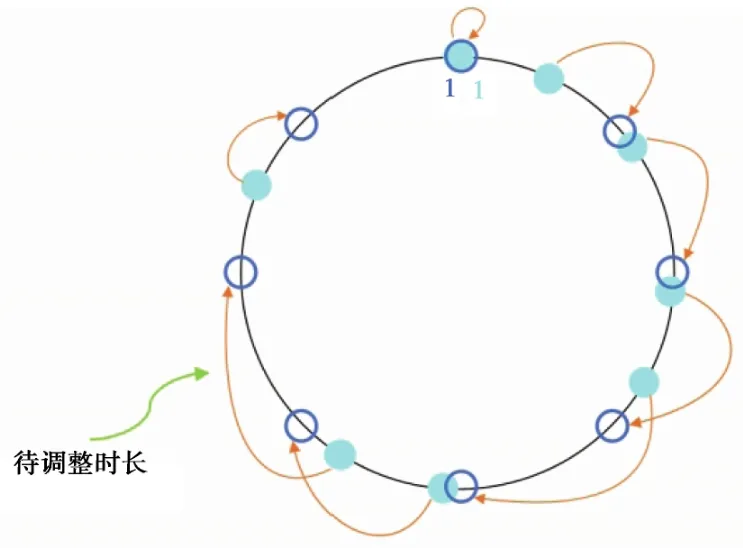
图2 由初始状态调整至等间隔状态Fig. 2 Adjust from the primary status to constant status

本文所提的等间隔行车调整方法可分为3步：首先计算列车之间的追踪间隔，得到初始状态圆；然后通过旋转等间隔状态圆，求得每辆列车的最优待调整时长；最后，通过调整停站时长和运行等级将每辆列车的待调整时长调整至零。

1.2 计算列车追踪间隔

绘制如图3所示的城市轨道交通列车运行模型图，具体设置如下：

图3 列车编号和站台编号示意图Fig. 3 Schematic diagram of train number and platform number

（1）列车的数量为N，编号分别为1,2,…,N，其中2车在1车运行方向的前方，3车在2车运行方向的前方，以此类推。

（2）站台的数量为M，编号分别为1,2,…,M，每个编号对应上行或下行的一个站台，M个站台组成一个运行交路，在列车运行方向上，2站在1站前方，3站在2站前方，以此类推。

（3）N车运行方向的前一车为1车；M站运行方向的前一站为1站（M站是上行方向的终点站，列车在该站完成折返后前往下行方向的起始站）；(i+1)车为i车的前一车；(i-1)车为i车的后一车；(j+1)站为j站的前一站；(j-1)站为j站的后一站。此规则同样适用于求和表达式中。

（4）j区间表示j站至(j+1)站之间的区间。

（5）折返站的停站时长为折返时长。

从自动列车监督系统（automatic train supervision system，ATS）[8]获取以下信息：列车当前处于停站状态或是运行状态、所在站台/区间、计划停站/运行时长、已经停站/运行的时长以及所有站台的默认停站时长和区间的默认运行时长。根据这些信息，可以计算出列车下次到达某站台的预计时间Pv。

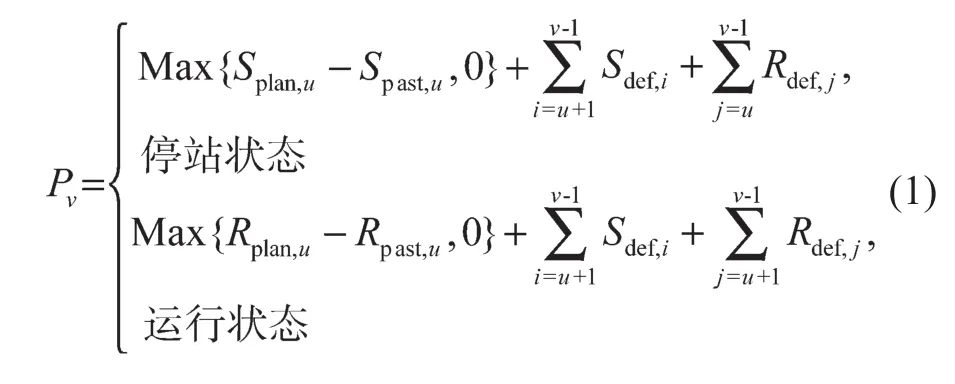
式中：v——预计到达站台的编号；u——当前所在站台/区间编号；Splan,u——u站台的计划停站时长；Spast,u——u站台已经停站的时长；Rplan,u——u区间的计划运行时长；Rpast,u——u区间已经运行的时长；Sdef,i——i站台的默认停站时长；Rdef,j——j区间的默认运行时长。

通过这种方法计算后车预计到达前车前方站台的时间，再计算前车预计到达其前方站台的时间，两者差值即为两车的追踪间隔。

得到每两辆车之间的追踪间隔后，假定1车位于初始状态圆的最上方，则容易得到其他列车在初始状态圆上的位置。

1.3 计算最优待调整时长

若将等间隔状态圆进行旋转，每辆车的待调整时长发生改变。从图4中可直观地看出，旋转等间隔状态圆之后，大部分列车待调整时长的绝对值减小了，能更快达到等间隔效果（图4右下角所示状态实现等间隔行驶的难度明显低于图4左下角）。因此存在一个最优的等间隔状态（通过第一辆车的待调整时长τ1体现），使列车群以最短的时长完成等间隔调整。

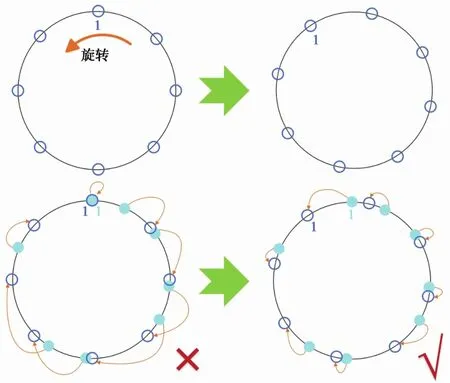
图4 旋转等间隔状态圆对待调整时长的影响Fig. 4 Effect of rotating the constant status circle on the time to be adjusted

如果确定了第一辆车的待调整时长τ1，则易求得其他车的待调整时长：

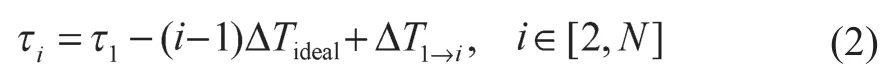
式中：ΔTideal——理想追踪间隔，，其中Tperiod为按默认方式行驶完一条交路所需的时长；ΔT1→i——1车至i车的追踪间隔。

若已知列车的待调整时长τ，可估算出将该车的待调整时长调整至零所需要的时长G：

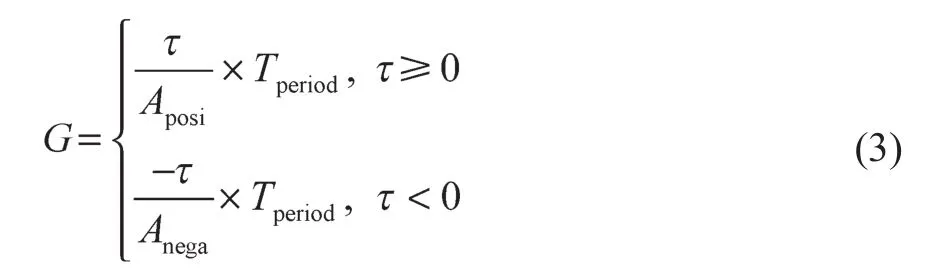
其中，Aposi和Anega分别为列车行驶完一条交路最多能增加和减小的停站时长以及运行时长，其计算分别为

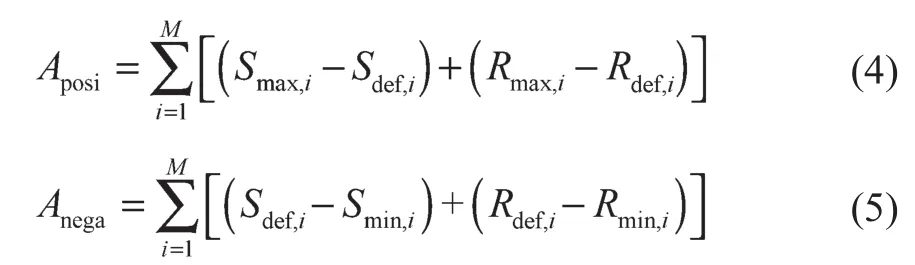
式中：Smax,i——i站台的最大停站时长；Smin,i——i站台的最小停站时长；Rmax,i——i区间的最大运行时长；Rmin,i——i区间的最小运行时长；Rdef,i——i区间的默认运行时长。

当最后一辆车的待调整时长调整至零时，列车群才实现等间隔行驶，因此，优化目标为

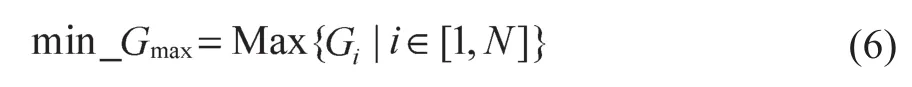
式中：Gmax——列车群中最大的时长。

计算最优待调整时长流程如图5所示，图中best_τi为最优状态时列车i的待调整时长，min_Gmax为最优状态时的Gmax。

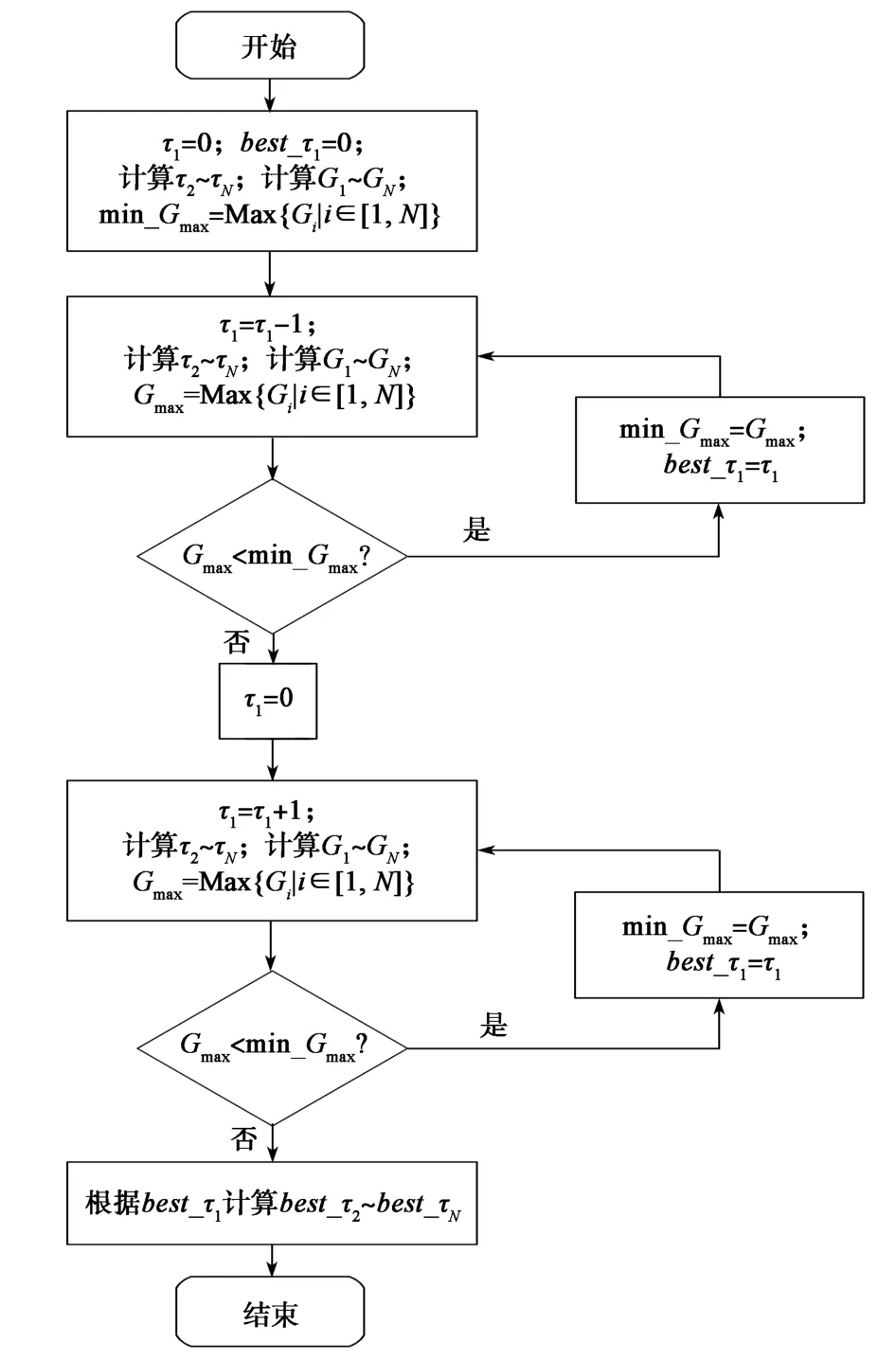
图5 计算最优待调整时长流程Fig. 5 Flow chart for calculating the best time to be adjusted

1.4 调整策略

每次当列车到达某一站台（假设为k站台）时，首先更新该列车的待调整时长：

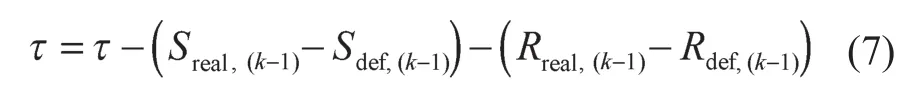
式中：Sreal,(k-1)——列车在(k-1)站台实际的停站时长；Rreal,(k-1)——列车在(k-1)区间实际的运行时长；Sdef,(k-1)——(k-1)站台的默认停站时长；Rdef,(k-1)——(k-1)区间的默认运行时长。

然后通过式(8)计算列车在k站的计划停站时长和在k区间的计划运行时长。

式中：Splan,k——k站台的计划停站时长；Sdef,k——k站台的默认停站时长；Rplan,k——k区间的计划运行时长；Rdef,k——k区间的默认运行时长；Smin,k——k站台的最小停站时长；Smax,k——k站台的最大停站时长；l——运行等级，假设存在5个运行等级；Rk,l——按运行等级l在区间k行驶所需的运行时长。

计算完计划停站时长和运行等级后，通过ATS将计划下发给列车执行。经过时间迭代，列车的待调整时长的绝对值将逐渐减小；当每辆车的待调整时长调整至零（或接近于零）时，列车群即实现了等间隔行驶。

此外，每隔一段时间，如5 min，可重新按1.2节、1.3节和1.4节所示方法计算各列车的最优待调整时长，以修正因列车追踪间隔计算不准、真实停站/运行时长获取不准等而造成的系统误差。

2 仿真验证

本文通过开发城市轨道交通列车运行的仿真程序来模拟所提方法实现等间隔行车调整的过程，并与其他方法进行比较。

2.1 本文方法

为了检验本文所提方法的可用性，设计了图6所示5种仿真场景：

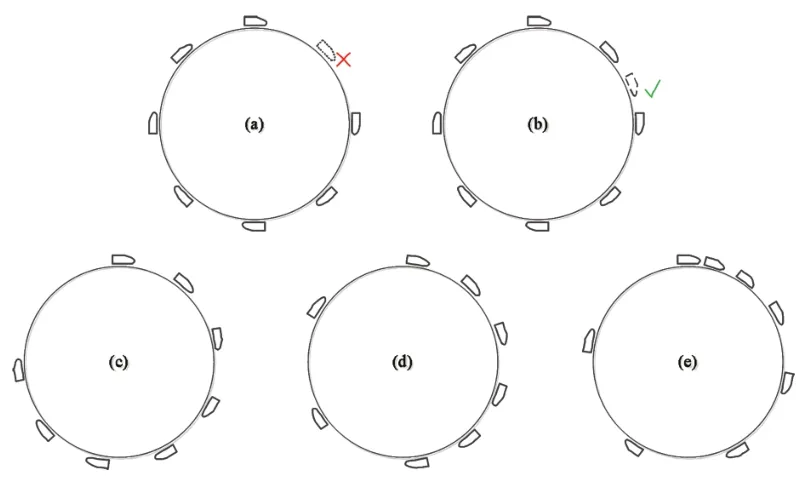
图6 仿真场景Fig. 6 Simulation scenarios

（a）在列车均匀分布的前提下减车；

（b）增车；

（c）因堵塞导致所有列车在3/4交路上均匀分布，在另外1/4交路上无列车；

（d）在1/2交路上均匀分布75%的列车，在另外1/2交路上分布剩下25%的列车；

（e）列车间的追踪间隔呈等差分布。

分别仿真模拟15, 20和25辆列车在长沙地铁4号线上的行驶过程。根据以上5种场景设置列车的初始位置，假定列车的默认运行等级为普速。使用本文所提等间隔调整方法，使列车群达到等间隔行驶效果（每辆车之间的追踪间隔和理想追踪间隔的偏差小于30 s）所需的时长如表1所示。

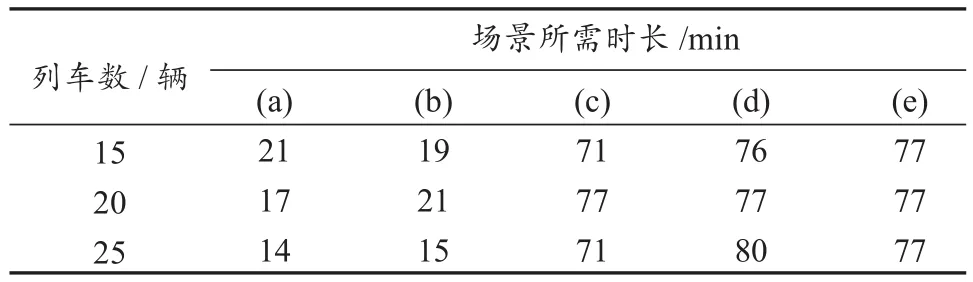
表1 仿真结果Tab. 1 Simulation results

由图6和表1可以看出，对于增减车场景（即场景(a)和(b)），列车群能在20 min左右达到等间隔效果；对于堵塞场景（即场景(c)和(d)）和离散分布场景（即场景(e)），列车群也能在80 min左右达到等间隔效果，少于行驶一个上行过程所需时长（约100 min），等间隔调整的效果较好。

为了直观地展示等间隔效果，画出20辆列车在场景(e)的运行线，如图7所示。可以看出，随着时间的迭代，列车间的间隔越来越均匀。

图7 本文所提方法的仿真运行线Fig. 7 Simulated running line by this method

2.2 与其他方法的比较

为了体现本文所提方法的高效性，将本文方法与前后车平均间隔法及前车到站时刻判断法[2]进行对比分析。

2.2.1 前后车平均间隔法

某列车到站时，使用前后车平均间隔法计算该车与其前后车的追踪间隔，以调整该车在当前站台的停站时长和下一区间运行等级，使其与前后车的追踪间隔尽可能相同。每次列车到站都如此处理，直至列车群达到等间隔行驶效果。

采用这种调整方法，对处于场景(e)的20辆车进行仿真模拟，大约需要150 min才能达到等间隔行驶效果，运行线如图8所示。

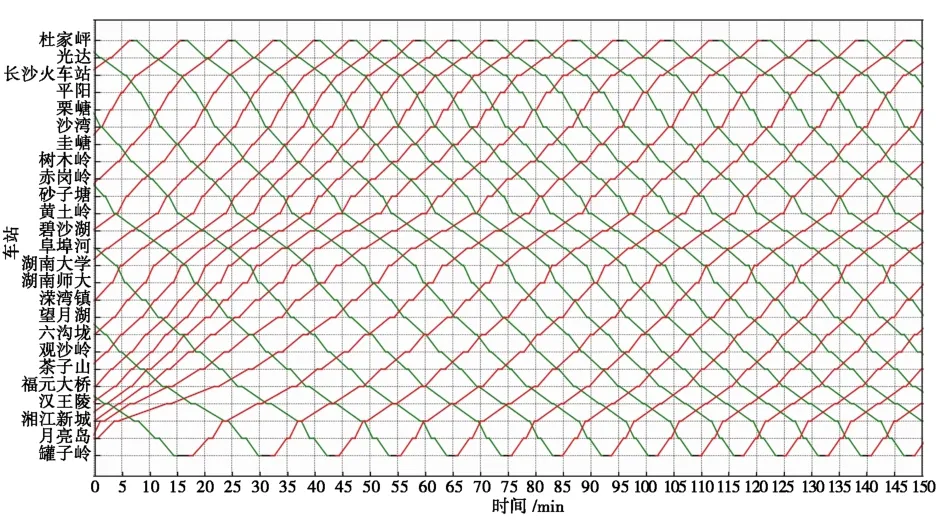
图8 前后车平均间隔法的仿真运行线Fig. 8 Simulated running line by the method of average interval between previous and next trains

从图8可看出，列车群缓慢地达到等间隔状态，与本文所提的方法相比，需要双倍的时间才能达到等间隔效果。

2.2.2 前车到站时刻判断法

某列车到站时，用前车在该站的到站时间减去当前时间，得到与前车的追踪间隔，以调整该车在当前站台的停站时长和下一区间运行等级，使其与前车的追踪间隔尽可能地接近理想追踪间隔。每次列车到站都如此处理，直至列车群达到等间隔行驶效果。

采用前车到站时刻判断法对处于场景(e)的20辆车进行仿真模拟，运行线如图9所示。可以看出，虽然列车之间的追踪间隔逐渐均匀，但效果不好。仿真150 min后，列车之间追踪间隔与理想追踪间隔偏差的最大值仍有4 min。该方法效果不好的原因可能是追踪间隔的计算结果不可靠，如果两车之间有多个站台，且前车在其他站台和区间不是按默认方式行驶，那么该方法计算的追踪间隔和实际追踪间隔存在偏差。此外，该方法未在整体上考虑列车群的相对位置，如果某辆车前方有多辆车堵塞， 且该车与前车的间隔略大于理想间隔，该车将加速往前行驶，不利于堵塞情况的缓解。

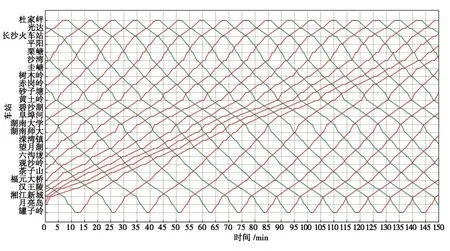
图9 前车到站时刻判断法的仿真运行线Fig. 9 Simulated running line by the judgement method by previous train arrive time

3 结语

针对列车运行紊乱时恢复运营秩序的问题，本文设计了一种等间隔调整方法，其能有效地将列车群调整至等间隔行驶。该方法在整体上考虑了列车的分布情况，并且以最短等间隔调整时长为目标进行了优化处理，弥补了已有方法的不足。

本文所提方法虽然能通过ATS下发调整指令而实现等间隔行车，但无法提前绘制列车计划运行图并对调整过程进行预览。在未来的工作中，需考虑自动生成紊乱状态至等间隔行车状态的计划运行图，使列车按运行图行驶即可实现等间隔行车效果。此外，也需考虑等间隔行驶结束后的调度方法，可设计一种由等间隔运行状态过渡至当天原计划的方法，让列车群恢复至原计划行驶。