基于邻域均匀抽样Bootstrap方法的水泥土无侧限抗压强度演化规律研究

2022-01-09陈昌富陈兆君

地基处理 2021年6期

陈昌富，陈兆君，蔡焕

（湖南大学土木工程学院/建筑安全与节能教育部重点实验室，湖南长沙 410082）

0 引言

水泥土是水泥类胶结材料与土充分拌合后形成的固结体[1]，广泛应用于土木、水利等工程的加固和防渗堵漏。与混凝土和水泥砂浆相比，水泥土的固化过程复杂而缓慢，水泥土的强度在龄期超过28 d后仍然增长明显，只有当龄期超过3个月后，其增长速率才逐渐减缓[1-4]。因此，深入研究水泥土的强度随龄期的变化规律（即演化规律），建立相应的演化方程，对于水泥土加固工程的设计计算和施工进度控制具有重要的理论和工程实际意义。

岩土工程参数测试费时费力，获得的数据样本容量通常较小，极易陷于无法确定总体样本的分布函数和进行较准确的参数估计的困境。20世纪 70年代发展起来的Bootstrap方法[5]（又称为自助法）及其改进方法[6]，可较好地解决上述困境，因为它无需提前假设估计统计量抽样分布形状的概率特征，而且不需要计算抽样分布函数的分析函数便可做统计推断[7]。因此，近年来有学者[8-11]引入Bootstrap方法对小容量样本岩土参数进行统计分析。

本文首先通过大量的文献调研，深度挖掘水泥掺入比在10%～25%之间、龄期在3～90 d范围内的黏性土水泥土无侧限抗压强度（Unconfined Compressive Strength，UCS）试验数据，获得相应的试验数据样本；再通过改进现有的 Bootstrap方法，提出一种新的邻域均匀抽样Bootstrap方法对水泥掺入比分别为10%、15%、20%和25%时水泥土UCS在不同龄期下的均值进行估计；然后采用双曲线型演化模型，对不同水泥掺入比下水泥土UCS均值的演化规律进行回归分析，建立出不同水泥掺入比下黏性土水泥土 UCS的演化方程；最后通过回归分析得到水泥土 UCS演化方程参数随水泥掺入比的变化关系，建立综合水泥掺入比的黏性土水泥土UCS演化方程。

1 基于邻域均匀抽样Bootstrap法的水泥土无侧限抗压强度均值估计方法

Bootstrap方法是按放回抽样方式，相继且独立地从来自总体的原始样本中抽取大量新样本（即自助样本），再通过自助样本对总体进行统计推断的统计方法[5-6]，它实际上是把小样本数据统计问题转化为大样本问题进行分析，可很好地解决小样本试验评估问题。

鉴于传统 Bootstrap法极易产生样本点相同的自助样本，进而导致统计分析结果偏离真实分布[6]，于是本文提出一种新的基于邻域均匀抽样Bootstrap方法，来估计水泥土UCS的均值，具体步骤如下。

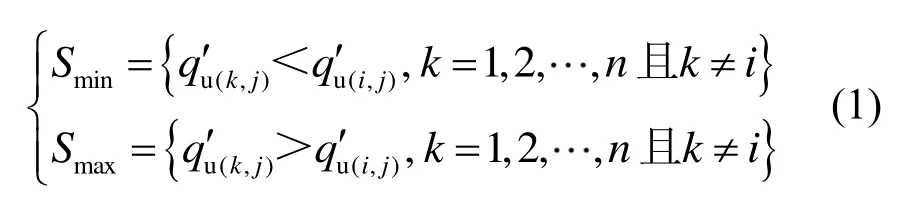
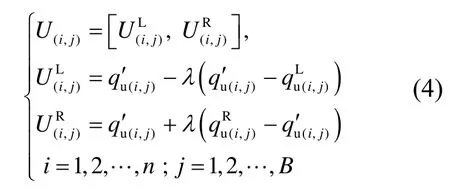
式中：λ为抽样邻域控制参数，由下式确定：

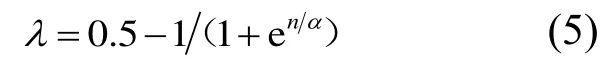
式中：n为原始样本容量；α为λ函数形态调整系数，可取α=2～3，本文取α=2。

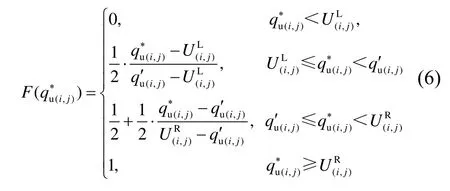
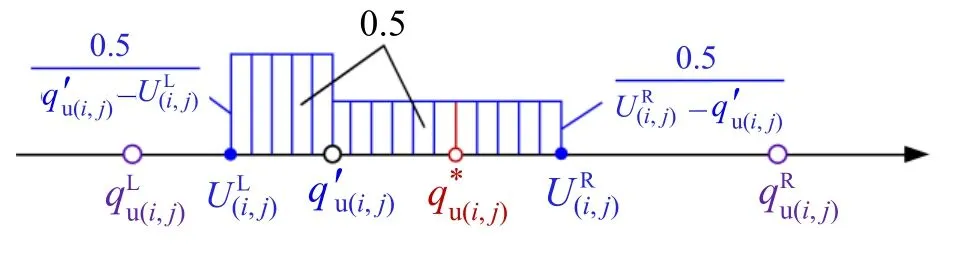
图1 阶梯型概率密度函数Fig. 1 Stepped probability density function

（5）分别求出B个改进自助样本的均值和标准差

2 不同水泥掺入比下水泥土无侧限抗压强度的均值估计

2.1 原始样本数据收集

影响水泥土力学性能的因素有水泥掺入比、龄期，以及水-温-力耦合环境效应等[13]，但最主要的影响因素还是水泥掺入比和龄期。由于工程中常用的水泥掺入比范围为10%～25%[14]，故本文统计了48篇文献[15-62]中水泥掺入比在 10%～25%范围内，龄期在 3～90 d范围内的黏性土水泥土无侧限抗压强度（UCS）试验数据。文中提到的水泥土均为黏性土水泥土，后文不再提及。通过对试验数据整理得到掺入比分别为10%、15%、20%、25%的水泥土在不同龄期下的UCS试验结果散点图，如图2～5所示。

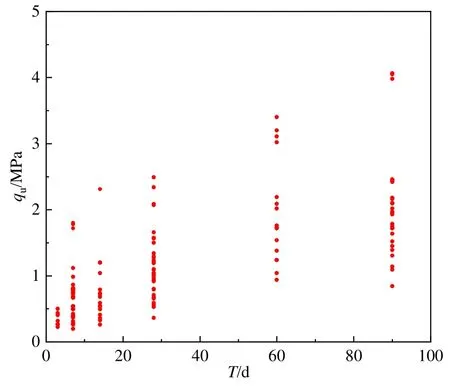
图2 10%水泥掺入比下水泥土UCS散点图Fig. 2 Scatter plot of UCS of cement-soil under 10% cement ratio

图3 15%水泥掺入比下水泥土UCS散点图Fig. 3 Scatter plot of UCS of cement-soil under 15% cement ratio

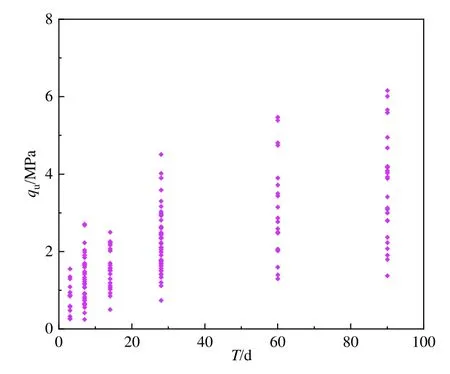
图4 20%水泥掺入比下水泥土UCS散点图Fig. 4 Scatter plot of UCS of cement-soil under 20% cement ratio

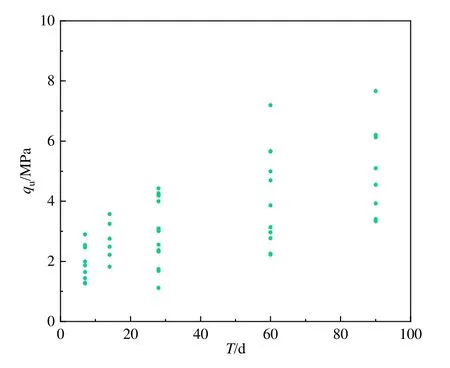
图5 25%水泥掺入比下水泥土UCS散点图Fig. 5 Scatter plot of UCS of cement-soil under 25% cement ratio

2.2 不同水泥掺入比下水泥土无侧限抗压强度（UCS）演化规律

不少国内外学者基于试验结果研究了水泥土UCS演化规律，并提出了相应的演化模型。

按其函数形式大致可分为5种类型（如表1）：

表1 常见的水泥土无侧限抗压强度演化模型Table 1 Common unconfined compressive strength evolution models of cement-soil

指数函数型[15,63]、对数函数型[16-18,49,64-74]、幂函数型[19-24,75-77]、双曲线函数型[25-26,78]和组合函数型[79-80]。其中，双曲函数演化模型形式简单，在原理上能真实地反映全龄期下水泥土UCS的演化规律：即由它计算出的水泥土UCS值在龄期为0 d时为 0，而当龄期趋于无限大时则收敛于一定值。其他演化模型虽然在一定范围内回归效果较好，但在原理上都存在缺陷，比如，对数函数模型在龄期为0 d时水泥土UCS计算值为负无穷大，而幂函数和指数函数模型在龄期趋于无限大时水泥土 UCS计算值却趋向于正无穷大。因此，本文选用双曲线型演化模型来建立水泥土UCS的演化方程。

对收集到的所有原始样本（见图 2～5），采用本文提出的邻域均匀抽样 Bootstrap方法对水泥土UCS的均值进行估计，并基于MATLAB平台编制了相应的计算程序。

为了提高建模精度，将双曲函数模型：

转为下式形式：

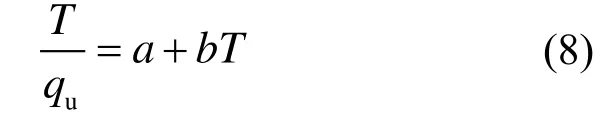
再将每个掺入比下各龄期的水泥土 UCS均值估计值按照式（8）形式整理数据，通过回归分析计算，就可得到T/qu与T的关系式（如图6）及相应的系数a、b值。然后将回归得到的系数a、b值代入式（7），可得到各个单一的水泥掺入比下水泥土无侧限抗压强度（UCS）演化规律（图7）和演化方程（表2）。

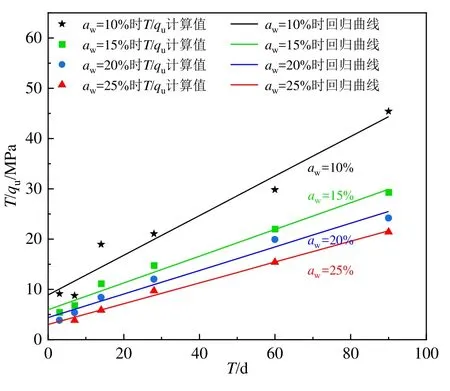
图6 T/qu-T回归曲线Fig. 6 Regression curve of T/qu-T relationship

表2 各单一水泥掺入比下水泥土UCS演化方程Table 2 Evolution equations of UCS of clay cement-soil under each cement ratio

2.3 综合掺入比的水泥土无侧限抗压强度（UCS）演化方程

由图7和表2可知，随着水泥掺入比aw的提高，水泥土无侧限抗压强度的均值增大，而双曲线函数型演化方程中的回归系数a、b则随之减小，如图8和图9所示。

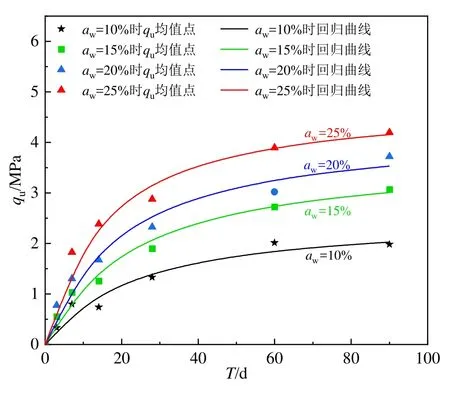
图7 各单一水泥掺入比下水泥土UCS演化规律Fig. 7 Evolution law of UCS of cement-soil under each single cement ratio

采用非线性最小二乘法对各掺入比下演化方程中回归系数a、b与水泥掺入比的关系进行回归分析，得如下回归公式：

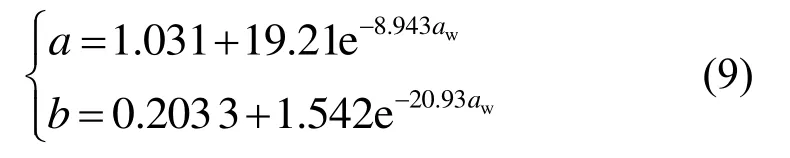
式中：aw为水泥掺入比。

相应的回归曲线如图8和图9所示。

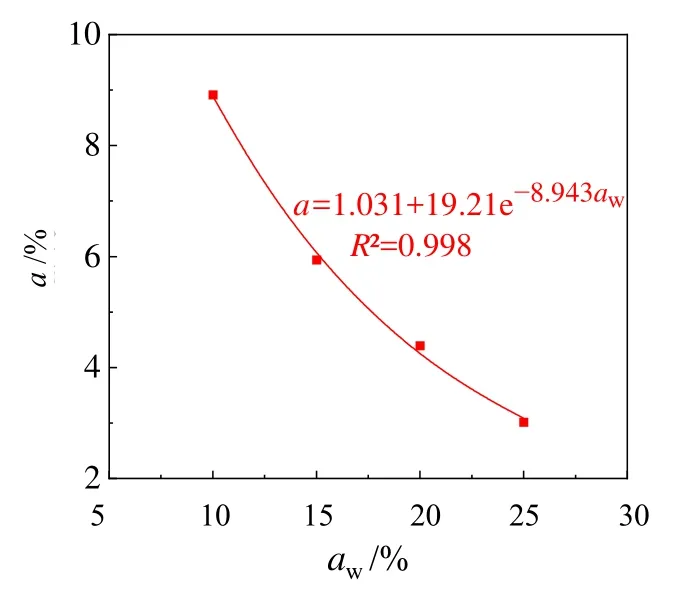
图8 回归系数a与水泥掺入比关系Fig. 8 Fitting curve of relationship between fitting parameter a and cement ratio

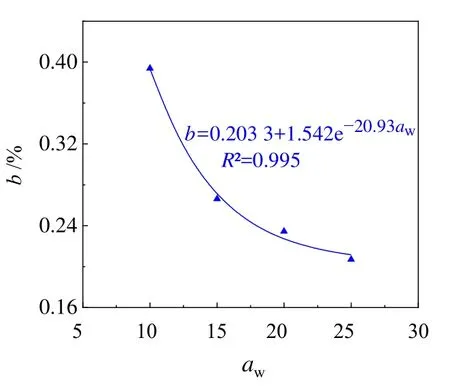
图9 回归系数b与水泥掺入比关系Fig. 9 Fitting curve of relationship between fitting parameter b and cement ratio

将式（9）代入式（7），得到综合水泥掺入比的水泥土无侧限抗压强度（UCS）演化方程为：

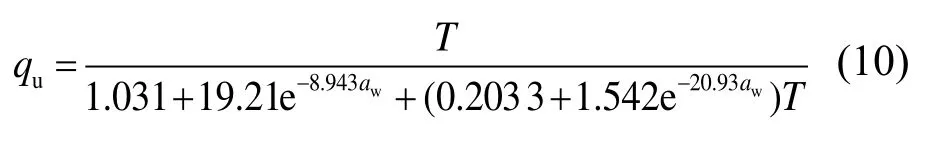
将由式（10）计算出的综合水泥掺入比水泥土UCS演化曲线、各单一水泥掺入比下水泥土 UCS演化曲线和基于邻域均匀抽样 Bootstrap法得出的均值点均绘于图10中，对比分析可以发现，综合水泥掺入比水泥土 UCS演化方程的预测精度高，说明本文建立的演化方程可靠。

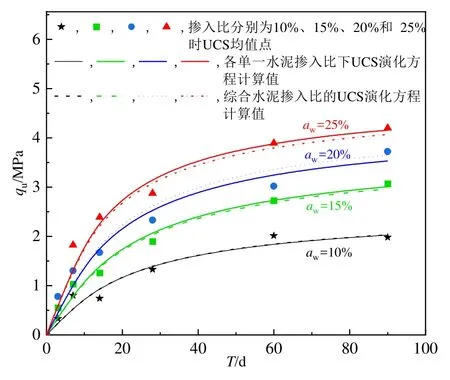
图10 单一和综合水泥掺入比的水泥土UCS演化方程曲线与估计均值点对比Fig. 10 Comparison between UCS evolution equation curve and estimated mean value of clay cement-soil with single and comprehensive cement ratio

根据前文研究结果，并与已有研究结果进行对比分析，可以得出以下结论：

（1）本文基于数据挖掘和非参数Bootstrap方法，回归得到了水泥土无侧限抗压强度（UCS）双曲线型演化方程，并分析确定出方程参数a和b的合理取值范围为：a=3.0～9.0、b=0.2～0.4，当水泥掺入比较大时，a和b取较小值；反之，取较大值。

（2）本文建立的演化方程仅适合于水泥掺入比在10%～25%范围内、龄期在0～90 d范围内的水泥土UCS值的估计。

（3）与其他学者根据各自的试验结果回归得出的演化方程相比，本文收集的试验数据更广泛，数据量更大，因此，本文建立的黏性土水泥土无侧限抗压强度（UCS）演化方程具有更好的适应性。