基于近零指数超材料的频分复用信息传输
2022-01-08周子恒李越
周子恒 李越
(清华大学电子工程系,北京 100084)
引 言
电磁波是信息的基本载体之一. 在信息技术迅猛发展的背景之下,人们需要在空间、频谱、极化等多个物理域对电磁波进行更高精度的调控. 近年来,电磁超构材料[1]迅猛发展,受到了学术界与工业界的广泛关注. 通过设计人工合成的“超原子”及其空间排列,电磁超构材料的等效介电常数和等效磁导率可相应改变,实现天然材料难以具备的电磁本构参数,如单/双负折射率等[1]. 近零指数材料[2]是一种特殊的电磁超构材料,它具有趋近于零的光学折射率,具体可以分为介电常数近零[3](espilon near zero,ENZ)超材料、磁导率近零[4](mu near zero, MNZ)超材料,以及介电常数与磁导率均近零[5](epsilon and mu near zero, EMNZ)超材料. 电磁波在近零指数超材料中具有趋近于无穷的相速度和无限拉伸的波长,因而呈现出独特的空间静态分布而时域震荡的波动效应,即等效的空域-时域解耦效应.
近零指数超材料为调控电磁波提供了全新的自由度. 作为最为新颖的零折射性质之一,近零折射率媒质可以让电磁波无反射地通过形状任意的传输通道,即实现超耦合效应[3,6]. 考虑到波长拉伸带来的大范围相位均匀特性,近零指数超材料可以用于设计多功能透镜[7-8],实现电磁波波前调控. 近零指数媒质内的空间静态场特性也催生了一系列新颖的几何无关电磁功能器件,如空间结构与频率无关的天线[9-11]、几何无关谐振腔[12]、中心枢纽形状任意的功分器等[13],为微波工程和光学工程设计提供了全新机遇.
光学掺杂[14]概念与方法的提出对近零指数超材料发展具有重要意义. 光学掺杂通过在ENZ 背景中加入宏观尺寸的介质光学掺杂异质体,实现对近零指数材料等效磁导率的调控. 具体而言,通过光学掺杂,我们既可实现等效介电常数、磁导率同时近零的EMNZ 材料,亦可等效为磁导率趋近于无穷的理想磁导体(perfect magnetic conductor, PMC)材料. 值得注意的是,光学掺杂效应与ENZ 背景中的光学掺杂异质体的位置、排列方式无关. 光学掺杂的ENZ材料的空间序无关属性与传统的周期性人工电磁媒质有着本质不同,这背后的物理机制是ENZ 背景中的磁场均匀特性使得整块ENZ 区域对电磁波而言等效为一个“点”. 基于光学掺杂的近零指数超材料开启了非周期的、序构无关的人工电磁材料范式,为灵活实现材料在电磁透明与非透明状态之间的切换提供了全新途径.
本文将近零指数超材料引入信息领域应用,提出一种全新的频分复用[15]信息传输实现架构. 首先,我们基于解析理论和数值仿真分析了掺杂近零指数材料的EMNZ 状态与PMC 状态,电磁波在这两种状态上分别呈现出全透射与全反射特性. 通过细致的电磁场分布分析,可以得出光学掺杂异质体在谐振时对近零指数超材料的宏观响应起到关键主导作用.为了对系统传输响应进行有效调制,我们采用金属方环包围光学掺杂异质体,并在环上刻槽且配置开关. 开关受到基带数字信号(0/1)控制,当开关闭合,光学掺杂异质体被屏蔽,超耦合透射峰消失;反之则可以在固定频率上观测到透射峰. 基于此方案,采用多个光学掺杂异质体,可在多个频率上对传输信号进行独立的幅度调制,从而实现频分复用信息传输.我们对该频复用实现架构进行了理论和数值分析,验证了总信道容量随光学掺杂异质体数增加而提升.传统的频分复用方案需振荡器电路来生成载波,需要调制电路对载波进行幅度或相位调制,高频段(如毫米波、太赫兹) 电路损耗较大、成本高昂. 利用ENZ 光学掺杂超耦合效应可直接生成多个载波,无需振荡器电路,且超耦合透射峰的独立可调特性大大降低了开关的复杂度. 由于近零指数超材料可以在微波、太赫兹乃至光学找到实现方案[2],因而该频分复用架构在广阔的频段内具有较好的适用性,尤其在传统集成电路难以胜任的高频段具有潜在优势.
1 掺杂ENZ 材料基本特性
1.1 光学掺杂基本理论
光学掺杂方案将半导体领域的微观元素掺杂方案移植到了光学宏观尺度,其基本概念如图1 左图所示. 考虑一块包含若干介质掺杂异质体的二维ENZ 背景,其介电常数εh≈ 0,总面积为A. 掺杂异质体假设没有磁性,介电常数为εd,面积为Ad(d= 1, 2,3,···). 当外界入射电磁波磁场垂直于纸面时,掺杂的ENZ 材料可以等效为如图1 右图所示的介电常数近零、相对磁导率为μeff的均匀材料. 相对等效磁导率μeff的表达式如下[14]:
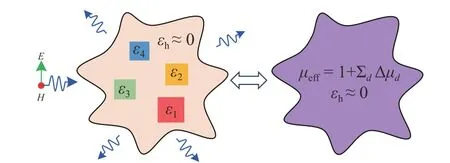
图1 光学掺杂的ENZ 媒质概念图及其等效均匀媒质Fig. 1 The concept plot of doped ENZ medium and the equivalent homogenous medium
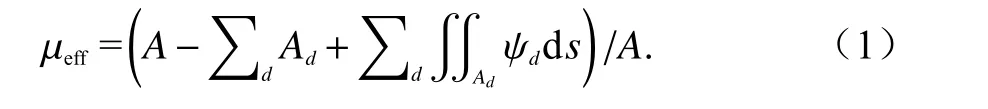
式(1)中ψd代表第d个掺杂异质体中的归一化磁场,服从如下波动方程及边界条件[14]:


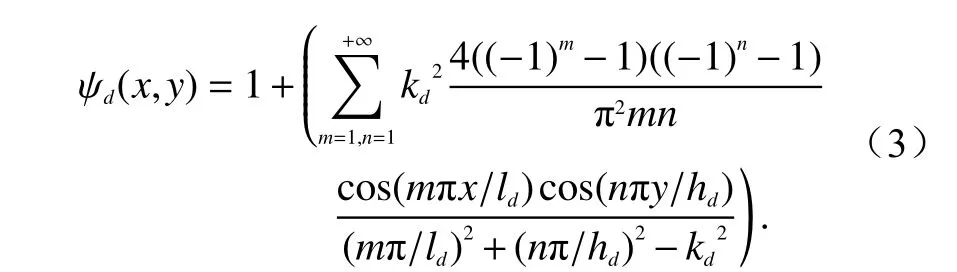
磁场分布表达式(3)的坐标原点设在矩形掺杂异质体的中心,坐标系x轴、y轴分别与矩形的两边平行,求和号里的每一项对应磁壁边界条件下的矩形腔体的TMm,n谐振模式. 考虑ENZ 背景中只包含一个矩形掺杂异质体,将式(3)代入式(1), 可得到掺杂ENZ 材料等效磁导率的具体表达式[16]:
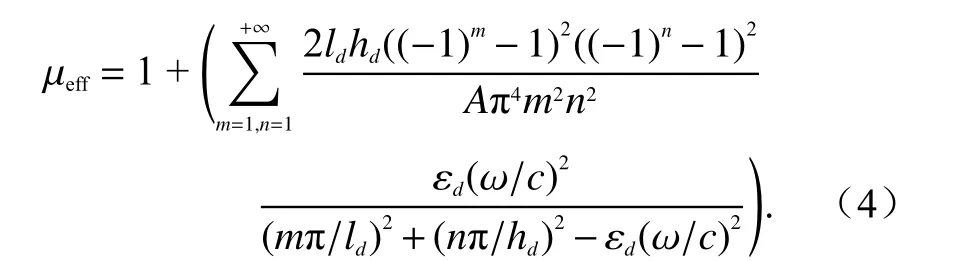
由式(4)可见,矩形谐振腔TMm,n模式的频率即为等效磁导率随频率变化函数的极点. 如果只考察最低阶极点附近的等效磁导率,式(4)求和号中的级数可近似只取第一项,故而化简为
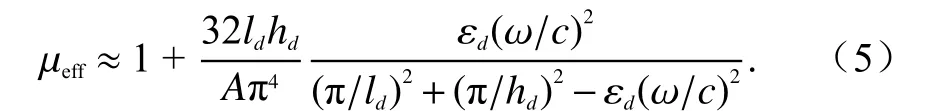
1.2 掺杂ENZ 腔体透射响应分析
本节具体讨论包含单个正方形光学掺杂异质体的ENZ 腔体的传输特性. 如图2(a)所示,考虑一个形状不规则、面积A=563 mm2的二维ENZ 腔体,腔体内掺杂有一个相对介电常数ε1= 40、边长l1=5.6 mm的正方形介质. ENZ 背景的相对介电常数εh由Drude模型描述,即εh(ω) =1-ωp2/(ω2+iωωc),ωp为等离子体频率,取为2π×6.1×109rad/s, 决定介电函数的零点;ωc为等离子体碰撞频率,与介电函数的虚部相关. 掺杂ENZ 腔体与两段空气填充的平板波导相连接,以方便测试透射响应. 入射电磁波为横电磁TEM 模式,磁场极化垂直于纸面. 掺杂ENZ 材料的相对等效磁导率μeff可由式(4)计算可得.μeff随归一化角频率ω/ωp变化的曲线如图2(b) 所示.μeff在ωp处约等于零,掺杂体系呈现出EMNZ 响应;μeff在0.98ωp附近趋近于无穷,呈现出PMC 响应. 由式(5)可知,发生最低阶PMC 响应的频率可由下式确定:

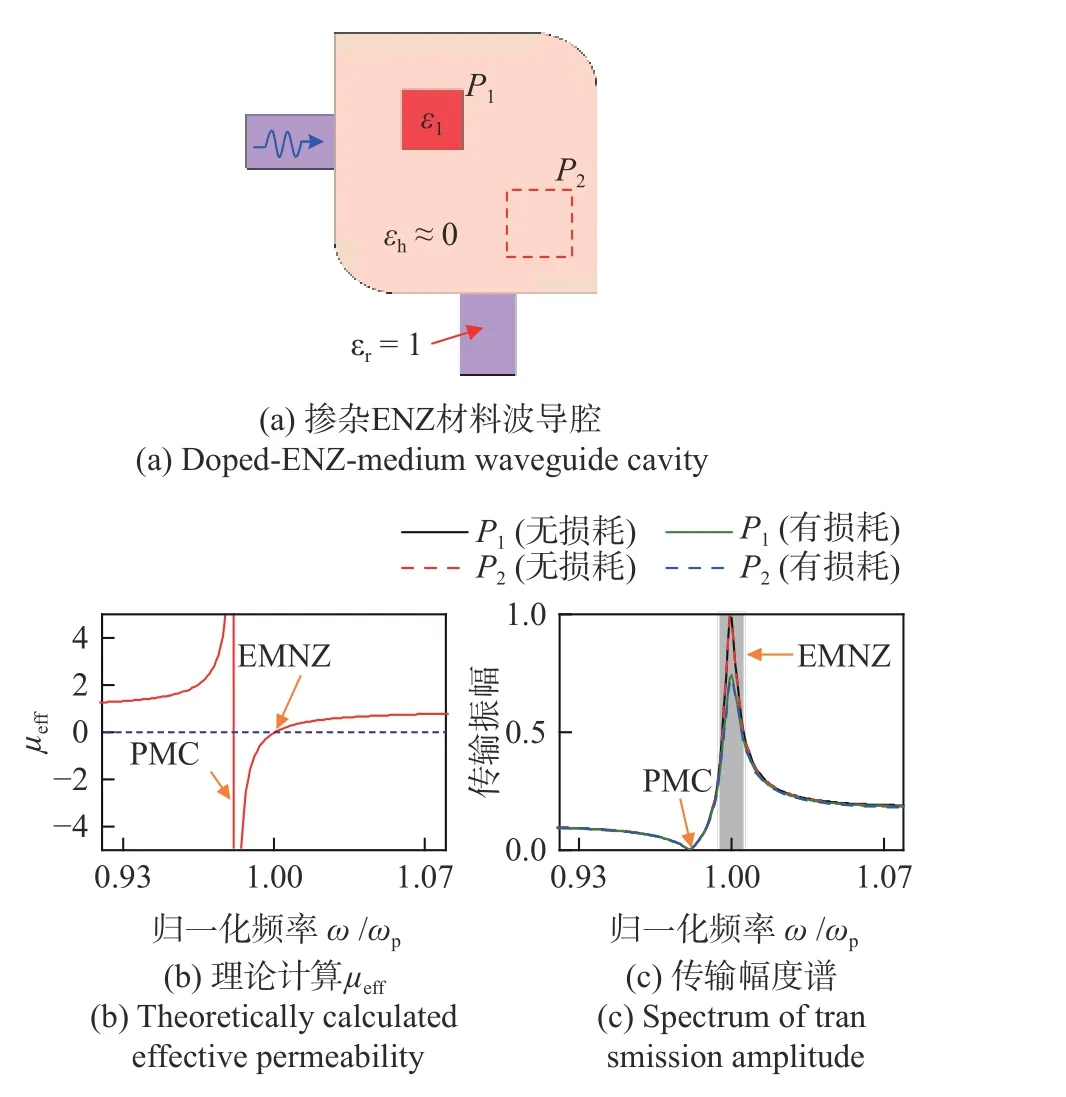
图2 掺杂ENZ 媒质材料μeff 及传输响应Fig. 2 Effective permeability and transmission response of the doped ENZ medium
μeff曲线在ωp附近的强色散特性意味着掺杂ENZ 体系在ωp附近发生磁谐振,我们基于有限元数值仿真软件COMSOL Multiphysics 射频模块对掺杂ENZ 腔体的传输响应进行仿真. 考虑不同的情况:正方形掺杂异质体放置在不同位置P1、P2,以及体系无损耗(ωc=0, ε1损耗正切角为0)与带损耗(ωc=0.01ωp,ε1损耗正切角为0.001),数值仿真得到的传输幅度结果如图2(c) 所示. 在EMNZ 频率上,掺杂ENZ 材料等效磁导率和介电常数同时趋近于零,其特征阻抗得以与外界波导阻抗匹配,因而电磁波可通过不规则腔体,呈现出高传输幅度的透射峰. 在PMC 频率上,掺杂ENZ 材料等效磁导率趋近无穷,特征阻抗亦趋近无穷,因而入射电磁波被全反射,形成传输零点.当掺杂体系带有一定的介质及等离子损耗,EMNZ超耦合传输的幅度将有所下降,但相比于其他频率依然有明显的透射增强效果.
为了直观理解光学掺杂异质体对掺杂体系传输响应的显著影响,我们给出PMC 频率及EMNZ 频率上的电磁场幅度分布图. 在EMNZ 频率上,光学掺杂异质体内的电场在靠近介质边沿的位置达到极大值,而中心的电场较弱,如图3(a)所示;磁场在掺杂异质体中近似为TM11模式,相比于ENZ 背景显著增强,如图3(b) 所示. 值得注意的是,当发生EMNZ超耦合透射谐振时,掺杂ENZ 腔体内的总磁通量为零. 在PMC 频率上,如图3(c)和(d)所示,电磁场同样集中在光学掺杂异质体内. 但由于此时ENZ 背景中的磁场为零,透射电磁波幅度为零. 由于体系电磁能量显著集中于光学掺杂异质体中,ENZ 超材料的整体透射响应受到掺杂异质体高度调控.

图3 掺杂ENZ 媒质腔体电磁场幅度分布Fig. 3 Electric field and magnetic field distribution over the doped ENZ cavity
2 ENZ 超材料频分复用架构
由第1 节理论分析可得,光学掺杂异质体对ENZ 材料的透射响应调控有主导作用,因而只要对掺杂异质体加以设计,即可实现对系统传输响应的高效调制. 本节将通过多个加载开关的掺杂异质体对处于不同频率的EMNZ 超耦合透射峰进行独立调制,从而形成多个独立的信息传输通道,实现频分复用. 所设计的新型频分复用实现架构如图4 所示,主体结构采用包含多个掺杂异质体D1、D2、D3的ENZ 腔体. ENZ 背景面积为 60×25 mm2,相对介电常数由Drude 模型来描述,等离子体谐振频率ωp取为2π×6.1×109rad/s. 三个正方形光学掺杂异质体的介电常数均为40,边长分别为6 mm、5.6 mm、5.2 mm. 多掺杂ENZ 腔体与两段空气填充的波导相连,左侧波导的入射信号为一宽带信号,入射电磁波磁场极化垂直于纸面. 为了在多个频率对信号进行独立调制,实现多载波同时传输,我们在每个掺杂异质体外围包裹方形金属环壁,并在金属环上刻蚀宽度为1 mm的槽. 进而,在槽上加载开关S1、S2、S3,控制金属开口环是否形成闭环. 开关受到带调制的基带数字信号的控制,当需要发送的信息比特为“1”,开关处于断开状态,即“1”状态. 由于磁场与金属壁平行,此状态下光学掺杂异质体可以被正常激励,产生超耦合透射峰,即在对应频率生成载波. 当需要发送的信息比特为“0”,开关处于闭合状态,即“0”状态. 此时光学掺杂异质体被闭合的金属环壁完全屏蔽,超耦合透射峰消失,对应频率的载波幅度几乎为0. 掺杂异质体的开关控制电路如图4(b)所示,包括PIN 管、隔直电容以及阻交电感. PIN 管导通与否由偏置信号即基带符号决定,其在微波波段的响应时间约为400 ns. 多个可重构的光学掺杂异质体可对频率位于ω1,ω2,ω3的载波幅度进行独立调制. 例如,如图4 所示,当开关S1、S2、S3的状态为“1”、“0”、“1”,预期生成的多载波信号如右侧波导输出信号所示.

图4 基于掺杂ENZ 腔体的频分复用架构Fig. 4 Architecture of FDM scheme based on the doped ENZ cavity
基于电磁数值仿真对多载波独立幅度调制方案进行验证. 当需要发送的三个信息比特为“0”、“0”、“0”,所有开关均处于闭合状态,所有载波均处于低传输幅度状态,传输系数频谱如图5(a)所示.当需要发送的三个信息比特为“0”、“1”、“0”,开关S1、S2、S3分别处于闭合、断开、闭合状态,传输频谱如图5(b)所示,只有频率处于ω2的载波处于高传输幅度状态. 当需要传输的三个信息比特为“1”、“0”、“1”,所生成的载波频谱如图5(c)所示,频率处于ω1和ω3处的载波处于高传输幅度状态. 当所有开关均断开,传输信息比特为“1”、“1”、“1”,所形成的载波频谱如图5(d)所示,此时频率处于ω1、ω2、ω3的载波均处于高传输幅度状态. 由于ENZ 媒质的色散特性,远离等离子谐振频率ωp处的超耦合传输峰的透射率会略微下降,但透射峰值基本维持在0.9 以上. 为验证载波传输体系工作在EMNZ 超耦合状态,给出了可重构多掺杂体系内的磁场幅度分布.如图6(a) 和(b) 所示,开关S1、S2、S3分别处于“断开”、“闭合”、“断开”状态,即传输比特为“1”、“0”、“1”时,体系在频率ω1、ω3上处于EMNZ 超耦合状态. 同时,由于开关S2闭合,掺杂异质体D2内的磁场严格为零,ω2处的传输峰无法被激励.
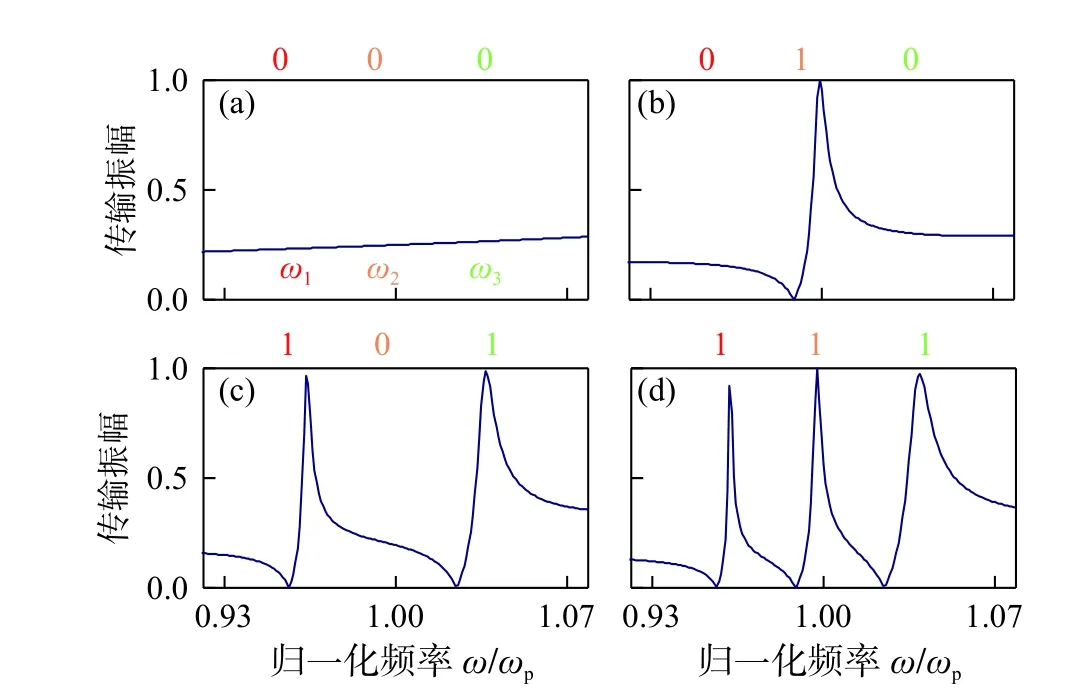
图5 掺杂异质体开关处于不同状态时的系统传输谱Fig. 5 System transmission spectrum for the switches of dopant at different states

图6 基于掺杂ENZ 腔体的频分复用结构中的磁场分布Fig. 6 Magnetic field distribution over the FDM structure based on the doped ENZ cavity
频分复用传输的关键在于将多个串行传输的信息比特转化为并行的信息比特,同时调制于不同频率的子载波上,从而成倍地提升信道容量. 基于ENZ超材料,包含q个光学掺杂异质体(即q个载波)的频分复用架构的信道容量可由香农公式[17]计算:

式中:Δfd表示第d个光学掺杂异质体对应的超耦合传输峰的3 dB 带宽,对应第d频率通道的带宽;RSN表示信噪比;|Sd,21| 表示第d个超耦合传输峰的振幅,可通过电磁数值仿真提取. 基于掺杂ENZ 媒质的频分复用架构的信道容量随信噪比变化规律如图7(a) 所示,这里考虑加入1 个与3 个光学掺杂异质体情况(即1 通道与3 通道情况),还考虑了ENZ体系无损耗(ωc= 0)与有损耗(ωc= 0.5%ωp)情况. 所计算的信道容量对单通道传输带宽进行了归一化,由图7(a)可见,在多光学掺杂异质体情况下,系统信道容量相对于单光学掺杂异质体情况有明显提升,且该提升值在高信噪比区域更加明显. 我们还给出了信道容量随光学掺杂异质体数量,即频谱通道数的变化关系,如图7(b)所示. 由图7(b)可见,在无损耗条件下,频分复用系统信道容量随着掺杂异质体数量近似线性增加;当ENZ 体系存在等离子体损耗,信道容量提升在掺杂异质体数量较大区域有所减缓.
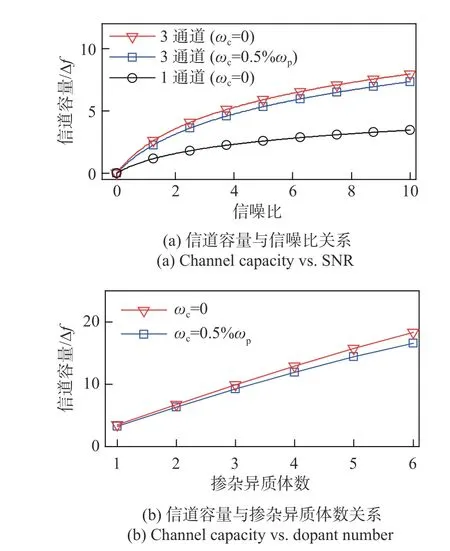
图7 基于ENZ 腔体的频分复用系统的信道容量随信噪比、掺杂异质体数的变化Fig. 7 Variation of the channel capacity of the FDM system based on the doped ENZ cavity with SNR and number of dopants
我们以两种光学掺杂物为例讨论子载波的带宽问题,如图8 所示. 两种光学掺杂物情况如下:光学掺杂物相对介电常数εd选为20,两个正方形光学掺杂异质体的边长分别为0.176λp及0.156λp(λp为频率ωp时的自由空间波长); 光学掺杂物相对介电常数εd选为80,两个正方形光学掺杂异质体的边长分别为0.085λp及0.076λp. 由全波仿真得出的传输谱可见:采用低介电常数、大尺寸的掺杂介质体可以提升载波带宽;此外,提升EMNZ 超耦合的工作频率可以提升载波的绝对带宽. 由于从红外到光学波段可找到损耗较低的等离子材料,光学波段的ENZ 材料有透明金属氧化物(ITO 等),红外波段的ENZ 材料有SiC 等半导体材料[18],而ENZ 超材料更是在微波乃至光学频带均可以找到合适的实现方式[17],且光学掺杂在实际光学材料中的可行性也已得到验证[14,19],因此,所提出的频分复用物理实现架构原则上可以应用于广阔的频段.
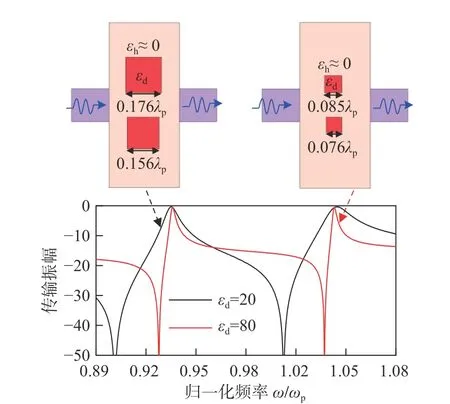
图8 两种光学掺杂物的载波带宽Fig. 8 Bandwidth of 2 photonic doping carriers
3 结 论
本文深入讨论了光学掺杂对ENZ 超材料传输特性的影响机理,进而基于可重构的光学掺杂效应提出了一种频分复用信息传输的新型实现架构. 通过对光学掺杂异质体包裹金属环壁并加载开关,即可对分布在不同频率上的超耦合透射峰进行独立幅度调制,从而同时传输多路信息,显著提升信道容量.由于ENZ 材料具有几何无关特性和光学掺杂异质体位置任意的特点,本文提出的频分复用实现架构具有高实现灵活性、结构紧凑等优势,而且能够适用于微波、毫米波乃至更高的频率. 未来可基于该方案和思路搭建实际的高频信息传输模块.
