基于编码电磁超表面的Bessel 波束设计

冯强 林屹峰 单明明 李龙

（1. 西安电子科技大学 超高速电路设计与电磁兼容教育部重点实验室，西安 710071；2. 人工智能与数字经济广东省实验室 智能超材料中心，广州 510330）

引 言

电磁超材料理论和技术的发展从最初的等效媒质理论设计发展到现在的信息超材料[1-9]，经历了从模拟时代到数字时代的转变[3]. 从最初基于等效媒质理论进行的单负(介电常数为负或磁导率为负)和双负(介电常数和磁导率均为负)材料设计[1-2]，然后又经历了编码超材料、数字超材料和基于数字可编程器件的可编程超材料[4-5,10]，之后电磁超材料又进一步结合了信息科学中的信息论和智能调控算法[11-13].目前电磁超材料的概念和理论已延伸至信息超材料[6-9].

电磁超表面是电磁超材料的一种二维实现形式，而目前大多数的电磁超材料对于电磁波的调控是通过电磁超表面的形式来实现的[6,14]. 鉴于电磁超表面对于电磁波的灵活调控能力，其可以用于Bessel波束的产生与调控设计[15-22]. Bessel 波束最早是由Durnin J. 在1987 年提出的，它是满足波动方程在自由空间中的一个解[23-24]. 早期关于Bessel 波束的研究主要在光学领域，后来逐渐发展到了电磁领域[25-26]，而Bessel 波束在近场探测成像[27-29]以及近场无线功率/信息传输等方面均有重要应用[17,30-33].

本文以编码电磁超材料作为切入点，基于编码电磁超表面的设计理论与设计方法，为Bessel 波束的数字化产生与调控提供新的设计思路. 同时，Bessel波束在面向信息超材料平台/系统开展有关的应用研究时，也可以进一步促进其在雷达探测与成像以及无线通信等领域中的应用. 文献[34] 中构建的可编程编码超表面平台，在进行轨道角动量(orbital angular momentum, OAM)涡旋波通信传输实验时就采用了涡旋波束聚焦的设计方法以提高平台的通信性能. 由于都是采用了数字化编码设计方案，基于编码电磁超表面的Bessel-OAM 波束设计方案也可以较为直接地应用到该可编程超表面平台上来进行具有波束汇聚能力的Bessel-OAM 涡旋波束传输与设计，以起到提升涡旋波束通信传输性能的作用.

本文的主要内容如下：首先对Bessel 波束的基本理论和设计方法进行介绍，并以反射型人工电磁表面产生Bessel 波束的设计为例进行较为详细的举例说明. 接着，设计了一款反射型电磁超表面单元并对其进行编码设计，以用于能够产生Bessel 波束的编码电磁超表面设计，并给出了典型的反射型电磁超表面的全波电磁仿真模型. 然后基于基本的Bessel波束设计理论和构建的编码电磁超表面模型分别设计产生了多种不同类型的Bessel 波束，包括单波束零阶Bessel 波束、双波束零阶Bessel 波束、单波束高阶Bessel 波束以及双波束高阶Bessel 波束. 在设计实现这些不同类型Bessel 波束的同时，分别给出对应有关波束的具体设计方法和与之相对应的波束仿真结果. 最后是本文的总结部分.

1 Bessel 波束基本理论

首先，我们从最基本的波动方程出发来探讨Bessel 波束的基本理论[23-24,35]. 在柱坐标系中，自由空间中电场的波动方程可以表示如下：

式(2)对应波动方程的解是在没有任何边界条件约束下所对应的波动方程的一个解，而实际的电磁波辐射问题还需要考虑到其中的一个边界条件，即索末菲尔德辐射边界条件(Sommerfeld radiation condition)[35]，然后通过分离变量法，可以得到对应于波动方程(1)的一个解，形式如下[35]：

式中，Eout(r,φ,z)、Ein(r,φ,z)分别表示关于柱坐标系中Z轴的外行和内行锥形波束，当内行锥形波束经过坐标系Z轴后便转换为对应的外行锥形波束. 两种波束交汇的坐标系Z轴附近，二者进行叠加之后便形成了式(4)中的Bessel 波束，由于其只在有限的区域内保持，故将其称为准Bessel 波束，并非严格意义上的理想Bessel 波束. 详尽的推导和解释可以参考文献[35].

以反射型电磁超表面模型为例，对上述产生Bessel波束的基本原理与方法作进一步介绍. 图1 所示为一个经由反射型电磁超表面产生偏转的Bessel 波束原理示意图，uˆ0表示波束偏转指向. 经由电磁超表面调控之后的内行锥形电磁波束经过坐标系的Z′轴之后变成外行的锥形波束，而内行的锥形波束和外行的锥形波束在Z′轴附近交汇叠加形成了相应的Bessel 波束区域. 其中，tan α=kr/kz， α表示对应锥形波束的锥角大小. 这一电磁波束调控过程构成了产生Bessel 波束的基本原理.

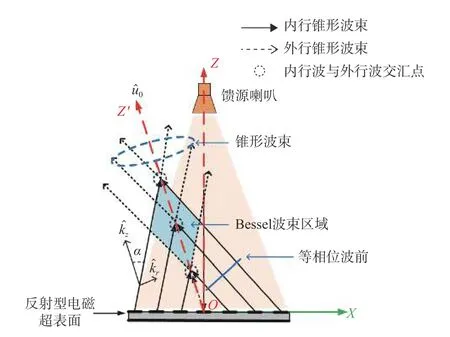
图1 基于反射型电磁超表面产生Bessel 波束的原理示意图Fig. 1 Schematic diagram of the reflective metasurface for Bessel beams generation

2 Bessel 波束产生设计

基于第1 节的Bessel 波束基本理论，以反射型编码电磁超表面为模型，分别对不同形式的Bessel波束进行设计和仿真实现. 先给出Bessel 波束设计时所采用的反射型电磁超表面单元及其有关的仿真参数与电磁响应特性，以及反射型电磁表面模型；然后针对不同类型Bessel 波束设计给出具体与之相对应的设计方法以及仿真结果，并作简要分析.

2.1 反射型编码电磁超表面设计

本小节主要对反射型编码电磁超表面的单元形式与设计参数、电磁超表面单元的电磁响应特性、反射型编码电磁超表面的编码方式以及超表面的阵列形式等有关设计方案与设计参数进行介绍.

2.1.1 反射型编码电磁超表面单元设计

对于反射型编码电磁超表面的单元设计形式，选取经典的“耶路撒冷(Jerusalem)”方环结构[36]. 图2所示为我们设计的反射型电磁超表面单元结构形式，表1 为该单元结构的具体设计参数，中心工作频率为10 GHz. 编码电磁超表面主要通过对超表面单元进行离散比特化设计来实现.

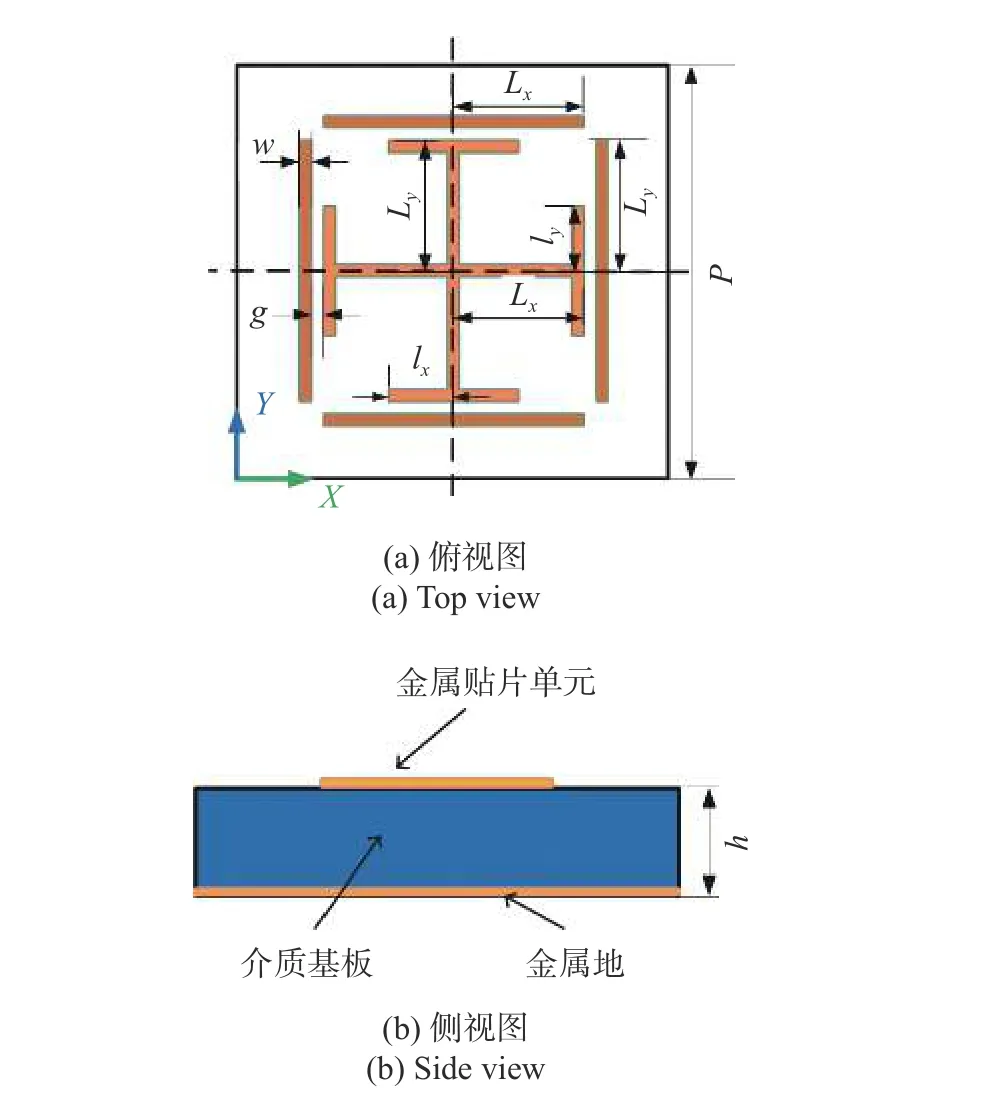
图2 反射型电磁超表面单元结构示意图Fig. 2 Geometry structure diagram of the designed reflective metasurface unit cell

表1 反射型电磁超表面单元结构参数Tab. 1 Geometry structure parameters of the designed reflective metasurface unit cellmm

图3 为反射型电磁超表面单元的反射相位特性及相应的超表面单元编码状态选取示意图. 可以看出，通过改变超表面单元的长度参数Ly，可以实现超表面单元从0°～360°的任意反射相位响应. 编码超表面进行编码设计的基本思路为：通过选取超表面单元的特定几个反射相位状态响应来进行超表面阵列的编码设计，而不是选取连续的相位变化状态；通过对电磁超表面的离散化和比特化设计，结合PIN二极管加载和后端的数字电路控制，便可以方便地实现电磁超表面的可编程设计和数字化设计[4,37-38].

图3 反射型电磁超表面单元的反射相位随单元尺寸Ly 变化曲线及编码状态选取Fig. 3 Reflection phase curve vs. the length of the reflective metasurface unit cell, and the schematic diagram of the coding statements

从图3 连续变化的相位曲线中选取4 种不同的状态来实现超表面单元的2 比特编码设计，分别选取超表面单元反射相位为 0°、-90°、180°和+90°这4 种离散状态作为“00”、“01”、“10”和“11”这4 种不同的编码状态. 在后续的编码电磁超表面阵列设计过程中，采用这4 种编码状态的超表面单元进行有关Bessel 波束的产生与调控设计.

为进一步说明电磁超表面单元的电磁响应特性，图4 给出了反射型电磁超表面单元反射幅度特性随单元尺寸参数Ly的变化曲线. 可以看出，该反射型超表面单元具有良好的反射特性，在设计的变化尺寸范围内该单元基本可以保持大于-0.15 dB 的反射效果，在实际阵列设计过程中近似认为其与全反射的效果等同.

图4 反射型电磁超表面单元的反射幅度随单元尺寸Ly 变化曲线Fig. 4 Reflection amplitude curve vs. the length of the reflective metasurface unit cell

2.1.2 反射型编码电磁超表面阵列设计

编码电磁超表面阵列的设计与连续型电磁超表面的设计以及传统反射阵列天线的设计流程基本一致. 相比于传统连续型电磁超表面的设计，在计算得到编码超表面口径面所需的口径场相位分布之后，还需对该口径场相位分布进行离散化处理，即需要将口径面上的相位分布值近似地对应到相应超表面单元的离散状态所具有的那个相位值.

图5 所示为一个典型的单馈源反射型电磁超表面设计模型. 其中馈源喇叭的位置为(fx,fy,fz)，超表面产生的其中一个波束指向为uˆ0=(θ0,φ0). 将超表面上任意位置处的超表面单元所在位置记为(xmn,ymn)，m和n分别表示超表面单元位于超表面阵列的行数和列数.

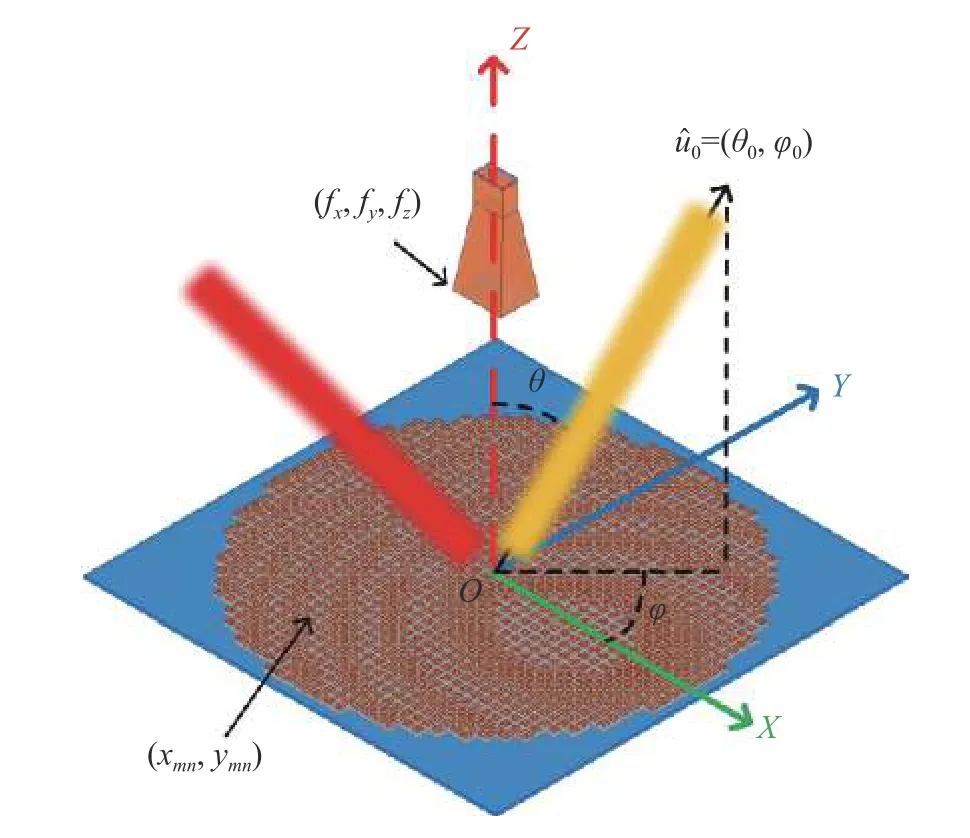
图5 单馈源反射型电磁超表面设计仿真模型Fig. 5 Simulation model of the designed single feed reflective metasurface

超表面阵列的设计关键在于对波束在超表面阵列口径上所需要的口径场相位分布的计算. 下面以零阶单波束Bessel 波束的设计过程为例进行说明.反射型电磁超表面阵列口径面上的切向电场分布可以表示为

式中：k表示对应的波数；dmn表示馈源喇叭的相位中心和(xmn,ymn)位置处超表面单元的距离； λ表示波长；α对应于图1 中用于产生Bessel 波束的锥角大小. 由此，根据方程式(5)～(8)便可以由具体要设计的波束计算得到相应的口径面相位分布，进而实现电磁超表面的波束调控功能设计. 一般对于反射型电磁超表面的设计，对应各超表面单元的幅度响应是相同的，即对A(xmn,ymn)这一项取常数值.

对零阶Bessel 波束的设计，需先对反射型编码电磁超表面有关的参数进行确定. 馈源喇叭口面到超表面的距离为(fx,fy,fz) = (0, 0, 300) mm，超表面的阵列规模为40×40，对应选取一个半径为200 mm 的圆形区域作为实际设计的超表面区域，它也同时对应着20 个超表面阵元的排布数量. 整体超表面阵列大小为420 mm×420 mm，超表面所采用的介质基板类型是相对介电常数为 εr=2.65 的F4B、厚度为3 mm.单波束零阶Bessel 波束指向uˆ0=(θ0,φ0) = (30°，0°)，圆锥角α=10°.

根据以上参数及方程式(5)～(8)对该超表面设计所需要的口径场补偿相位分布进行计算，如图6所示. 图6(a)为连续型口径相位分布，编码超表面设计的关键步骤在于对连续型相位的离散化和状态编码；而图6(b) 为对应于图6(a) 且经过2 比特离散量化之后的编码相位分布，4 种不同的相位状态0°、-90°、180°以及+90°分别对应“00”、“01”、“10”和“11”这4 种不同的编码状态. 基于图6(b)中的离散相位分布及其与图3 中编码超表面单元的对应关系，可以对应得到图7 所示的反射型编码电磁超表面阵列设计及其对应模型.

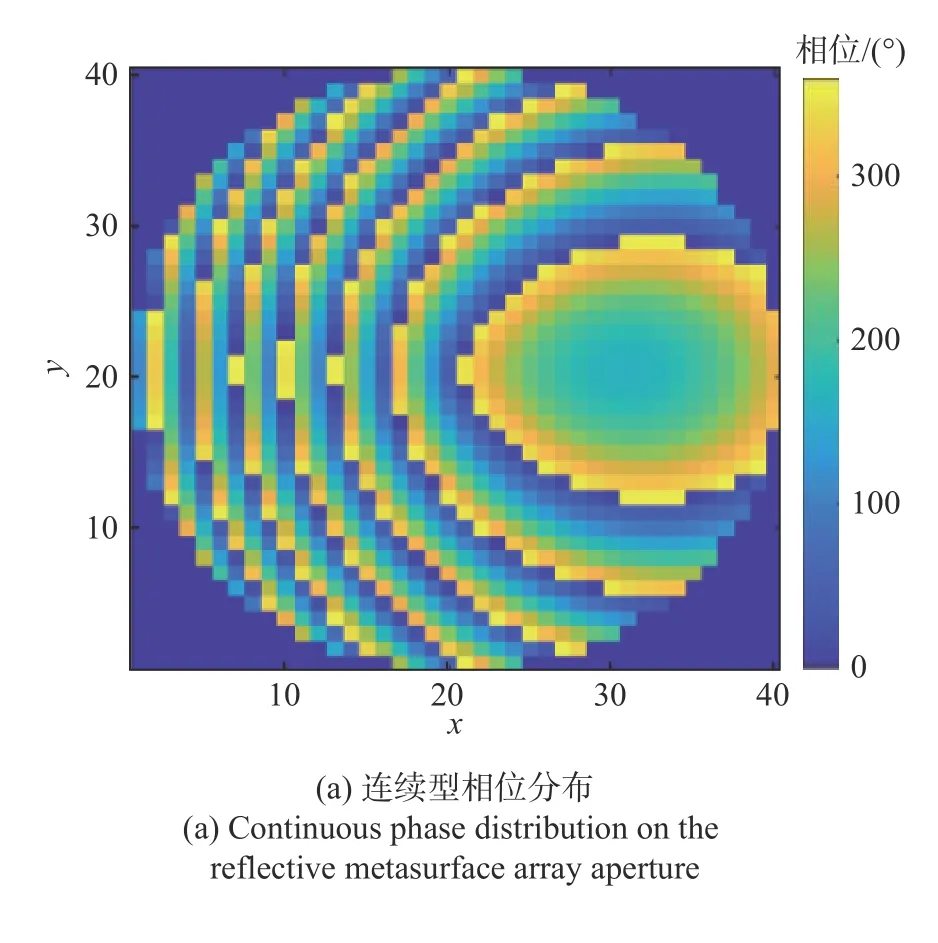
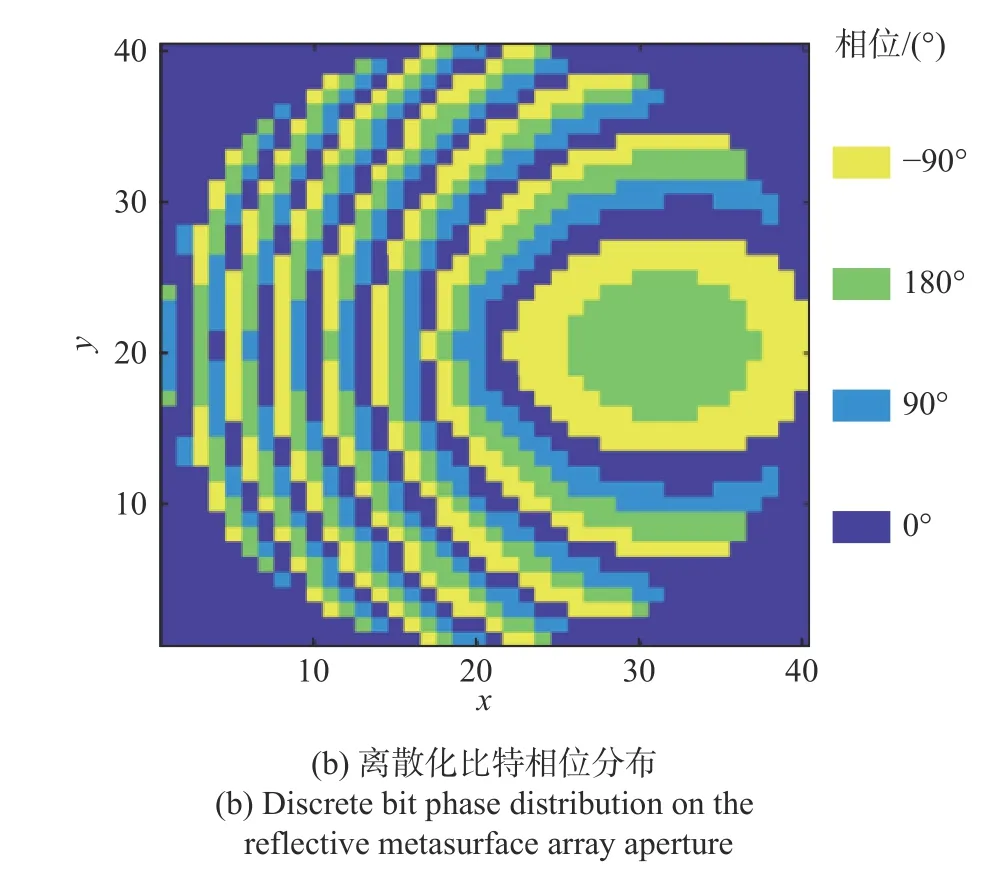
图6 反射型电磁超表面口径相位分布Fig. 6 Phase distributions on the reflective metasurface array aperture

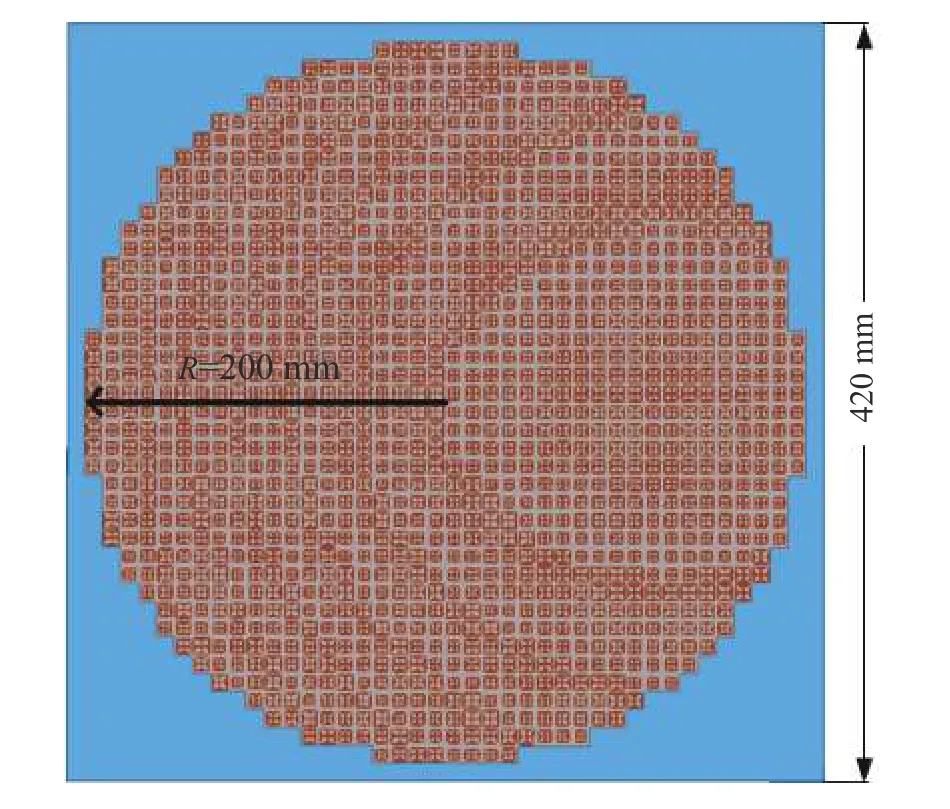
图7 反射型编码电磁超表面阵列模型Fig. 7 Layout model of the designed reflective coding metasurface

以上即是编码电磁超表面的基本设计过程. 在文章的后续部分，基于此设计过程分别对不同类型的Bessel 波束进行设计和仿真，且主要给出对应不同类型Bessel 波束的产生设计方法以及对应得到的仿真结果，而与之相对应的中间设计过程将不再详述.

2.2 不同类型Bessel 波束设计与仿真

首先对零阶Bessel 波束分别进行单波束和多波束的设计，并给出与之对应的仿真结果；然后对高阶Bessel 波束进行设计仿真，并给出不同阶Bessel波束的单波束和多波束设计方法. 对高阶Bessel 波束来讲，其自身具有OAM 特性[18,20,35,39-41]，而Bessel波束自身的阶数也与相应的OAM 模态阶数对应，在对应的设计部分将进行详细介绍.

2.2.1 单波束零阶Bessel 波束设计与仿真

基于2.1 节中对单波束零阶Bessel 波束设计所得到的反射型编码电磁超表面电磁仿真模型，通过电磁仿真计算得到其所对应的空间电场分布结果，如图8 所示. 图8(a)中，Z′轴对应于偏转的Bessel 波束传播轴，场观察面与波束传播轴垂直，且位于Z′=600 mm 处. 图8(b)为与Bessel 波束传播轴平行的轴截面内的电场强度分布仿真结果. 可以看出，反射型编码电磁超表面设计确实产生了预期的偏转零阶Bessel 波束，说明了设计方案的有效性.

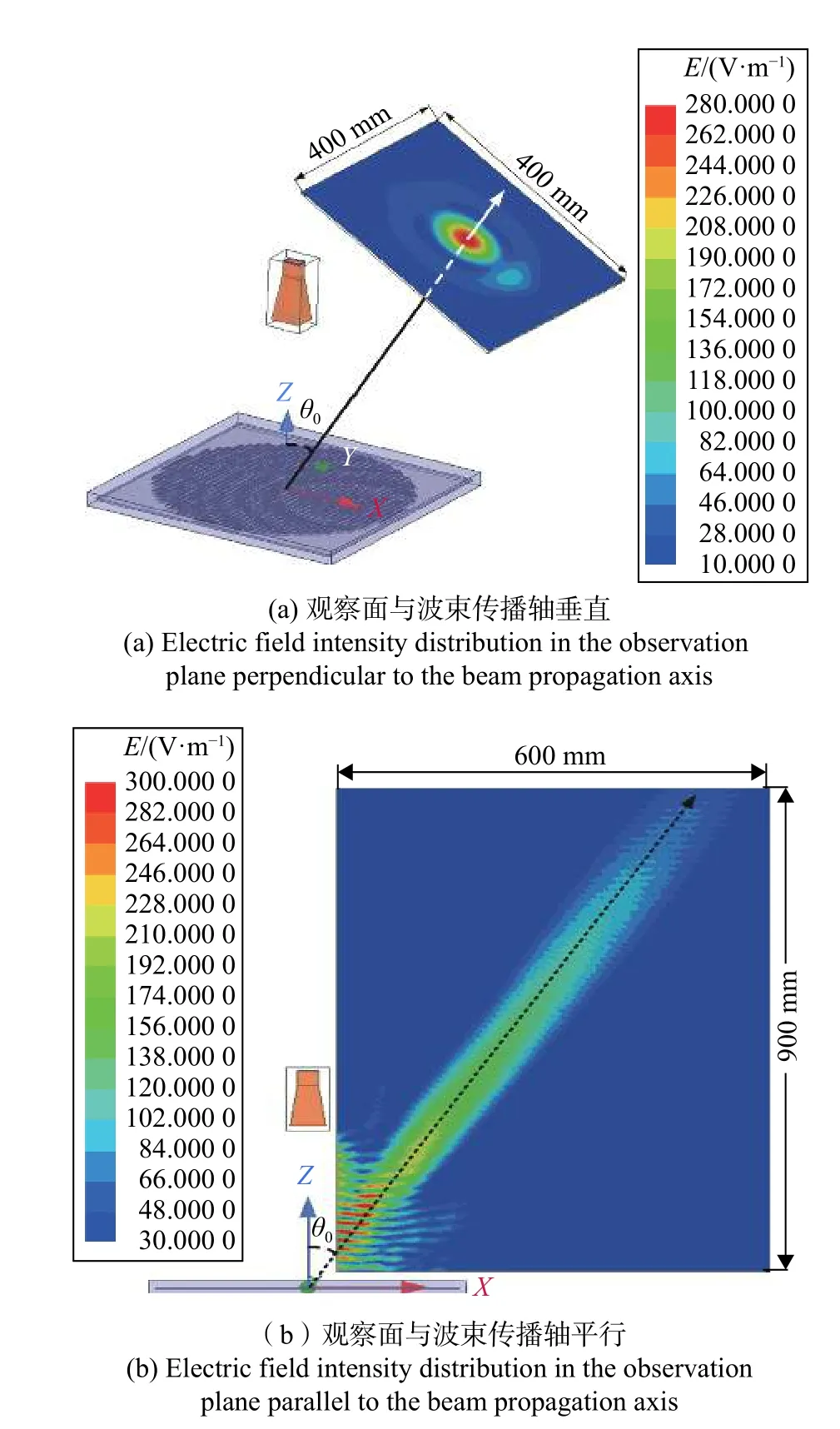
图8 单波束零阶Bessel 波束在观察面内的电场强度分布Fig. 8 Electric field intensity distribution of the single beam Bessel beam of the zero order in the observation plane

2.2.2 双波束零阶Bessel 波束设计与仿真

基于2.1 节中的方程式(5)，多波束零阶Bessel波束对应的反射型电磁超表面阵列口径面上的切向电场分布可以表示为

双波束零阶Bessel 波束两个波束指向分别为uˆ1=(θ1,φ1)=(30°，0°)和uˆ2=(θ2,φ2) =(-30°，0°). 图9 为双波束零阶Bessel 波束仿真模型和对应的空间电场仿真观察面设置及观察面内的电场分布仿真结果.观察面的大小和位置参数与图8 中均相同，后边所有仿真模型的场观察面的参数设置也均与此相同.

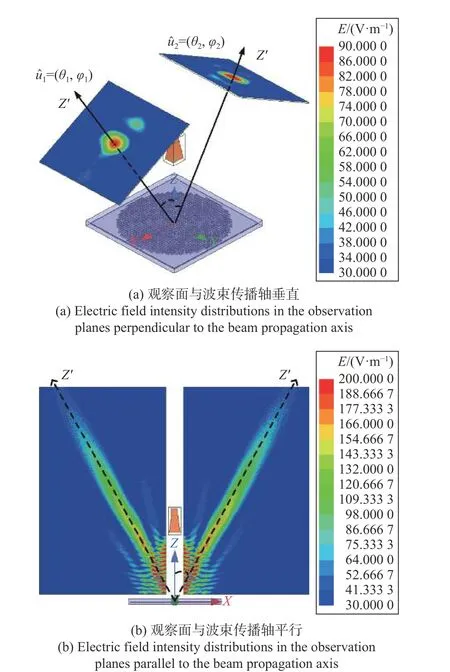
图9 双波束零阶Bessel 波束在观察面内的电场强度分布Fig. 9 Electric field intensity distributions of the dual beams Bessel beam of the zero order in the observation planes

2.2.3 单/双波束高阶Bessel 波束设计与仿真

零阶Bessel 波束对应于方程式(4) 中的ℓ = 0，而高阶Bessel 波束对应的ℓ取值为非零整数，因此高阶Bessel 波束的电场表达式中比零阶Bessel 波束多了exp(jℓφ)，与电磁波的OAM 相对应[39,41]，说明高阶Bessel 波束本身就具有OAM 属性. 同时，鉴于电磁超表面具有的对于涡旋电磁波束的产生与调控能力[42-45]，基于反射型编码电磁超表面对高阶Bessel 涡旋波束进行设计，并对其OAM 涡旋场分布进行分析.

用于产生高阶Bessel 波束所需要的超表面口径相位分布计算公式为

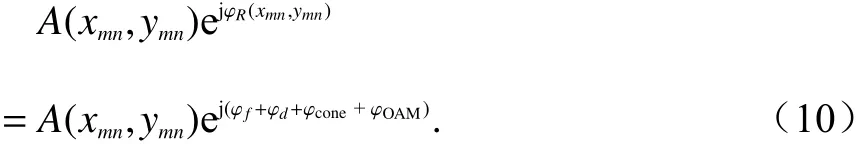
相比于式(5)，式(10)中对于口径场相位分布的计算增加了φOAM这一项，φOAM=arg{exp(jℓφ)}，产生对应的OAM，对应的阶数ℓ即高阶Bessel 波束的阶数，通过式(10)即可实现单波束高阶Bessel 波束的设计.多波束高阶Bessel 波束的设计参照式(9)，可以写成如下形式：

式中：i表示不同的波束类型；φf,i、φd,i、φcone,i、φOAM,i分别对应不同类型波束的具体参数设置. 口径场幅度项A(xmn,ymn)同样近似为等幅均匀分布，这样的近似处理会给设计尤其是多波束的设计引入误差. 其虽可以通过一些阵列优化设计的方法进行较为准确的设计[46]，但一般在进行原理方法验证和说明的设计中不作为主要矛盾，因此通过等幅度均匀分布的近似处理可以带来设计上的简便.

图10 和图11 分别为建模仿真得到的单波束2 阶Bessel 波束在对应的场观察平面内的电场分布仿真结果，波束偏转方向为uˆ0=(θ0,φ0) =(30°，0°). 通过涡旋场典型的环形电场强度分布(图11(a))和螺旋相位分布(图11(b)) 说明高阶Bessel 波束与涡旋波束具有内在的关联性.

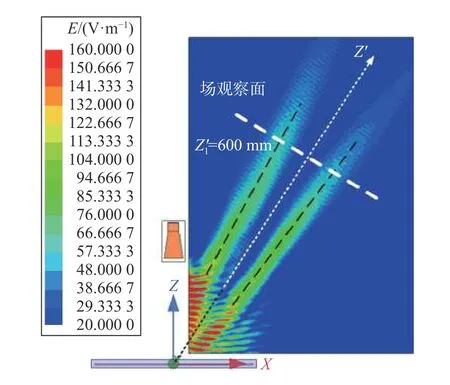
图10 单波束2 阶Bessel 波束在与波束传播轴平行的观察面内的电场强度分布Fig. 10 Electric field intensity distribution of the single beam Bessel beam of the second order in the observation plane

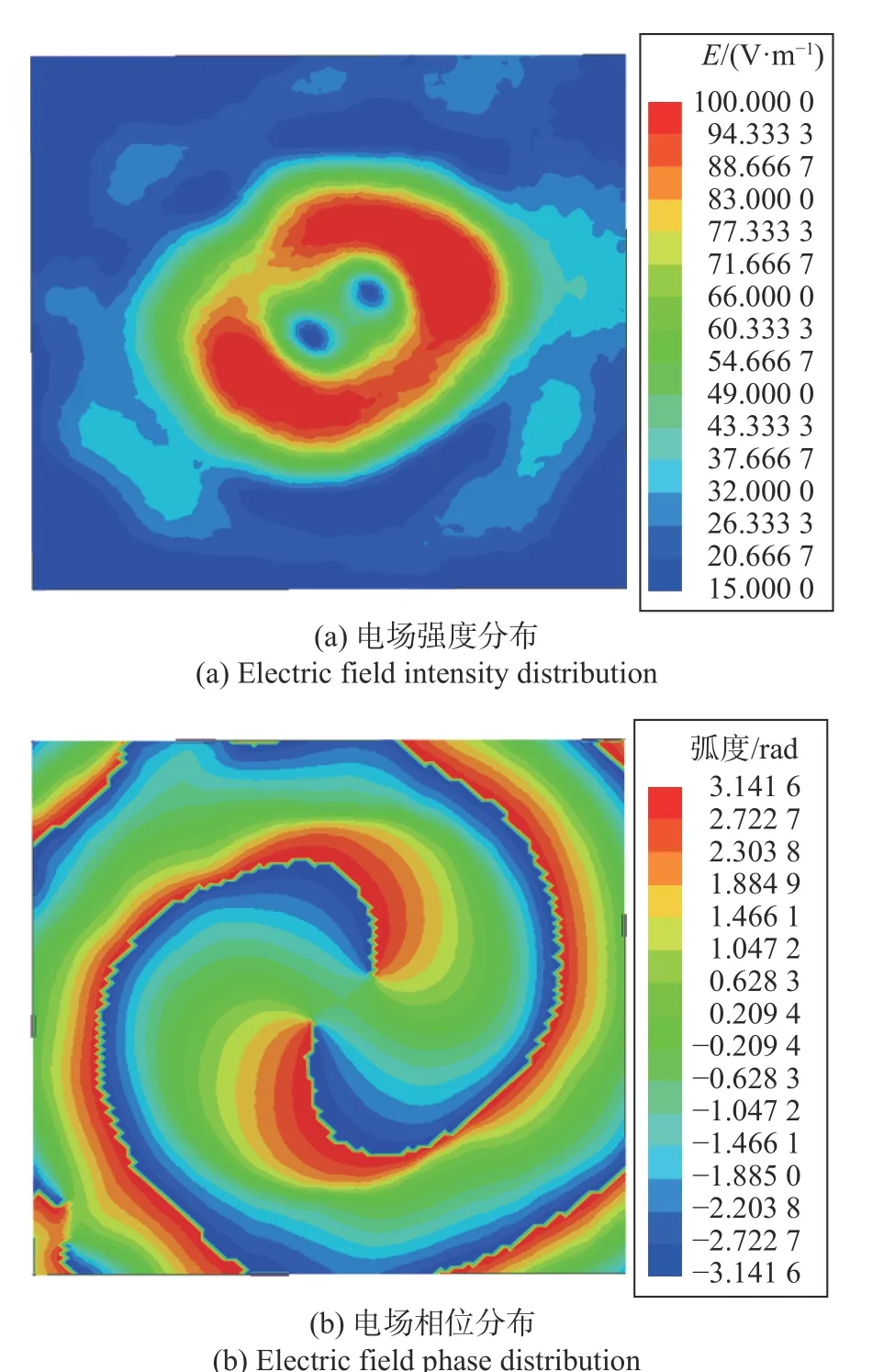
图11 单波束2 阶Bessel 波束在与波束传播轴垂直的观察面内的涡旋电场强度分布与相位分布Fig. 11 Electric field intensity and phase distribution of the single beam Bessel beam of the second order in the observation plane

基于式(11) 给出了一个双波束高阶Bessel 波束的设计，可以同时产生两个指向不同阶数ℓ也不同的Bessel 波束. 设计参数为：波束1 指向为uˆ1=(θ1,φ1)=(30°，0°)， ℓ1= 1；波束2 指向为uˆ2= (θ2,φ2) =(-30°，0°)， ℓ2= -1. 图12 和图13 分别为双波束高阶Bessel 波束在给定的空间观察面内的电场分布仿真结果. 可以看出，预期的波束方向产生了所要设计实现的高阶Bessel 波束，证明了设计的有效性.

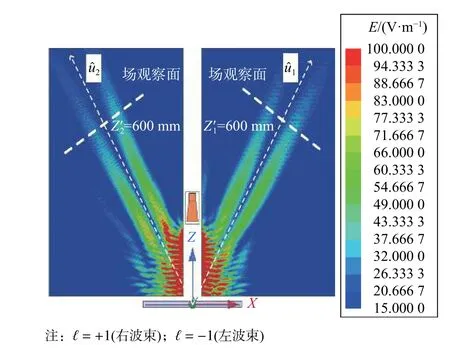
图12 双波束高阶Bessel 波束在与波束传播轴平行的观察面内的电场强度分布Fig. 12 Electric field intensity distributions of the dual Bessel beams of the first order in the observation planes

3 结 论

本文主要对多种不同类型Bessel 波束的产生设计原理和设计方法进行了介绍和梳理，并以反射型编码电磁超表面作为具体的实现方式，分别设计实现了零阶/高阶的单波束/双波束Bessel 波束，通过全波电磁仿真的方法分别仿真计算了对应不同类型Bessel 波束的空间电场分布特性，验证了设计方法的有效性. 编码电磁超表面作为信息超材料的一个重要研究分支，通过编码电磁超表面设计实现Bessel波束调控的方法可以进一步应用到有关的信息超材料系统的设计当中，有效促进Bessel 波束将来在近场无线能量/信息传输以及雷达探测与成像中的应用.