电压对马鞍脊面喷涂成膜特性影响的数值模拟研究
2022-01-08张淑珍马许杰惠志强刘大舜余刚
张淑珍,马许杰,惠志强,刘大舜,余刚
(兰州理工大学机电工程学院,甘肃 兰州 730050)
由于喷涂机器人具有效率高、服务好、保护工人免受危险工作环境影响等优点,因此广泛应用于机械、汽车、家具、航天等工业领域[1-3]。在喷涂过程中,雾化涂料流场被视为空气和涂料微粒的两相流,而静电空气喷涂雾化液滴通过外部感应荷电作用而荷电,属于复杂的荷电气液两相流问题[4-5],Hilton等[6]、Ye等[7]、Viti等[8]都采用了数值模拟和试验结合来研究静电喷涂成膜过程。数值模拟处理两相流的措施有欧拉−欧拉法及欧拉−拉格朗日法。在运用欧拉−欧拉法方面,杨庆功等[9]研究了平面喷涂,Chen等[10-11]研究了圆锥面、平面、内圆柱面和外圆柱面喷涂,然而该方法不能得出离散涂料液滴的运动轨迹;在运用欧拉−拉格朗日法方面,Pendar等[12]研究了平面喷涂,Domnick等[13]研究了平面、平面边缘和程式化车身后部喷涂,Ye等[14]研究了平面和阶梯平面喷涂,Osman等[15]研究了平面上凸起或凹陷喷涂,陈雁等[16]研究了球形面喷涂,Xie等[17]研究平面垂直、平面倾斜和圆柱形喷涂,该方法能解决欧拉−欧拉法研究中存在的问题。现有文献中静电喷涂的对象多为平面、圆柱面、圆锥面和球形面,但实际上被喷涂产品表面 形状复杂多样。马鞍脊面[18]具有形状类似马鞍及高斯曲率和平均曲率均小于零的特点,其喷涂过程中的流场分布、涂层厚度均匀性、涂料转移率等特性与相同喷涂参数下的平面相比有较大不同。由于电压是静电喷涂中重要的参数之一,因此有必要讨论喷涂电压对马鞍脊面成膜特性的影响,为优化喷枪喷涂作业轨迹和研发静电空气喷涂设备提供理论和参考仿真数据。
本文采用欧拉−拉格朗日法对喷涂电压为20、40、60和80 kV的静电空气喷涂成膜过程进行数值仿真,对气液两相流场和电场耦合作用下的喷涂域气相速度、涂料液滴粒径分布、电场分布和涂料液滴分布进行数值计算和分析,揭示喷涂电压对马鞍脊面喷涂成膜规律的影响。
1 静电空气喷涂过程模型的建立
在静电空气喷涂过程中,荷电液滴受气液两相流场、静电场等多场耦合作用,其运动轨迹的计算需建立多场作用模型。
1.1 喷涂静电场
外加的静电电压是影响静电雾化效果和雾滴运动轨迹的主要因素。由于静电场与流体之间存在耦合作用,因此本文基于麦克斯韦方程描述电磁场:
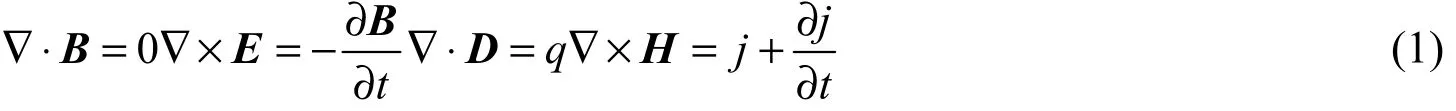
式中B为磁感应强度(单位:T),E为电场强度(单位:V/m),H为磁场强度(单位:A/m),D为电位移(单位:C/m2),q为粒子电荷密度(单位:C/m3),j为感应电流密度(单位:A/m2)。
感应场H、D之间的关系为:

式中μ为磁导率(单位:H/m),ε为介电常数(单位:F/m)。
采用电势法求解流场与电磁场耦合时的电流密度j,电场E可表示为:

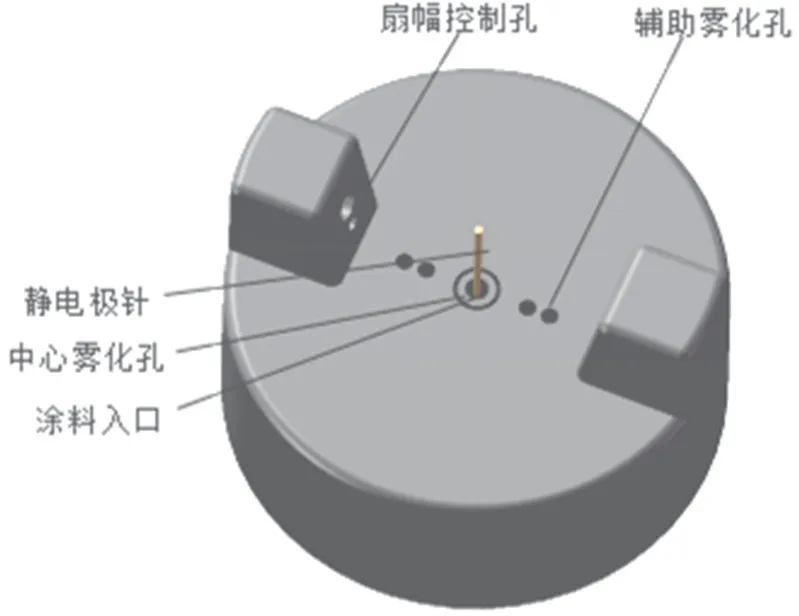
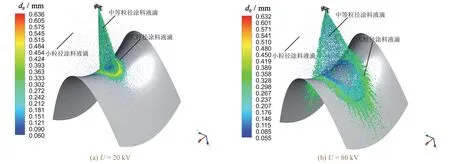
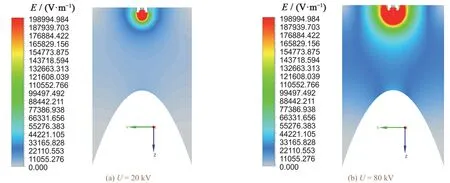
式中A为磁矢势(单位:V·s/m),φ为电势(单位:V)。对于静电场,b< 电势方程可表示为: 电势φ的边界条件可为: 在流体动量方程中引入附加源项来实现静电场耦合。流体动量方程的附加源项洛伦兹力F(单位:N/m3)表示如下: 电磁场中作用在带电涂料液滴上的洛伦兹力Fp(单位:N/m3)为: 式中qp为涂料液滴电荷密度(单位:C/m3),up为涂料液滴速度(单位:m/s)。 对于多相流动,忽略两相界面处的电流后,混合物的电导率σm(单位:S/m)为: 式中σi为第i相的电导率(单位:S/m),vi第i相的体积分数(无量纲)。σm用于感应方程求解。 喷涂流场被视为空气和涂料微粒的两相流,采用欧拉−拉格朗日法对马鞍脊面静电空气喷涂两相流模型进行建模。 1.2.1 连续相控制方程 整形和雾化空气流被视为连续相,其流动状态满足流体控制方程。在静电喷涂过程中,环境温度基本不变,因此忽略能量守恒方程。 质量守恒方程: 动量守恒方程为: 式中ρ为空气密度(单位:kg/m3),ui、uj分别为空气相在i、j方向的速度(单位:m/s),p为压力(单位:Pa),σij为黏性应力(单位:Pa),gi为重力体积力(单位:m/s2),Fi为外部体积力(单位:N/m3)。 1.2.2 离散相控制方程 液滴的运动轨迹通过力平衡方程来计算,其在拉格朗日坐标系中为: 式中u为气相速度(单位:m/s),ρp、ρ分别为液滴密度和气相密度(单位:kg/m3),FE为单位质量液滴的空间电场力(单位:N/kg),τr为液滴的弛豫时间(单位:s)。 式中μ为空气黏度(单位:Pa·s),dp为雾化液滴的直径(单位:m),Rer为相对雷诺数(无量纲),Cd为拖曳力系数(无量纲)。 对式(12)进行积分可得到液滴的速度: 对式(14)进行积分可得到液滴运动轨迹,再对其轨迹进行积分,可以得出液滴在喷涂流场中的湍流状态。 在静电空气喷涂中,空气流动属于湍流状态,需要建立相应的湍流模型来封闭动量方程。本文采用雷诺平均法中的可实现k-ε模型求解湍流效应。关于湍动能k和耗散率εd的输运方程如下: 式中Sk、Sε为自定义源项,YM表示可压湍流中的脉动扩张,C1、C2、C1ε、C3ε为经验常数,Gk、Gb分别表示平均速度梯度和浮力引起的湍动能k的产生项,Er为主流时均应变率,v表示空气运动黏度(单位:m2/s),μt为湍动黏度(单位:Pa·s),Prk、Prε分别表示k和εd对应的普朗特数。 荷电液滴输运至被喷工件形面过程中受到2种电场力:荷电液滴之间的电场力F1,以及荷电液滴与被喷工件形面之间的电场力F2: 式中E1为荷电液滴间的电场强度(单位:V/m),E2为荷电液滴与被喷工件形面之间的电场强度(单位:V/m),q为液滴带电量(单位:C)。 式中ε0为真空介电常数(单位:F/m),dm为荷电液滴间的距离(单位:m)。 式中U为荷电液滴云电压(单位:V),dn为荷电液滴与被喷工件形面的距离(单位:m)。 涂料液滴与被喷工件形面的碰撞有黏附、反弹、附壁射流、飞溅4种模式。为理解液滴碰撞模型,引入液滴韦伯数(We)作为判断碰撞模型的依据,其求解公式为: 式中un为荷电液滴法向速度(单位:m/s);di为荷电液滴输运至工件形面时的粒径(单位:m)。 喷枪模型的原型是美国固瑞克Pro Xp静电低压空气喷枪,喷枪空气帽如图1所示。模型中的静电极针直径是0.5 mm,最大输出电压为−60 kV,该模型的具体参数如文献[2]所述。 图1 静电喷枪空气帽模型示意图 Figure 1 Schematic diagram of air cap model of electrostatic spray gun 对喷枪空气帽的计算域进行非结构网格划分,如图2所示。空气帽位于上表面的中心处,计算域的下表面为被喷工件形面。考虑到空气帽的尺寸和数值模拟的要求,选用函数表达式为的马鞍脊面作为喷涂对象,计算域的长度和宽度均为300 mm,喷涂距离(涂料入口到喷枪轴线与目标交点的距离)为250 mm,坐标原点取涂料入口的圆心位置。 图2 马鞍脊面喷涂计算域 Figure 2 Calculation domain of saddle ridge spraying 采用Fluent软件进行数值计算。在气相流场中,除涂料入口外,其余入口均为质量流量入口;在液相流场中,涂料沿涂料入口面法线方向注入,设置涂料的质量流量为1.32 × 10−3kg/s,涂料黏度为0.096 86 kg/(m‧s),涂料密度为1 200 kg/m3,粒子粒径按照Rosin-Rammler分布。在MHD模型中,工件接地设定电压为0 V,极针电压为喷涂电压的设定值(分别为20、40、60和80 kV),时间步长Δt= 5 × 10−4s,喷涂时间为1 s。 3.1.1 喷雾流场形态 在静电空气喷涂中,涂料经喷嘴喷出,通过高压空气和施加的静电场共同作用将涂料雾化为液滴,而涂料液滴在电场力、喷枪轴向气流和库仑力的作用下向四周运动,在涂料液滴运动带动空气流动的同时,气流的运动又影响雾化液滴在流场中的运动,从而形成气液两相耦合的喷涂流场。由于气相速度变化更加显著,更能体现喷涂流场的扩展状态,因此选用气相速度分布云图对喷涂流场进行分析。 喷涂模拟发现,喷涂电压为20、40、60和80 kV时对喷涂流场特性的影响具有相似性,因此以喷涂电压为20 kV和80 kV时喷涂流场特性进行对比,为展示流场内部形态,截取沿XZ和YZ方向的气相速度云图,如图3和图4所示。为准确描述喷涂流场扩展状态,将其分为扩散区和成膜区,扩散区为涂料雾化的区域,成膜区为接近被喷工件形面的区域。 图3 不同喷涂电压下沿XZ向的气相速度云图 Figure 3 Cloud diagram of gas phase velocity along XZ direction under different spraying voltages 图4 不同喷涂电压下沿YZ向的气相速度云图 Figure 4 Cloud diagram of gas phase velocity along YZ direction under different spraying voltages 由图3和图4可看出,同一喷涂电压下,在扩散区中,喷涂流场向四周扩散的形态基本相同,在中心轴附近空气流速较大,靠近喷嘴处气流速度达到最大值,但喷涂流场气相速度随着流场扩散逐渐减小;在成膜区中,同一喷涂电压下,临近工件表面气流速度发生急剧变化,喷涂流场沿着被喷工件表面向周围扩散,气相速度继续减少,且喷涂流场沿YZ向比沿XZ向扩散得更远。在成膜区和扩散区中,随着喷涂电压增大,喷涂流场的覆盖范围逐渐向四周扩大。 不同喷涂电压下马鞍脊面喷涂流场形态有差异是因为被喷形面和喷涂电压的作用。喷涂电压对喷涂流场的影响规律表现为:涂料液滴之间存在斥力,随着喷涂电压的增大,电晕放电能力增强,涂料液滴荷电量增加,由库仑定律可知斥力也增大,使荷电液滴向四周扩散范围更大,同时涂料液滴带动空气向四周流动,体现在喷涂流场覆盖范围更大。马鞍脊面形面特点对喷涂流场的影响规律表现为:(1)在成膜区,当喷涂流场沿XZ向扩散时,由于此方向是从中心向外凹陷的曲面,喷涂扩散受到较大的阻碍,因此喷涂流场未完全展开;(2)当喷涂流场沿YZ向扩散时,由于此方向是从中心向外凸起的曲面,喷涂扩散受到的阻碍较小,因此喷涂流场覆盖范围大。 3.1.2 涂料液滴分布 由于喷涂电压对喷涂流场中涂料液滴分布有很大影响,而涂料液滴分布直接决定着喷涂成膜质量,因此对涂料液滴分布进行分析。喷涂电压为20、40、60和80 kV时对涂料液滴分布的影响具有相似性,喷涂电压为20 kV和80 kV的喷涂流场中涂料液滴粒径分布如图5所示。 图5 不同喷涂电压下喷涂流场中涂料液滴的粒径分布 Figure 5 Particle size distribution of paint droplets in spray flow field under different spraying voltages 从图5可看出:(1)不同喷涂电压下,小粒径液滴(100 μm以下)多数分布在喷涂流场的外围,且分布状态杂乱无章;(2)大粒径液滴(400 μm以上)基本分布在大粒径液滴输运过程所围成的圆锥面上,且分布状态井然有序;(3)中等粒径液滴(100 ~ 400 μm)大都分布在中等粒径液滴输运过程所围成的圆锥面上,且分布状态比较整齐有序。这是因为:中等粒径液滴和大粒径液滴由于自身质量和电场力的作用,不易被空气流动带动,而且粒径越大,涂料液滴所带的电荷量越大,因此涂料液滴之间受到的库仑力作用增大,导致粒径越大的液滴输运过程形成的喷锥角更大;小粒径液滴由于体积和质量小,受到电场力的作用较小,在扇幅控制孔的作用下,小粒径液滴横向速度增大,逐渐运动至喷涂流场外围。由于湍流的影响,少量的中等粒径液滴分布在流场外侧。 随着喷涂电压的增加,喷锥角逐渐增大,喷涂流场覆盖范围更广,被喷工件表面的涂料沉积分布范围扩大,涂层厚度变小,涂着率增大,涂层厚度均匀性增加。这是因为涂料液滴之间存在斥力,而随着喷涂电压的增大,电晕放电能力增强,涂料液滴荷电量增加,斥力也就增大,使荷电液滴向四周扩散范围更大,而且电场力的增大使得更多的荷电液滴沉积在工件表面。 从以上分析可得出:(1)大粒径液滴和中等粒径液滴是成膜的主要来源;(2)小粒径液滴因受到气流流动的影响较大,对成膜只起次要作用。 在施加的外部静电电压作用下,静电喷枪产生电晕放电,喷涂件电势为零,雾化液滴在电场力的作用下流向工件表面。喷涂模拟表明,喷涂电压为20、40、60和80 kV在空间中的电势和场强分布相似,且沿XZ向和YZ向的电势和场强分布相似,因此仅针对喷涂电压为20 kV和80 kV时沿YZ向的空间电势和场强分布来分析静电场。由于原始的场强分布云图中最大场强很大(107~ 108V/m),为了更直观地展现场强分布形态,将最大场强统一设定为200 kV/m。 从图6和图7可看出:(1)随着喷涂电压的增大,电势等势线更加密集,电场强度增大;(2)在同一喷涂电压下,喷嘴附近电势等势线的分布比较密集,电场强度也比较大,随着与喷嘴距离的增大,等势线比较稀疏,电场强度也减小;(3)设定最大场强相同时,随着电压的增大,同一场强覆盖范围增大。 所以在静电雾化中,在距喷嘴一定的范围内,液滴受到较大的电场力,加速破碎为细小液滴,之后随着场强的减小,液滴受到的电场力也逐渐减小。 图6 不同喷涂电压下沿YZ向的电势分布云图 Figure 6 Cloud diagram of potential distribution along YZ direction under different spraying voltages 图7 不同喷涂电压下沿YZ向的电场强度分布云图 Figure 7 Cloud diagram of electric field strength distribution along YZ direction under different spraying voltages 在喷涂过程中,不同喷涂电压下的马鞍脊面喷涂成膜质量各不相同,因此需要分析喷涂电压与喷涂成膜之间的关系,计算马鞍脊面上涂膜厚度(δ)分布云图,如图8所示。喷涂电压为20 kV的成膜分布为圆环状,喷涂电压为40、60和80 kV的涂膜分布为椭圆环状。不同喷涂电压下,环状成膜区域由内环向外环过渡时,涂膜厚度由小到大再到小。喷涂电压为20、40、60和80 kV的涂膜厚度最大值分别为0.454、0.250、0.169和0.136 mm,涂膜厚度整体随喷涂电压的增大而逐步变小,成膜面积越来越大,中心膜厚为零的区域面积越来越大,涂膜分布均匀性越来越好。 利用贴体坐标将图8中X轴与Y轴截面的涂料膜厚值导出,得到图9所示的不同喷涂电压下马鞍脊面沿X轴与Y轴截面方向的涂料膜厚分布图。 图8 不同喷涂电压下马鞍脊面涂膜厚度分布云图 Figure 8 Cloud picture of thickness distribution of coating on saddle ridge surface under different spraying voltages 从图9可看出:(1)在X轴和Y轴方向上,不同喷涂电压下马鞍脊面涂膜厚度分布都呈现出相似的变化规律,且喷涂电压越大,涂膜厚度分布越相似,但整体的涂膜厚度是逐渐下降的;(2)在X轴和Y轴方向上,不同喷涂电压下涂膜厚度从中心点(X= 0,Y= 0)到沉积最远处,膜厚经历了由小到大再到小的变化过程,且呈现出同样膜厚的双峰;(3)随着喷涂电压的增大,整体涂膜厚度逐渐减小,涂料沉积分布范围逐渐扩大,涂膜均匀性增加,涂膜厚度峰值逐渐远离中心点。 图9 不同喷涂电压下马鞍脊面涂膜厚度沿X轴(a)及Y轴(b)的分布 Figure 9 Thickness distribution of coating along X axis (a) and Y axis (b) on saddle ridge surface under different spraying voltages 从以上分析可知,喷涂电压对涂膜厚度主要有两个方面的影响:一方面,当喷涂电压增大时,喷涂流场扩散范围呈现出逐渐扩大的变化趋势,且使得涂料液滴荷电能力增强,同时涂料液滴之间斥力增大,使荷电液滴向四周扩散范围更大,而电场力的增大使更多的荷电液滴沿电场线方向运动到工件表面, 最终体现出涂料液滴撞击黏附在马鞍脊面的覆盖范围扩大,涂层变薄,涂料涂着率提高;另一方面,由于马鞍脊面上每一点到喷枪的距离不同,而且沿Y轴向上的喷涂区域比沿X轴向上的喷涂区域的喷涂距离更远,导致喷涂电压形成的电场力对荷电液滴的束缚作用更弱,使得喷涂距离近的区域涂层厚度增大,而喷涂距离远的区域涂层厚度变薄,表现出沿X轴向上的喷涂区域的喷涂厚度比沿Y轴向上的更大。 以喷涂电压为变量的马鞍脊面喷涂成膜数值模拟和喷涂成膜特性表现为: (1) 随着喷涂电压的增大,马鞍脊面喷涂时的喷雾流场覆盖范围扩大。同一喷涂电压下,沿XZ向和沿YZ向的喷雾流场形态在扩散区基本相同,但在成膜区,沿YZ向的喷雾流场扩散范围比沿XZ向更远;在中心轴附近空气流速较大,靠近喷嘴处气流速度最大,喷雾流场气相速度随着流场扩散逐渐降低。 (2) 随着喷涂电压的增大,电势等势线更加密集,电场强度增大;同一喷涂电压下,喷嘴附近电势等势线的分布比较密集,电场强度也比较大,离喷嘴越远则等势线越稀疏,电场强度也越小。 (3) 不同喷涂电压下涂料在马鞍脊面的沉积分布类似圆环形和椭圆环形。随着喷涂电压增大,涂膜覆盖范围逐渐扩大,涂层变薄,涂着率增大,厚度均匀性提高。同一喷涂电压下,由于YZ向上的喷涂距离比XZ向上更远,导致喷涂电压形成的电场力对荷电液滴的束缚作用更弱,因此XZ向上的涂膜厚度比YZ向上的更大。





1.2 气液两相流模型





1.3 湍流模型
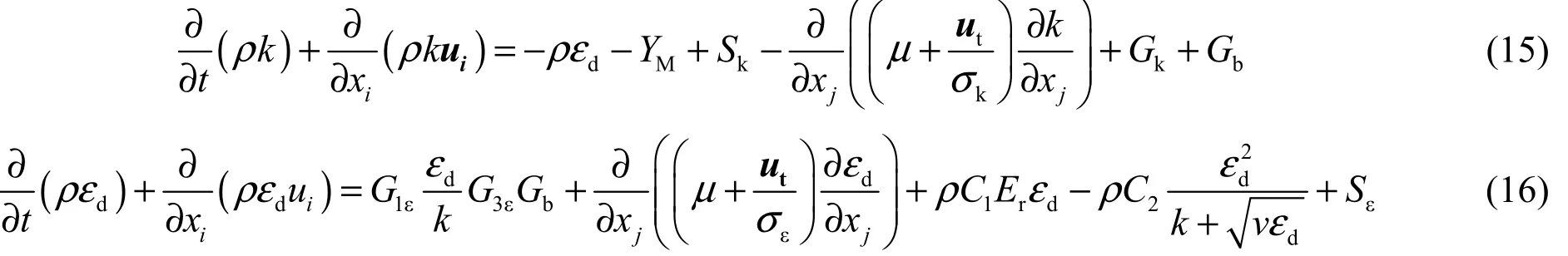
1.4 雾化液滴的输运和沉积过程




2 马鞍脊面喷涂过程的数值仿真
2.1 计算域模型的建立及网格划分

2.2 数值模拟参数和初始条件设置
3 数值模拟结果与分析
3.1 喷涂电压对喷涂流场的影响


3.2 马鞍脊面喷涂域静电场分析

3.3 喷涂电压与马鞍脊面喷涂成膜分布的关系


4 结论
