内填钢纤维混凝土-钢管束剪力墙压弯承载能力分析
2022-01-08张常涛傅明亮曾武华
张常涛,傅明亮,曾武华
(1.福建一建集团有限公司,福建三明 365001;2.福建农林大学 交通与土木工程学院,福建福州 350002;3.三明学院 建筑工程学院,福建三明 365004)
随着剪力墙体系应用于高层住宅钢结构中,寻找一种高性能、装配化程度高的剪力墙结构体系很有必要。2016年,付波[1]等提出的钢管束混凝土组合剪力墙结构受到广泛关注。张晓萌[2]对这一结构进行研究,表明其具有良好的承载能力和延性能力。钢管束剪力墙可根据实际需要布置成一字型、T型和L型等构造形式,充分发挥其装配灵活、施工便捷的特点,满足住宅建筑的发展需求。然而,在建筑向高强化演变的趋势下,钢管束剪力墙需要更优越的承载能力及延性。提高钢材强度及钢板厚度均可以满足这方面要求,但因其经济效应低而缺少使用。同时,提高混凝土强度也能增强构件承载能力,但其往往伴随着对构件延性的削弱。研究表明[3-4],钢纤维的掺入能有效改善混凝土的力学性能,钢纤维体积率较高时,可显著提高混凝土的抗剪强度、抗拉强度及其剪切韧性。因此,本文提出一种内填钢纤维混凝土-钢管束剪力墙结构,有望在增强构件承载能力的同时,能够有效提高构件延性能力。
由于剪力墙尺寸大,整体完全掺入钢纤维价格昂贵,经济效应低,将钢纤维混凝土应用于剪力墙构件时应按照“部分增强”的理论,即仅将钢纤维混凝土浇筑于剪力墙中应力复杂的部位。楚留声[5]进行了高强混凝土剪力墙在低周反复荷载作用下的试验,研究结果表明在边框加强与整体加强两种模式下,剪力墙承载力的差异并不显著,但相较于整体加强模式,边框加强模式不仅节省钢材,其制造成本也大幅降低。赵军[6-7]通过试验研究表明仅在剪力墙约束边缘构件内掺入钢纤维对结构的承载力及其延性均有一定提升效果。基于“部分增强”的思想,本文仅在钢管束边缘竖向部分掺入钢纤维,研究钢纤维的体积率、混凝土强度、轴压比等参数对钢管束剪力墙压弯性能的影响。
1 模型验证
1.1 钢纤维混凝土有限元模型的建立
钢纤维混凝土有限元模型的建立方法主要有两种:一是用钢纤维混凝土本构代替普通混凝土本构,这一方法虽然可以大大降低建模的繁琐性,但其难以准确反映随机钢纤维散落在混凝土中的增强效果;二是分离建立钢纤维与混凝土,并考虑钢纤维的随机分布,这一方法可以较为精确地反映出随机分布钢纤维对混凝土的增强作用,但钢纤维数量众多、体积小,在Abaqus中直接建立实体模型过于繁琐。因此,本文借助Python脚本生成随机分布的钢纤维,生成的随机分布钢纤维如图1所示。钢纤维以“Embeded”的约束形式内置于混凝土中。钢纤维截面形式为圆形,长径比为 60,弹性模量为210 GPa,抗拉强度为1 200 MPa,本构模型采用双折线模型。
图1 钢纤维随机分布于立方体的示意图
1.2 本构模型
混凝土采用塑性损伤模型,塑性损伤模型提供相异的拉压性能,适用于低围压、单调、循环等荷载工况,与文中模拟的剪力墙构件有较好的适配性,并引入规范[8]中的混凝土应力-应变关系描述混凝土受拉(压)行为。钢材则采用考虑了柔性损伤的双折线模型。
1.3 网格类型与接触模型
钢管束、混凝土与顶梁基础梁均选用三维实体单元C3D8R,减缩积分单元可以避免剪切闭绝问题,计算精度高。钢纤维选用桁架单元T3D2。对模型中钢管束与混凝土之间相对滑移进行了模拟,以“硬”接触和摩擦系数为0.4的“罚摩擦”模拟钢管束与混凝土间的法向行为与切向行为。钢纤维混凝土、钢管束与顶梁、基础梁的接触均选用束缚“Tie”约束。相关研究结果表明,构件在低周往复荷载或单调荷载作用下,两者力学性能响应基本一致[9]。为更好地观察各设置参数对构件承载力的影响,本文仅对其进行单调加载。
1.4 模型验证
为验证考虑钢纤维随机分布的有限元模型的准确性和可靠性,将有限元分析结果与张兆强等[10]完成的钢纤维混凝土方钢管短柱轴压试验结果对比。本文分析的试件尺寸为:100 mm×2.8 mm×350 mm,钢纤维体积率为0.50%,详细参数取值参考文献[10]。试件与有限元荷载(F)-位移(Δ)曲线的对比结果如图2所示。由图2可见,有限元模拟计算结果和试验结果总体上吻合较好。表1分别列出了试验结果和有限元分析的峰值荷载计算结果。从表1可见,有限元计算的峰值承载力与实验结果的误差为1.6%,有限元模型求解精度高。
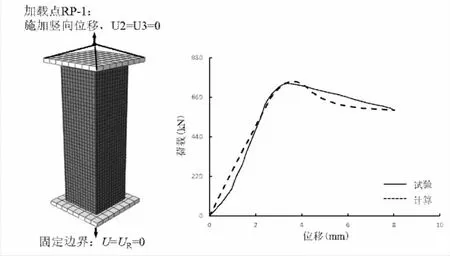
图2 验证的有限元模型及对比图

表1 钢纤维混凝土方钢管轴压试验与有限元分析的结果比较
2 参数分析
2.1 参数选取
研究表明[1-2],剪力墙的压弯性能与轴压比、混凝土强度、剪跨比、含钢率等参数有关。因此,本文主要分析钢纤维体积率、混凝土强度、轴压比、钢管束板厚等参数对构件压弯性能的影响规律。本文基准模型尺寸为:130 mm×2 056 mm×1 028 mm,采用验证的有限元模型方法建立基准模型,如图3所示。表2列出了在基准模型基础上变化构件参数得到的8个模型,通过有限元模型计算,得到每个模型对应的峰值承载力结果。
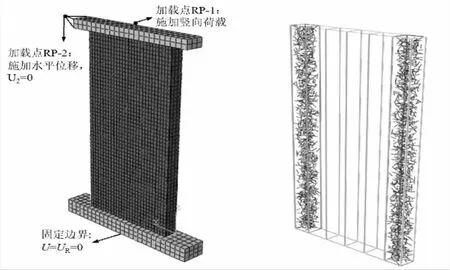
图3 构件有限元模型图(左)和钢纤维分布图(右)
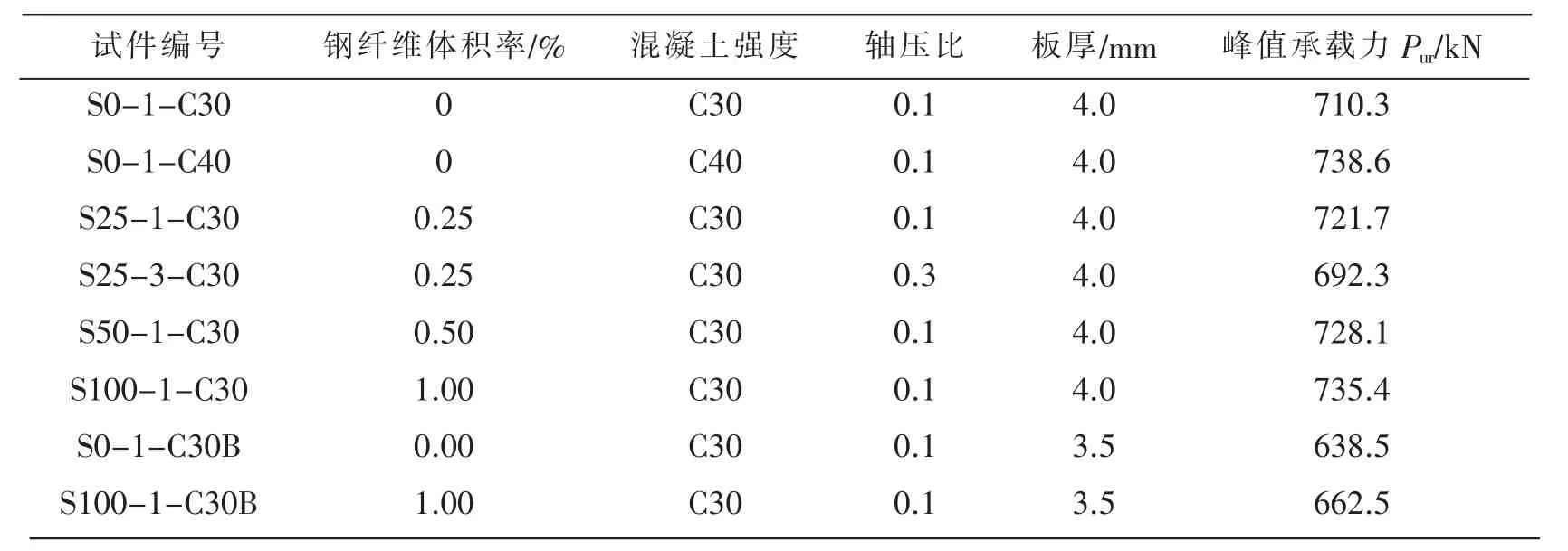
表2 构件参数及试验结果
2.2 钢纤维体积率
在混凝土中掺入钢纤维,可以改善混凝土的抗弯、抗裂性能[4];已有研究[5]表明,钢纤维掺入容易形成钢纤维团聚而影响构件性能,故本文仅模拟钢纤维掺量不超过1.0%的情况。设计了4个剪力墙试件 S0-1-C30、S25-1-C30、S50-1-C30、S100-1-C30,钢纤维体积率分别为 0%、0.25%、0.5%、1.0%,其余参数均相同。
图4给出不同钢纤维体积率下的荷载(F)-位移(Δ)曲线图。由图4可见,构件的受压弯峰值承载力随钢纤维体积率的增加而增大。通过与未掺入钢纤维的钢管束剪力墙构件比较,结果表明,掺入钢纤维体积率为0.25%、0.5%、1.0%时,构件峰值承载力分别提高1.6%、2.5%、3.5%。同时,掺入钢纤维钢管束组合剪力墙具有良好的延性。
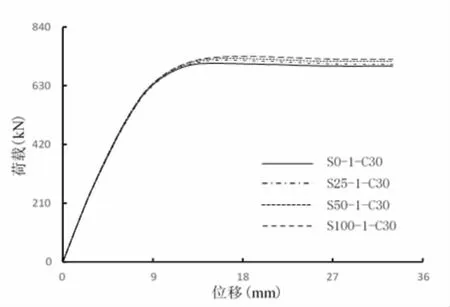
图4 不同贡献为体积率的荷载-位移曲线
2.3 轴压比
轴压比是剪力墙构件承载能力的主要影响因素之一[5],本文通过两个剪力墙构件分析轴压比对其承载力的影响。图5所示为不同轴压比下的构件荷载(N)-位移(Δ)曲线图。从该图可见,轴压比为0.1的构件,相较于轴压比为0.3的构件,其峰值承载力更高,且曲线下降更为平缓,延性较好。当轴压比为0.3时,钢管束已经进入弹塑性阶段而变形,影响了钢纤维混凝土与钢管束之间的相互作用,进而使构件承载力降低。
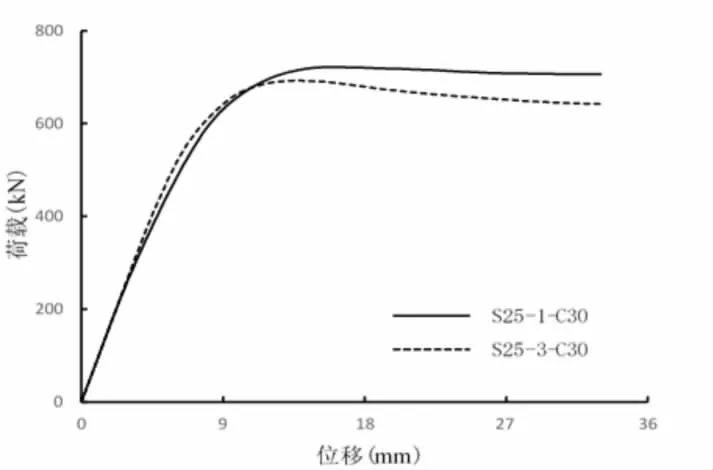
图5 不同轴压比的荷载-位移曲线
2.4 混凝土强度
图6给出了混凝土强度分别为30、40 MPa的钢纤维混凝土-钢管束剪力墙的荷载(F)-位移(Δ)曲线图。在分析这部分影响时,均考虑了混凝土的损伤。由图6可见,混凝土强度对构件承载力、初始刚度及延性均有一定影响,构件初始刚度及承载力均随混凝土强度的提升而增大,同时延性随之减小。
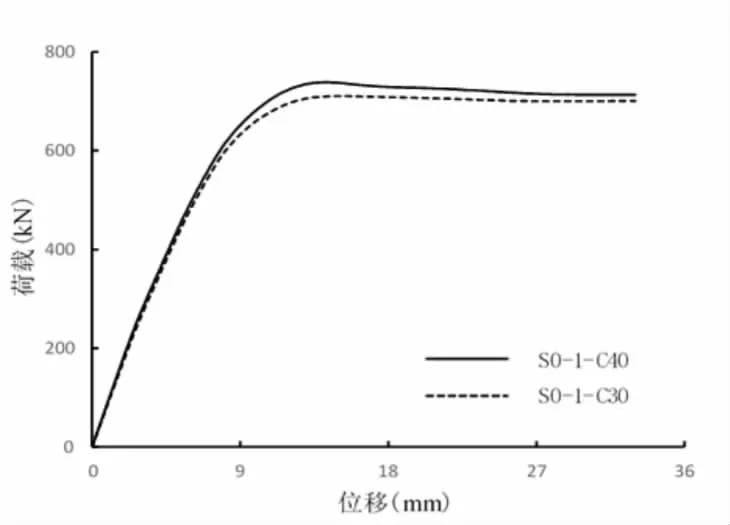
图6 不同混凝土强度的荷载-位移曲线
2.5 钢管束板厚
图7为不同钢管束板厚的荷载(F)-位移(Δ)曲线图,钢管束板厚对剪力墙构件的弹性刚度有明显的影响;在达到峰值荷载时,板厚对其承载能力的影响也较为显著。板厚从3.5变为4.0 mm,峰值承载力提高11.2%。保持板厚3.5mm不变,在钢管束边缘竖向部分掺入1.0%钢纤维时,构件承载力提高3.8%。因此,通过掺入一定量的钢纤维,可以有效提高钢管束剪力墙构件的承载能力及延性,达到与增加钢管束板厚相同的效果。
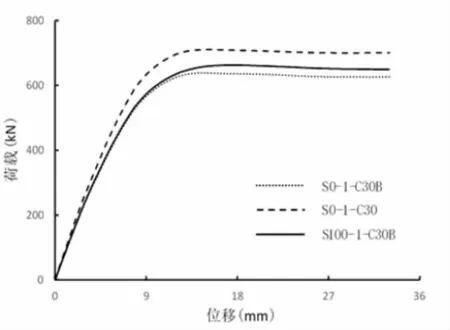
图7 不同板厚的荷载-位移曲线
3 结论
本文通过对内填钢纤维混凝土-钢管束剪力墙的压弯构件进行有限元模拟分析,得到以下结论:
(1)钢纤维体积率和混凝土强度的提高均能增大构件的极限承载能力。然而,混凝土强度的提高会降低构件延性,钢纤维的掺入在提高构件承载能力的同时不降低其延性。
(2)随着构件轴压比的增大,钢纤维-钢管束剪力墙的压弯承载力减小。
(3)钢管束板厚的增大,内部混凝土所受约束效应有所增强,构件承载能力随之提高。通过掺入一定量的钢纤维,可以达到与增加钢管束板厚相同的效果。
