大跨度高速铁路矮塔斜拉桥减隔震设计研究

万乐乐 季日臣 夏修身

兰州交通大学土木工程学院，兰州 730070

矮塔斜拉桥造型美观、跨越能力强、施工方便，但梁体自重大，对矮塔斜拉桥抗震不利。塔梁固结体系的矮塔斜拉桥全桥纵向刚度大、自振周期短，因此结构在地震作用下的内力响应较大。桥梁减隔震设计理念：①采用柔性支承以延长结构自振周期，使结构基频避开地震能量集中的频率范围，从而减小结构的地震响应；②采用阻尼式能量耗散元件为结构提供附加阻尼，从而减小柔性支承处的相对位移［1］。

自20世纪70年代以来，减隔震技术发展迅速，多种减隔震支座已应用于桥梁抗震设计中［2］，矮塔斜拉桥抗震研究较多。文献［3］对高烈度区的矮塔斜拉桥进行了减隔震研究，发现黏滞液体阻尼器对连续梁刚构体系矮塔斜拉桥减震效果较好。文献［4］对比了三种结构体系的矮塔斜拉桥的地震响应并进行减隔震研究，发现摩擦摆隔震支座对塔墩固结、塔梁分离体系的矮塔斜拉桥减隔震效果显著。文献［5］对某高速铁路桥梁进行减隔震研究发现摩擦摆隔震支座对7 m墩高的桥梁减震效果优于13 m墩高的桥梁。文献［6］以某矮塔斜拉桥为例，研究了黏滞阻尼器、速度锁定器和双曲面减隔震支座对矮塔斜拉桥的减隔震效果，结果表明黏滞阻尼器对内力与位移减震效果较好且副作用小。文献［7］发现采用减隔震混合装置对独塔斜拉桥的横向抗震效果明显。文献［8］研究了摩擦摆隔震支座系统对宽幅矮塔斜拉桥的减震效果，结果表明摩擦摆隔震支座可有效减小墩身内力。文献［9］以某矮塔斜拉桥为例，发现同时采用黏滞阻尼器和减隔震支座大大减小了减隔震支座引起的位移。文献［10］研究了三种减隔震装置对某大跨连续梁桥的减隔震效果，发现采用摩擦摆隔震支座后，固定墩的内力大大减小，但墩梁相对位移增大。

关于大跨度矮塔斜拉桥的减震研究较少，用于参考设计的资料还不完善。本文以一座主跨为224 m的塔梁固结体系高速铁路矮塔斜拉桥为例，分别采用黏滞阻尼器和摩擦摆隔震支座进行减隔震设计并对比减隔震效果，为此类桥梁的抗震设计提供参考。

1 工程概况

福厦客运专线雷公山双塔三跨式矮塔斜拉桥跨径组合为（118.1+224.0+118.1）m，主梁为单箱双室箱梁截面，主墩支点处箱梁高12 m，边跨直线段及中跨跨中梁高7.2 m。索塔形式为直立式桥塔，桥面以上塔高44 m，桥面以上塔的高跨比为1/5.09。斜拉索为双索面扇形布置，每个桥塔每侧对称布置9对斜拉索，斜拉索梁上间距为8 m，塔上间距为1 m。

2 模型建立

采用有限元分析软件MIDAS/Civil建立该矮塔斜拉桥的空间模型（图1）。主梁、主塔和桥墩采用空间梁单元模拟，斜拉索采用桁架单元模拟，每侧的斜拉索与相应位置处的主梁节点用弹性连接里的刚性连接，塔梁用刚性连接。恒载考虑了自重、二期恒载、温度和风荷载，活载采用TB 10002—2017《中国铁路桥涵设计规范》中的ZK活载。采用非线性连接单元模拟黏滞阻尼器与摩擦摆隔震支座，黏滞阻尼器用Maxwell模型模拟，由阻尼系数与阻尼指数确定该模型。摩擦摆隔震支座用摩擦摆隔震装置模拟，由等效刚度Keff、弹性刚度K和初始刚度Kp确定该模型。

图1 全桥有限元模型

3 地震动输入

该桥采用3组地震波进行非线性时程分析，并取3组地震波计算结果中的最大值。桥址场地类别为Ⅱ类，特征周期为0.45 s，抗震设防烈度为7度，地震动峰值加速度为0.1g。根据桥址的场地类别与特征周期，所选地震波的特征周期应与桥址场地特征周期接近或相同。3条地震波分别为1952年的Taft波、1971年的Sanfer波和1940年的El-centro波，对3条地震波的峰值加速度进行调整后输入，调整系数分别为0.621 1、0.456 6和0.339 0。地震动沿纵桥向和竖向同时输入，顺桥向地震动峰值加速度为0.1g，竖向地震动加速度取水平向的0.65倍［11］。

4 减隔震工况及计算结果分析

4.1 黏滞阻尼器

黏滞阻尼器一般由缸筒、活塞、阻尼通道、阻尼介质（黏滞流体）、导杆等部分组成。当结构因振动发生位移时，安装在结构中的黏滞阻尼器的活塞与缸筒发生相对运动。活塞前后的压力差使黏滞流体从阻尼通道中通过，从而产生阻尼力耗散振动能量，达到减轻结构振动响应的目的。在2#墩顶与梁体间布设4个黏滞阻尼器，见图2。其中，1#墩、2#墩和4#墩为活动墩，3#墩为固定墩。

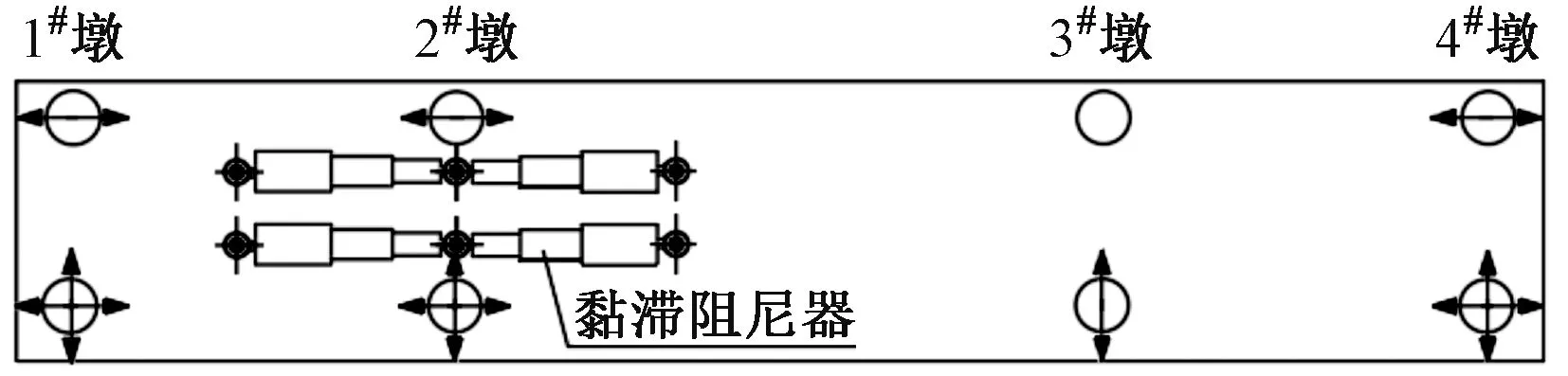
图2 黏滞阻尼器+普通球钢支座支承体系

黏滞阻尼器的阻尼力P为

式中：C为阻尼系数；v为参考速度；α为阻尼指数。

为得到适用于该桥减隔震装置的最优参数，对比不同阻尼系数与阻尼指数下的减震效果。α一般在0.1～1.0取值，分别取0.2、0.3、0.4、0.5；C取1 MN/（m·s-1）α，以1 000为步长逐级增加至7 MN/（m·s-1）α。以3#墩底纵向弯矩和剪力、3#墩顶位移、2#墩底纵向弯矩、2#墩墩梁相对位移和阻尼器最大行程为研究参量，对比不同减隔震参数对桥梁关键部位的内力及位移的影响规律，见图3。

图3 采用黏滞阻尼器后结构内力与位移及阻尼器最大行程变化曲线

由图3可知：

1）阻尼系数一定时，3#墩墩底纵向弯矩和剪力、3#墩墩顶位移、2#墩墩梁相对位移、阻尼器最大行程均随阻尼指数减小而减小，因此阻尼指数偏向于取小值。

2）阻尼指数一定时，3#墩墩底纵向弯矩和剪力、3#墩墩顶位移、2#墩墩梁相对位移和阻尼器最大行程随阻尼系数增大而减小，因此阻尼系数偏向于取大值。

3）2#墩墩底纵向弯矩随阻尼系数增大而增大，这是由于阻尼器发生运动时产生的阻尼力反作用于2#墩墩顶，使得2#墩墩底纵向弯矩有所增加。2#、3#墩墩底内力差值减小，对全桥的内力分布有利。

4）α=0.2时，3#墩墩底剪力在C=6 MN/（m·s-1）0.2之后出现增大趋势。因此，该桥减隔震采用黏滞阻尼器的最优阻尼参数为C=6 MN/（m·s-1）0.2，α=0.2。黏滞阻尼器的其他参数为输出阻尼力6 000 kN，设计行程100 mm。

4.2 摩擦摆隔震支座

摩擦摆隔震支座滑动曲面之间的摩擦使结构动能转化为热能，滑动曲面的摆动使结构运动周期延长，从而实现隔震功能。地震作用较小时，上部结构自重与支座间的静摩擦力可保证结构的稳定性；地震力较大时，支座按一定的周期滑动，将桥梁上部结构与下部结构的运动隔离，减小了下部结构的地震响应。实质上，刚度和周期控制可以选择合适的滑动面曲率半径来实现，减震消能控制可以选择合适的滑动摩擦系数来实现。全桥布置摩擦摆隔震支座后的支承体系见图4。

图4 摩擦摆隔震支座支承体系

摩擦摆隔震支座力的回复力F为

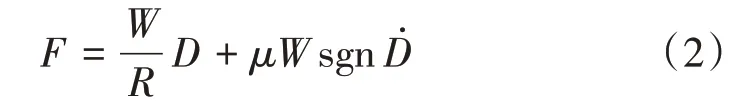
式中：W为支座在桥梁上部结构竖向荷载作用下的支反力；R为滑动球面的曲率半径；D为支座减隔震设计位移；μ为动摩擦因数，建议取0.05。

式（2）中，等式右边第一项为支座在上部结构荷载作用下沿曲面滑动时产生的水平回复力，第二项为摩擦摆隔震支座的球面滑动时产生的摩擦力。

支座等效刚度Keff为

弹性刚度K为

其中，支座弹性刚度取位移d y为2.5 mm时的刚度。

屈服后刚度Kd为

地震力较大时，摩擦摆隔震支座的剪力销被剪断，支座按一定的周期滑动发挥其减震功能，支座设计减隔震起始力（剪力销剪断时支座的水平力）为支座竖向承载力的10%。2#、3#墩支座承载力为180 MN，因此，其剪断力为18 MN。

为得到摩擦摆隔震支座的最优参数设计，对比分析结构在不同曲率半径和摩擦因数下关键截面的内力与位移响应。边墩采用不同曲率半径的摩擦摆隔震支座进行减隔震分析时，时程分析结果显示其减震效果不明显。考虑到使用经济性，对2#、3#墩支座进行分析。1#墩和4#墩摩擦摆隔震支座曲率半径取4 m，摩擦因数取0.04；2#墩和3#墩支座的曲率半径取3、5、7、9、11 m，摩擦因数取0.02、0.03、0.04、0.05、0.06、0.07。采用摩擦摆隔震支座后结构内力与位移变化曲线见图5。

图5 采用摩擦摆隔震支座后结构内力与位移变化曲线

由图5可知：

1）支座动摩擦因数一定时，2#墩和3#墩墩底弯矩随支座曲率半径的增大而减小，2#墩墩梁相对位移随摩擦摆隔震支座曲率半径的增大而增大，即摩擦摆隔震支座通过摩擦曲面的滑动将地震传递给桥梁结构的动能转化为热能而释放，从而减小了结构内力。但曲率半径递增到9 m后，2#和3#墩墩底弯矩、3#墩墩底剪力、3#墩墩顶位移的减幅与墩梁相对位移的增幅急剧减小。

2）当支座曲率半径一定，动摩擦系因数介于0.02～0.05时，2#和3#墩墩底内力、3#墩墩顶位移、2#墩墩梁相对位移随支座动摩擦因数的增大而减小，即摩擦摆隔震支座减震能力随动摩擦因数的增大而增大。

3）当支座曲率半径一定，动摩擦因数介于0.05～0.07时，2#和3#墩墩底内力、3#墩墩顶位移、2#墩墩梁相对位移随摩擦摆隔震支座动摩擦因数的增大而增大，减震能力减弱，这是由于动摩擦因数增大时，支座等效刚度也逐渐增大，即支座刚性的增强导致了隔震能力的减弱。当动摩擦因数无限增大时，抗震支座近似为普通桥梁支座，此时的抗震支座失去了减震耗能的作用。

4）地震作用下支座滑动面摩擦因数变化时，结构关键部位内力与位移的变幅较大，而支座曲率半径变化时，内力与位移的变幅较小，说明矮塔斜拉桥结构的地震响应对动摩擦因数的敏感性强于支座曲率半径。

综上，本文摩擦摆隔震支座的曲率半径取9 m，摩擦因数取0.05。

5 减隔震效果对比分析

以多重Ritz向量法分析对比矮塔斜拉桥结构在减隔震前后的前10阶动力特性，见表1。可知：①采用黏滞阻尼器时，结构前10阶频率和周期与原结构（未采用减隔震装置）相比完全一致。这说明在墩梁之间安装黏滞阻尼器进行减隔震后，阻尼器不会为结构提供刚度，对结构固有动力特性没有影响。②当斜拉桥结构采用摩擦摆隔震支座进行减隔震后，结构自振频率减小，自振周期是原结构的1.37倍，说明设置柔性支承有效地延长了结构自振周期。

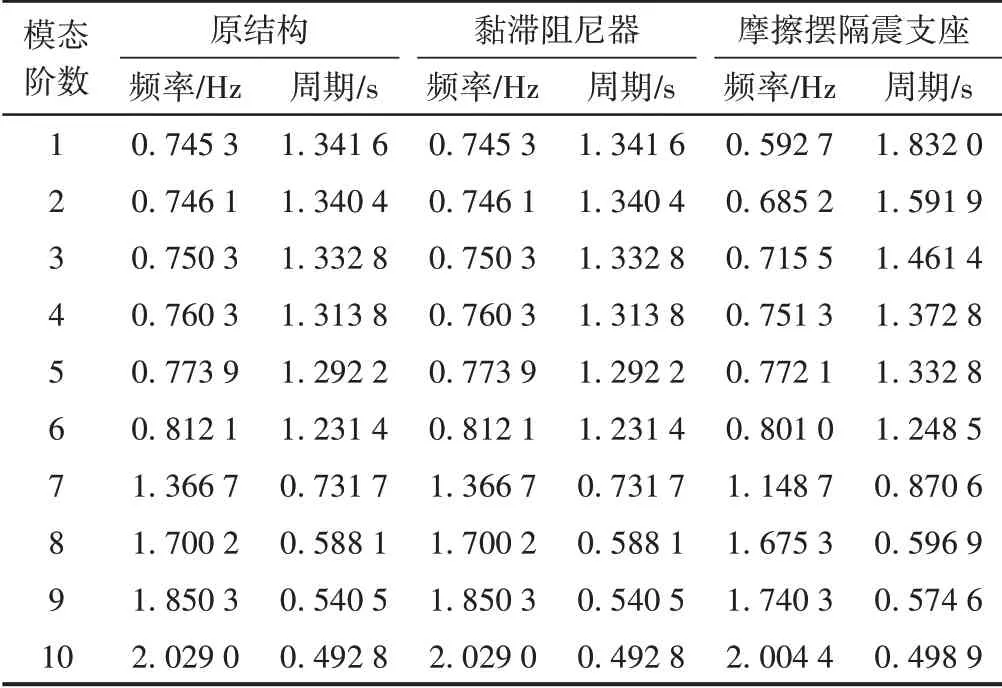
表1 动力特性对比

减震率w计算公式为

式中：θ为结构采用普通球型钢支座的计算结果；θ1为结构采用减隔震装置的计算结果。

对比矮塔斜拉桥结构在摩擦摆隔震支座和黏滞阻尼器最优参数下的内力、位移及减震率，分别见表2和表3。

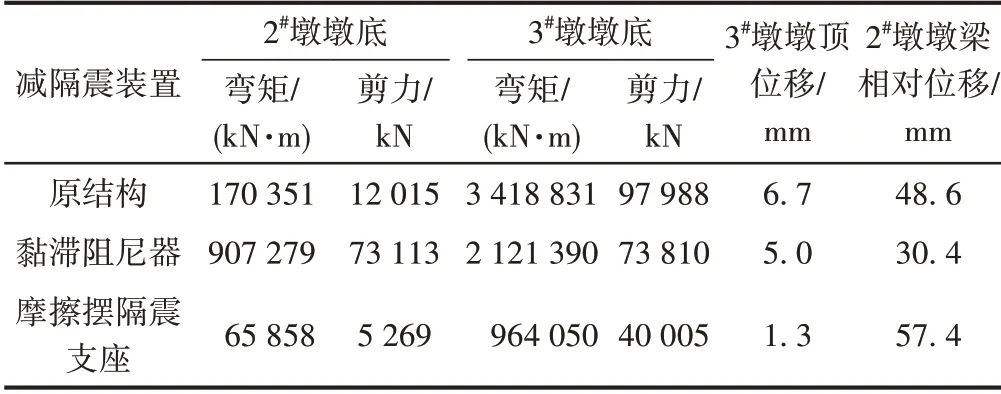
表2 结构关键位置内力及位移

表3 结构关键位置内力及位移减震率 %

由表2和表3可知：

1）对于原结构和采用了减隔震设施的结构，3#墩墩底内力比2#墩大，这是因为3#墩墩顶采用固定支座的纵向刚度较大，黏滞阻尼器虽然有效减小了2#墩墩梁相对位移，但导致墩底内力增加。由于桥墩刚度较大，墩顶位移较小，采用摩擦摆隔震支座后，3#墩墩顶位移减小更加明显。

2）采用黏滞阻尼器对结构进行减隔震设计时，2#墩墩梁相对位移和3#墩内力减小较明显。2#墩墩底弯矩和剪力分别增加了432.6%、508.5%，原因是阻尼器运动产生了阻尼力，其反力作用于墩顶，导致墩底内力增加，但2#、3#墩内力差值减小。

3）采用摩擦摆隔震支座进行减隔震设计时，2#、3#墩内力及3#墩墩顶位移减小明显，2#墩墩梁相对位移有所增加，原因是摩擦摆隔震支座通过大位移来实现摩擦耗能，从而减小了结构的地震响应。

4）两种减隔震装置均能减小结构的地震响应，但摩擦摆隔震支座的减震效果优于黏滞阻尼器+普通球型钢支座，因此采用摩擦摆隔震支座对该桥进行抗震设计更合理。

6 结论

1）原结构在地震作用下，由于固定墩墩顶支座的纵向刚度较大，全桥各墩底内力差异较大，分布不均匀。

2）采用黏滞阻尼器对结构的自振频率、周期等动力特性无影响，会引起活动中墩墩底弯矩与内力的大幅度增加，但主墩内力分布更均匀，可有效减小结构墩梁相对位移，但对桥墩内力减小作用有限。

3）结构采用摩擦摆隔震支座后，支座刚度降低，结构自振频率减小，自振周期延长，主墩内力及固定墩墩顶位移显著减小，实现了减隔震作用。

4）在全桥设置摩擦摆隔震支座后，内力与位移的变幅受支座动摩擦因数的影响强于支座曲率半径，即矮塔斜拉桥的地震响应对动摩擦因数的敏感性强于支座曲率半径。