低过采样Staggered SAR图像方位模糊抑制

廖杏杏 刘 喆 武俊杰

(电子科技大学信息与通信工程学院 成都 611731)

1 引言

传统合成孔径雷达(Synthetic Aperture Radar,SAR)无法同时获得方位向高分辨率和距离向宽测绘宽成像。为了解决该问题，Staggered SAR利用周期线性变化的脉冲重复间隔(Pulse Repetition Interval,PRI)和扫描接收(SCan-On-REceive,SCORE)技术实现连续观测的高分宽幅(High Resolution and Wide Swath,HRWS)成像[1]。由于Staggered SAR具有实现连续观测的HRWS成像的巨大潜力，其已被视为下一代星载SAR系统Tandem-L和NISAR的基本工作模式[1,2]。根据平均脉冲重复频率(Pulse Repetition Frequency,PRF)相对于多普勒带宽的比值，Staggered SAR可被分为高过采样和低过采样Staggered SAR。高过采样Staggered SAR发射信号过采样率一般为1.8～2.3[1,3,4]，其以增大发射和处理的数据量为代价降低丢失的影响，而低过采样Staggered SAR的发射信号过采样率可达到1.1[5]，大大降低了星载SAR数据存储负担和传输成本，因而得到了广泛关注。由于Staggered SAR存在变化的PRI引起的非均匀采样和由于收发冲突造成的数据丢失问题，因此有效处理这两个问题是获得高质量成像结果的前提。

处理高过采样率Staggered SAR数据一般有两种策略。第1种策略是对非均匀回波数据进行重采样使其均匀，然后应用传统SAR频域成像方法。最优线性无偏插值(Best Linear Unbiased,BLU)[1]、多通道重建(Multi-Channel Reconstruction,MCR)[1,3,5]等重采样技术均已在高过采样Staggered SAR中被成功应用。然而，BLU方法对PRI变化间隔较敏感，MCR只能在一个PRI变化周期中PRI序列较短的情况下有效工作。第2种策略是直接利用时域反投影(Back Projection,BP)算法或与其相似的频域方法。然而，由于低过采样以及丢失造成的欠采样问题，这两种策略都不能直接用于低过采样率Staggered SAR。为了解决这个问题，文献[5,6]提出了基于谱估计算法的两步处理方法，其中丢失数据迭代自适应算法(Missing Data Iterative Adaptive Algorithm,MIAA)[7]和高过采样Staggered SAR处理方法被依次用于恢复丢失数据和聚焦图像。然而，由于MIAA对频谱稀疏性的限制，且MIAA运算量较大，这种两步处理方法不能很好地用于分布式面目标场景。因此，现有的低过采样Staggered SAR方法无法完全有效抑制大场景面目标中的方位模糊，且效率低。

压缩传感(Compressive Sensing,CS)[8]技术已被广泛应用于欠采样SAR图像重建[9–16]。基于CS的成像算法按照构造的逆问题模型不同可以分为两类。第1类逆问题模型[9,10]基于回波与场景的时域关系构建，较长的重建时间和巨大的内存成本使得这类CS重建方法对大场景实测数据进行处理显得不切实际，因此往往只能用于处理较小的场景。为了降低基于场景向量化模型的CS算法中由测量矩阵和反射率向量直接相乘引起的较高计算复杂度，文献[11–16]提出了一类基于SAR回波频域模型(Frequency Domain Model,FDM)的CS成像方法。然而，这些基于FDM的CS重建方法或受限于窄带场景而不能完全补偿宽测绘带场景的距离徙动(Range Cell Migration,RCM)[11–13,15,16]或没有清晰、可微的表达式[11,14,15]，并且因为FDM没有处理低过采样Staggered SAR的非均匀采样、收发冲突造成的丢失和非理想天线方向图(Azimuth Antenna Pattern,AAP)问题，不适用于低过采样Staggered SAR。为了抑制非理想AAP造成的方位模糊，2013年Zhang等人[17]在基于时域回波模型的优化问题中嵌入了AAP导致的模糊区信息，但是该方法不能处理Staggered SAR存在的非均匀采样问题和宽幅场景下的RCM问题，且运算复杂度较高。

本文提出了一种创新的CS算法和选择滤波(Selective Filtering,SF)算法有机结合的成像方法。首先，针对低过采样Staggered SAR提出了一种创新性频域模型(Innovative FDM,IFDM)，其中精确的RCM首次在优化问题构造中被表示为多个非均匀离散傅里叶变换(Non-Uniform Discrete Fourier Transform,NUDFT)矩阵组成的三维张量；此外，非均匀采样和收发冲突造成的丢失分别由NUDFT矩阵和丢失指示矩阵表示。在该IFDM基础上，利用迹的性质以及张量和矩阵的微分，推导出了目标函数梯度的解析表达式，利用该梯度公式，二维快速迭代收缩阈值算法(2D Fast Iterative Shrinkage Thresholding Algorithm,2D-FISTA)[18]处理可得到抑制了非均匀采样和回波丢失造成的方位模糊的成像结果。最后，将迭代结果利用SF算法处理可抑制非理想AAP导致的模糊。为了提升本文方法的运算效率，利用快速傅里叶变换(Fast Fourier Transform,FFT)和非均匀快速傅里叶变换(Non-Uniform FFT,NUFFT)操作实现迭代更新过程中的离散傅里叶变换(Discrete Fourier Transform,DFT)和NUDFT矩阵乘。

本文的后续结构如下：第2节介绍了低过采样Staggered SAR信号模型，并分析了低过采样、回波丢失、非均匀采样及非理想AAP对方位模糊的影响；第3节详细介绍了所提出的方法；第4节给出了点目标仿真和RADARSAT-1模拟回波数据处理的实验结果，验证了所提出方法的优越性；第5节得出本文结论。

2 Staggered SAR原理

2.1 回波模型

系统采集到的Staggered SAR回波由瞬时采样时刻以及到达回波与发射脉冲的冲突关系共同决定。解调和距离压缩后，Staggered SAR的回波可表示为

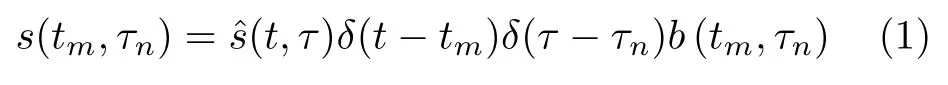
其中，τn表示距离时间τ的瞬时采样时刻，τn2rref/c+(n −N/2)/fsr,n0,1,...,N −1,rref为参考点斜距，c为光速，fsr为距离向采样频率，N为距离时间采样点数；tm表示方位时间t的瞬时采样时刻，由重复非均匀PRI序列决定，可表示为式(2)；sˆ是无丢失回波信号的连续时间形式，可表示为式(3)；b指示回波信号是否受收发冲突影响而丢失，可表示为式(4)。

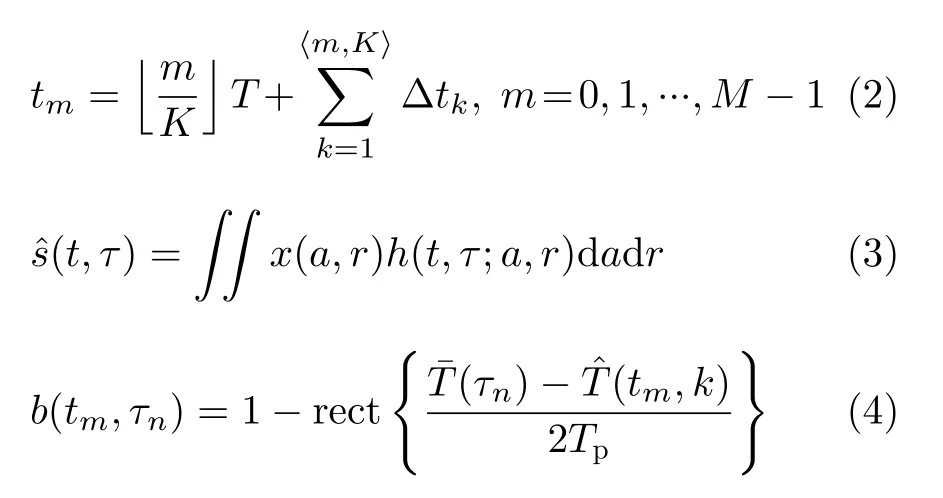
式(2)中，和〈·〉分别表示为向下取整和取余算子，M为发射脉冲的个数，Δt1～ΔtK为一个脉冲重复周期T的PRI序列，K为一个脉冲重复周期T内的脉冲个数，。式(3)中，x(a,r)表示点散射系数，a和r分别为点的方位向和距离向位置；h(t,τ;a,r)sinc(Wr(τ −τd(t;a,r)))exp(−j2πξ0·(τ −τd(t;a,r)))为点散射响应，其中ξ0和Wr分别为中心频率和发射信号带宽，τd为t时刻发射信号的收发时延，v为平台速度。Staggered SAR的τd中t和r存在耦合，与传统SAR产生RCM的原理一致。式(4)中，Tp表示发射脉冲宽度；

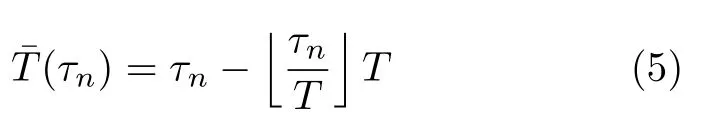
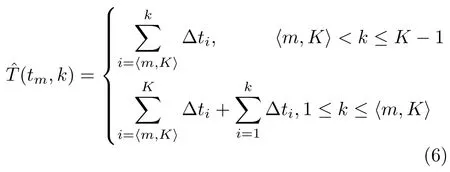
其中，k表示回波到达时刻位于发射脉冲间隔Δtk+1内，因此，b(tm,τn)0表示tm时刻发射脉冲在τn时刻后的回波信号由于收发冲突而丢失，b(tm,τn)1表示回波信号被成功接收。

基于以上分析，低过采样Staggered SAR回波是非均匀采样且存在丢失的，且丢失会导致欠采样的问题，此外，还存在RCM和非理想AAP的问题，其中非理想AAP指的是雷达波束同时使用主瓣和副瓣照亮观测场景，波束方向图主瓣外沿以及副瓣的接收能量会造成图像中出现方位模糊[19]。在低过采样Staggered SAR成像中，必须仔细考虑以上这些因素，才能有效抑制方位向上所有的模糊。

2.2 方位模糊分析

由式(1)可知，因为Staggered SAR系统使用的PRI是周期线性变化的，其接收回波在方位向是非均匀采样的，导致其方位频谱混叠与传统SAR存在一定差异。这会造成传统SAR成像方法对Staggered SAR回波直接处理的结果在真实目标方位向上出现多对较弱的方位模糊。以下将理论分析Staggered SAR成像结果中存在方位模糊的原因。

首先分析非均匀采样对方位模糊产生的影响。由PRI周期线性变化规律，回波方位向逐点采样公式可以写为M/K

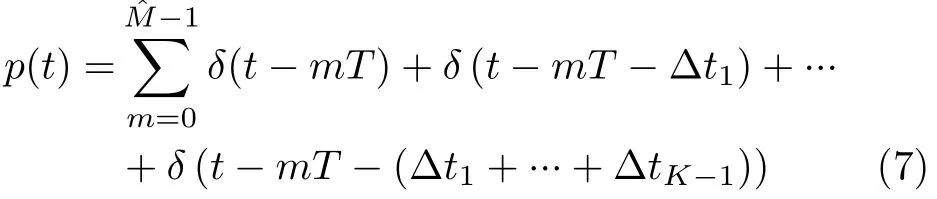
其中，为PRI变化周期个数。

定义回波连续信号为s(t)，按照式(7)对其进行采样的结果为

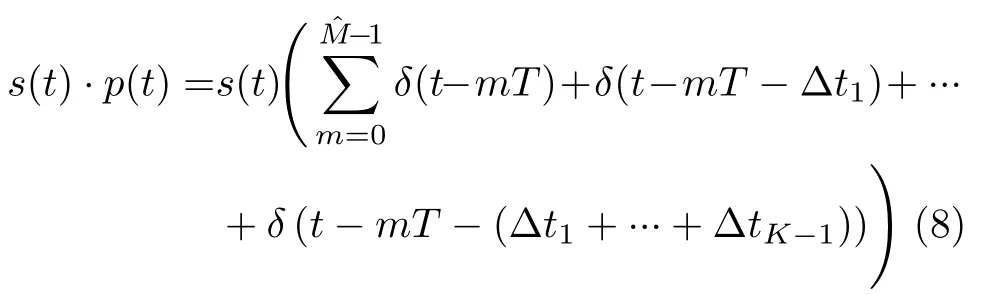
s(t)采样后对应的频域信号可表示为

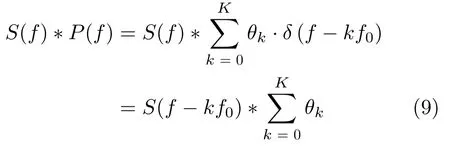
其中，∗代表卷积运算，(mT+Δt1+...+Δtk)(f −kf0),f0是PRI变化周期T对应的频率，f01/T,k0,1,...,K。

从式(9)给出的回波方位频域信号表达式可知，多个加权系数为θk的频谱叠加会造成Staggered SAR回波方位频域信号存在频谱混叠，且相邻加权结果的中心频率相差f0,f0PRFmean/K。式(9)中考虑了非均匀采样和雷达系统非理想AAP造成的频谱混叠。具体地，式(9)中θ0对应基带AAP,θk(k1,2,...,K −1)对应非均匀采样造成的加权AAP,θK对应雷达系统非理想AAP。图1(a)和图1(b)分别给出了高过采样和低过采样Staggered SAR的AAP混叠示意图，其中基带AAP用红色实线表示，f0对应的由非均匀采样造成的加权后AAP用绿色虚线表示，PRFmean对应的雷达系统非理想AAP用蓝色虚线表示。因此，Staggered SAR成像结果中真实目标方位向会出现由非均匀采样造成的多对均匀分布较弱的模糊，以及由非理想AAP造成的一对相对较强的模糊。

由图1可知，高过采样Staggered SAR相较于低过采样Staggered SAR有较大的 PRFmean，可以有效减小一个PRF周期内由 PRFmean处频谱混叠引起的方位模糊，同时kf0(k1,2,...,K −1)处频谱混叠引起的多对方位模糊也相对较弱。而低过采样Staggered SAR的 PRFmean较小，且可能存在由于回波丢失造成的欠采样问题，因此 PRFmean处和kf0(k1,2,...,K −1)的频谱混叠都要比高过采样Staggered SAR更加严重，导致低过采样Staggered SAR的成像质量大大差于高过采样Staggered SAR。在实际情况中，图1中基带AAP左右两边都存在由非理想AAP和非均匀采样造成的混叠，因此方位模糊在真实目标两侧相同位置偏移处成对出现[20]。

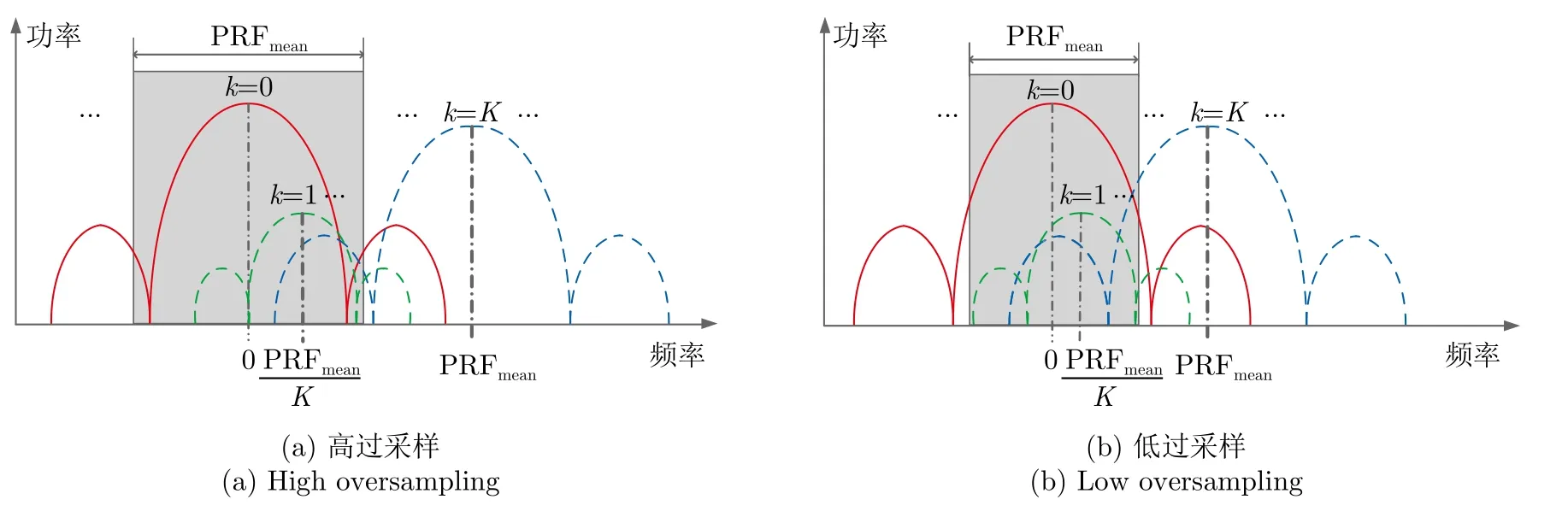
图1 Staggered SAR 天线方向图混叠示意图Fig.1 Map of azimuth antenna pattern aliasing for Staggered SAR

3 基于CS的模糊抑制成像

3.1 逆问题构造

首先，利用无丢失回波的频谱对无丢失回波sˆ(tm,τn)进行建模。根据式(1)，(tm,τn)具有非等间隔的方位瞬时时刻tm和等间隔的距离瞬时时刻τn，可表示为其二维频谱的二维逆傅里叶变换(Inverse Fourier Transform,IFT)得到，过程如式(10)所示。

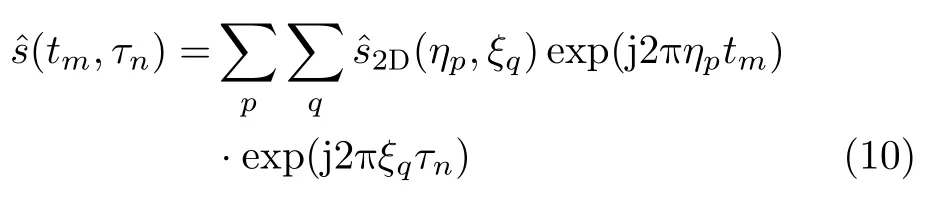
其中，ηp和ξq分别是离散多普勒频率和离散距离频率，

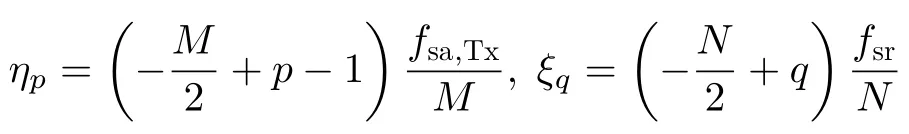
fsa,Tx为方位向发射信号采样频率，p0,1,...,M −1,q0,1,...,N −1 ;是(tm,τn)的二维频谱。对式(3)进行二维傅里叶变换(Fourier Transform,FT)并利用驻定相位原理，可以得到的解析式为

将式(12)中的算子用矩阵或三维张量表示，使得回波模型可以表示为一系列矩阵乘法运算：

接下来，利用回波时域丢失信息对接收到的Staggered SAR信号建模。根据式(1)可以得到无丢失回波和实际接收回波在时域上的关系为s(tm,τn)sˆ(tm,τn)b(tm,τn)。结合该时域关系以及式(13)，可以得到实际接收信号对应的IFDM为

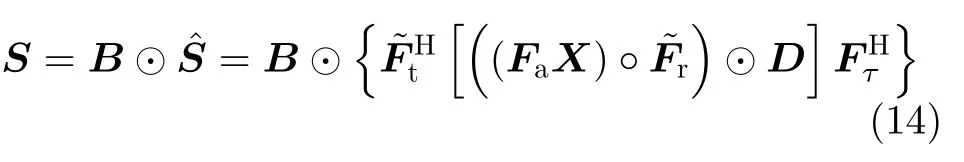
3.2 逆问题求解及选择滤波处理

低过采样Staggered SAR的图像重建过程等效于利用式(14)从回波矩阵S中提取反射率矩阵X，这是一个可用CS技术求解的不适定逆问题。给定一个稀疏化算子 Ψ，将反射率矩阵X变换为稀疏矩阵，即ΓΨ(X),Γ为稀疏矩阵，则式(14)中的逆问题可转化为以下优化问题：

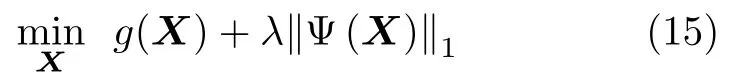
其中，‖·‖1表示矩阵1范数，λ>0是正则化参数，g(X)可表示为

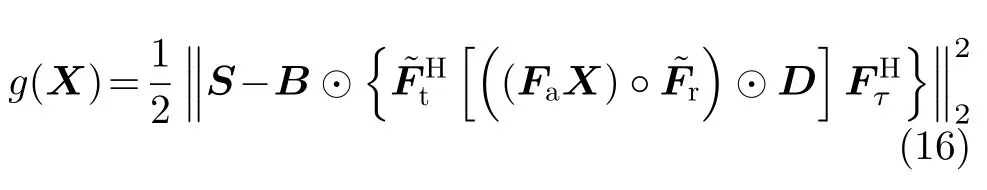
其中，‖·‖2表示矩阵Frobenius范数。

式(15)中的优化问题是一个ℓ1正则化的最小二乘问题。本文采用基于软阈值和梯度下降的2D-FISTA方法来解决该问题。应用2D-FISTA的核心是推导∇g(Γ)的解析式，即g关于Γ的梯度。由文献[12,15]可知，近年来Daubechies小波已被成功应用于欠采样SAR等遥感领域中，可以针对欠采样SAR实现高质量成像。因此，本文采用Daubechies-4小波[21]作为稀疏化算子，XΨ−1(Γ)。根据矩阵迹的性质，可得到

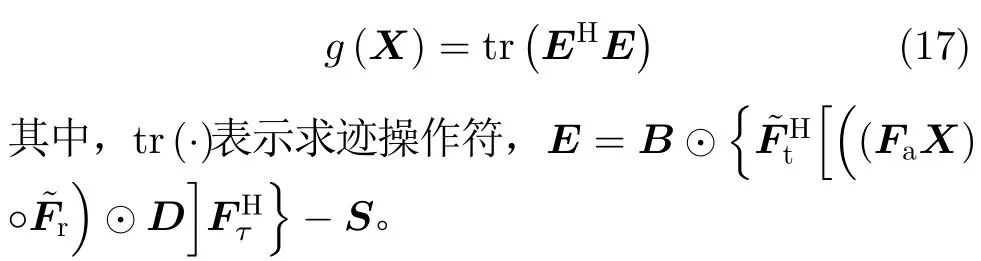
根据矩阵微分和梯度之间的关系，可以得到式(17)的梯度表达式为

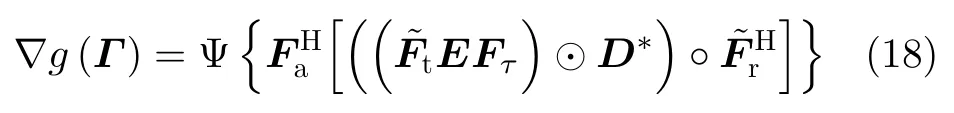
其中，(·)∗表示矩阵的共轭运算。

利用式(14)的IFDM和式(18)的梯度公式，求解式(15)的优化问题的方法称为IFDM-FISTA[22]。IFDM-FISTA将低过采样Staggered SAR成像模糊抑制问题看作一个从低过采样Staggered SAR回波中提取场景目标信息的逆问题，并利用CS优化技术求解该逆问题。与采用前向正问题模型的传统成像算法不同，IFDM-FISTA在逆问题求解过程中，不受奈奎斯特采样定理约束，可以有效抑制低过采样Staggered SAR由于回波欠采样引起的频谱混叠造成的方位模糊。并且，IFDM考虑了非均匀采样影响，因此IFDM-FISTA可得到抑制回波丢失和非均匀采样影响的低过采样Staggered SAR成像结果。最后利用SF算法[23]处理可抑制非理想AAP的影响，得到方位模糊全部被抑制的成像结果Xfinal。

本文结合IFDM-FISTA和SF，提出了IFDMFISTA-SF方法，并在表1中进行了总结。在表1中，初始化参数选取范围依据文献[18,24]；ℓf确定梯度下降步长[24]；表示以U(l)元素为导向的软阈值函数，其[m,n]th元素的值为，其中(·)+在输入项大于等于0时输出输入项本身，否则输出0；SF(·)表示选择滤波处理。由表1可知，本文方法每次迭代的计算复杂度由步骤3和步骤4决定，这两个步骤所有关于DFT和NUDFT矩阵的矩阵乘法都是通过FFT或NUFFT实现的，共包含M点FFT和NUFFT运算各 2N次，N点FFT和NUFFT运算各2M次，MN点哈达玛乘积3次，因此IFDM-FISTASF方法的计算复杂度为O(LMNlog2(MN))。

表1 IFDM-FISTA-SF流程Tab.1 The process of IFDM-FISTA-S

4 实验验证

为了验证IFDM-FISTA-SF方法抑制低过采样Staggered SAR成像结果中方位模糊的有效性，给出了点目标仿真和RADARSAT-1宽幅场景模拟回波数据处理的实验结果。为了定量分析各方法对方位模糊的抑制能力，使用最大模糊和真实目标幅值比(Ambiguity-to-Target Ratio,ATR)和积分旁瓣比(Integrated Sidelobe Ratio,ISLR)来评价，其中ATR20lg(iA/iT),iA为真实目标方位向最大的模糊，iT为真实目标幅值，ISLR计算只考虑除非理想AAP外的其他因素(回波丢失，非均匀采样)造成的模糊。除本文提出的方法外，还采用ωK直接成像方法演示非均匀采样和回波丢失的影响，为进一步支撑本文论点、凸显本文算法处理非稀疏宽幅场景面目标的优势，本文选取的发射信号过采样率与文献[5]相同，在此条件下与文献[5]所提出的方法进行比较、分析。实验的硬件配置采用Intel(R)Core(TM) i7-10700F处理器，32 GB内部存储器，软件环境为MATLAB 2017a。

4.1 点目标仿真

低过采样Staggered SAR点目标回波仿真参数如表2所示。由于点目标仿真回波未添加噪声，IFDM-FISTA-SF 算法的初始化参数可设置为λβ0[24]。图2给出了不同方法对低过采样Staggered SAR点目标回波的处理结果，红色实线、红色虚线和绿色虚线标注处分别为真实目标、非理想AAP造成的模糊和非均匀采样造成的模糊的位置。表3列出了图2中不同方法对点目标方位模糊抑制效果的性能评估对比。

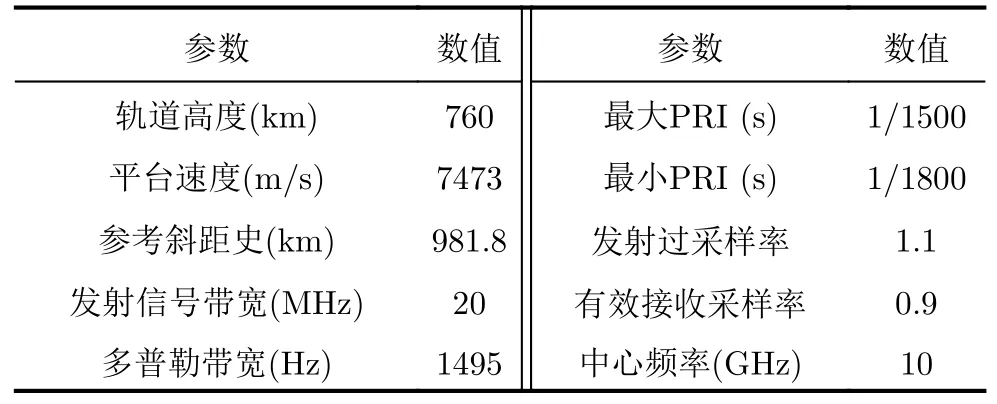
表2 低过采样Staggered SAR仿真参数Tab.2 Simulation parameters for low-oversampled Staggered SAR

从图2可以看出，ωK方法的处理结果中存在多对沿着真实目标方位向较弱的模糊和一对较强的模糊，分别处于非均匀采样和非理想AAP影响所在的方位位置。图2(b)和图2(c)表明对于孤立点目标，MIAA-MCR和IFDM-FISTA方法都能很好地抑制非均匀采样和回波丢失造成的方位模糊，但是非理想AAP造成的较强方位模糊仍然存在。图2(d)表明IFDM-FISTA-SF方法继承了IFDM-FISTA算法抑制非均匀采样以及回波丢失造成的方位模糊的能力，同时SF可以进一步抑制非理想AAP造成的模糊，从而实现高质量成像。表3中的结果同样表明IFDM-FISTA-SF能够最好地抑制各种因素造成的方位模糊。具体地，IFDM-FISTA-SF的ISLR−14.18和ATR−33.56分别表明其对丢失及非均匀采样和非理想AAP造成的模糊抑制效果优于其他方法。接下来，将对比分析各方法对面目标中方位模糊的抑制效果。

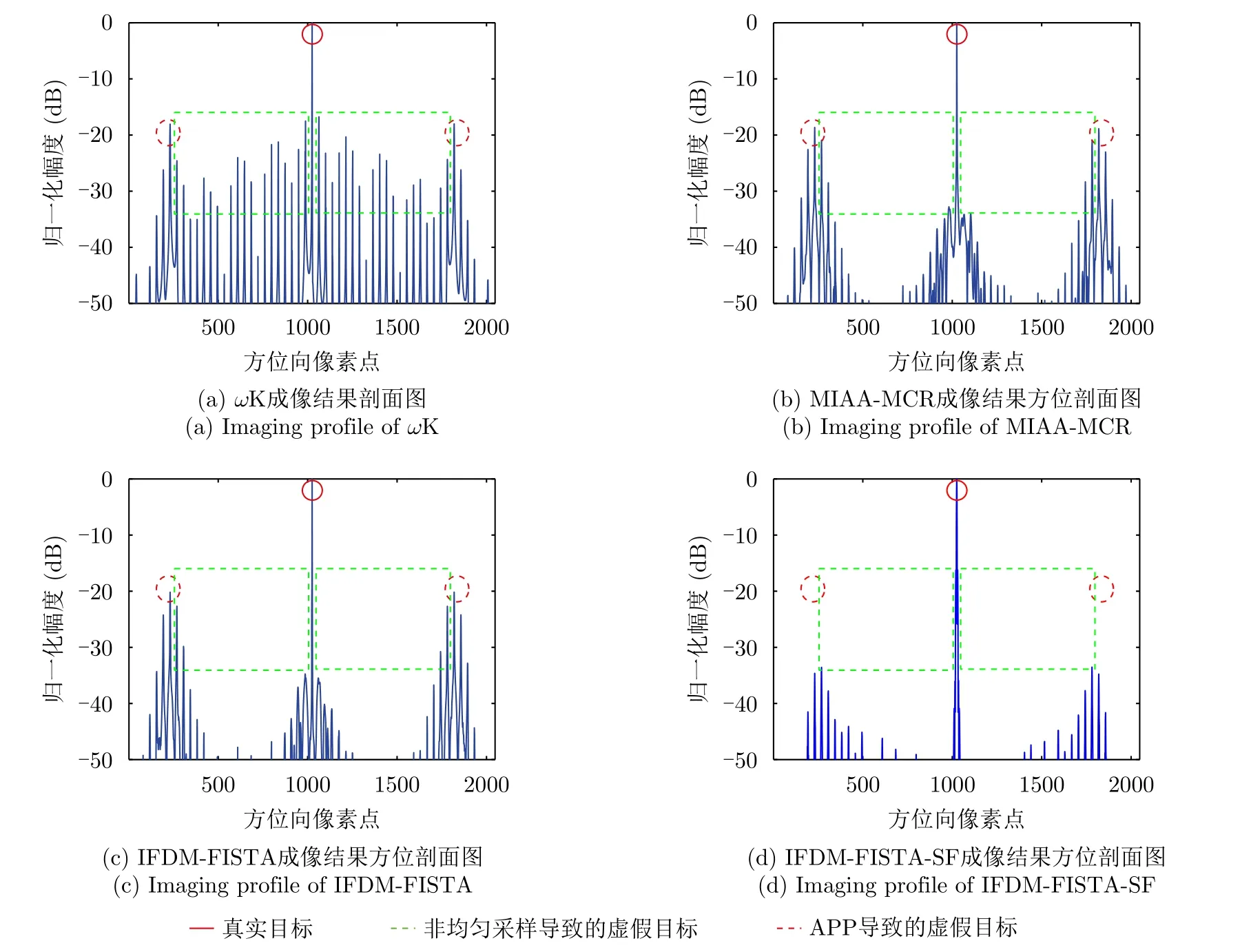
图2 点目标成像结果方位剖面图Fig.2 Azimuth profiles of reconstructed results for a point target

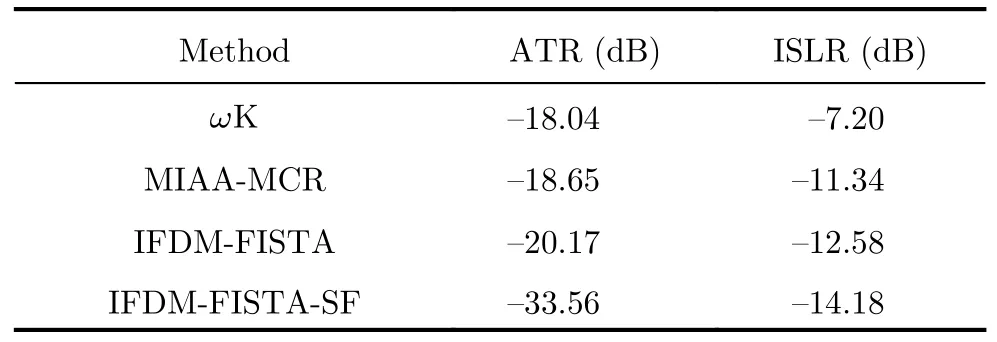
表3 不同方法对点目标模糊抑制性能的评估结果Tab.3 Evaluation results of the azimuth-ambiguity-removal performance for different methods

4.2 基于RADARSAT-1模拟回波数据的处理

本文利用文献[4,16]的数据模拟方式对加拿大温哥华地区RADARSAT-1覆盖范围为20 km×20.5 km(方位向×距离向)的宽幅场景对应的原始回波数据进行处理，获得宽幅场景下低过采样Staggered SAR模拟回波数据。根据L曲线法[25]，IFDM-FISTA-SF算法处理以上低过采样Staggered S A R 宽幅场景模拟回波数据的初始化参数为λ0.98,0.9,β0.95，迭代次数L20。图3给出了各方法对该场景大小为20 km×20.5 km(方位向×距离向)的成像结果，图3(a)—图3(d)分别对应ωK,MIAA-MCR,IFDM-FISTA和IFDMFISTA-SF方法。表4列出了ωK,MIAA-MCR、使用NUDFT实现的IFDM-FISTA和IFDMFISTA/IFDM-FISTA-SF方法的计算复杂度，其中Md为MIAA-MCR处理时对一个方位向数据的分段长度。由于log2(MN)≪M+(如图3实验中，MN4096,Md100,log2(MN)24,10000,M+N8192)，因此IFDM-FISTA/IFDM-FISTA-SF的计算复杂度要远远小于MIAAMCR和利用NUDFT实现的IFDM-FISTA。表4中IFDM-FISTA/IFDM-FISTA-SF成像处理时间远小于MIAA-MCR和利用NUDFT实现的IFDMFISTA，同样说明了IFDM-FISTA/IFDM-FISTASF是一种高效的处理方法。进一步地，为了证明本文方法比MIAA-MCR能更好地抑制面目标中的方位模糊，取图3中“区域1”和“区域2”进行以下分析。

表4 各方法计算复杂度以及处理图3对应宽幅场景耗时Tab.4 Different methods’ computation complexity and time for the scene given by Fig.3

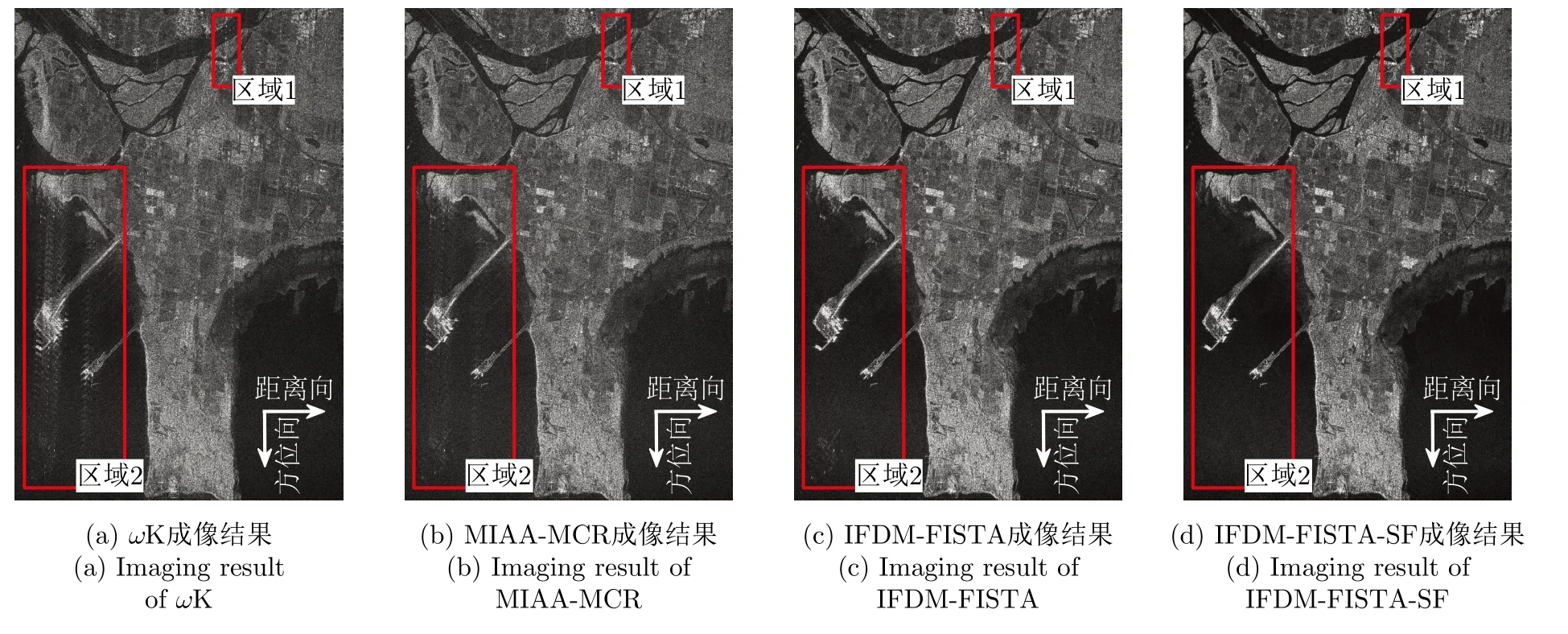
图3 覆盖范围为20 km×20.5 km场景的模拟回波数据处理结果Fig.3 Imaging result of the simulated data of the 20 km×20.5 km scene

图3所示20 km×20.5 km场景中“区域1”的大小为2.8 km×0.8 km(方位向×距离向)。图4(a)—图4(c)分别给出了ωK,MIAA-MCR和IFDM-FISTASF方法对图3“区域1”成像结果的放大图，图4(d)给出了沿着其中强点状目标模糊分布方向的剖面图对比。如图4(a)和图4(b)所示，ωK方法直接成像结果中强点目标的方位模糊十分显著，MIAA-MCR方法成像结果中强点目标的方位模糊相对ωK方法有所减弱，但仍较为显著，这是因为MIAA受面目标谱不稀疏的限制，对面目标回波丢失的恢复性能比对孤立点目标的恢复性能要差；从图4(c)可以发现，IFDM-FISTA-SF方法具有最好的模糊抑制性能；图4(d)所示方位剖面图进一步表明MIAAMCR方法对非稀疏场景中强点的模糊抑制效果虽然要好于ωK，但远差于IFDM-FISTA-SF方法。

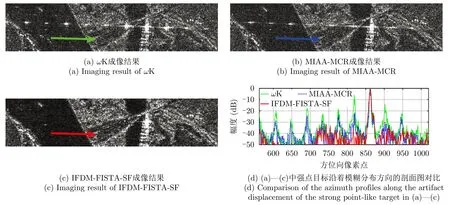
图4 20 km×20.5 km场景中“区域1”成像结果放大图及剖面图对比Fig.4 Larger image of imaging result of“Zone 1”in the 20 km×20.5 km scene and comparison of azimuth profiles

为了体现IFDM-FISTA-SF方法对非理想AAP方位模糊的抑制性能，选取图3所示20 km×20.5 km场景中“区域2”进行分析，其大小为12 km×6 km(方位向×距离向)。图5(a)—图5(d)分别给出了ωK,MIAA-MCR,IFDM-FISTA和IFDM-FISTASF方法对图3“区域2”成像结果的放大图。表5给出了“区域 2”中红色圈内AAP模糊相对于真实目标的ATR值。图5(a)表明ωK直接成像的结果中出现了由回波丢失、非均匀采样以及非理想AAP造成的严重的方位模糊；图5(b)表明MIAA-MCR方法能抑制大部分非均匀采样以及丢失造成的方位模糊，只有少量残余，但无法抑制非理想AAP造成的方位模糊；图5(c)和图5(d)表明IFDM-FISTASF方法首先利用IFDM-FISTA成功抑制由回波丢失、非均匀采样造成的方位模糊，再利用SF抑制非理想AAP造成的方位模糊，从而实现方位模糊完全被抑制的低过采样Staggered SAR高质量成像。表5中MIAA-MCR和IFDM-FISTA的ATR值相比ωK基本不变，而IFDM-FISTA-SF相比ωK则降低了12.41 dB，进一步证明了IFDM-FISTASF方法利用SF对非理想AAP造成的方位模糊进行抑制的良好性能。

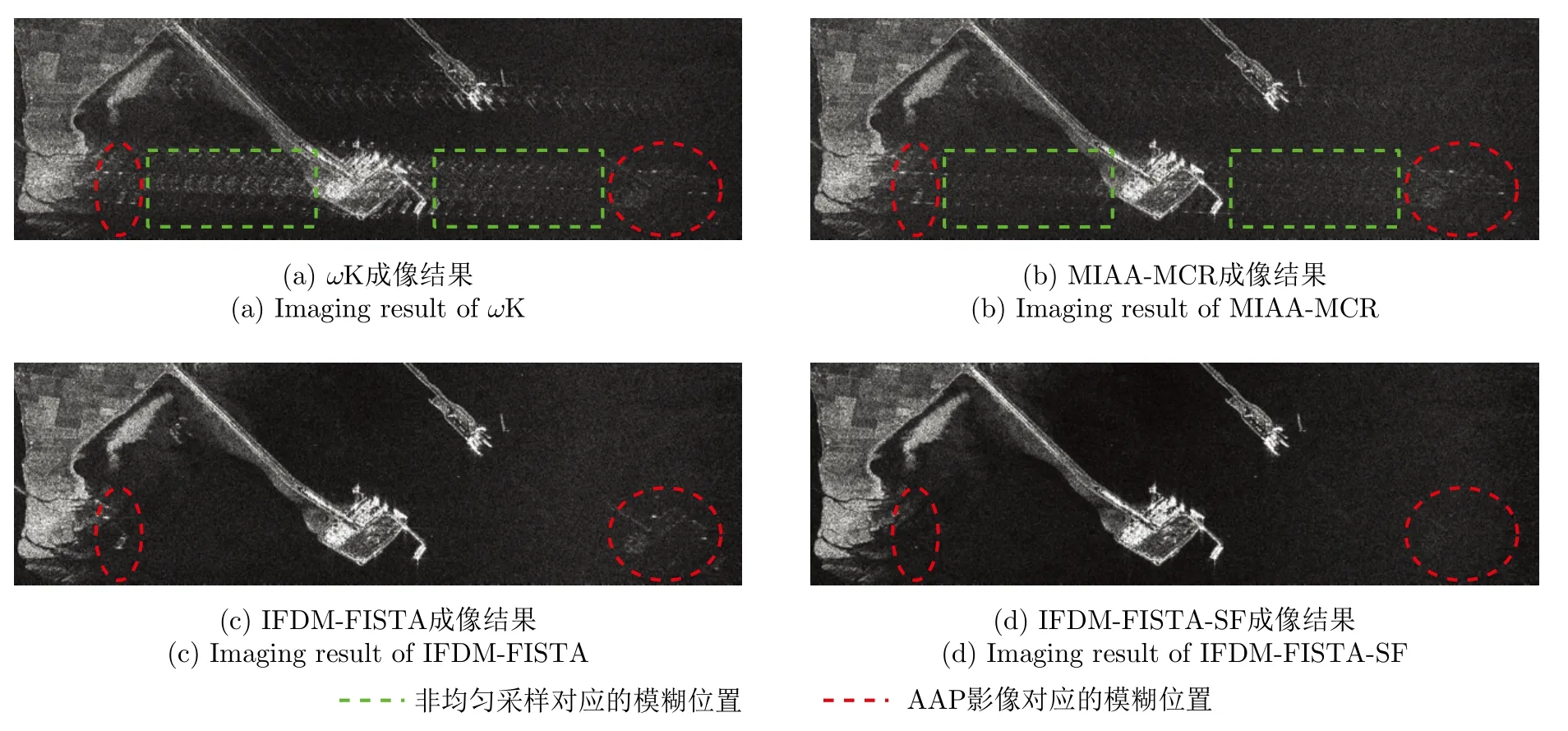
图5 20 km×20.5 km场景中“区域2”成像结果放大图Fig.5 Larger image of reconstructed result of“Zone 2”in the 20 km×20.5 km scene

5 结束语

表5图5(a)—图5(d)中“区域 2”红色圈标注的AAP模糊相对真实目标的ATR结果Tab.5 ATR results corresponding to the AAP ambiguity in red circle of“Zone 2”in Fig.5(a)—Fig.5(d)

针对低过采样Staggered SAR存在的非均匀采样、回波丢失造成的欠采样、RCM和非理想AAP问题，本文提出了一种结合IFDM-FISTA和SF算法的成像方法。实验结果证明了该方法不受非均匀采样、欠采样和非理想AAP问题的影响，可以高效地抑制低过采样Staggered SAR点、面目标成像结果中的方位模糊。与现有谱估计方法处理宽幅场景回波数据相比，本文方法用更少的时间获得了更好的方位模糊抑制效果，证明了本文方法可更加有效且高效地实现高分宽幅成像。此外，该方法逆问题模型IEDM利用三维张量处理RCM，给出了具体的实现过程和清晰的解析解，打破了传统基于匹配滤波CS重建方法必须满足窄带和均匀采样条件的限制，是对传统基于匹配滤波CS重建方法的推广和改进，不但具有理论意义而且更有实用价值。因此，虽然为低过采样Staggered SAR而设计，但通过简单地修改丢失指示矩阵和方位向NUDFT矩阵，本文方法可以扩展应用于采用不同采样方案SAR系统的高质量成像。