水力压裂支撑裂缝导流能力计算与分析

苏映宏 吴忠维 崔传智 陈业祥 马天赐 刘国政

（1. 中国石油化工股份有限公司石油勘探开发研究院， 北京 100083； 2. 中国石油大学（华东） 石油工程学院， 山东青岛 266580）

0 引 言

水力压裂技术已广泛运用于油气藏开发， 而水力压裂能否产生高导流人工裂缝是评价水力压裂效果好坏的关键之一［1-3］。 目前关于水力压裂支撑裂缝导流能力研究较多［4-6］， 可分为运用实验手段与数学理论分析两个方面去研究支撑裂缝导流能力。Lacy 等［7-8］通过室内实验手段， 研究了支撑剂在软地层中的嵌入与嵌入后的导流能力； 并于1998 年研发了一种计算机控制实验技术， 该技术可用于测量裂缝宽度与支撑剂在软地层中的嵌入深度。Fredd 等［9］运用德克萨斯Cotton 砂岩储层岩心展开了一系列的裂缝导流能力实验， 研究结果表明， 在没有支撑剂的情况下， 裂缝不平整与裂缝面的位移导致裂缝闭合不完全， 从而提供足够的裂缝导流能力； 这种情况下导流能力变化在2 个数量级之内，具体的参数值主要受裂缝壁面凹凸大小、 分布及实验硬度等力学性质控制。 对于支撑裂缝的导流能力主要受支撑剂浓度、 支撑剂强度、 地层性质控制。Barree 等［10］运用室内实验手段阐明了支撑裂缝导流能力伤害机理。 王丽伟等［11］运用ZCJ-200 型导流能力试验装置开展了3 种不同压裂液在相同支撑剂类型、 铺置浓度、 不同闭合压力下对支撑剂充填裂缝导流能力的伤害程度研究。 郭建春等［12］运用自行研制的支撑剂嵌入程度测试分析系统研究了支撑剂在地层岩心中的嵌入程度， 并考察了不同铺砂浓度、 不同应力条件对各岩心的支撑剂嵌入情况。 卢聪等［13］运用自行研制的测试仪器， 对地层岩心的支撑剂嵌入情况进行了实验研究， 并在支撑剂嵌入的基础上， 考虑了地层碎屑对裂缝导流能力损害的影响。 曲占庆等［14］运用改进的FCES-100 裂缝导流仪， 研究了支撑裂缝导流能力影响因素作用规律， 并提出了改善支撑裂缝导流能力方法。 以上研究均是通过实验手段去研究支撑剂裂缝导流能力， 这些研究均没有涉及到裂缝导流能力的解析模型， 尤其缺失考虑裂缝形态的导流能力表征方法。

李勇明等［15］运用微元分析方法给出了支撑剂嵌入深度计算模型， 并分析了闭合压力、 支撑剂粒径、 岩石弹性模量对支撑剂嵌入的影响。 孟雅等［16］在分析支撑剂铺置类型的基础上， 运用K-C方程， 建立了考虑支撑剂大小、 铺置层数、 闭合压力等参数影响的裂缝导流能力表征公式， 并分析了这些关键参数的影响； 但这些研究只是适用于平板裂缝情况， 而实际裂缝多成楔形。 赵金洲等［17］、Li 等［18］运用弹性力学理论， 考虑支撑剂变形与嵌入， 建立了单层、 多层支撑剂铺置类型下的裂缝导流能力计算方法， 并通过与实验结果对比验证了模型的准确性， 他们的研究结果复杂， 不便于现场运用且所运用的弹性理论方程并不完全适用于支撑剂嵌入裂缝过程。 张遂安等［19］根据Hertz 理论， 推导出二维多层支撑剂嵌入煤岩的缝宽模型和压嵌模型， 利用实验数据对模型进行了验证。 陈铭等［20］建立了支撑剂嵌入岩体的本构方程， 再结合岩体—支撑剂体系的接触应力分析， 提出了弹塑性变形的支撑剂嵌入深度计算方法。

基于以上分析可知， 目前缺少考虑裂缝形态（楔形） 与支撑剂嵌入的支撑裂缝导流能力计算方法。 因此， 在考虑支撑剂嵌入、 裂缝形态影响的基础上， 建立了支撑裂缝导流能力计算模型， 并分析了关键参数对裂缝导流能力的影响， 该研究对水力压裂设计与优化具有重要意义。

1 支撑裂缝导流能力计算模型

水力压裂在储层中形成了裂缝宽度不等的楔形支撑裂缝（裂缝宽度沿着裂缝方向远离井筒线性降低）， 为解决裂缝宽度变化对支撑裂缝导流能力计算的难度， 将裂缝沿缝长离散成多个裂缝微元，每个裂缝微元的裂缝宽度不变， 但裂缝微元之间的裂缝宽度不同。 通过计算每个离散微元的导流能力， 最后可获得整个裂缝的导流能力。

由于在储层应力作用下裂缝闭合、 支撑剂嵌入储层， 因此支撑裂缝导流能力计算模型分为2 部分， 分别为不考虑支撑剂嵌入的支撑裂缝导流能力计算与考虑支撑剂嵌入的支撑裂缝导流能力计算。

1.1 不考虑支撑剂嵌入的支撑裂缝导流能力计算

支撑剂在裂缝中的铺置类型包括单层铺置与空间铺置， 其中单层铺置包括正对铺置与交错铺置［21］。 选取单层铺置类型中的交错铺置类型开展研究， 图1 为支撑剂交错铺置的示意。

裂缝离散成多个微元后， 每个裂缝微元的导流能力计算方法相同， 以裂缝跟端（裂缝入口处）微元为例， 介绍裂缝微元的导流能力计算方法。

针对裂缝跟端微元， 依据支撑剂铺置类型， 可以获得几何关系： ①裂缝宽度等于wfr与2R之和，其中wfr表示的长度见图2，R为支撑剂颗粒半径；②wfr为n-1 倍的WFR，n为支撑剂层数，WFR表示的长度见图2。

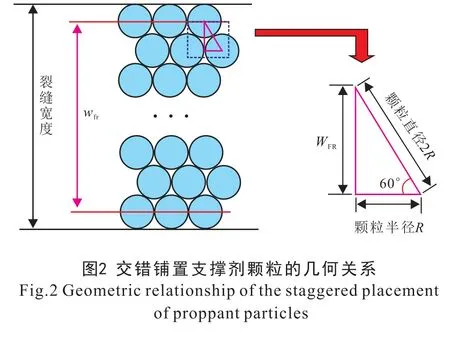
将几何关系②代入①中， 可得裂缝跟端宽度与铺置层数、 支撑剂大小的关系为

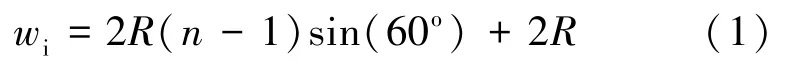
式中：wi——裂缝跟端宽度， m；R——支撑剂半径， m；n——支撑剂层数。

将式（1） 变形， 可以获得支撑剂层数计算公式为

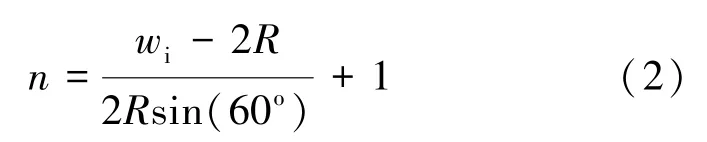
取裂缝长为lfΔ单元（裂缝宽度为wi、 裂缝高度为h）， 依据孔隙度定义（该单元中孔隙体积与外表体积之比）， 可得裂缝跟端孔隙度计算公式为

又有表征渗透率与孔隙度、 孔隙半径关系的Kozeny-Carman 方程， 即

式中：K——渗透率， μm2；r——有效流动孔隙半径， μm；τ——有效流动孔隙的迂曲度；φ——孔隙度。

将式（3） 代入方程式（4）， 可以得到裂缝跟端渗透率公式

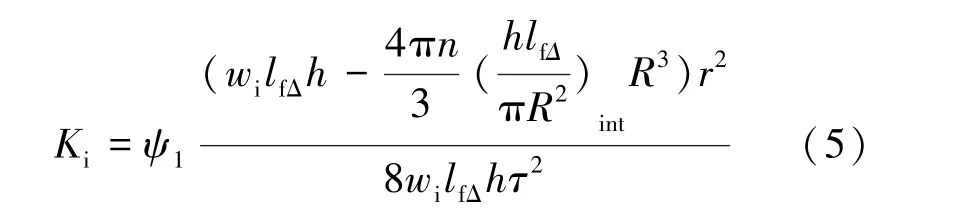
式中：Ki——裂缝跟端渗透率， μm2；ψ1——单位转换系数， 取值为1012。

从式（5） 可知， 若要求取裂缝跟端渗透率，必须取半径r。 以下通过分析支撑剂铺置类型， 求取有效流动孔隙半径r。 通过支撑剂铺置类型， 可知支撑裂缝有效流动孔隙可以分为2 种： 由支撑剂环绕形成的孔隙（即不与裂缝壁面接触的孔隙）与由支撑剂和裂缝环绕而成的孔隙（即与裂缝接触的孔隙）。 图3 为不与裂缝壁面接触的孔隙示意； 由图3 可知， 有效流动孔隙由多个支撑剂围绕而成。

针对不与裂缝壁面接触孔隙， 运用高度为颗粒直径大小的三菱柱去截（见图3 中的三角形），再依据体积守恒可知： 三菱柱体积等于孔隙体积与支撑剂颗粒所占体积之和。 依据该关系并运用体积守恒将孔隙等效为圆柱， 可以获得不与裂缝接触孔隙的有效半径与支撑剂半径的关系为

式中rff1——不与裂缝接触孔隙的有效半径， m。

将式（6） 变形， 可以获得不与裂缝接触孔隙的有效半径rff1为

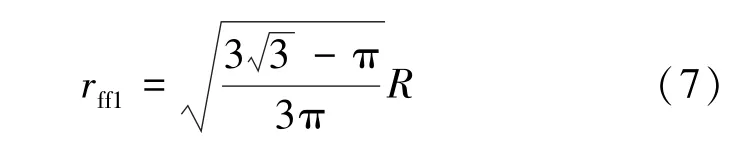
对于与裂缝接触的有效流动孔隙（图4） 可知， 孔隙由裂缝壁面与支撑剂围绕而成。

运用高度为颗粒直径大小的长方体去截（图4）， 依据体积守恒可得： 长方体体积等于孔隙体积与支撑剂所占体积之和。 依据该关系并运用体积守恒将孔隙等效为圆柱， 可得与裂缝接触孔隙的有效半径与支撑剂半径的关系为

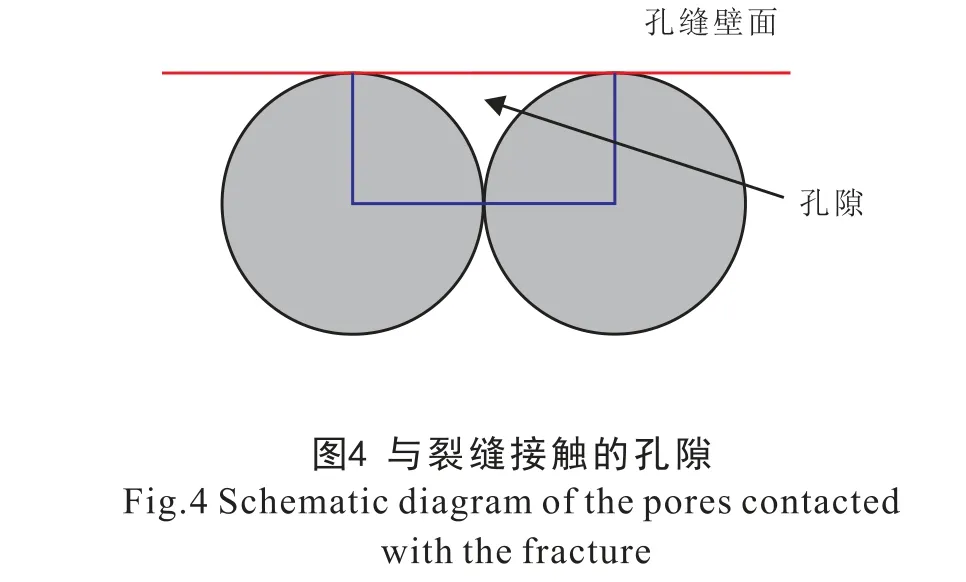
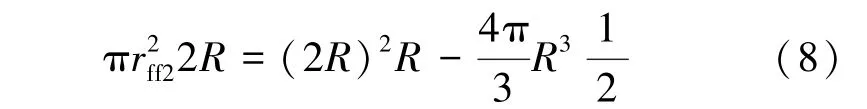
式中rff2——与裂缝接触的孔隙半径， m。

将式（8） 变形， 可以获得与裂缝接触的孔隙半径rff2为

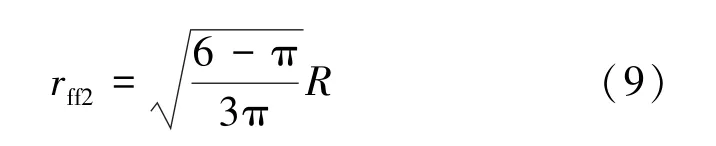
依据支撑剂铺置类型可知： 对于n层裂缝， 有2n个有效流动孔隙； 其中（2n-2） 个不与裂缝接触的有效流动孔隙， 2 个与裂缝接触的有效流动孔隙。 依据孔隙个数平均， 可获得平均孔隙半径为

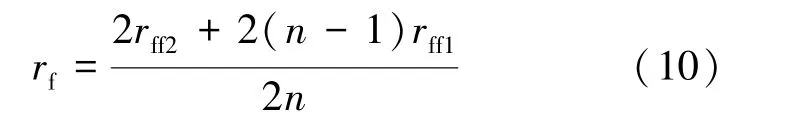
式中rf——等效后的平均孔隙半径， m。

将式（10） 代入式（5） 可以获得支撑裂缝跟端绝对渗透率。 由于压裂液残留、 支撑剂破碎、 裂缝壁面凹凸不平等都将伤害支撑裂缝渗透率， 故引入伤害系数ϑ， 修正裂缝绝对渗透率为

式中ϑ——渗透率伤害系数， 该系数描述了压裂液残留、 支撑剂破碎、 裂缝避免凹凸不平等对渗透率的伤害， 通过与实验结果对比， 确定该参数的取值。

将式（11） 乘以裂缝跟端宽度即得裂缝跟端的导流能力。 针对其他离散的裂缝微元， 运用以上方法， 可以求得其渗透率与裂缝导流能力， 最后可以获得不考虑支撑剂嵌入的、 沿裂缝长度分布的导流能力。

1.2 考虑支撑剂嵌入的支撑裂缝导流能力计算

受裂缝闭合应力影响， 支撑剂将嵌入裂缝。 先计算支撑剂嵌入深度， 再通过修正不考虑支撑剂嵌入的支撑剂裂缝导流能力计算公式， 获得考虑支撑剂嵌入时的导流能力计算公式。

1.2.1 支撑剂嵌入深度计算与分析

由图5 可知， 支撑剂嵌入裂缝壁面后存在以下三角关系， 即

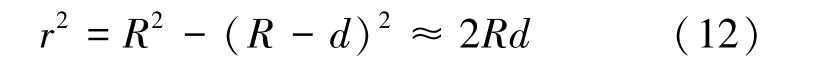
式中：r——与壁面接触面积在裂缝壁面上投影圆的半径， m；d——支撑剂嵌入裂缝壁面深度， m。

又有与壁面接触面积在裂缝壁面上投影圆的面积公式， 即

将式（12） 代入到式（13） 中， 可得投影圆面积为

对支撑剂进行受力分析， 依据受力平衡关系可得

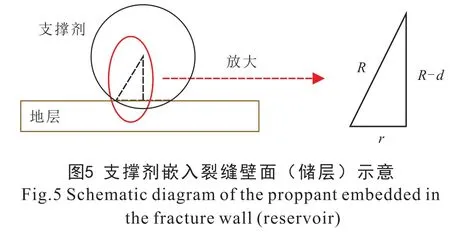
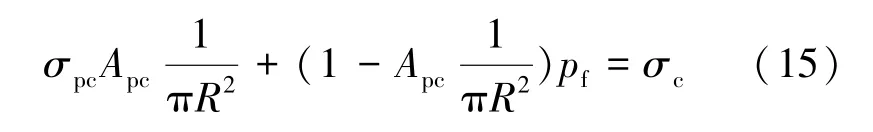
式中：σpc——接触面平均接触应力， Pa；pf——裂缝流体所受压力， Pa；σc——裂缝闭合应力， Pa。

依据Hertz 理论， 支撑剂嵌入深度d与平均接触应力σpc存在关系

运用式（14）、 式（15）、 式（16） 可以获得嵌入深度的隐式表达式

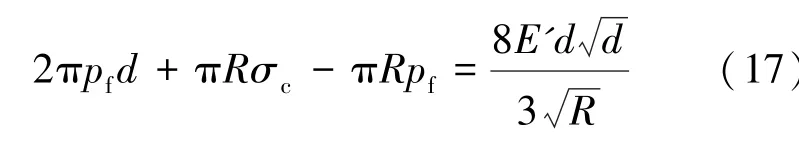
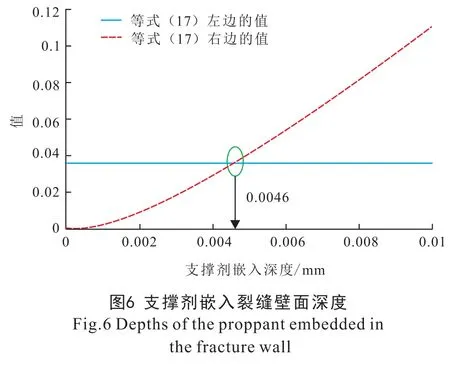
由于嵌入深度公式为隐式公式， 本文采用图解法获取支撑剂嵌入深度， 计算所用数据见表1， 计算结果见图6。 由图6 可知， 式（17） 右边的值连续增加， 而左边的值相对比较平缓； 两条线相交于0.004 6 mm； 即当岩石与支撑剂的弹性模量分别为35 210、 41 306 MPa 时， 支撑剂的嵌入深度小于支撑剂半径（只有半径的1.9%）， 嵌入深度极小。

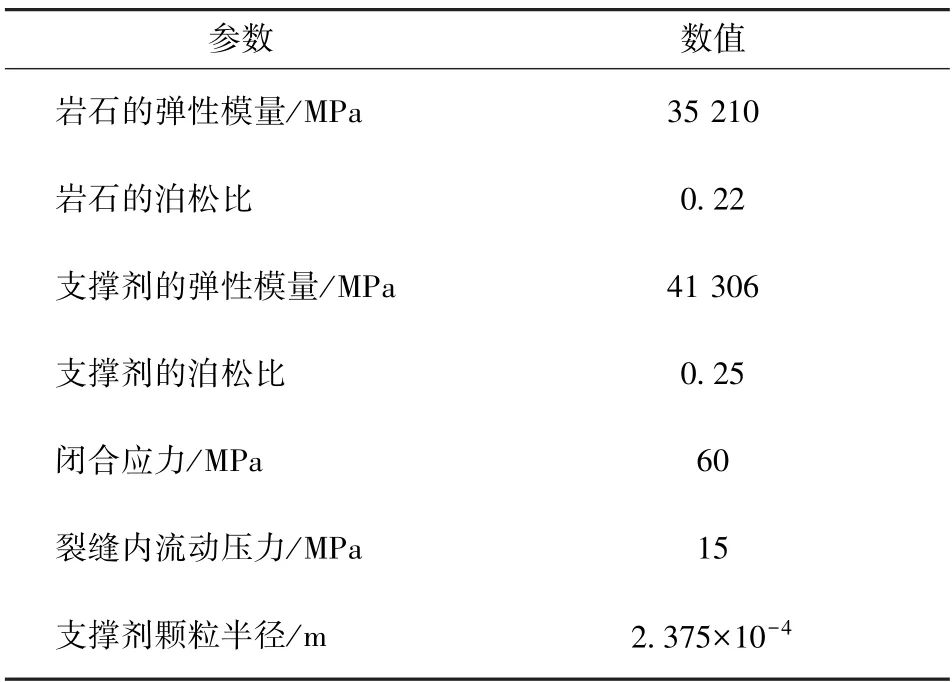
表1 支撑剂嵌入裂缝壁面深度计算所需参数Table 1 Parameters required for calculating the depth of the proppant embedded in the fracture wall

1.2.2 支撑裂缝的导流能力

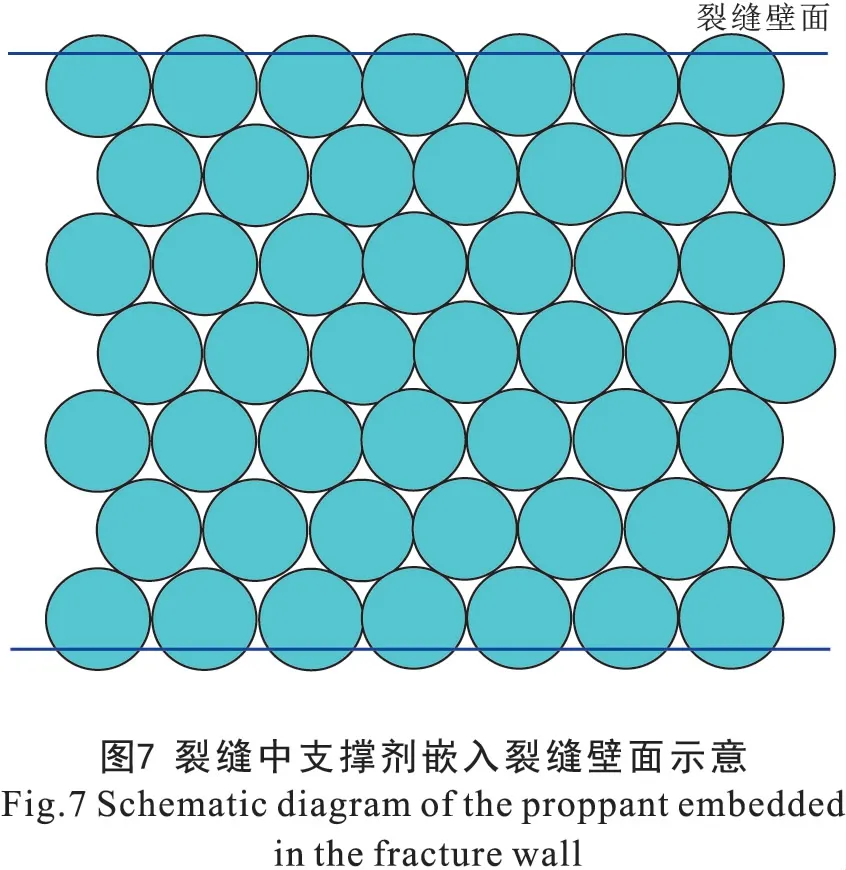
由于支撑剂嵌入深度小于支撑剂半径， 故得裂缝中支撑剂嵌入裂缝壁面示意（图7）。 由图7 可知， 支撑剂嵌入主要改变与裂缝接触孔隙的流动空间， 由于嵌入深度极小， 且与裂缝接触流动孔隙数占总孔隙数比例很小， 所以忽略对有效流动孔隙半径的影响； 故只需修正不考虑支撑剂嵌入深度导流能力计算公式中的孔隙度， 就可获得考虑支撑剂嵌入的支撑裂缝导流能力计算公式。 由于每个离散的裂缝微元计算方法相同， 所以以裂缝跟端为例介绍考虑支撑剂嵌入的支撑裂缝导流能力计算方法。

支撑剂嵌入之后， 裂缝跟端孔隙度计算公式为

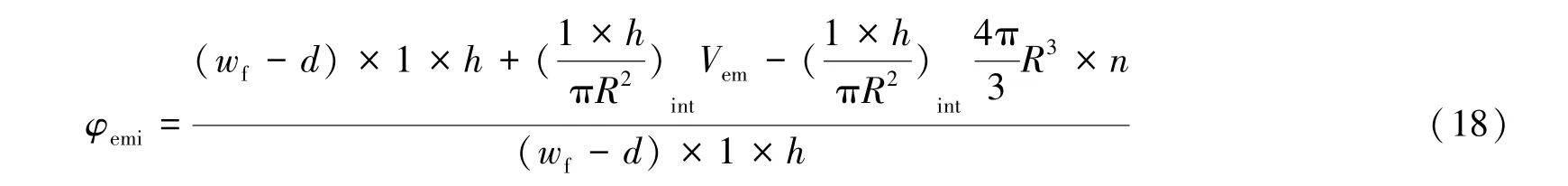
式中：φemi—— 嵌入之后的支撑裂缝孔隙度；

Vem——支撑剂嵌入裂缝壁面的体积， m3。

由于嵌入深度d相比于支撑剂半径较小， 故可以将式（18） 简化为

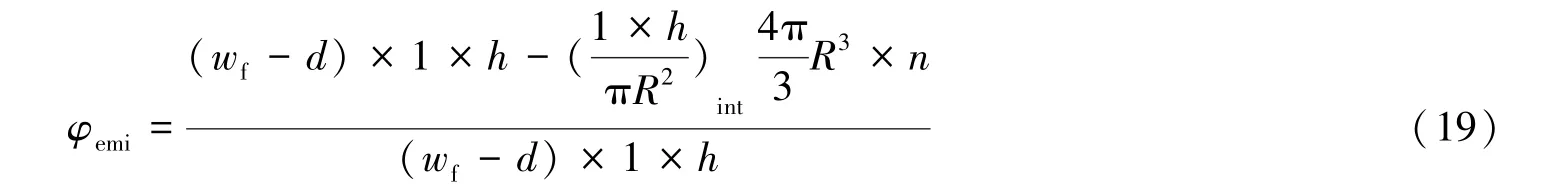
依据Kozeny-Carman 公式， 并引入渗透率伤害系数ϑ， 以考虑压裂液残留、 支撑剂破碎、 裂缝避免凹凸不平等对渗透率的伤害， 可以获得嵌入后裂缝的渗透率计算公式为

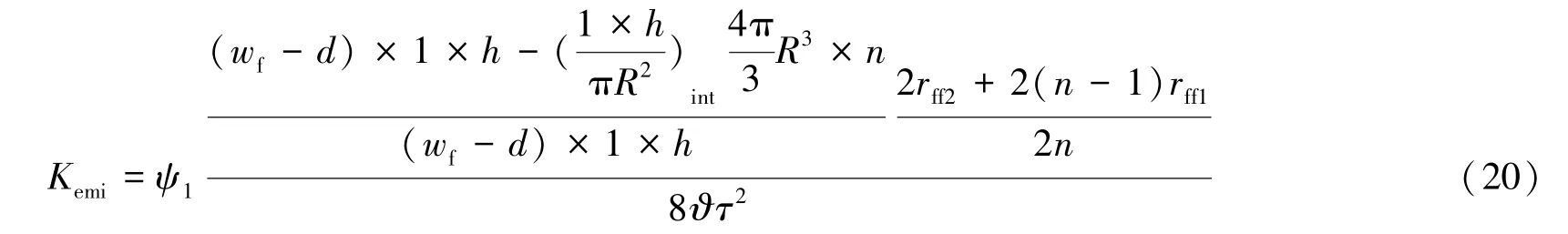
式中Kemi——考虑嵌入之后的支撑裂缝跟端渗透率， μm2。

将式（20） 乘以裂缝跟端宽度即得裂缝跟端的导流能力。 针对其他离散的裂缝微元， 运用以上方法， 可以求得其渗透率与裂缝导流能力； 最后可以获得考虑支撑剂嵌入的沿裂缝分布的导流能力。

2 裂缝导流能力计算模型验证与影响因素

2.1 导流能力计算模型验证

为验证支撑裂缝导流能力计算模型的准确性，简化本文模型， 运用简化模型去计算任一宽度、 支撑剂大小条件下的填充裂缝导流能力， 并将计算结果与文献［13］ 中的报道结果进行对比。 模型验证所用的参数见文献［13］， 对比结果见表2。 从表2 中可知， 本文模型与文献［13］ 中报道结果很相近， 相对误差最大为5.05%。 该对比说明了本文模型能用于准确计算支撑裂缝导流能力。

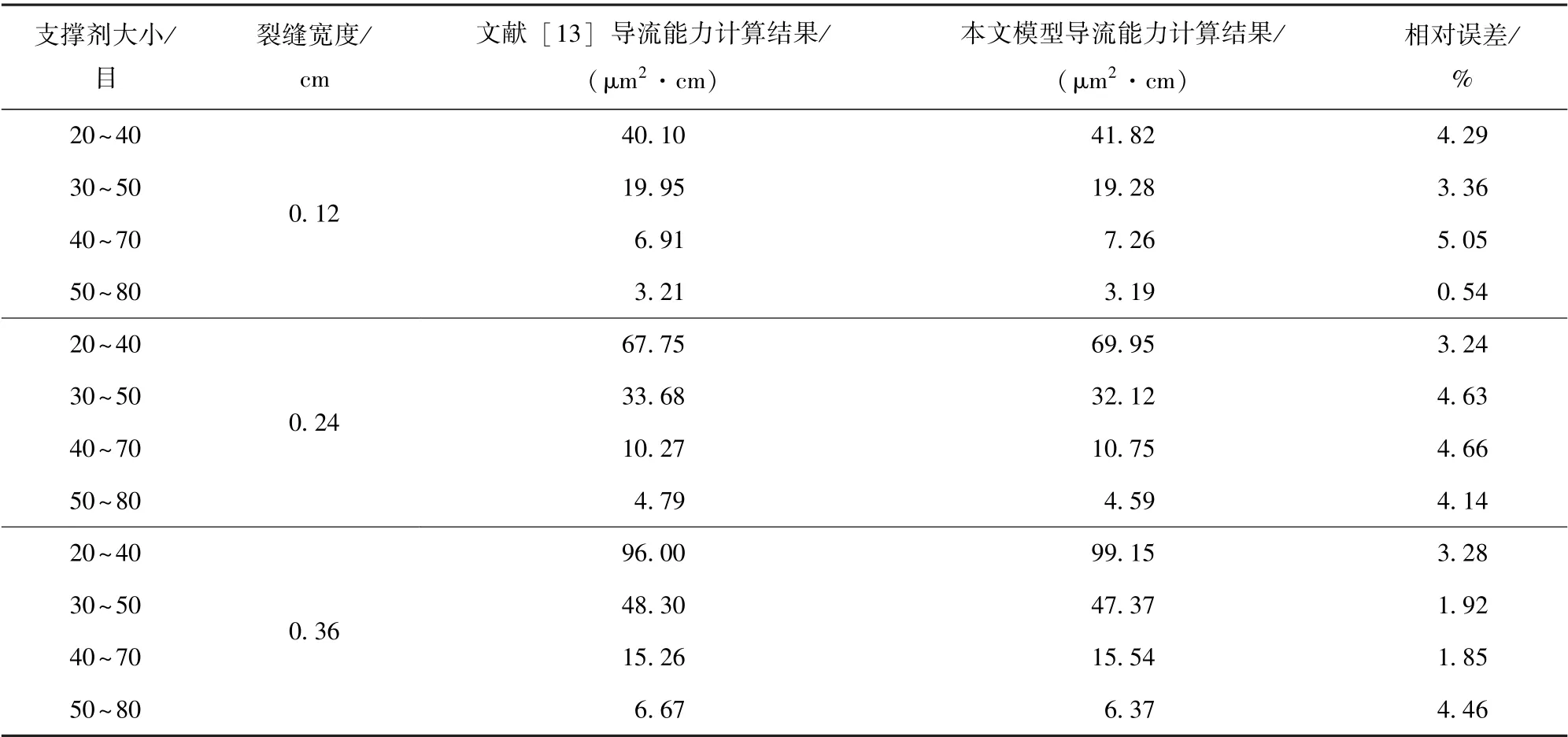
表2 本文模型计算结果与文献［13］ 结果对比Table 2 Comparisons between the results calculated by the model and Literature ［13］

2.2 导流能力关键参数的影响规律

影响因素分析所用的参数分别为： 裂缝跟端宽度0.002 m， 裂缝长度100 m。由于支撑剂的常用单位为目， 为方便计算， 获得单位目与单位米之间的换算关系， 具体见表3。

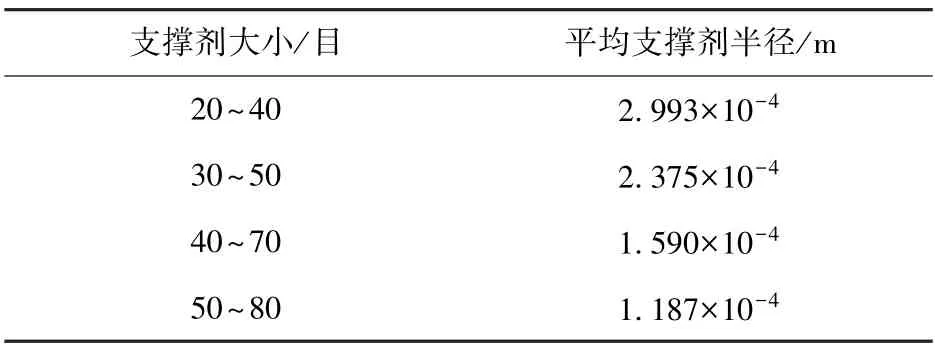
表3 支撑剂目数与支撑剂半径对应关系［13］Table 3 Correspondences between the proppant mesh number and proppant radius［13］

2.2.1 支撑剂半径对裂缝导流能力的影响

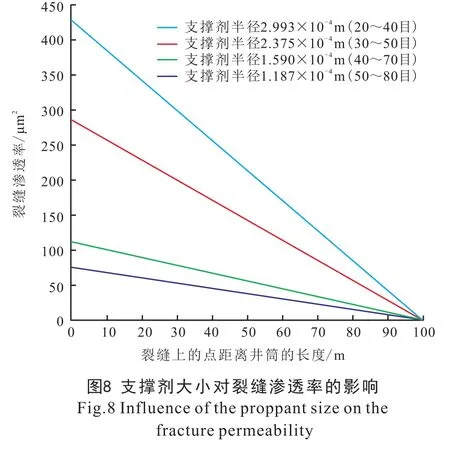
运用以上参数与建立的模型，分析支撑剂半径对支撑裂缝渗透率与导流能力的影响。 由图8 可知，在支撑剂大小不变的情况下， 沿着裂缝， 离井筒越远， 裂缝渗透率降低； 这是由于沿着裂缝远离井筒， 裂缝宽度越来越小， 导致渗透率降低。 在裂缝宽度不变的情况下， 即在裂缝跟端处， 随着支撑剂半径越大， 裂缝渗透率越高。 这是由于在裂缝宽度一定的情况下， 支撑剂半径越大， 有效流动孔隙半径越大， 因而渗透率越大。

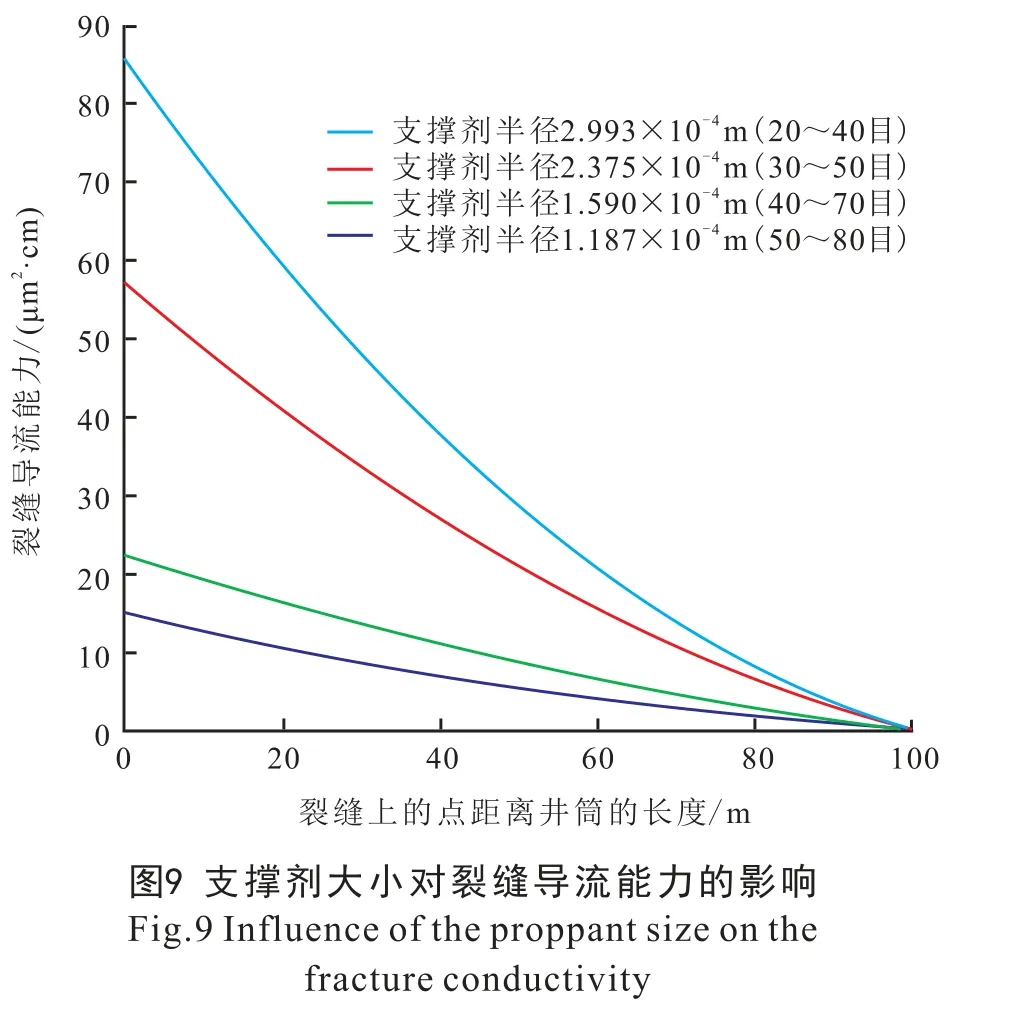
由图9 可知， 当支撑剂大小一定时， 沿着裂缝远离井筒， 导流能力降低， 且降低速度由大变小； 这是因为沿着裂缝远离井筒， 裂缝宽度越来越小， 同时渗透率也越小， 因此导流能力越来越小。当裂缝宽度不变时， 随着支撑剂半径增加， 裂缝导流能力增加； 这是由于裂缝宽度不变时， 支撑剂半径越大， 导致裂缝渗透率越大， 因此裂缝导流能力越大。

2.2.2 裂缝跟端宽度对裂缝导流能力的影响

支撑剂大小为20 ～40 目 （即支撑剂半径为2.993×10-4m）， 其他参数见前所述， 分析裂缝跟端宽度对裂缝跟端渗透率、 导流能力的影响。 由图10 可知， 当裂缝跟端宽度一定时， 沿着裂缝远离井筒， 渗透率越小； 这是由于沿着裂缝远离井筒，裂缝宽度越小， 在支撑剂大小一定的条件下， 裂缝渗透率越小。 当支撑剂大小一定时， 裂缝跟端宽度增加， 导致裂缝跟端渗透率增加， 且增加的速度先快后慢。 这是由于支撑剂大小一定， 裂缝跟端宽度越大， 渗透率越大； 且裂缝宽度越大， 支撑剂层数越多； 使得与裂缝接触孔隙半径占比越小， 由于与裂缝接触孔隙半径小于不与裂缝接触孔隙半径， 因此等效半径越大， 这样也导致渗透率的增加。 当裂缝跟端宽度从小到大时， 与裂缝接触孔隙半径占比变小， 且变小速度从快到慢， 故渗透率增加速度从大到小。

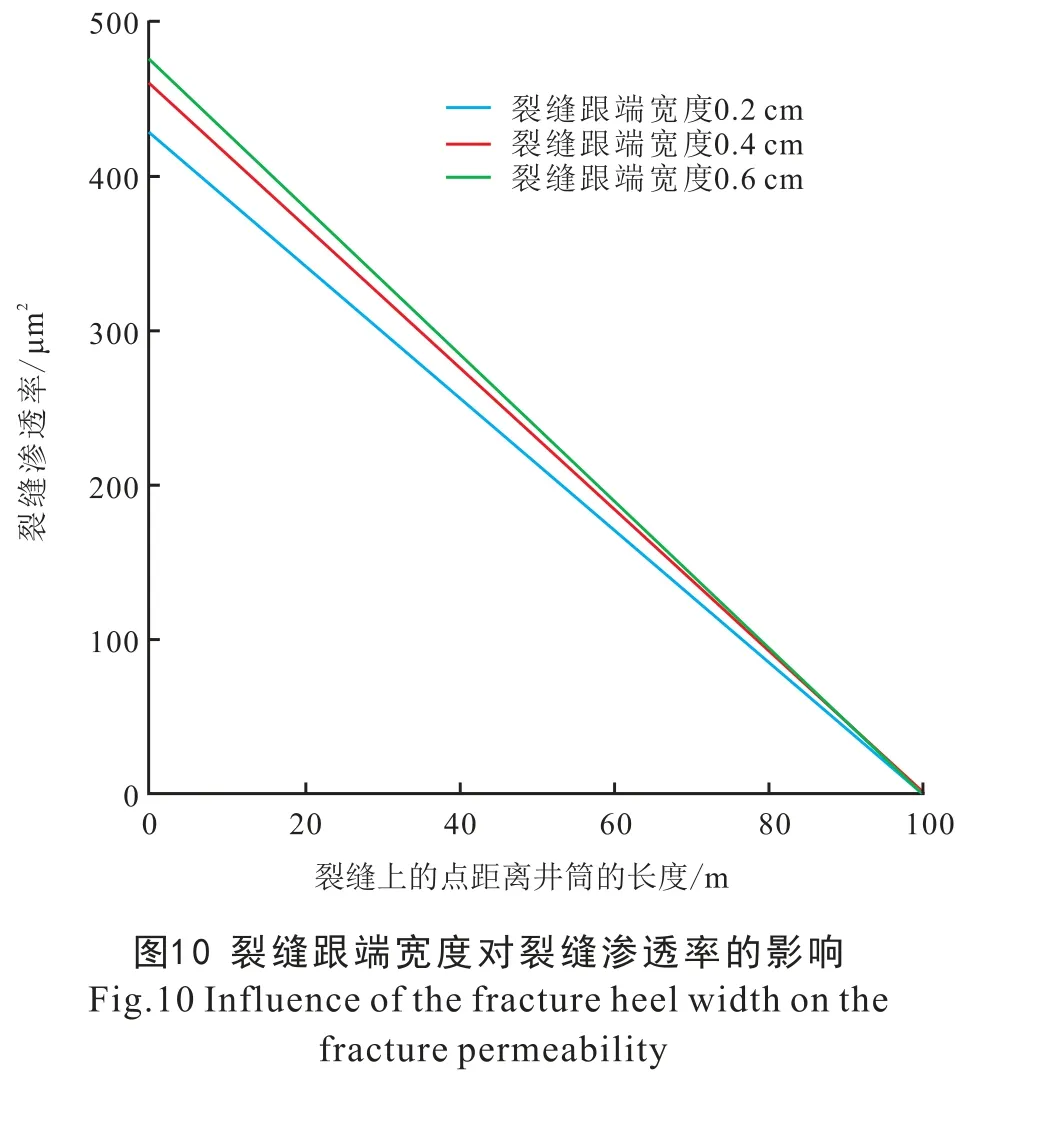
由图11 可知， 当裂缝跟端宽度、 支撑剂大小一定时， 沿着裂缝远离井筒， 裂缝导流能力越来越小， 且降低的速度从快到慢。 这是由于沿着裂缝远离井筒， 裂缝宽度降低， 渗透率也降低， 故裂缝导流能力降低。 当支撑剂大小一定时， 裂缝跟端宽度越大， 裂缝跟端的导流能力越大。 这是由于裂缝跟端宽度越大， 裂缝跟端渗透率越大， 故跟端导流能力越大； 同时跟端宽度越大， 支撑剂层数越多， 与裂缝接触的孔隙半径占比越小， 由于与裂缝接触孔隙半径小于不与裂缝接触孔隙半径， 故裂缝渗透率进一步增加。

2.2.3 支撑剂嵌入对导流能力的影响

图12 为支撑剂嵌入对导流能力的影响。 由图12 （a） 可知， 支撑剂跟端宽度越大， 裂缝导流能力越大； 沿着裂缝远离井筒， 裂缝导流能力降低。与支撑剂不嵌入的情况相比， 各裂缝跟端宽度下的支撑剂嵌入后裂缝导流能力均小于不考虑嵌入时的裂缝导流能力； 且沿着裂缝远离井筒， 嵌入与不嵌入的导流能力绝对差值从大变小。 这是由于当支撑剂嵌入裂缝壁面时， 相当于有效裂缝宽度变小同时单位体积内的有效流动孔隙也变小， 故裂缝导流能力降低。 图12 （b） 为不同的支撑剂大小情况下，支撑剂嵌入与不嵌入对沿着裂缝方向的裂缝导流能力的影响。 支撑剂目数越小， 即支撑剂半径越大时， 裂缝导流能力越大； 且与支撑剂不嵌入相比，支撑剂嵌入时的裂缝导流能力要小于不嵌入情况的裂缝导流能力； 沿着裂缝远离井筒， 支撑剂嵌入对裂缝导流能力的影响变小。 这是由于裂缝嵌入降低了有效裂缝宽度， 同时也降低了单位体积内的有效流动孔隙。 当裂缝宽度较小（0.2 cm）、 支撑剂半径较小（50 ～70 目） 时， 嵌入对裂缝导流能力的影响较弱。

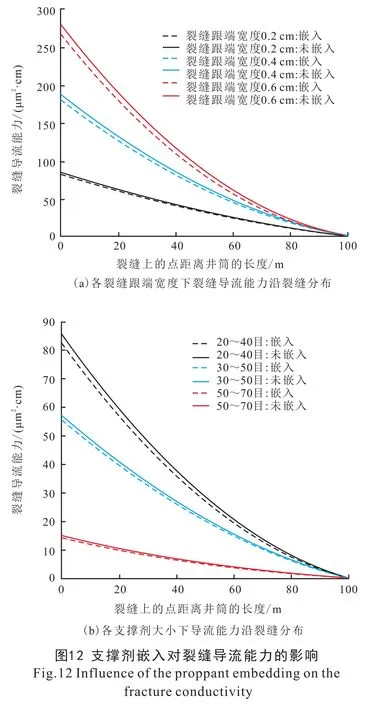
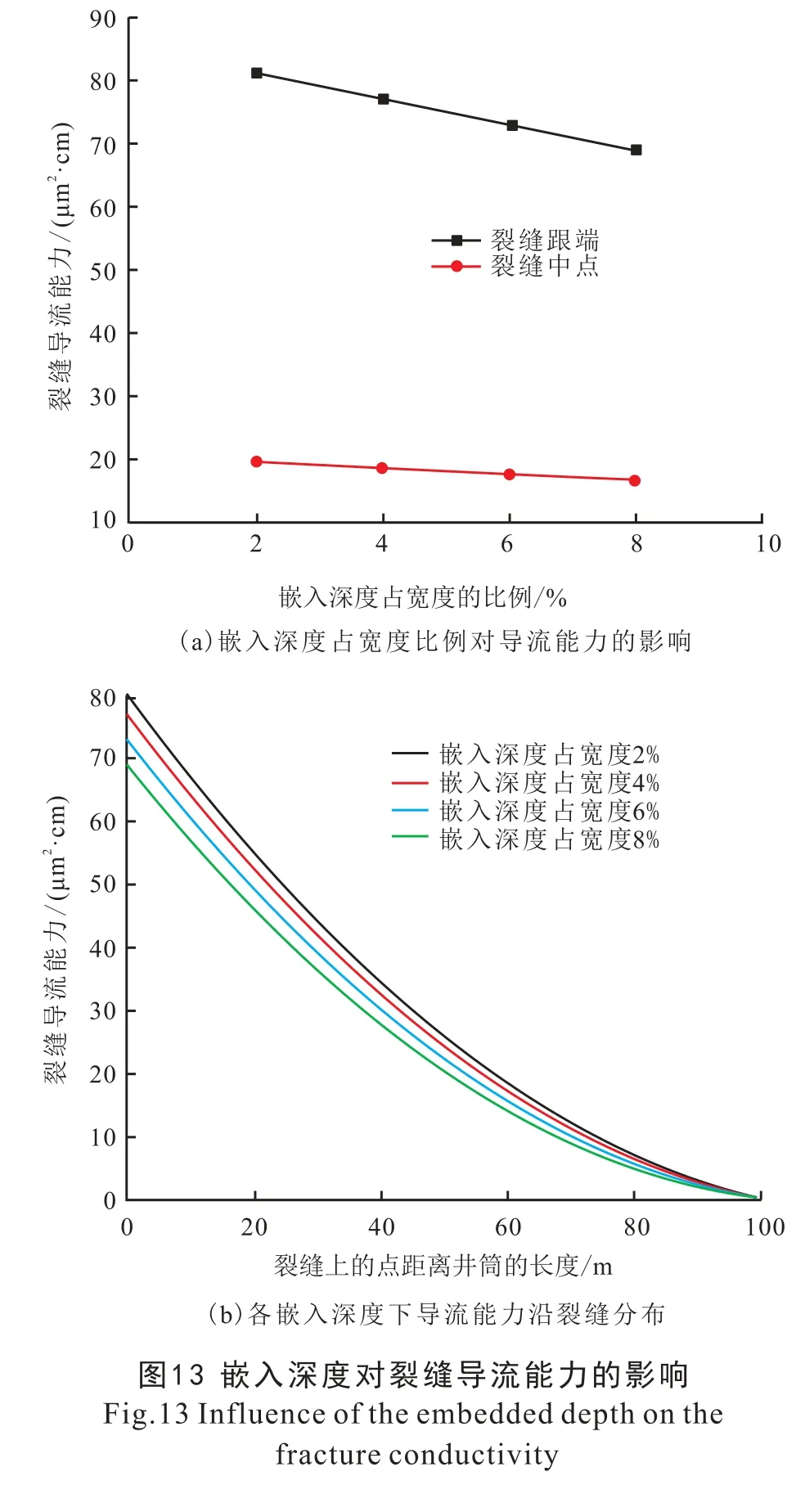
图13 为嵌入深度对裂缝导流能力的影响。 由图13 （a） 可知， 裂缝嵌入深度占裂缝宽度比例越大， 裂缝跟端与中点处的导流能力越小。 这是由于随着裂缝嵌入深度占裂缝宽度比例变大， 有效流动孔隙越少， 单位体积的流动孔隙越小， 依据K—C方程， 可得其渗透率越小； 故裂缝跟端与中点处裂缝导流能力越低。 图13 （b） 为不同支撑剂嵌入深度下， 沿着裂缝分布的导流能力。 当支撑剂嵌入深度不变时， 沿着裂缝远离井筒， 裂缝导流能力降低， 且降低速度由快变慢； 当裂缝位置不变时， 裂缝嵌入深度越大， 裂缝导流能力越小。 这是由于沿着裂缝远离井筒， 裂缝宽度越来越小， 渗透率也越来越小， 故导流能力降低。 当裂缝位置不变时， 裂缝宽度不变； 由于支撑剂嵌入深度将导致有效宽度减小； 嵌入深度越大， 有效宽度越小； 故最终使得支撑剂嵌入深度与裂缝导流能力呈现出支撑剂嵌入深度越大， 导流能力越小的特征。

3 结 论

（1） 建立了考虑支撑剂嵌入的楔形支撑裂缝导流能力计算模型， 并通过与已报道的支撑裂缝导流能力进行对比， 验证了模型的准确性。 该模型说明了支撑裂缝导流能力与支撑剂大小、 支撑剂嵌入、 裂缝宽度等参数有关， 其能用于计算沿裂缝分布的导流能力。

（2） 沿着裂缝远离井筒， 裂缝渗透率降低，导流能力降低； 但导流能力降低趋势为先降低快、后降低慢。 裂缝支撑剂大小不变条件下， 裂缝宽度越大， 裂缝渗透率越大； 裂缝宽度越大， 导流能力越大； 裂缝宽度一定时， 支撑剂半径越大， 渗透率与导流能力越大。

（3） 当岩石与支撑剂的弹性模量分别为35 210、41 306 MPa 时， 支撑剂的嵌入只有支撑剂半径的1.9%， 嵌入深度极小； 支撑剂嵌入后裂缝导流能力沿着裂缝变化的趋势与支撑剂嵌入前相同； 但支撑剂嵌入后的裂缝导流能力与嵌入前的情况相比有所下降。 支撑剂直径越小或嵌入深度越大， 裂缝中有效流动空间变小， 最终导致裂缝导流能力的降低。