铝合金桁架桥梁大偏心节点连接受力性能分析与设计优化
2022-01-07温庆杰许原浩任子健
温庆杰 许原浩 任子健
(中国矿业大学力学与土木工程学院,徐州 221116)
0 引言
铝合金材料具有轻质高强、耐腐蚀、耐久性好等诸多优点,在桥梁工程中尤其是人行天桥领域得到大量应用[1-2]。在实际工程中由于构造要求和安装误差等因素,可能导致桁架桥梁的节点处各连接构件的截面中心不交于一点,处于偏心状态,而偏心节点连接会在各连接构件上产生较大的次内力,从而降低节点连接的刚度和承载力,导致桁架结构整体受力性能劣于非偏心结构[3-6]。因此针对节点处构件偏心连接时结构受力性能和节点构造设计进行研究尤为重要。目前对钢结构连接节点的研究已取得众多研究成果,倪宋健[7]通过计算次正应力比来分析节点刚性和节点偏心引起的次应力对结构的影响,发现节点刚性和节点偏心引起次应力的影响在不同的位置是不同的;李会军等[8]提出考虑随机杆件偏心的力学模型和数值计算方法,深入研究了连接杆件对节点的偏心缺陷对网壳稳定承载力的影响程度,发现杆件偏心越大,网壳结构的极限荷载越小,承载力的离散性越大;施正捷[9]研究发现偏心钢结构节点的刚度相对于非偏心节点有较大程度的削弱,偏心节点核心区引起的梁端变形中扭转分量占主要部分,提出了偏心钢节点剪切屈服形态下的承载力计算公式。在工程设计中,较大的构件连接偏心距对钢结构节点及整体受力性能的影响不容忽视,《钢结构设计标准》[10]规定,在钢管结构中,当节点偏心距e与连接平面内弦杆截面高度h的比值小于-0.55或大于0.25时,必须考虑因偏心引起的次弯矩的影响。但由于铝合金材料的力学性能不同于钢材,大节点偏心作用下受力性能可能存在较大差别,而相关文献很少。孟雨泽等[11]通过建立共节点和不共节点的有限元模型对偏心连接下铝合金人行天桥桁架节点的受力特性进行研究,发现两个模型计算结果相近且都满足规范设计要求。但是其研究对象的构件节点连接偏心距很小,很有必要对大节点偏心作用下的结构受力开展研究。
本文以一座大偏心节点连接的铝合金人行桁架桥为研究对象,采用有限元模拟和理论计算方法,分别建立理想铰接模型和考虑节点偏心模型,研究桁架构件大偏心节点连接时构件的次弯矩及结构变形和应力,并分析桁架节点连接的承载力,提出设计优化方案。
1 工程背景
某铝合金桁架人行天桥全长36.66 m,计算跨径35.0 m,包括主桥、梯道以及雨棚、栏杆等附属设施,主梁采用节点偏心连接的简支桁架结构,两片主桁中心轴线的间距为3.872 m,人行道板宽度为3.752 m。天桥立面如图1 所示,主梁桁架设计为12 个等距节间,节间距2.8 m,主桁架计算高度2.8 m,弧形雨棚支撑立柱高度2.06 m,上弦杆形心到上横杆形心之间高度为1.132 m,斜腹杆长度为3.38 m;桁架左端与梯道连接处设计2 个短节间,节间距1.4 m。梯道平台处桁架上弦杆断开,其余弦杆连接及其与腹杆连接均采用栓接,斜腹杆轴线与弦杆和竖腹杆不交于一点。支座位于竖腹杆底部,左端墩顶设固定铰支座,右端墩顶设滑动铰支座。主桁架上弦杆开口处在道板下侧均设有加固弦杆。

图1 铝合金人行天桥立面图(mm)Fig.1 Elevation of aluminum alloy pedestrian bridge(mm)
桥梁主体结构采用6082-T6 高强铝合金材料,材料名义屈服强度f0.2为260 MPa,弹性模量E=70 000 MPa,泊松比为0.3,材料密度为2 700 kg/m3[12]。铝合金主桁架上下弦杆截面为双槽形,端部加固弦杆截面为单槽形,竖腹杆、斜腹杆、端部上横杆和上下横梁均采用箱形截面,桥面板采用单箱三室空心板截面。主要构件截面参数见表1。

表1 天桥构件截面参数Table 1 Section parameters of components of the pedestrian bridge
2 结构受力分析
对于无节点偏心的桁架结构,可将其简化为理想结构,采用刚性节点或铰接节点模拟节点连接均可,计算结果差异很小。但是当存在较大节点偏心时,理想结构与实际结构之间差异较大,为分析节点偏心影响作用,以下分别建立理想铰接模型和考虑节点偏心模型进行对比分析。
2.1 有限元模型
不考虑桥梁下部结构,天桥上、下弦杆和腹杆均采用梁单元模拟,将梯道作用简化为桥梁结构上的集中力,边界条件按铰支座模拟。分别建立理想铰接模型和考虑节点偏心模型,理想铰接模型忽略节点偏心,而节点偏心模型中考虑到各杆件的实际连接情况,将全桥各杆件的相对位置按实际偏心值设置,使计算模型与构件实际连接情况相符。铝合金桁架连接节点具有半刚性特征,其节点刚度大小对结构受力有很大影响[13]。现有研究结果表明,铝合金盘式节点的抗弯刚度为理想刚性模型节点抗弯刚度的60%~67%[14],根据该桁架节点的实际受力状态,节点抗弯刚度较小,释放梁端约束时保留My和Mz方向30%的有效抗弯刚度。采用Midas Civil 建立桁架桥的理想铰接模型和考虑节点偏心模型如图2和图3所示,天桥结构尺寸和构件编号如图4所示。

图2 天桥理想铰接模型Fig.2 Ideal articulated model of pedestrian bridge

图3 天桥考虑节点偏心模型Fig.3 Model of pedestrian bridge considering joint eccentricity
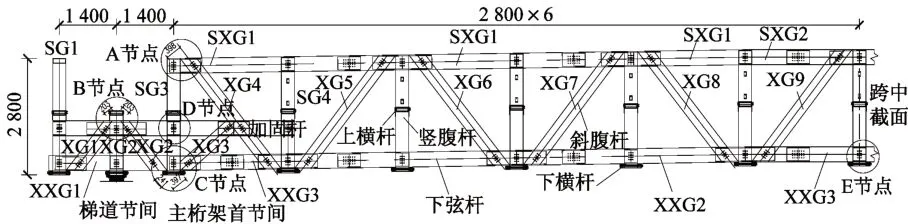
图4 1/2天桥结构尺寸和构件编号(单位:mm)Fig.4 Structure size and component number of half-bridge(Unit:mm)
根据《城市人行天桥与人行地道技术规范》(CJJ 69—95)[15]确定天桥设计人群荷载为4.131 kPa,单侧盆景和雨棚线荷载按100 kg/m取值。忽略桥面板受力作用,将其自重及人群荷载按荷载等效分配到横向连接系的上横杆上;将盆景、雨棚、梯道作用荷载作为二期荷载等效为集中荷载分配到上横杆两端及下横杆连接节点处。天桥设计基准期为50 年,根据天桥所在地风荷载按横向0.442 kPa 取值,天桥所在地为南方无雪荷载,同时对于简支梁计算中忽略温度作用。所在地抗震设防烈度为6 度,按构造措施设防。作用在天桥栏杆扶手(上弦杆)上的水平和竖向荷载不参与荷载组合。
荷载组合按基本组合确定,1.2自重+1.2二期恒载+1.4人群活载+1.4×0.7风荷载。
2.2 结果分析与探讨
《城市人行天桥与人行地道技术规范》规定,人行桁架桥上部结构在人群荷载作用下的最大竖向挠度不应超过L/800,即43.75 mm,其中L为计算跨径。在理想铰接模型中,由人群荷载计算的跨中最大竖向挠度为42.9 mm,满足规范要求;而在节点偏心模型中,由人群荷载计算的跨中最大竖向挠度为50.8 mm,不满足规范要求。根据有限元模型整理荷载基本组合作用下的计算结果见表2。
表2 中荷载组合作用下构件内力和应力结果如下:

表2 理想铰接模型与节点偏心模型计算结果对比Table 2 Comparison of calculation results between ideal articulated model and model considering joint eccentricity
(1)承载能力极限组合作用下,节点偏心模型跨中最大竖向挠度达到116.5 mm,比理想铰接模型增加15.9%;通过轴力对比发现,两结构模型构件轴力值变化不大,节点偏心模型中斜腹杆最大轴力比理想铰接模型降低7.1%。
(2)两模型构件的最大弯矩值差异较大,桁架构件SXG1左节点最大负弯矩达到-92.7 kN·m,比理想铰接模型增大337.3%,同节点构件XG4 的实际弯矩较理想情况下增加854.6%,这是由于斜腹杆(XG4)与上弦杆连接时存在很大的节点偏心距,在轴力作用下产生较大的次弯矩并发生内力重分配;在节点偏心模型中,D 节点所连接的加固弦杆和竖腹杆弯矩值较大,均超过100 kN·m。
(3)在理想铰接模型中最大拉应力61.8 MPa位于跨中下弦杆(XXG3)处,而节点偏心模型中由于次弯矩的存在,最大拉应力91.8 MPa,位于构件XG4与SXG1连接处;两模型构件压应力最大值均出现在梯道平台下方加固弦杆右端与构件SG3连接位置,分别为-118.1 MPa和-140.0 MPa;节点偏心模型中构件SG3的最大压应力也达到-138.0 MPa。虽然从数值上看,两模型构件最大应力均小于铝合金材料屈服强度260 MPa,满足规范中天桥结构强度要求,但是单槽形加固弦杆与竖杆(SG3)连接处局部应力过大,易发生失稳。
2.3 构件连接偏心次应力
理想铰接模型与节点偏心模型中截面的弯拉组合应力云图如图5、图6所示。两模型中梯道平台下加固弦杆右端与竖腹杆连接处截面应力值很大且较接近,该位置处桁架构件连接均不存在节点偏心,受次弯矩的影响较小。而有较大偏心距的节点上构件的弯拉应力存在很大差异。

图5 理想铰接模型弯拉组合应力Fig.5 Combined bending and tension stress of ideal articulated model
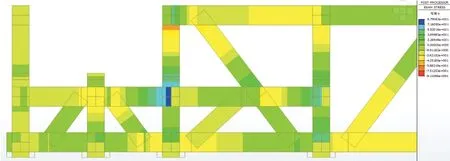
图6 节点偏心模型弯拉组合应力Fig.6 Combined bending and tension stress of eccentric model
为了对比研究次弯矩对节点连接构件应力的影响作用,选取受节点偏心次弯矩影响较大的A、B、C(如图4 所示,均位于梯道连接附近)三个节点,根据式(1)和式(2)采用线刚度分配理论计算节点处各连接构件的弯曲次应力。

式中:i为节点连接构件的编号;Mi、σi分别为节点连接构件i分配到的次弯矩和弯曲次应力;N、e分别为计算节点处偏心连接构件的轴力和节点偏心距;Ki为节点连接构件i的线刚度,Ki=EI/li,其中li为构件两端连接节点间的距离;Wzi为节点连接构件i在截面Y轴方向上的抗弯截面模量。
理想铰接模型中节点连接构件的弯拉应力和节点线刚度理论计算的节点连接构件弯曲次应力叠加得到组合应力,与节点偏心模型中相应构件的弯拉组合应力进行对比,计算结果见表3。

表3 节点偏心连接构件次应力Table 3 Secondary stress of eccentrically connecting members
由表3的计算结果可以看出:
(1)节点偏心产生的弯曲次应力效果显著。A、C节点各连接构件的弯曲次应力是轴向应力的1~3 倍,其中A 节点连接构件的弯曲次应力最大,这是由于斜腹杆XG4 具有较大的轴力和连接偏心距。竖腹杆SG3在A 节点连接处的弯曲应力超过90 MPa,过大的组合压应力影响构件稳定性和节点连接螺栓的安全性。B 节点上斜腹杆XG1和左侧加固杆的轴向应力较小,因此弯曲次应力与轴向应力的比值较大。其它节点连接构件的弯曲次应力与轴向应力比值大致相当或有所降低。
(2)A、B、C 节点各连接构件的理论计算叠加应力值与节点偏心模型计算结果基本一致,其中A 节点连接构件计算偏差在±2%以内;B、C 节点连接构件的弯曲应力计算结果偏差略大,但基本处于±13%之内。由此,模型计算与理论计算结果吻合很好,考虑节点偏心模型可以充分反映出由节点偏心连接引起的相邻构件弯曲应力的增加以及偏心次弯矩对天桥整体受力性能的影响;
(3)B、C 两节点连接构件的节点偏心模型计算值与理论计算结果偏差略大于A 节点连接构件。主要原因在于:①B、C 节点均位于梯道平台下方,该位置连接构件较多,节点间杆件相互作用,受到同一节点处两个轴力方向相反的斜腹杆所产生的偏心次弯矩重分配的影响较大;②理论计算时提取的理想铰接模型中斜腹杆的轴力略大于节点偏心结构的轴力。
3 节点连接
3.1 桁架节点连接
该桁架人行桥各构件在节点处采用A2-70 级普通不锈钢螺栓连接,螺栓抗剪强度设计值265 MPa;连接构件采用牌号为6082-T6 的铝合金,承压强度设计值215 MPa[12]。各杆件连接处均设计16 个直径为12 mm 的普通不锈钢螺栓,上、下弦杆接头通过24 个螺栓连接。A、D 两节点大样如图7 所示,16 个螺栓沿中轴线按四排间距33 mm对称布置,节点处弦杆侧面设宽度312 mm、厚20 mm铝合金连接缀板。

图7 A、D连接节点大样(mm)Fig.7 Detail drawing of A and D connection joints(mm)
3.2 节点连接强度验算及设计优化
根据《铝合金结构设计规范》[16](GB 50429—2007),在普通螺栓受剪连接中,每个普通螺栓承载力设计值应取受剪和承压承载力设计值的较小值。
受剪承载力设计值:

承压承载力设计值:

式中:nv为连接螺栓受剪面数目;d为螺栓杆直径(mm);Σt为在不同受力方向中一个受力方向承压构件总厚度的较小值分别为螺栓的抗剪和承压强度设计值。
我国《铝合金结构设计规范》中没有明确规定不锈钢螺栓的承压强度设计值,在铝合金构件连接节点设计时,由于铝合金连接件孔壁承压强度远小于不锈钢螺栓的承压强度,因此通常由不锈钢螺栓抗剪强度和连接构件孔壁承压强度控制节点设计。先将节点处构件的连接方式分解为弦杆与竖腹杆相连、弦杆与斜腹杆相连,即上、下弦杆(或加强弦杆)与腹杆通过长螺栓贯穿连接,再根据式(3)、式(4)分别计算各类型构件连接螺栓的抗剪承载力和孔壁承压承载力。桁架桥节点连接螺栓及孔壁承载能力计算结果见表4,其中螺栓连接抗力分项系数取1.3,节点承载力取螺栓抗剪承载力标准值和孔壁承压承载力标准值的较小值。

表4 桁架桥节点连接螺栓及孔壁承载能力计算Table 4 Calculation of bearing capacity of connection bolt and hole wall of truss bridge
由前文可知,存在偏心距的构件在轴力作用下会在节点连接处产生较大的次弯矩继而分配给相邻各构件,因此连接处螺栓同时受到轴心力F和扭矩T的共同作用。其中在轴心力作用下,连接工作进入弹塑性阶段后,内力发生重分布,螺栓群中各螺栓受力逐渐接近,可认为F均匀作用到每个螺栓上;而在扭矩T作用下,假定板件为刚体,螺栓为弹性体,各螺栓绕螺栓群形心旋转,产生的剪力与形心距离成正比,因此T作用下螺栓群最外侧角点处四个螺栓所受剪力是最大的。综合考虑螺栓受到的轴心力F的方向和扭矩T作用下的剪力合力方向,受剪力最大的螺栓为螺栓群最外侧角点处四个螺栓之一。
由扭矩的平衡条件得:

解得:

将扭矩产生的剪力合力NjT分解为水平分力NjTx和垂直分力NjTy:

受力最大螺栓所承受的合力Nj:

式中:n、j分别为螺栓群中螺栓的总个数和编号;rj、xj、yj分别为第j个螺栓中心距螺栓群形心的直线、水平和垂直距离;NjFx、NjFy分别为第j个螺栓受到的水平和垂直拉力分力。
提取节点偏心模型中节点各连接构件所受轴力F和扭矩T,根据式(5)-式(9)计算节点螺栓群中受力最大螺栓所承受的合力Nj,与表4 节点承载力计算结果进行对比,判断螺栓抗剪和孔壁承压是否满足规范设计要求。
根据计算结果,全桥共有4 处节点连接设计不符合要求,分别是受偏心次弯矩作用最大的2个A节点和受弯矩、轴向压应力作用最大的2个D节点(如图4,D 为加固弦杆与SG3连接节点)。同时,A、D 分别为有无节点大偏心的典型节点,E 节点为跨中处轴力最大的连接节点。桁架桥受力最不利的A、D、E 节点螺栓及连接构件承载能力验算结果如表5 所示(忽略E 节点连接处极小扭矩的影响)。

表5 关键节点螺栓及连接构件承载能力验算及设计优化Table 5 Calculation and design optimization of bearing capacity of bolts and connecting members of key joints
由表5 验算结果可知,大偏心节点A 和无偏心节点D连接构件受力最大螺栓的抗剪验算均不满足安全性要求;在孔壁承压验算中,除A节点上弦杆满足承载力要求外,其连接竖腹杆和D 节点连接构件均不满足要求;受轴力作用最不利的跨中E节点连接螺栓的抗剪验算及其连接构件的孔壁承压验算均满足承载力要求。
对E节点铝合金连接缀板的承载能力进行验算,在下弦杆拉力NFx的作用下,连接板应力σ:

其中,A为连接板沿轴力垂直方向的最小净截面面积,B=312 mm为连接板宽度,nE=4为截面螺栓孔个数,d0=13 mm 为螺栓孔直径,t=20 mm 为连接板厚度。求得E 节点连接板应力σ=113.69 MPa<215 MPa,满足规范设计要求。
针对承载能力不足的A、D 节点,从减小节点偏心量和增大节点承载力两个方面提出设计优化措施:
(1)A 为大偏心节点,减小A 节点偏心量至150 mm 可使节点受力最大螺栓的合力减小至75 kN,从而满足节点连接验算要求。但A 节点偏心次弯矩的减小无法大幅度降低D 节点的扭矩,且D 无节点偏心,因此只能对螺栓和连接构件进行加强。
(2)将节点连接螺栓直径由M12 加大为M16,为满足孔位最小间距要求,螺栓之间的横向间距由33 mm 增大为40 mm,经验算仍无法满足D节点承载能力要求。
因此,将D 节点连接的梯道平台下方加固弦杆与竖腹杆SG3 连接由单槽形梁改为双槽形梁,增加螺栓受剪面个数和构件孔壁承压面积以增大节点承载力。由表5 验算结果可知,优化后的节点螺栓抗剪承载力和连接构件孔壁承压承载力均满足承载能力极限状态下的节点连接设计要求。
4 结论
(1)通过铝合金桁架桥理想铰接模型和考虑节点偏心模型对比分析,发现杆件节点偏心使结构最大变形量增加约16%,而节点偏心产生的次弯矩大幅度增加了构件的应力,最大增加101.8%,构件最大组合压应力达到140 MPa。
(2)按节点线刚度分配原理计算的构件弯拉组合应力与考虑节点偏心模型结果吻合较好,偏差在13%以内。节点偏心产生的弯曲次应力与轴向应力比值基本在1~3 之间,部分杆件弯曲次应力远大于轴向应力,节点偏心对构件的弯曲次应力影响较大,设计时应充分考虑节点偏心影响作用。
(3)按照规范进行螺栓及连接构件承载能力验算,结果显示,在节点连接大偏心情况下有4 处节点螺栓抗剪验算不符合设计要求,部分受力最不利的节点孔壁承压验算不满足规范要求。减小大偏心连接节点的节点偏心量至150 mm 可使其节点受力满足设计要求,对于仍未满足受力要求的节点须采取加大连接螺栓直径、改变加固弦杆截面形式等提升节点承载力的优化措施。
