像移补偿装置运动学建模及解耦分析

卢明明， 金钰博， 杨雪梅， 刘长青

(长春工业大学 机电工程学院， 吉林 长春 130012)

0 引 言

像移补偿装置是一种检测机载相机成像质量的设备，具有像移误差补偿功能。装置由台体和三个轴框架组成，可以近似看成三轴转台，是一个要求非常高的非线性系统[1]。目前，随着三轴平台技术的不断发展成熟，不仅在国防和军事领域占据首要地位，而且在人们日常生活中的作用也越来越突出，逐渐成为一个国家国防、经济实力与军事实力的重要标志[2-3]。同时，它也为一些机载设备的有效性验证提供可靠的实验平台。随着航天、航空工业的发展，像移补偿装置的应用范围越来越广。

像移补偿装置作为检测机载相机成像质量的设备，具有像移误差补偿功能的优劣性直接关系到仿真和测试实验的可靠性与置信度，是保证航空航天产品精度及性能的基础[4]。

航空、航天相机拍摄时，由于载机的运动、相机的摆动、温度等因素影响，曝光时目标物体与感光介质间存在相对运动，致使成像模糊和拖尾效应，即像移[5]。虽然将相机搭载于飞机上通过多次飞行测试相机的成像性能是最直接的方法，但由于完成一次飞行任务需要消耗巨大的人力、财力、时间和资源。为减少飞行次数、提高试验效率、节省资源，进行实验室内动态模拟成像试验就显得尤为重要[6-7]。

像移补偿装置通过对其三个轴架施以不同的运动来模拟飞机各种飞行动作和姿态，即横滚运动、俯仰运动和偏航运动[8]。装置运动时各个框架间存在惯量以及动力学耦合，直接影响控制的动、静态指标以及系统的稳定性[9-10]。当装置各轴架同时工作时，各轴架不仅受到自身框架产生的力矩，还会受到其他框架的干扰力矩，框架间存在非线性动力学耦合，会影响到控制系统精度和动态性能，严重时会导致整个控制系统的失控，因此需要进行解耦设计[11]。文中在分析像移补偿装置框架间耦合问题的基础上，给出各轴架的运动学方程，利用李导数算子理论验证了其可解耦性，并对其进行解耦；最后运用Matlab对转台系统进行系统仿真，证明了解耦的有效性。

1 像移补偿装置机械结构分析

像移补偿装置由台体和三个轴架组成，三个轴架为横滚轴架、偏航轴架与俯仰轴架。三个轴架的机械系统主要由俯仰、航向、横滚轴系结构组成。其中，横滚轴的结构是U形，俯仰轴与航向轴的结构是O形。光学系统安装在航向轴系内，并能随航向轴绕航向轴偏航；扫描镜结构与俯仰轴系统一起绕俯仰轴旋转；两部分作为一个整体安装在外框内，并与横滚轴系统一起转动。整体结构如图1所示。

图1 像移补偿装置整体结构

像移补偿装置三维视图如图2所示。

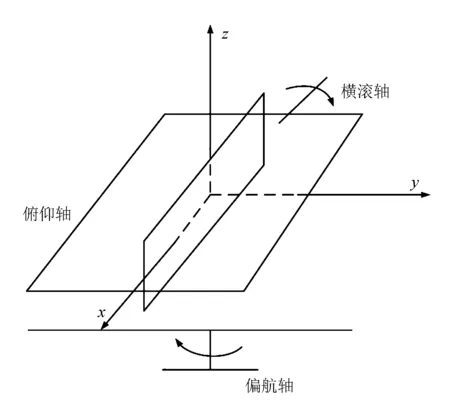
图2 像移补偿装置三维视图

由图2可知，像移补偿装置的三个轴在运动过程中并不相互独立，而是相互影响。因此，利用装置运动学建模,并对其进行解耦具有非常重要的意义。

2 三轴架运动学建模

设定x,y,z为俯仰轴架所固连的坐标系，x′,y′,z′为偏航轴架所固连的坐标系，x″,y″,z″为横滚轴架所固连的坐标系，φ、α、φ分别为三个轴电机转角，M1表示偏航轴对俯仰轴作用力矩，M2表示横滚轴对偏航轴作用力矩，M3表示偏航轴对横滚轴作用力矩，其中M1,M2,M3在XYZ,X′Y′Z′,X″Y″Z″坐标系分别投影。

设定i,j,k和i′,j′,k′分别为俯仰轴XYZ和偏航轴X′Y′Z′坐标轴上的单位向量，当俯仰轴相较偏航轴转动一个角度φ时，对自变量x做三角变换，sin(X)=sX,cos(X)=cs，根据i′,j′在XYZ内的投影，可求出i′,j′与i,j的关系为：

i′=icφ-jsφ,

j′=isφ+jcφ,

k′=k。

(1)

当偏航轴相对于横滚轴转过一个角度α时，i″,j″,k″为横滚轴X″Y″Z″三个坐标轴上的单位向量，根据投影求出i″,j″与i′,j′的关系为：

i′=icα-k″cα,

k′=i″sα+k″cα,

j′=j″。

(2)

设定T为偏航轴的转动惯量矩阵，T′为俯仰轴的转动惯量矩阵，T″为横滚轴的转动惯量矩阵，其中T,T′,T″分别位于XYZ,X′Y′Z′,X″Y″Z″坐标系内，G1,G2,G3分别代表三个轴架所受的重力，G,G′,G″均位于X″Y″Z″坐标系内，俯仰轴的重心在XYZ坐标系内表示为(x1,y1,z1)，偏航轴的重心在X′Y′Z′坐标系内表示为(x2,y2,z2)，可得到以下矩阵：

2.1 俯仰轴架运动学建模

表示。

设

ω1=ωX1i1+ωY1j1+ωz1k1。

对ω1进行求导可得，

其中i,j,k向XYZ内投影后皆为零向量，所以有

根据刚体定点运动方程

推导出动力学模型，将式(1)、式(2)联立代入可得

(3)

由于G1=G1K″，由式(1)、式(2)可有

G1=G1(-i′sα+k′cα)=

G1[-(icφ-jsφ)sα+kcα]=

-cφsαG1i+sφsαG1j+cαG1k。

所以将G1向XYZ投影可有

G1=-cφsαG1i+sφsαG1j+cαG1k=

(4)

根据式(3)可以得到

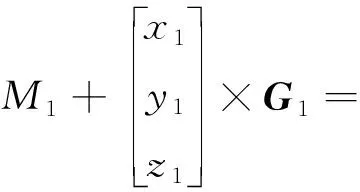
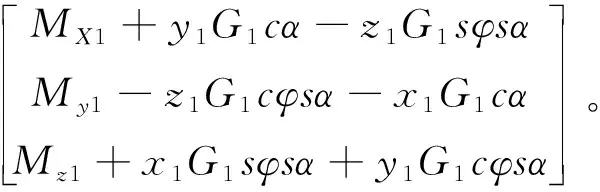
(5)

将式(5)代入式(3)后整理,可得俯仰轴运动微分方程

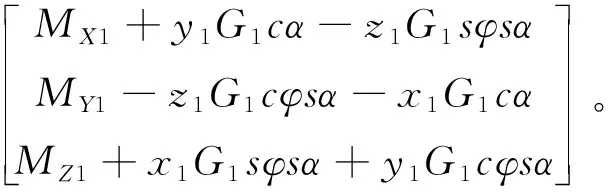
(6)

2.2 偏航轴架运动学建模

设

ω2=ωX2i′+ωY2+ωZ2k′。

对ω2求导可有

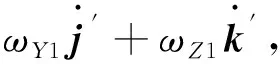
(7)

其中

由俯仰轴的刚体定点运动微分方程可知

将相应的参数代入后可得

(8)

又由G2=G2k″，所以由式(2)可有

G2=G2(-i′sα+k′cα)，

所以将G2向X′Y′Z′投影有

(9)

M1=MX1i+MY1j+MZ1k=

MX1(i′cφ+j′sφ)+MY1(-i′sφ+j′sφ)+MZ1k′=

(MX1cφ-MY1sφ)i′+(MX1sφ+MY1cφ)j′+MZ1k′=

将上式继续整理：

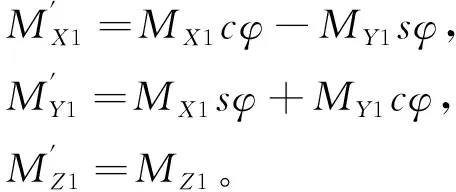
(10)

联合式(9)、式(10)可得

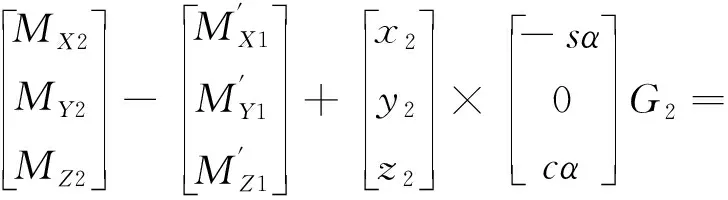
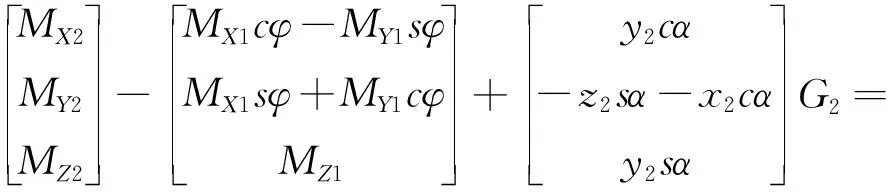
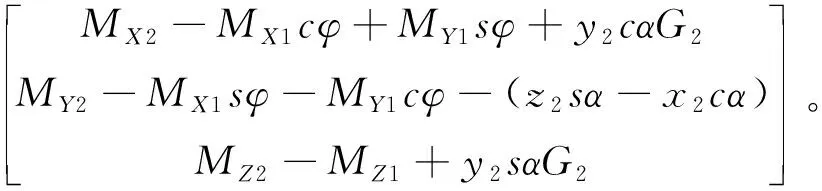
(11)

将式(11)代入式(8)可得偏航轴运动学微分方程

2.3 横滚轴架运动学建模

设

ω3=ωX3i″+ωY3j″+ω23k″,

对ω3进行求导,有

由俯仰轴的刚体运动微分方程可得

代入后可得

(12)

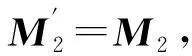
M2=MX2i′+MY2j′+MZ2k′=

MX2(i″cα-k″sα)+

MY2j″+MZ2(i″sα+k″cα)=

(MX2cα+MZ2sα)i″+

j″+(-MX2sα+MZ2cα)k″=

所以有

(13)

可以得出

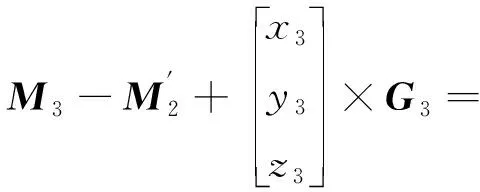
(14)

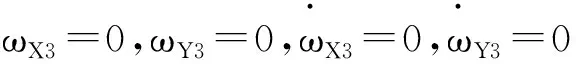
(15)

3 三轴架运动学耦合仿真分析

由上可知，像移补偿装置受驱动力矩作用，为验证像移补偿装置存在耦合性，采取观察一轴运动时对其余两轴耦合情况进行分析的方法，即令一轴运动，通过仿真方法得到其余两轴角度和角速度耦合曲线。

1)令偏航轴运动，观察俯仰轴与横滚轴运动时的耦合情况。

给定偏航电压为40 V，俯仰轴与横滚轴电压为0 V，频率为10 Hz，偏航、俯仰、横滚轴架的初始位置分别为：φ=90°,α=0°,φ=0°，受到耦合驱动力矩作用下的角位置与角速度的变化曲线如图3所示。

(a) 滚转角度

(b) 滚转角速度

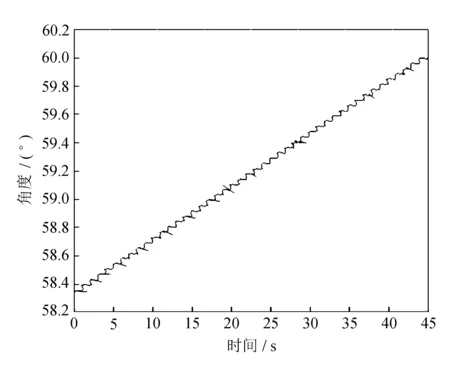
(c) 俯仰角度

(d) 俯仰角速度图3 偏航轴驱动力矩作用下俯仰轴与横滚轴变化曲线

由图3可知，横滚轴的耦合角度比较显著，已经超过0.6°；俯仰轴的耦合角度也达到了1.5°。

2)令俯仰轴运动，观察偏航轴与横滚轴运动时的耦合情况。

给定俯仰轴电压为24 V，偏航轴与横滚轴的电压为0 V，频率为10 Hz，俯仰、偏航、横滚轴架的初始位置分别为：φ=90°,α=0°,φ=0°，受到俯仰轴驱动力矩作用下偏航轴与横滚轴变化曲线如图4所示。

(a) 横滚角度

(b) 横滚角速度

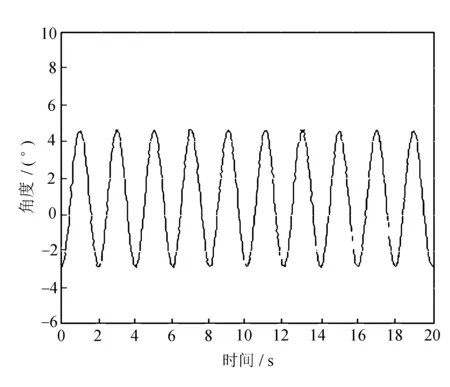
(c) 偏航角度

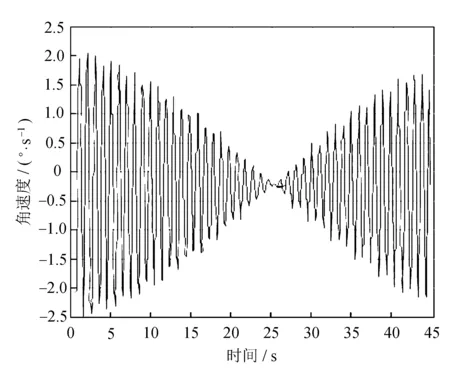
(d) 偏航角速度图4 俯仰轴驱动力矩作用下偏航轴与横滚轴变化曲线

由图4可知，耦合引起的横滚轴滚转角速度误差可达10%，而且偏航轴角度与角速度的耦合都比较明显。

3)令横滚轴运动，观察偏航轴与俯仰轴运动时的耦合情况。

给定横滚轴电压为30 V，偏航轴与俯仰轴的电压为0 V，频率为10 Hz；俯仰、横滚、偏航轴架的初始位置分别为：φ=0°,α=0°,φ=90°，受横滚轴驱动力矩作用下偏航轴与俯仰轴变化曲线如图5所示。

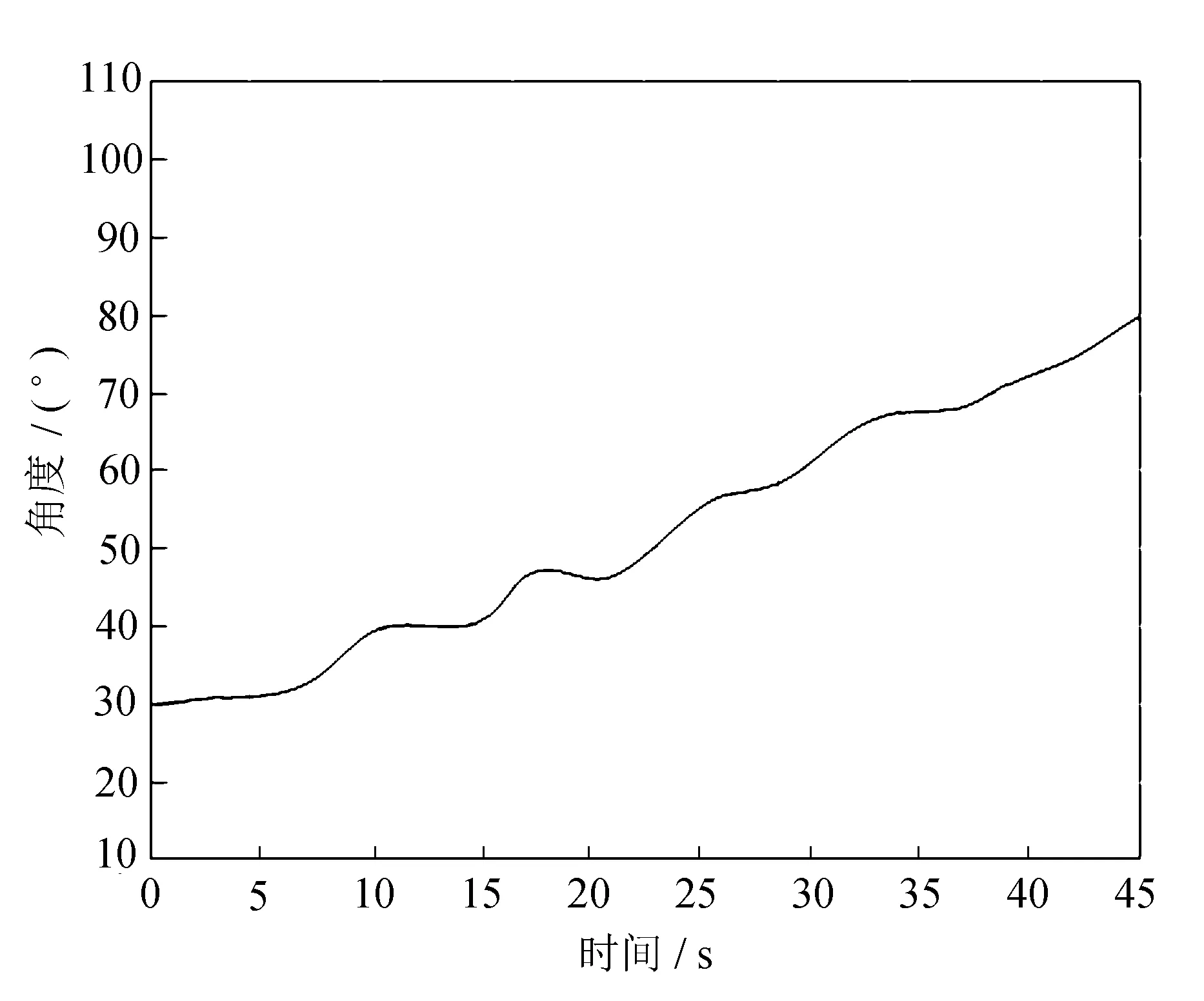
(a) 偏航角度

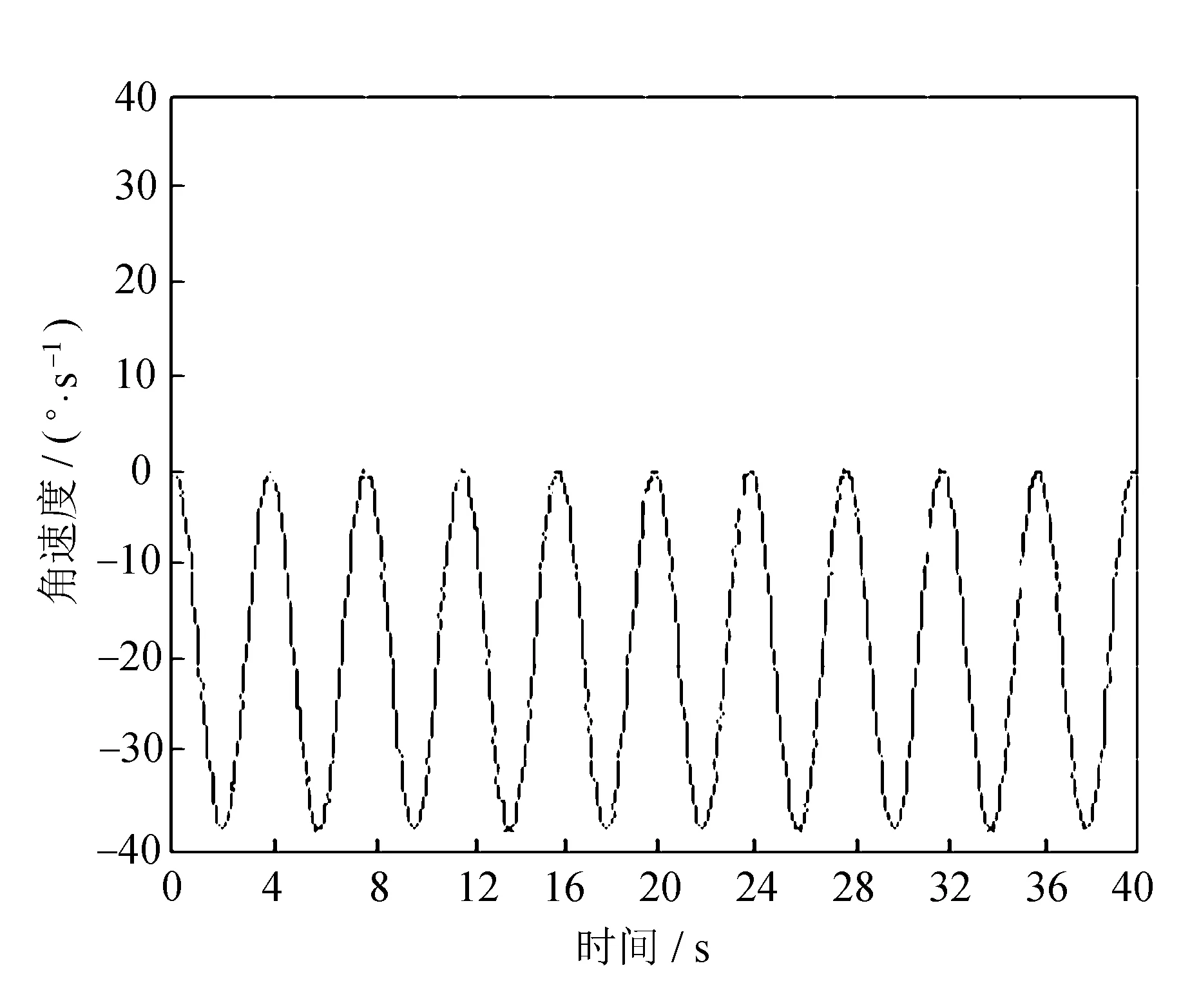
(b) 偏航角速度

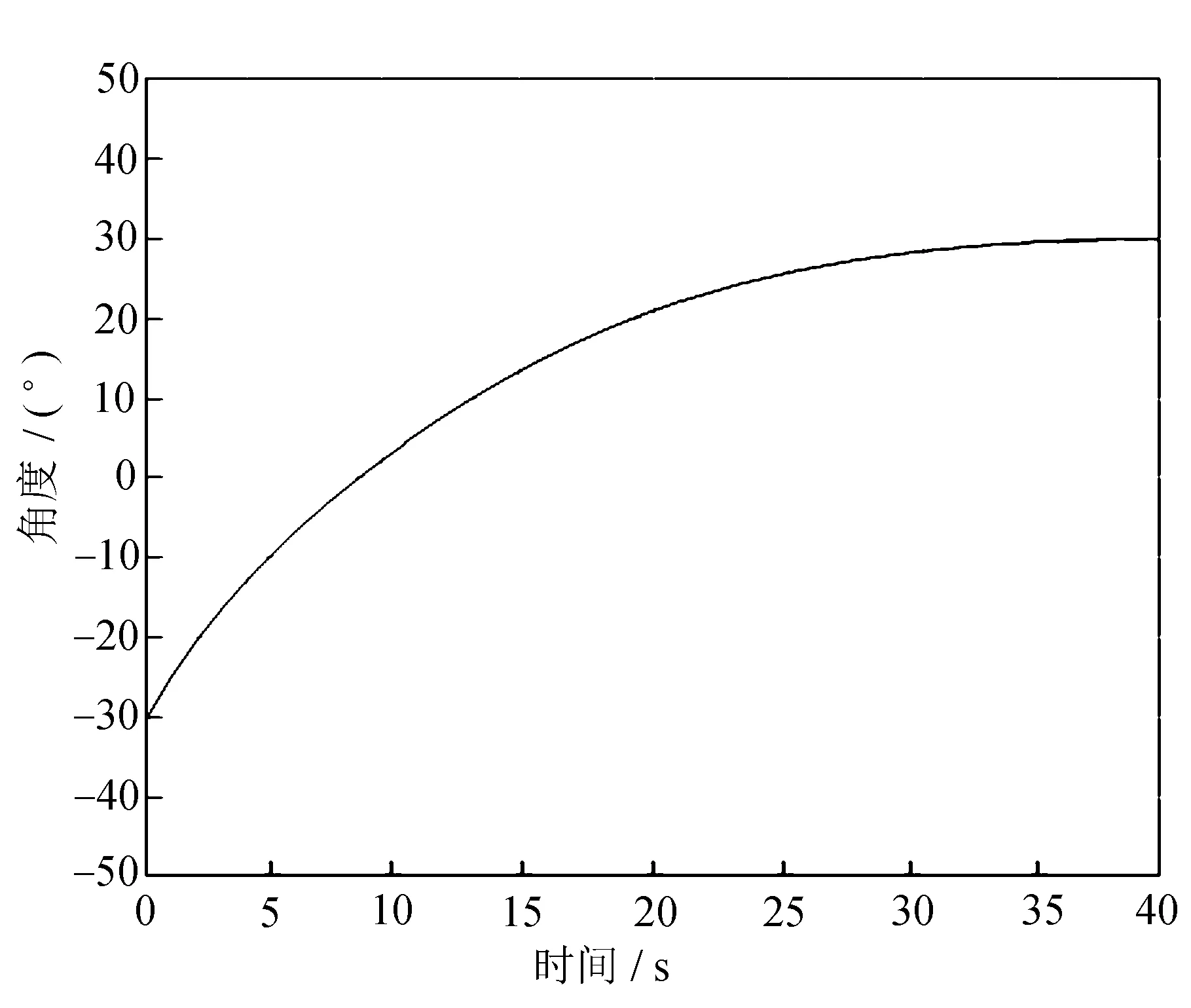
(c) 俯仰角度

(d) 俯仰角速度图5 横滚轴驱动力矩作用下偏航轴与俯仰轴变化曲线

由图5可知，偏航角度误差可达50°，俯仰已达到60°，而且偏航角速度整体偏向负方向，俯仰角速度明显加快，耦合明显。

从图3～图5可以看出，给任意一轴施加驱动力矩时，另外两个轴都受耦合影响，以上可以证明像移补偿装置各轴系之间存在严重耦合现象。所以要想实现像移补偿装置的精密控制，就要找到抑制外界干扰对像移补偿装置系统性能影响的办法，因此需要对像移补偿装置进行解耦。

4 解耦仿真分析

基于李导数解耦后得出如下三个SISO系统，即俯仰轴、偏航轴、横滚轴。

同样在像移补偿装置受到驱动力矩的情况下，三个轴架在施加驱动力矩作用下仿真得到的系统耦合关系分别如图6～图8所示。

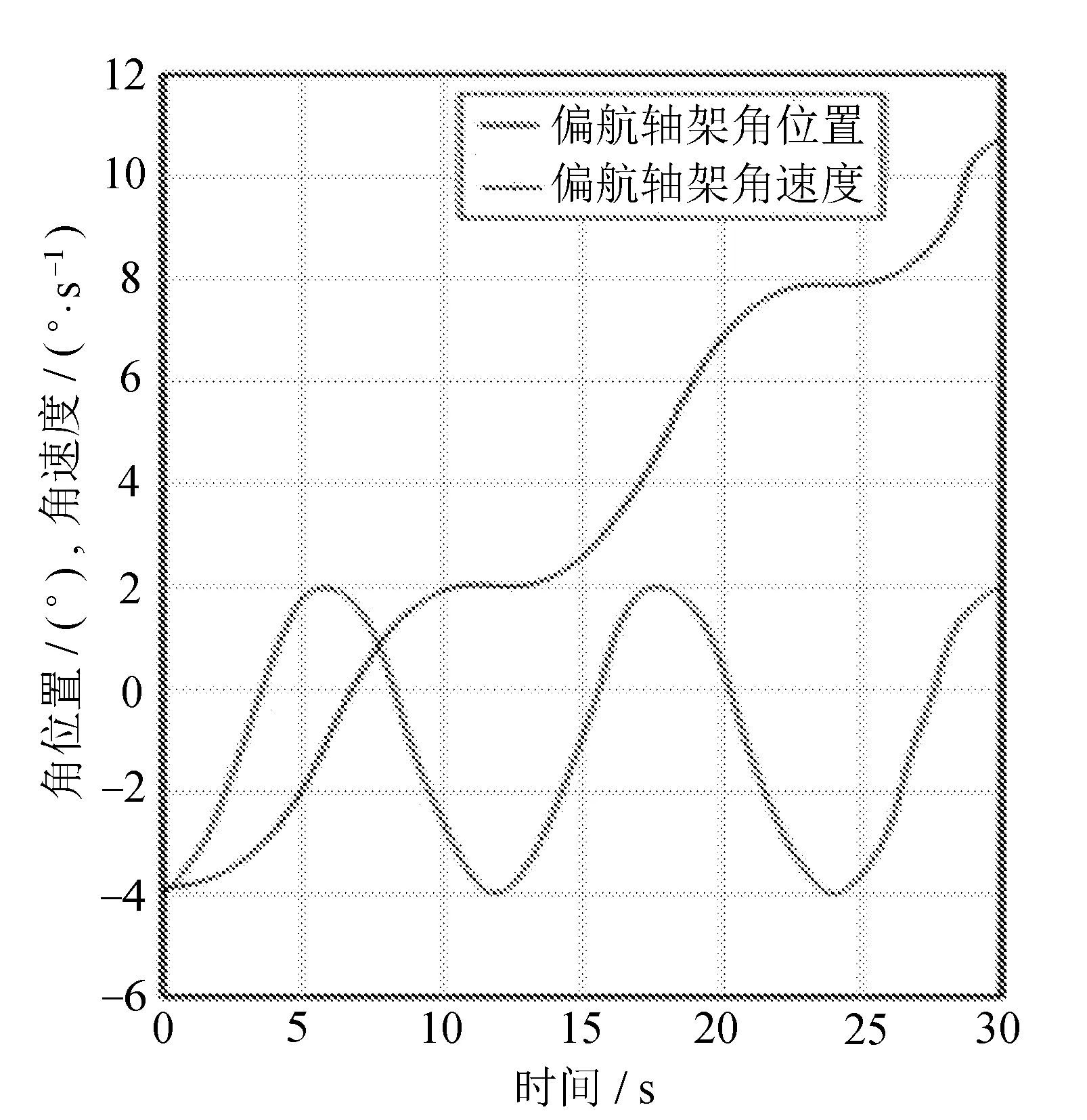
(a) 俯仰

(b) 横滚图6 偏航轴驱动力矩下的俯仰耦合与横滚耦合曲线

图6仿真结果显示，单独给偏航轴施加驱动力矩时，对于解耦后的等效系统而言，横滚轴和俯仰轴的角位置与角速度几乎为零，由此可知，横滚轴和俯仰轴并未受到偏航轴的耦合影响。

(b) 俯仰图7 俯仰轴驱动力矩下的偏航耦合和俯仰耦合曲线

从图7可以看出，对于解耦后的系统而言，单独给俯仰角施加驱动力矩指令时，偏航轴的角度与角速度在0处波动，横滚轴的角度与角速度也同样在0处波动，由此可知，俯仰轴并未对偏航与横滚轴带来影响，即耦合消失。

(b) 俯仰图8 横滚轴驱动力矩下偏航耦合与俯仰耦合曲线

从图8可以看出，单独给横滚轴施加驱动力矩指令时，对解耦后的系统来说，俯仰的角度与角速度在0处波动，偏航的角度与角速度也同样在0处波动，由此可知，横滚轴并未对偏航与横滚轴产生影响，即耦合消失。

5 结 语

针对像移补偿装置运动时存在耦合情况，对装置进行耦合分析，提出了李导数解耦，并对解耦后的系统进行仿真分析。

根据李导数算子完成了解耦控制器的设计，最后对解耦后的系统进行仿真，在对系统进行解耦后结果表明，无论单独给哪个轴施加驱动力矩，另外两个轴几乎没有变化。由此表明，解耦之后各轴之间干扰消失，解耦状况良好，实现了三个轴之间的相互独立运动，不再相互影响。