基于离散元的高陡堆石边坡失稳过程模拟
2022-01-07郑成成龙小刚胡广柱马春辉李高超
郑成成,龙小刚,胡广柱,袁 祥,马春辉,李高超
(1.陕西镇安抽水蓄能有限公司,陕西 西安 710061;2.西安理工大学水利水电学院,陕西 西安 710048;3.省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048)
西部大开发战略推动了我国西部地区的水利、交通、市政等基础设施建设的快速发展。由于西部地区多高山峡谷地貌,在工程建设中易形成高陡边坡工程,如由弃渣料堆积形成的高陡堆石边坡。这些高陡边坡在自重、水压力、作业荷载、风化和侵蚀等外部因素的影响下,其发生失稳的可能性将极大增加。边坡失稳对工程运行、建筑物和人员安全都将会产生严重影响,高陡边坡的稳定性已经成为影响和制约工程建设与运营的关键问题之一[1]。因此模拟高陡边坡失稳过程,明确其影响范围是工程领域中重要的研究课题。
边坡稳定问题一直是工程建设中的重要研究内容,众多学者采用各种稳定分析方法求解边坡稳定相关问题,例如极限平衡法、有限元法、离散元法等。在传统极限平衡法方面,陈祖煜等[2]将二维Spencer法扩展到三维条件下,提出了边坡稳定分析的三维极限平衡法,并通过工程实例证明了其可行性。卢坤林等[3]将条柱间作用力等效为滑面正应力,提出了适用于空间形态滑面的边坡三维极限平衡法。冯树仁等[4]提出了能够考虑多种滑面类型的边坡三维极限平衡方法,并提供了计算程序和验证算例。Jiang等[5]在极限平衡分析方法的框架下考虑了土体性质的二维空间变异性,提出了定量的边坡破坏风险评估方法。此外,有限元法在边坡稳定分析中也取得了良好的应用效果。史卜涛等[6]将坡顶竖直位移突变作为边坡失稳判据,为边坡稳定性分析提供了新思路。林姗等[7]提出了虚单元强度折减法,较真实地模拟滑裂面形态的多样性,用于土石混合体边坡的稳定性分析。蒋水华等[8]提出基于非侵入式随机有限元法的边坡可靠度分析方法,是解决复杂边坡可靠度问题的有效手段。由于极限平衡法和有限元法分析方法具有连续介质特征,对非黏土、岩石混合体等离散介质的边坡分析效果并不十分理想,Lu等[9]通过对比滑动稳定分析方法,认为离散元法更适合研究岩、土体破坏特性。Weng等[10]采用离散元法研究了边坡角度、裂隙角度和材料劣化等影响下板岩边坡的变形行为。毛佳等[11]根据滑坡问题的普遍性与重要性,探讨了三维滑坡体的运动路径、堆积范围,提出了三维距离势函数离散单元法。周健等[12]运用离散元方法分析土坡稳定性,并分析了其破坏机理。蒋明镜等[13]提出了胶结尺寸离散元微观接触模型,研究了不同节理边坡的破坏形式,并模拟了边坡失稳演化过程。Xu[14]运用离散元方法模拟三轴试验,研究了颗粒细观参数对黏性土宏观特性的影响。李世海等[15]通过对比滑坡稳定分析方法,认为将计算模型与现场监测结果相结合,是判断边坡稳定的最有效方法。Lu等[16]认为离散元方法能够较好地模拟强降雨条件下径流路径、颗粒速度和滑动影响范围,为滑动灾害预警和决策支持提供有效信息。汪儒鸿等[17]结合边坡灾前位移变形程度、坡体解体现象等,采用颗粒离散元方法分析堆积体边坡的突变失稳问题。赵兰浩等[18]提出了适用于非均匀离散颗粒体系的接触检测算法,具有内存占用较小等优点,对于大规模、分布密集、大粒径比的颗粒体系具有较高的计算效率。Wang等[19]建立了基于位移统计的离散元分析方法,并将其与抗剪强度折减法相结合,分析高陡顺层岩质边坡的稳定性。黄达等[20]为进一步探明软硬互层反倾边坡的倾倒变形机制,融合离心模型试验与离散元模拟,研究了此类边坡的破坏模式与影响因素。
通过上述分析可知,学者们采用极限平衡法、有限元法、离散元法等方法研究了水利、岩土工程中的岩质、土质边坡稳定性问题,但对于特殊土体的边坡稳定性及其失稳过程研究较少。为此,本文利用离散元方法对高陡堆石边坡进行数值模拟,重点研究极限工况下的边坡失稳过程,详细分析其堆石运动、挡墙受力以及边坡整体变化情况,旨在为高陡堆石边坡稳定分析、失稳过程和影响范围研究提供思路和方法。
1 离散元原理及模拟方法
离散元数值模拟方法不仅可用于砂石等非连续介质的细观力学行为研究,还可用于求解实际工程中非连续变形问题[21]。离散元的基本思想是将非连续介质分成有限个单元的集合,并使每个刚性单元体满足接触本构关系。随后,根据牛顿第二定律,建立离散元方法的运动方程并进行积分求解,得到单元体的速度、位移等物理量,经过多次循环计算后求得非连续介质的运动状态。离散元的主要优势体现在对非连续介质问题的处理上,允许单元间存在相对运动,可以将单个微观介质的运动状态进行宏观放大,具有原理简单、计算速度快等优势。因此,离散元方法适用于模拟块体属性明显的物体的静、动力特性,如高堆石边坡失稳过程模拟,其在重现堆石边坡或块石的位移、速度等方面具有很好的效果。离散元原理如图1所示。

图1 工程弃渣区域与办公区域平面布置
在建立堆石边坡离散元模型过程中,所采用的主要模拟技术与方法如下:①不同粒径块石生成:根据粒径级配曲线,采用挤压排斥法生成堆石料离散元三轴试验模型与堆石边坡离散元模型。②不平衡力计算:当边坡无明显位移,颗粒平均不平衡力小于0.1N,且最大不平衡力与平均不平衡力之比小于10时,可认为离散元模型已处于最终的稳定状态。③能量计算:通过在每个时间步对模型中的墙体、球体进行能量分析,并将势能、动能和摩擦耗能等进行分类合计,由此可得整个离散元模型的能量变化。④挡墙上作用力计算:通过监测球体作用在挡墙上的合力变化,实现对挡墙作用力的监测。
2 工程背景与离散元模型建立
某日调节抽水蓄能电站工程规模为Ⅰ等大(1)型工程,多年平均发电量23.41亿kW·h。电站上水库正常蓄水位1 392.00 m,死水位1 367.00 m,有效库容856.00万m3;下水库正常蓄水位945.00 m,死水位910.00 m,有效库容956.10万m3。为修建上下库连接路,在道路沿线的自然沟谷或地形低洼处修建了4个施工平台,其中1号施工平台与工程弃渣场的平面布置如图1所示。建成后的1号施工平台为大型堆石边坡,最高处高程为1 116.40 m,最低高程为916.60 m,最大高差199.80 m。
在堆石边坡初始建设阶段,由于未能及时有效地平整弃渣料,导致降雨后弃渣体排水不畅,出现了局部泥石流现象。该次滑动最远滑至边坡下游与主沟道汇合处,存在影响工程弃渣场排洪洞泄洪安全的隐患,现场情况及汇合处位置关系如图2所示。小规模泥石流发生后,在堆石边坡的中部、底部分别修建了石笼挡墙和混凝土挡墙,以增强堆石边坡的整体稳定性。因此,考虑到工程后期运行管理营地位于弃渣场主沟道的下游,堆石边坡的可靠运行将直接影响运行人员生命安全及抽水蓄能工程的安全运行。

图2 早期泥石流现场情况
采用传统极限平衡法计算堆石边坡稳定性,其安全系数略大于1,安全储备较小。为进一步分析高陡堆石边坡的稳定性,综合考虑堆石边坡所在区域的地形特征、边坡体型特征和堆渣特点等,确定了最不利的边坡二维剖面并建立了离散元模型,其现状局部如图3(a)所示,二维剖面如图3(b)所示。相较于三维模型,二维模型忽略了实际地形对坡体、滚石等缓冲作用,将缓冲作用作为堆石边坡的安全富裕,因此二维堆石边坡稳定分析针对的是边坡安全稳定的最不利情况。本文使用商业软件进行离散元建模与计算,其水平与竖直方向的尺寸分别为945 m×312 m,共包含10 528个块石颗粒,其底部基础、石笼挡墙、混凝土挡墙均由wall构建[22]。关于堆石边坡离散元中的块石模拟,本文对堆石边坡材料级配曲线进行适当地截取与放大,使模型在计算精度与计算效率间得到了较好的平衡,并通过模拟施工工况发生的小规模滑动,验证了离散元模型的可靠性。

图3 1号施工平台(单位:m)
依据堆石料室内大三轴试验结果、堆积边坡级配曲线,建立了堆石边坡离散元三轴试验模型,对堆石料的细观线性刚度模型参数进行标定。现场取样获得的堆石料级配曲线如图4(a)所示,据此建立的堆石料离散元三轴试验模型如图4(b)所示。采用基于本构模型的堆石料细观参数标定方法进行计算[20],确定颗粒的法向接触刚度kn=3.5 MN/m,切向接触刚度ks=2.6 MN/m以及摩擦因数μ=0.09,其标定结果如图5所示。此外,在离散元计算中设定基岩面与块石的摩擦因数均设定为0.30,考虑到系统中存在的其他阻尼,将局部阻尼设定为较小值0.10。通过查阅资料以及参考相关的工程经验,确定石笼挡墙和混凝土的摩擦因数分别为0.35和0.20。
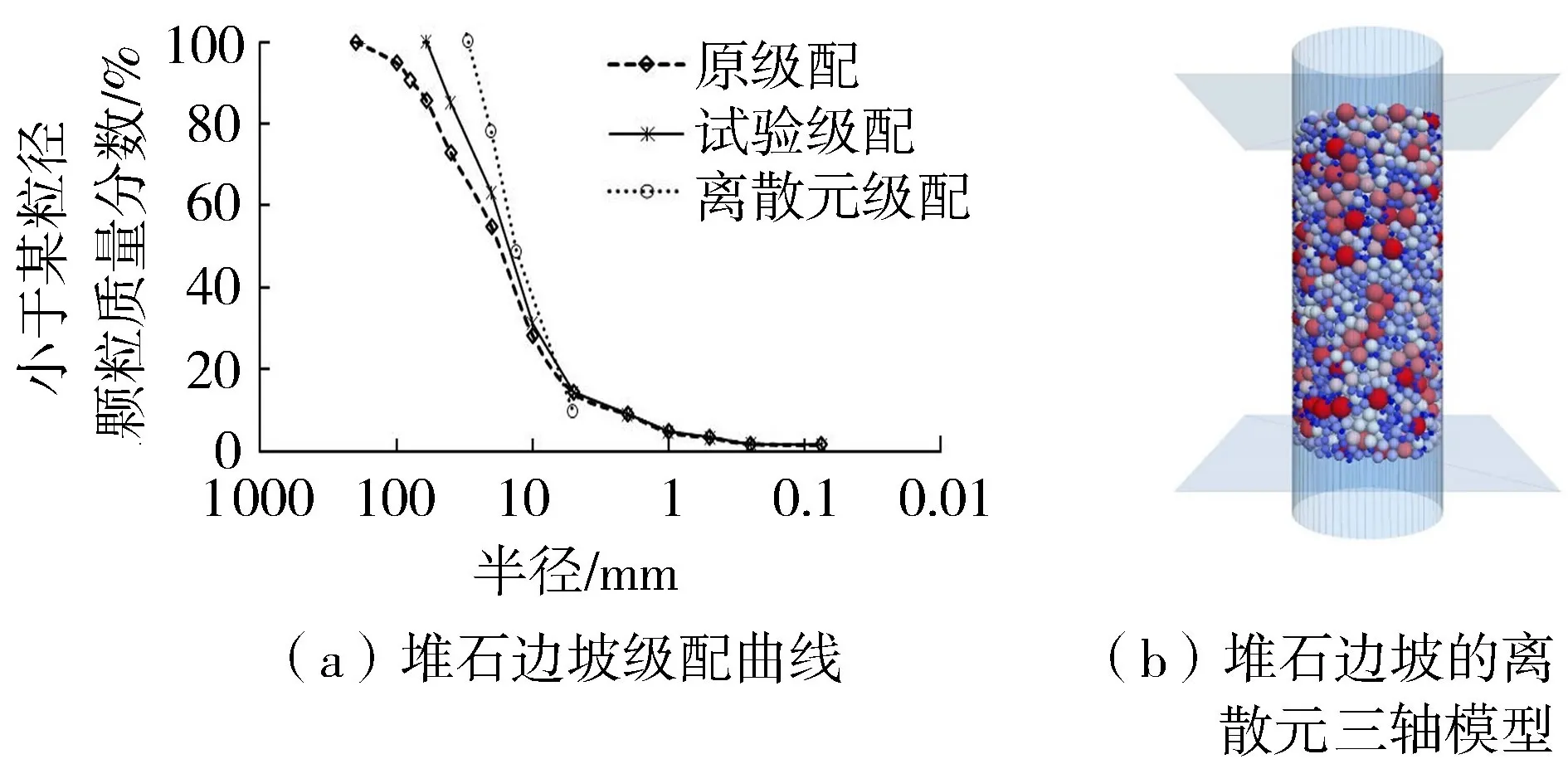
图4 堆石边坡离散元三轴试验模型

图5 堆石边坡的室内三轴试验与离散元模拟结果
3 堆石边坡失稳过程模拟
在建立上述离散元模型的基础上,模拟运行工况下堆石边坡的失稳过程,整个失稳过程共持续418.38 s,其平均不平衡力比的变化过程如图6所示,其体型变化如图7所示。由图可知:0~32.32 s为滑动启动与快速滑动阶段,通过对比图7(a)与图7(b)可知,在该阶段堆石边坡顶部、中部处于不稳定状态的块石迅速发生滑动。堆石边坡顶部1 070 m高程以上的块石滑向下游,直接导致石笼挡墙以上边坡的块石层厚度明显增加。堆石边坡中部的水平向300~400 m区间内块石滑向下游,混凝土挡墙虽对块石运动起到了一定的阻挡作用,但是仍有大量颗粒越过混凝土挡墙滑向下游;32.32~139.52 s堆石边坡进入局部滑动阶段,对比图7(b)与图7(c)可知,该阶段堆石边坡上部块石越过石笼挡墙,堆积到堆石边坡中下部的后缘部位;139.52~189.21 s堆石边坡滑动缓慢,仅有个别块石越过石笼挡墙滑向下游;随着堆石边坡中下部前端块石的下滑,在后缘块石的推动作用下,堆石边坡中下部再次发生滑动。通过对比图7(d)与图7(e)可知,堆石边坡中下部和后部变化较为明显,且部分块石已滚落至河床部位;在235.99~418.37 s时段内仅有个别块石运动,滚落至河床的块石数量有所增加,直至边坡整体达到稳定状态。

图6 堆石边坡失稳的平均不平衡力比过程线监测
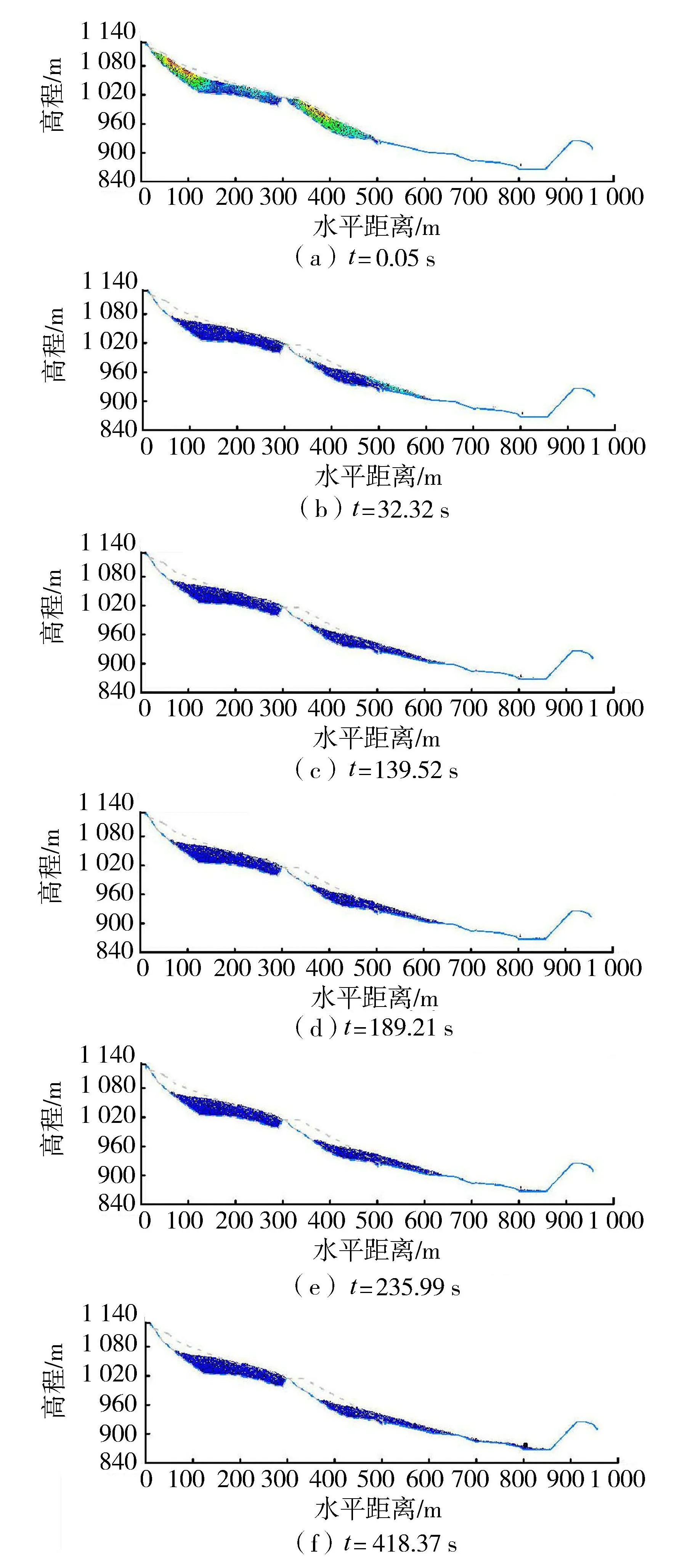
图7 运行工况下堆石边坡各阶段体型
在堆石边坡失稳过程中,块石平均水平向速度、平均竖直向速度和平均速度变化情况如图8所示,水平向速度以顺坡向为正,竖直向速度以向下为正。由图8可知,块石的速度变化情况与堆石边坡失稳过程中各阶段的划分基本一致:①在边坡失稳的初始阶段,块石平均速度急剧增大,随后逐步减小,其平均速度最大值出现于3.73 s,为4.34 m/s。过程中,块石的平均水平向速度明显大于平均竖直向速度,这表明该阶段块石主要以水平向顺坡运动为主;②在后续各阶段中,块石速度的变化规律与各阶段的运动态势基本相符,多以块石的水平向运动为主,竖直向运动为辅。

图8 堆石边坡堆石速度变化
堆石边坡初始状态与失稳后状态的块石分布情况如图9所示,水平方向上块石分布范围由初始状态的0~480 m失稳后扩展至40~840 m。在堆石边坡上部,峰值的块石数量由383个增加至403个,表明石笼挡墙起到了明显的阻滑作用,堆石边坡上部的块石堆积现象更加明显。在堆石边坡中下部,其水平方向的颗粒分布曲线明显后移,表明中下部块石滑向下游,块石在水平向上的分布更加分散。对于块石的竖直向分布,其变化规律、原因和水平向分布基本相同。此外,块石所在位置的最大高程值下降,表明最高处的块石出现下滑,同时堆石边坡中下部块石分布曲线出现下移,表明该处块石出现明显下滑。相比于石笼挡墙,受混凝土挡墙阻挡的堆石边坡中下部块石分布曲线改变更为明显,表明堆石边坡底部的混凝土挡墙更需要加强。

图9 堆石边坡运行工况模型
堆石边坡失稳发生后,块石的水平向、竖直向位移统计如图10所示,由图可知:对于水平向位移,运动距离为40 m的块石数量最多,运动距离超过200 m后块石数量明显减小;对于竖直向位移,运动距离为10 m左右的块石数量最多,块石的最大下降高度为148.5 m。

图10 运行工况边坡失稳后堆石边坡块石位移统计
通过监测越过石笼挡墙、混凝土挡墙的块石数量,能够明确边坡失稳过程以及挡墙所发挥的阻滑作用,其变化情况如图11所示,由图可知:对于石笼挡墙,其以上部位的块石在滑动初期不断越过石笼挡墙滑向下游,直至123 s后无块石越过石笼挡墙。上述分析表明:石笼挡墙的修建有效地阻挡了堆石边坡上部块石向下游滚落,对维持其上部块石的稳定起到了明显的阻滑作用。对于混凝土挡墙,滑动启动后,边坡中下部的块石不断越过挡墙,直至264 s后无明显增加。对于到达河床底部的块石数量,其在213 s后几乎不再发生变化,到达河床底部的块石多数来源于边坡中下部的堆石,因此加强边坡底部工程措施将有助于减少块石滚落至河床的可能性。因此,石笼挡墙、混凝土挡墙的修建起到了增加堆石边坡稳定性及减少块石滑落的重要作用。

图11 堆石边坡越过特定位置块石数量变化监测
堆石边坡滑动结束后,越过石笼挡墙、越过混凝土挡墙和到达河床的块石粒径情况如图12所示。由图可知:越过石笼挡墙、越过混凝土挡墙的块石粒径均为均匀,与堆石边坡整体的粒径基本一致。对于距离更远的河床位置,粒径大小表现出明显的递增趋势,表明粒径大的块石更容易滚落至更远的位置。

图12 运行工况下越过特征位置的堆石边坡粒径统计
通过监测挡墙上所受压力的变化,能够掌握堆石边坡块石滑动下挡墙承受的冲击力情况,以及挡墙所受到的最大压力,从而为挡墙的设计提供依据。在堆石边坡失稳过程中,石笼挡墙与混凝土挡墙的单宽受力变化如图13所示。由图可知,滑动启动后,在大量块石的冲击下挡墙受力迅速增加,随着滑动的发展挡墙受力处于波动状态,当滑动逐渐停止时挡墙受力逐渐趋于稳定。对于石笼挡墙,其初始受力为1.98 MN/m,在块石的冲击下挡墙受力在57.83 s时达到峰值9.51 MN/m,因此挡墙在动力情况下的受力为静力情况的4.8倍。对于混凝土挡墙,其初始受力为1.10 MN/m,在块石的冲击下挡墙受力在10.93 s时达到峰值4.15 MN/m,因此挡墙在动力情况下的受力为静力情况的3.8倍。相比于石笼挡墙,混凝土挡墙在边坡失稳过程中的受力变化不断发生变化,表明堆石边坡的中下部处于不断调整中,其对混凝土挡墙受力亦有着持续的影响。
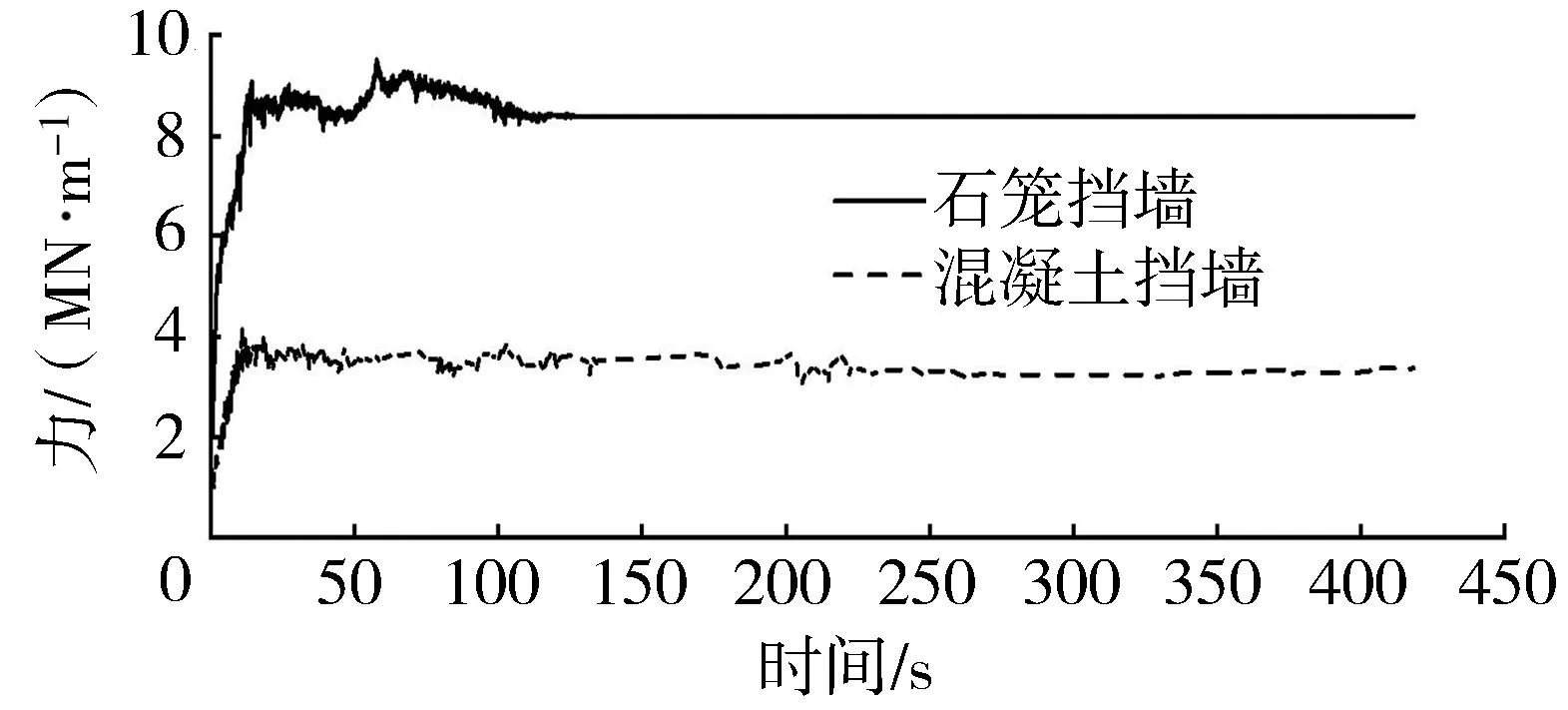
图13 堆石边坡挡墙上游面受力变化监测
在堆石边坡失稳的过程中,堆石边坡的能量变化如图14所示。滑动体的动能变化反映了在滑动过程中滑动体所携带的能量及其对防护工程造成破坏的能力。在t=3.51 s时滑动体动能出现峰值,与上述分析中块石平均速度达到最大值的时刻相同,此时滑动体动能可达3.05×108J。峰值时刻坡体将携带巨大能量冲击石笼挡墙与混凝土挡墙,对其安全稳定造成一定的影响。重力做功在滑动体启动初期增长较快,后期增长速度变慢,表明堆石边坡逐步趋于稳定。接触累积耗能也随时间逐步增长并趋于稳定,表明滑动体在运动过程中内部不断发生碰撞、摩擦,消耗了大量能量。阻尼累积耗能主要为局部阻尼耗能。

图14 堆石边坡失稳过程中的能量变化
4 结 语
针对高陡堆石边坡,采用离散元法对边坡失稳过程进行定量分析。主要结论如下:①高堆石边坡的失稳过程总体可分为启动与快速滑动阶段、局部滑动阶段、平稳阶段、再次局部滑动阶段、最终平稳阶段;②在整个边坡失稳过程中,块石平均速度初始阶段较大后缓慢减小,主要以水平向顺坡为主,竖直向运动为辅;③通过比较初始阶段和最终状态块石分布、块石越过特定位置的数量、粒径统计和挡墙上游面的受力情况表明:采用石笼挡墙等工程措施能够明显起到了阻滑的作用,但混凝土挡墙迫切需要加强;④在堆石体边坡失稳过程中,滑坡体将携带的大量动能,对防护措施造成的一定冲击。通过离散元数值模拟,揭示了高陡堆石体边坡整个失稳过程,并验证了施工措施的阻滑效果,为特殊材料工程的失稳过程模拟、工程措施设计提供了模拟思路和方法。
