激光三角法微位移测量的算法比较

徐瑞超 胡艳凯 线 晨

陕西国防工业职业技术学院 机械工程学院 西安 710300

1 研究背景

在工程测量中,激光测距占据着极其重要的位置。激光测距的方法有很多,主要有激光三角法[1]、激光脉冲法[2]、激光相位法[3]、调频连续波激光雷达法[4]等。激光三角法以结构简单、体积小、易于实现、精度高、速度快的特点,得到广泛应用。激光三角法可以用于零件的尺寸测量,在三维轮廓及产品质量检测中也经常用到,可以大幅提高检测精度和检测效率。激光三角法还在交通、医学、农业、机器视觉等领域得到了应用,大大促进了各相关领域的发展[5-6]。

在工业生产中的许多领域,如无损检测、逆向工程等,需要运用非接触式测距,这样可以提高企业生产力,并且对于产品质量的提升也有益处。在许多工业应用场合中,粗糙目标的非接触式测距扮演着重要的角色。激光位移技术在工程测量领域有广泛应用,是非接触测量的一种。另外,激光位移技术在军工行业、航天航空领域等也有广泛应用。激光位移技术应用范围广,商业价值高,需求空间大。激光位移传感器的使用使测量系统具有更小的体积、更低的功耗、更高的精度,原因在于使用了激光位移技术。并且凭借安全、方便的特点,激光位移技术逐步向电子化发展。

基于上述背景,笔者对激光三角法微位移测量的算法进行比较,提出基于激光三角法的物体微位移测量方案。

在研究中,搭建试验平台,进行标定,获取数据,并使用高斯拟合法[7]、传统灰度质心法[8]、二次方加权质心法[9]进行精度比较分析。

2 测量原理

激光三角法可以依据测量方式、光线原理、入射光形态等方式进行分类。按照测量方式,分为直射式与斜射式。按照光线原理,分为反射式与透射式。按照入射光形态,分为单束光与结构光[10-11]。

直射式与斜射式测量,采用的都是反射光测量。散射性好的物体表面,更适合采用直射式测量。测量面比较光滑的物体,更适合采用斜射式测量,因为接收的光线是正反散射光。直射式测量具有光强集中、光斑小、误差小的特点。斜射式测量虽然体积大、测量范围小,但是测量分辨率高,当被测物体离镜头比较近时,使用斜射式测量更为合适。除直射式和斜射式测量外,透射式测量常用于特殊材质。结构光测量用于曲面扫描,也被称为光切法,具有测量速度快、简单的特点,但同时结构复杂,成本高。考虑到测量分辨率的要求,笔者采用斜射式测量,搭建试验平台,进行试验获取数据,利用多种算法进行数据分析,从而比较各种算法的优劣。

斜射式激光三角法原理如图1所示。成像透镜的主光轴与被测物体表面的交点为O点,对应的参考平面在线性阵列电荷耦合器件上的成像点为O1点。激光器发射出的激光经过汇聚透镜组漫反射,通过成像透镜组汇聚,这样在电荷耦合器件上对应成像点形成一个三角形,被测物体的位移y可以通过电荷耦合器件光斑移动位移x求得。

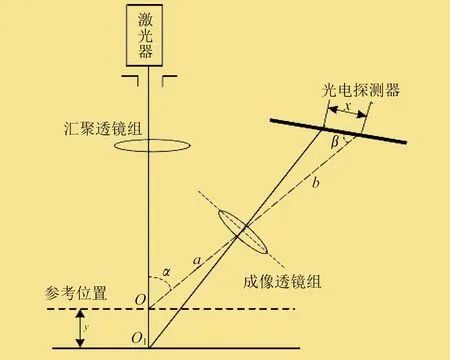
图1 斜射式激光三角法原理

整个光路由多个部分组成,分别为激光器、汇聚透镜组、孔径光阑、成像透镜组、光电探测器。光束从激光器发出后,垂直入射经汇聚透镜组聚焦至物体表面,经物体表面发生漫反射,反射光经过成像透镜组由光电探测器接收。被测物体移动时,光电探测器上接收的点也会移动,从而使物体位移量和探测器光电移动量存在一定的物理关系。成像透镜光轴与激光器轴心交于一点,以该点垂直于激光器轴心位置作为基准面,即物体的参考位置,对应关系经过推算得:

(1)

式中:α为激光器光轴所在直线与成像透镜组光轴所在直线之间的夹角;β为光电探测器所在面与成像透镜组光轴所在直线之间的夹角;a为光点在物体上的位置与透镜中心的距离;b为光电探测器表面接收的光点与透镜中心的距离。

当物体远离激光器方向移动时,式(1)中符号取负,反之取正。

搭建的试验平台如图2所示。采用光学平台作为试验台,将各个器件固定在试验台上,保证稳定性,减小振动。在激光器、透镜和电荷耦合器件的固定单元中加入可调器件,方便调焦。试验中使用的成像透镜口径为1.5 mm,汇聚透镜为平凸透镜,焦距为12.5 mm,口径为2 mm。

图2 试验平台

3 算法

图片的分辨率可以通过图像处理来提高,但不可能无限提高,仅仅依靠改进图片分辨率很难达到要求,提高系统精度需要使用其它方法。通过算法处理达到对电荷耦合器件光斑细分定位的目的,对于提高系统精度有一定作用。光斑细分定位算法有很多,如质心法、曲线拟合法等,都可以起到提高光斑定位精度的作用。笔者采用灰度质心法、二次方加权灰度质心法、高斯拟合法,对光斑定位,通过系统标定,比较分析各种算法定位精度的不同。

3.1 灰度质心法

设线性阵列电荷耦合器件上光斑大小为m个像素,视频输出信号呈高斯曲线分布,光斑形成的输出信号的灰度质心坐标X为:

(2)

式中:xi为第i个像素位置;f(xi)为第i个像素位置光斑的灰度值。

3.2 二次方加权灰度质心法

二次方加权灰度质心法灰度质心坐标X为:

(3)

3.3 高斯拟合法

通常,高斯分布较为常见,光斑在电荷耦合器件上成像的灰度信息近似呈高斯分布状态,所以灰度分布可以使用高斯曲线进行拟合。高斯拟合法计算式为:

(4)

式中:U为光斑灰度质心坐标;A为灰度幅值比例因数;e为方向标准偏差;e0为高斯函数中心;σ为曲线半宽度;u0为像素位置光斑灰度的最小值。

高斯拟合法抑制噪声能力较好,定位精度较高,但同时也存在一些缺陷,物体表面的变形会影响精度,更容易受到物体表面粗糙度的影响,使测量精度不能得到保证。传统灰度质心法受噪声影响大,对于中心像素信息提取不足,抗干扰能力较弱,精度也不能得到保证。将待处理的灰度值用实际灰度值的二次方来表示,是二次方加权质心法的处理方式,作用在于对图像中心信息信噪比的充分利用,从而得到更好的抗干扰性能。

4 试验分析

物体实际位移与标定计算位移试验数据见表1。表1中,y0为物体实际位移,xa为高斯拟合像点位置,y1为高斯拟合计算位移,xb为传统灰度质心法像点位置,y2为传统灰度质心法计算位移,xc为二次方加权灰度质心法像点位置,y3为二次方加权灰度质心法计算位移。

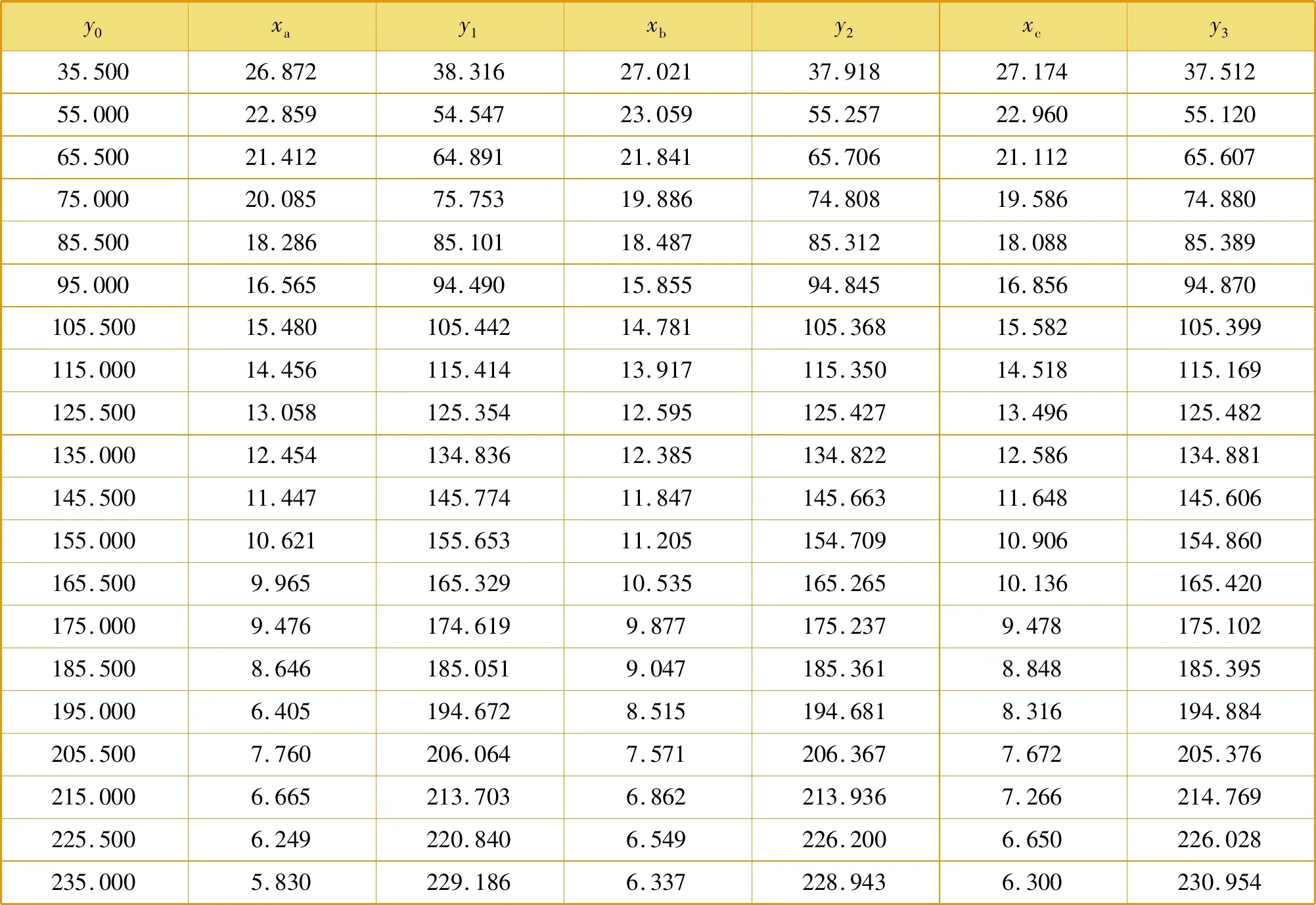
表1 物体实际位移与标定计算位移试验数据 mm

按照三种算法试验数据分别计算位移,得到最大误差、平均误差、均方根误差。三种算法试验数据误差见表2。

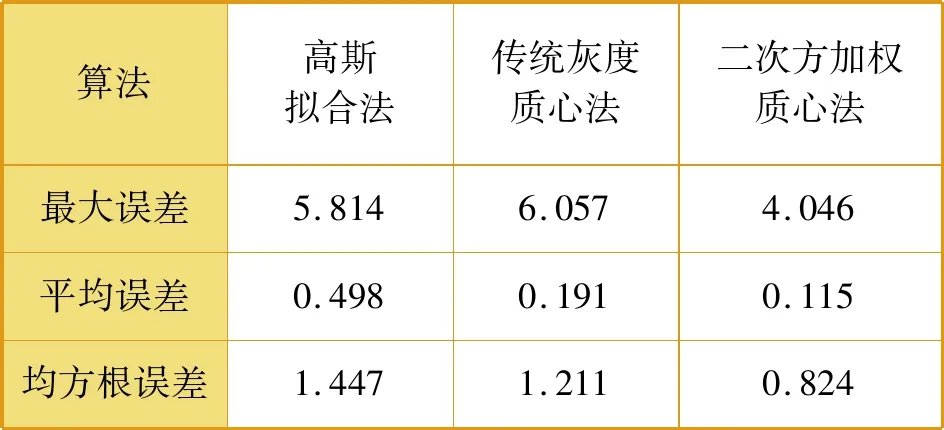
表2 三种算法试验数据误差 mm

由表2可以明显看出,在35～235 mm测量范围内,二次方加权质心法处理后的数据标定误差最小,测量的平均误差仅为0.115 mm,误差对比结果与理论分析一致。

取80～200 mm之间的位移数据,采用同样方法进行分析,得到三种算法位移数据误差,见表3。

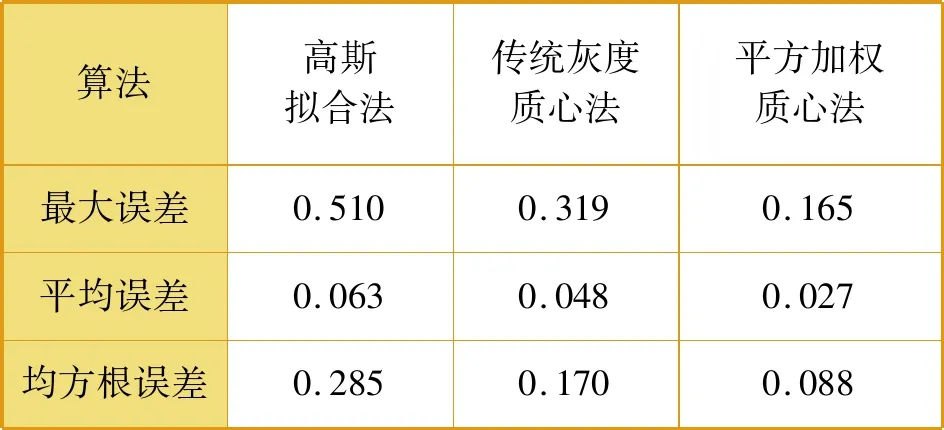
表3 80～200 mm位移数据误差 mm

由表3可知,三种算法的误差均减小,可见位移传感器两端测得的数据对整个系统的影响较大,给系统带来了较大的误差,当取中间段进行分析时,误差明显减小。其中,二次方加权灰度质心法的均方根误差仅为0.088 mm。

5 结束语

笔者对激光三角法微位移测量的算法进行比较,搭建试验平台,测量物体位移。试验结果表明,系统精度与所采用的算法相关。与传统灰度质心法和高斯拟合法相比,二次方加权质心法具有更高的精度,并且抗干扰性能较强。探索更好的光斑细分定位算法用于光斑细分处理,可以提高精度,这是未来的研究方向。