基于DE−GWO算法的矿井风网风量调节方法
2022-01-07吴新忠张芝超王凯韩正化魏连江
吴新忠,张芝超,王凯,韩正化,魏连江
(1. 中国矿业大学信息与控制工程学院,江苏徐州,221116;2. 中国矿业大学安全工程学院,江苏徐州,221116)
矿井通风可向井下各用风场所提供足够的新鲜风量,同时排出井下的污浊气体,从而满足矿井安全生产的需求[1]。在生产推进过程中,矿井的通风设施、风网结构等都会随之改变,从而使得通风系统中分支风量也在逐渐变化,当分支风量变化超过一定范围时就会引起某些分支发生粉尘积聚、瓦斯浓度超限等问题,对矿井的安全生产带来较大影响[2]。由于实际的矿井通风系统巷道众多、网络结构交错纵横,使得矿井的日常管理及风量调节变得更复杂。如果对每条分支进行风阻分析来调节系统各个分支的风量,工作量会非常大且不易实现。因此,在满足用风地点的需风量条件下,应依据各分支在通风网络中的可调性以及合理性来选择调节分支[3],使得风量调节后的各分支风量均满足安全生产要求。
近年来,国内外学者对复杂通风网络解算与风量调节技术展开了深入研究。文献[4]开发了矿井通风系统可视化管理平台,提出了智能型通风控制系统,从整体上提高了对复杂风网解算和系统优化的效率。文献[5−6]从矿井通风智能调控角度出发,构建了智能型通风控制系统,为矿井通风系统智能化奠定了基础。文献[7]提出了通风网络风量分配和风流调控一体化的优化思路,通过余树弦风量和回路矩阵来计算风网风量分配值和风阻调节值,并基于典型通风网络实例验证了该方法的有效性和可行性。
虽然矿井通风相关研究较多,但对需风量变化实时处理和智能控制的研究较少。因此,本文通过风网灵敏度求出最优的可调分支集和风阻调节范围,经差分灰狼算法(differential evolution grey wolf optimizer,DE−GWO)实现寻优,得到需风分支风量可调范围,提出根据分支风量期望值来选择不同调节分支的智能应急调风方案,并基于矿井智能控制系统实验平台进行验证,以期为矿井应急调风提供理论和实践指导。
1 风网灵敏度及其在风量调节中的作用
1.1 灵敏度理论
在通风网络中,当j分支的风阻Rj发生变化,且变化量为ΔRj时,会使风网中i分支的风量Qi发生变化,若分支i风量的变化量为ΔQi,当|ΔRj|→0时,
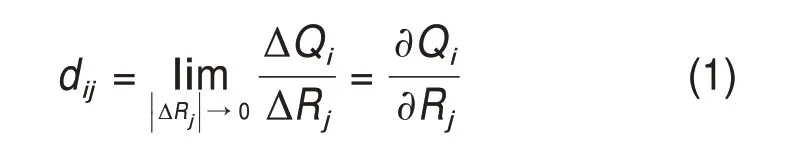
式中:dij为分支i风量相对于分支j风阻变化的灵敏度[8],灵敏度绝对值|dij|越大,表示分支j风阻的变化对分支i风量的影响程度越高。
1.2 灵敏度矩阵的求解
矿井通风网络在风量调节过程中需遵循节点风量平衡和回路风压平衡定律。节点风量平衡定律是指在通风网络中任一节点的流入风量之和等于流出风量之和,其表达式为

式中:N为网络中分支总数;M为通风网络的节点数。
回路风压平衡定律是指通风网络中任一闭合回路的各分支能量代数和为0,其表达式为:

式中:pj为j分支的风机风压、自然风压的代数和,若无该项则取0。
通过式(2)和式(3)对分支风阻Rj求偏导可得灵敏度微分方程组:

1.3 风量调节点的选择及调阻范围的确定
对于具有n条分支的通风网络,经过灵敏度微分方程组的求解,可计算出风网灵敏度矩阵D:

风网灵敏度矩阵D在某一固定状态下是唯一的。
若风网中需增加分支i的分配风量,则选择调节的分支j需满足dij> 0;反之,若要减小分支i的风量,则调节分支j需满足dij< 0。当采用增阻调节来增大分支i的风量时,需要选择灵敏度矩阵中第i行的较大值;反之,如果减少分支i的风量,那么需选择第i行的较小值[9]。当通风网络参数变化时,风网工作状态也会随之改变,灵敏度会随着分支风阻的变化而变化,灵敏度衰减率tij表示为
通过大量的风网数据拟合与模拟分析发现,灵敏度dij与风阻Rj之间存在如下关系:

式中:a和b为常数,可通过回归方程分析求得。
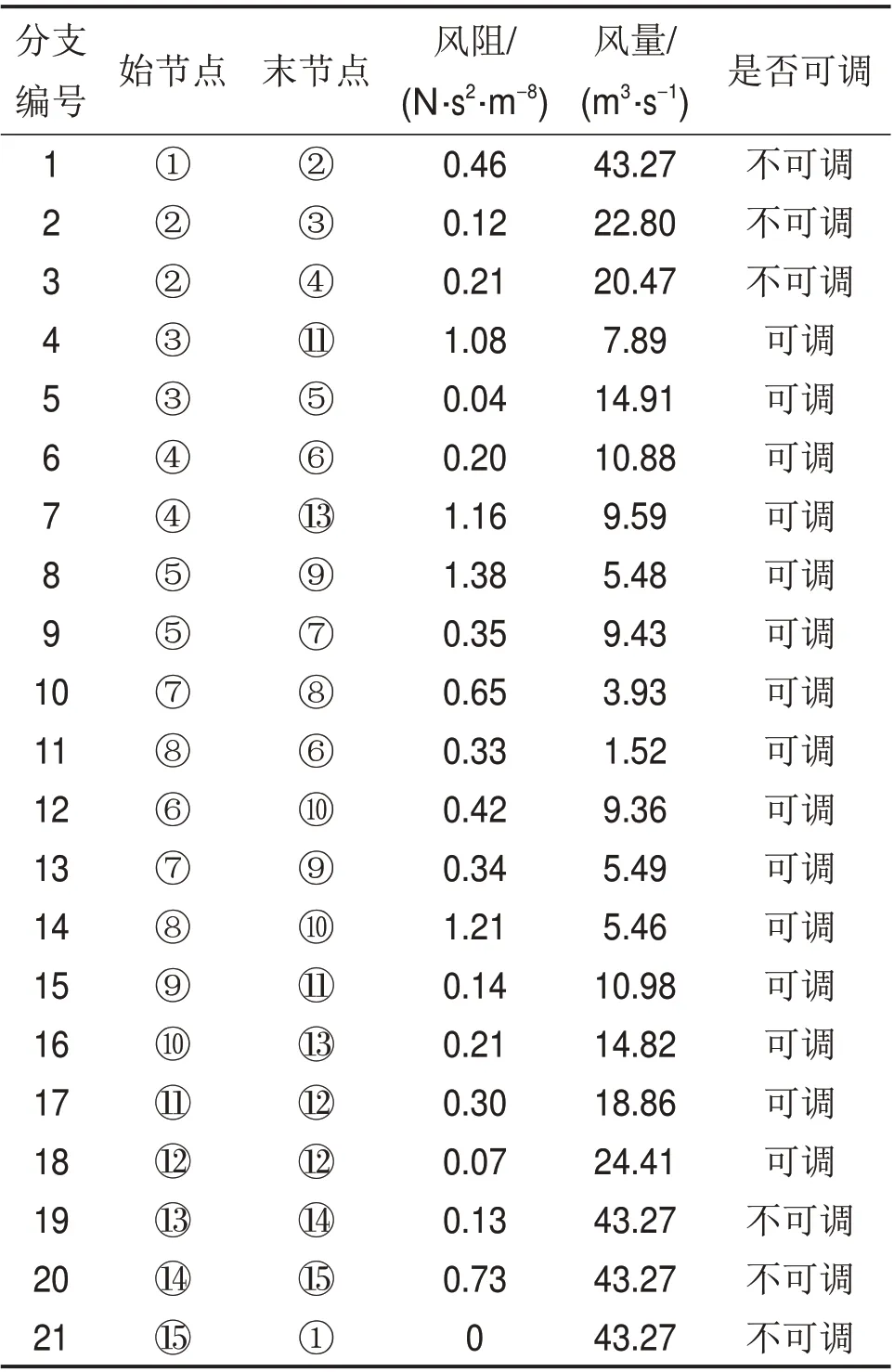
通过灵敏度衰减率可知,随着调节分支风阻Rj增大,灵敏度dij在不断减小,即风量Qi的变化幅度在减小。当风阻Rj超过临界值Rjmax时,风量Qi的变化幅度很小,即调风进入了迟钝的区域;当分支风阻Rj 在矿井通风网络中,当风路i发生瓦斯超限时,若瓦斯浓度超出正常值幅度较小,通过对单条分支调阻就可以满足需风要求;但当瓦斯浓度超出正常值幅度较大时,就需要对多条分支同时调阻来增大需风分支的风量。为了确定需风分支风量可调范围,本文以通风网络中需风分支风量可调最大化作为通风网络优化的目标函数即Fmax=Qi,其中Qi为待调需风分支的风量。 风量调节优化过程中除了遵循节点风量平衡、回路风压平衡以及满足风网分支最小需风量之外,还要从安全方面考虑。通用矿用轴流式通风机的特性曲线图中会出现类似马鞍形状的“马鞍区”,矿用通风机可以正常运行在“马鞍区”右侧的工况点处,若因通风系统中通风阻力增大或通风机风量波动导致工况点移至“马鞍区”左侧,则矿用通风机可能会发生喘振,造成损失和危害[10]。一般轴流式扇风机实际工作风压Hf不能高于最高风压Hfmax的90%,运转效率η下限为60%。 从上述条件可以看出,通风网络风量调节优化模型为非线性约束问题,通常使用罚函数将约束条件以惩罚项的形式包含到适应度函数中来简化该问题。由于差分灰狼算法对目标模型的可微性并无限制,从而避免了不可微精确罚函数[11]不能处理不可微函数的缺陷,能够有效求解目标函数可行的极值点。 加入惩罚项后的目标函数F为 式中:γ,φ,λ和μ均为惩罚参数;Rjmin和Rjmax分别为Rj可调节的最小值和最大值;Qjmin为j分支的最小需风量。 灰狼优化算法(grey wolf optimizer,GWO)是受灰狼种群的社会等级和狩猎行为启发得到的一种新型种群智能优化算法[12]。 3.1.1 社会等级制度 灰狼种群具有严格的社会阶级架构,一般划分为4 个社会等级。灰狼中社会等级最高的狼是α,处于金字塔的顶端,为狼群的领导者,其次是β和δ,负责协助α的工作,而整个寻优过程主要由最底层的狼ω来实现,ω狼负责完成高层狼交代的任务,不断地搜索猎物的位置。α,β和δ这3种高等级个体共同负责指定ω移动的方向,并根据ω不断传回的反馈信息实时更新自己的位置。 3.1.2 狩猎行为 寻优过程会通过跟踪、环绕逼近的方式寻找猎物,环绕阶段种群位置更新如下: 式中:D为灰狼个体与目标猎物之间的距离;t为当前迭代次数;Xp(t)和X(t)分别为第t次迭代后猎物的位置和搜索个体当前位置;A和C为控制参数, 式中:Tmax为最大迭代次数;参数a在迭代过程中由2递减到0;r1和r2为随机数值,0≤r1,r2≤1[13]。 3种高等级个体α,β和δ在进攻阶段时负责定位猎物的位置,并指引其他搜索个体ω完成靠近、攻击等行为,最终达到捕获猎物的目的。该过程可表示为: 式中:Dα,Dβ和Dδ分别为α,β和δ与搜索个体ω间的距离;X1,X2和X3分别为搜索个体ω经α,β和δ指引后下一步移动的位置;Xα,Xβ和Xδ分别为第t次迭代后个体α,β和δ距离猎物的位置;X为搜索个体当前位置;A1和C1为灰狼个体α对应的控制参数;A2和C2为灰狼个体β对应的控制参数;A3和C3为灰狼个体δ对应的控制参数。 由于DE算法是一种全局寻优效果极佳的进化算法[14],在求解非连续、多峰值等复杂优化问题时有着较好的优化效果,常被用来与其他智能优化算法进行混合来改进算法的优化能力,因此,本文将DE算法融入GWO算法中,借助DE算法的全局搜索能力来提高GWO算法的优化精度和搜索效率。DE算法的基本原理及数学模型如下。 3.2.1 变异操作 变异操作是使DE算法能够拥有极强的全局搜索能力的核心步骤。差分变异策略有很多种,本文主要采用DE/rand/1的变异操作。 式中:Vi,g为经变异操作后的个体位置;Xa,g,Xb,g和Xc,g分别为随机从当前种群中选择的个体位置;Fr为缩放因子,其主要控制变量缩放偏差,取值范围为[0, 1]。 3.2.2 交叉操作 DE 算法采用交叉操作来增加种群的多样性,即控制新生个体加入原始种群。本文采用二项式交叉策略实现交叉操作。 式中:Ui,g+1为经交叉操作后的个体位置;Cr∈[0,1],为交叉概率;J为当前维度;jrand为随机选择的维度。 3.2.3 选择操作 选择操作采用贪婪算法的选择方式,通过将新产生的子代个体与父代个体进行比较,选择两者之中更优的个体进入下一代种群,这种选择方式可以保证下一代种群优于当前种群。 式中:Xi,g+1为经选择操作后的个体位置。 众多学者研究发现,GWO算法虽然具有优化精度高、收敛速度快的特点,但在单独求解复杂优化问题时容易出现提前收敛[15−16];而DE 算法的全局搜索能力强,但其性能对参数较敏感,且易陷入局部最优[17−18]。为了发挥二者在寻优过程中的优点并克服其各自缺陷,本文提出一种DE−GWO混合优化算法,其主要原理是在GWO算法对种群个体位置不断迭代更新的基础上,加入DE算法的变异、交叉、选择操作,进而维持种群的多样性,以便提高其搜索能力和优化性能。 DE−GWO算法的具体流程如下。 Step 1:设置优化算法中的种群规模N、迭代次数Tmax、寻优维数d、交叉概率以及缩放因子上下限等相关参数,初始化父代种群、突变种群和子代种群; Step 2:计算父代种群每个个体的适应度函数值,并进行降序排列,将目标函数最优值、次优值、次次优值对应的3 个搜索个体位置记为Xα,Xβ和Xδ; Step 3:根据式(11)和(12)更新参数A,C和a,然后通过式(13)~(15)计算种群其他搜索个体与位置Xα,Xβ和Xδ之间的相对距离,并不断更新当前搜索个体的位置,产生新一代的父代种群,并计算新种群个体的适应度; Step 4:通过式(16)产生变异种群,通过式(17)的交叉操作产生新的子代种群,计算新子代种群个体的适应度,然后,经式(18)的选择操作,选出父代种群和子代种群更优的个体进入下一代种群; Step 5:更新种群的最优目标函数值,确定新的Xα,Xβ和Xδ; Step 6:不断进行迭代计算,若当前迭代次数t 本文基于矿井智能控制实验平台进行实例分析,该实验平台主要参照某矿通风网络拓扑结构搭建而成,其通风网络设计模拟“一矿两面”结构,通风网络巷道为上下两层对称结构。实验平台的通风网络拓扑结构如图1 所示。由图1 可见:该通风网络共有15 个节点(分别编号为节点①~○15),21条分支(分别编号为1~21),独立回路数为7条,通风机位于分支20 上,通风机风压特性曲线为:Hf= 2 897.93+ 17.24Q- 0.5Q2(Q为风机风量)。图中箭头方向表示分支风流流向,出风节点○15与进风节点①之间的伪分支21 使用虚线表示,伪分支21的风阻为0 N·s2/m8。 图1 通风网络拓扑结构Fig.1 Ventilation network topology 在该实验平台中,本文构建矿井远程应急调风与智能控制系统,如图2所示,其主要包括井下分布式通风环境参数监控分站、以太网通信模块、地面远程监控中心和风量智能调节装置。基于该实验系统,本文所提智能应急调风方案的实施步骤如下: 图2 矿井远程应急调风与智能控制系统Fig.2 Disaster remote emergency wind regulation and intelligent control system 1)在井下布置监控分站来采集各巷道的通风环境参数,包括风速、风压、甲烷和烟雾浓度等。 2)井下监控分站将采集到的数据通过以太网通信协议上传到地面监控中心,并在上位机的监测界面进行终端显示;若监测系统发现甲烷浓度或粉尘浓度超限,并经决策平台确定为异常情况时,则会立即启动远程应急调风操作;工控机会将收集到的数据通过OPC 协议发送到Matlab 中,Matlab 经风网解算、灵敏度矩阵的求解、智能优化算法的迭代寻优等步骤得到最优的可调分支集,并反馈到监测系统中。 3)根据最优的调控方案,通过PLC 控制器对井下相关分支的风门、风窗等调节装置进行精准控制,使得灾变分支的风量能够快速满足应急需风要求,从而实现了多分支联合调阻增风的目的。 地面远程决策平台是应急调风与智能控制系统的重要组成部分之一,该平台通过分析通风系统目前的状况来指导和控制下一步操作。决策平台可以通过分析煤矿瓦斯监测数据来实现较为准确的瓦斯浓度预测,其实现方法主要参照文献[19]中的瓦斯突出预测预警方法,该方法选用霍尔特指数平滑法对实时监测的瓦斯体积分数进行预处理,并基于BP神经网络模型来提取监测的瓦斯体积分数的特征参数,结合人工检测的防突检测参数,构建瓦斯突出预测预警模型。现场实践表明,该方法能够较好地处理瓦斯监测数据,突出预测预警结果可靠性高。虽然上述方法对瓦斯超限预测预警的结果比较准确,但并不能完全预测到所有的瓦斯超限情况,因此,对于极少数未被预测到的情况,可以在发现瓦斯浓度超限并确定为真实异常情况下,通过矿井应急调风系统快速地将瓦斯浓度降到安全浓度以下,保证矿井生产安全。经实验平台的大量验证,上述2种方法的结合能够满足实际应用需求。 假设该通风网络中分支14发生瓦斯浓度超限,急需通过调阻增风的方式来增大分支14 的风量,下面通过求解得出分支14 的风量可调范围。表1所示为初始通风网络参数。 表1 初始通风网络参数Table 1 Initial parameters of ventilation network 本文基于Matlab 自制的计算通风网络灵敏度矩阵程序,得出不同分支调阻对分支14 风量的灵敏度,如表2所示。 表2 所有分支风阻对分支14的灵敏度Table 2 Sensitivity of all branch wind resistances to branch 14 若通过增阻调节的方式来增大Q14,则需选择可调分支中灵敏度d14,j的分支进行调节。按照分支灵敏度的影响权重从大到小顺序排列为分支12,17,15,7,13,4 和8。由于分支15,7,13,4和8 的灵敏度相对于分支12 和17 的灵敏度过小,对调风的贡献度不足,且考虑到减小调风量对风网工作状态的影响程度,选择分支12和17作为最优的可调分支集。 对选出的调阻分支12,依次计算其风阻被设定为0.42,0.52,0.72,0.92,1.12,1.32,1.82,2.32,2.82,3.82,4.82,5.82 时的灵敏度,对这12 组样点数据通过Matlab 软件中的Power 幂函数拟合处理得到灵敏度d14,12随风阻R12变化的曲线,如图3所示。 图3 灵敏度d14,12随风阻R12的变化Fig.3 Variation of sensitivity d14,12 with wind resistance R12 由此可求得灵敏度d14,12与风阻R12的关系:d14,12= 1.141R-1.16412。通过上述方法,也可求出灵敏度d14,17与风阻R17的关系:d14,17= 0.861R-1.36217。由此,根据式(7)可求出分支12 和17 对Q14进行增阻调风的合理范围:R12∈[0.42, 3.04] N·s2/m8,R17∈[0.30, 1.63]N·s2/m8。 对分支14 风量调节的最优可调分支集和风阻调节范围确定后,采用DE 算法、GWO 算法、DE−GWO 算法分别对该分支风量进行寻优,确定分支14 可调风量的最大值。主要参数设计如下:设种群规模为20,优化变量维数为2,进化迭代150 次,交叉概率Cr=0.2。为了避免寻优效果存在偶然性,同时也为了证明DE−GWO算法在优化过程中的稳定性,采取3 种算法分别对模型优化30次,优化结果见表3。从表3可以看出,DE−GWO算法的收敛速度虽然不如GWO 算法和DE 算法的收敛速度快,但其寻优效果优于GWO 算法和DE算法的寻优效果,表现出更强的搜索能力,有效地避免了局部最优。不同算法所得分支14 风量某次优化效果如图4 所示。由图4 可见,相对于DE算法和GWO 算法而言,使用DE−GWO 算法对风量调节优化的效果更好,对分支14 的最大调节风量可达8.51 m3/s。 表3 不同算法优化结果Table 3 Optimization results of different algorithms 图4 不同算法所得分支14风量适应度曲线Fig.4 Branch 14 air volume fitness curve obtained by different algorithms 当分支14的风量通过增阻调节到最大值时(即Q14= 8.51 m3/s),此时的R2= 2.48 N⋅s2/m8,R17=0.63 N⋅s2/m8,通过风网解算可求得其他各分支的风量,见表4。经对比发现,调风后的其他各分支能够满足最小需风量合理分配的要求,由此得到分支14 风量可调范围为[5.46,8.51]m3/s,风量可上调55.9%。 表4 优化调节后各分支风量分配Table 4 Air volume distribution of each branch after optimal adjustment 根据上述理论分析,下面使用矿井智能控制实验平台进行实例验证。假定监测到井下分支14的瓦斯体积分数为1.5%,经地面监测中心的决策平台判定为瓦斯浓度超限后,需启动应急调控系统。计算得出分支14 最小需风量为7.96 m3/s(瓦斯体积分数稀释至1%)。由于使用单分支调节时,分支14 的最大可调风量为7.19 m3/s,不满足分支14的需风要求,所以,可采取多分支联调的方式。由本文4.2节可知,对分支12和17进行联调增阻时,最大风量可调至8.51 m3/s,符合本次调风范围。经Matlab 风网解算后可知,当R12=1.82 N⋅s2/m8,R17=0.58 N⋅s2/m8时,分支14的风量为8.04 m3/s,此时,矿井应急调控系统通过PLC 控制器调节分支12 和17的风门或风窗开度,使分支12和17的风阻达到预设值。经应急调控操作后,分支14 的风量满足该分支的应急增风要求。 1)本文提出的DE−GWO 算法克服了GWO 算法易陷入局部最优以及易提前收敛的缺陷,提高了算法在迭代过程中的全局搜索能力,在寻优性能和稳定性方面都得到了显著提高。 2)通过分支风量期望值来选择不同调节分支的智能应急调风方案是可行的,既能保证调风经济性和矿井安全生产要求,又能满足用风分支的需风量,可快速将有毒有害气体从井下排出。
2 风量调节的数学模型
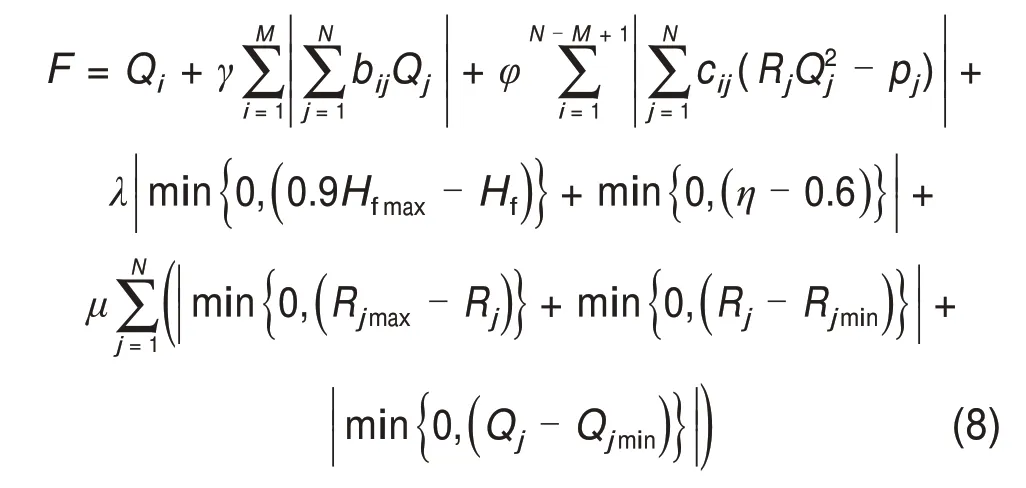
3 灰狼优化与差分进化混合算法
3.1 灰狼优化算法


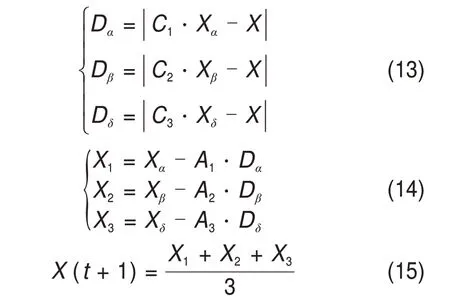
3.2 差分进化算法(DE算法)



3.3 DE−GWO算法优化流程
4 风量调节的实现


4.1 风量调节分支优化选择


4.2 风量调节优化结果分析



4.3 实例验证
5 结论
