人与结构竖向动力相互作用研究进展及展望
2022-01-07李俊兴张文元丁玉坤杨奇勇
李俊兴,张文元,丁玉坤,杨奇勇
(1. 哈尔滨工业大学结构工程灾变与控制教育部重点实验室,黑龙江哈尔滨,150090;2. 哈尔滨工业大学土木工程智能防灾减灾工业和信息化部重点实验室,黑龙江哈尔滨,150090;3. 北京国家游泳中心有限责任公司,北京,100101)
人群激励荷载下的结构振动不仅影响结构安全,而且影响舒适度。例如,2000 年,英国千禧桥[1]开放当日,大量人群在桥上行走,引起剧烈振动。日本T 桥[2]在大量人群通过时产生剧烈振动并且有约20%的行人与桥梁同步振动。2011 年,韩国Techno Mart 大楼[3]因健身房学员做健身操而持续振动10 min,引起人群恐慌性逃离。这是由于结构自振频率与人致荷载主要频率相近,引起结构过度振动,人感知到结构振动并产生生理和心理上的变化。近年来,张文元等[4]提出了一种钢木组合的冰下支撑结构形式,可随时将水立方的游泳场馆临时转换为冰上项目场地。相比建立在夯实地基上的传统冰场,该可拆卸冰场刚度小,钢木组合结构质量小,这些因素引起的人致振动是转换冰场设计时需要考虑的一个问题,同时,荷载下冰面的竖向振动和变形也值得关注。因此,人与结构的相互作用问题也存在于人与新型转换冰场中。传统的结构设计仅考虑人致荷载或者将人作为结构上的附加质量,忽略人体动力特性,直到英国千禧桥事件发生后,越来越多的学者注意到人与结构的相互作用问题,将人作为动力系统看待,并对人和结构耦合形成的新动力系统展开了研究。
人与结构的相互作用一方面指人对结构动力特性和结构响应的影响;另一方面,指结构振动对人的作用,即结构振动对人体动力特性、人运动方式和人致荷载的影响。随着现代结构向大跨方向发展以及轻质高强建筑材料的广泛应用,结构柔性越来越高,人与结构相互作用问题越来越受到人们的关注。本文从人致荷载、人体相互作用模型、人对结构动力性能的影响、结构振动对人的影响这4个方面出发,介绍人与结构竖向动力相互作用研究中的重要概念和研究进展,并从振源、传递路径、振动接收者3个方面展望未来的研究方向。
1 人致荷载
人类各种活动引起的激励是结构振动的重要来源之一,直接影响结构的安全性和舒适性。人们对人致荷载的研究主要包括荷载测量方式和数学建模两个方面。人致荷载包括单人荷载和人群荷载。在结构设计及性能评估时,人群荷载比单人荷载重要。对于人群荷载,尚未出现公认有效的试验技术[5],因此,人群荷载实验数据较少。另外,由于个体间的差异性以及人与人的相互作用问题,人群荷载并不是简单地将单人荷载叠加,其取值是一个复杂的问题。下面对单人荷载研究结果进行总结与讨论。
1.1 荷载分类
根据建筑使用者活动的不同,人致荷载可以分为步行荷载、跑步荷载、屈伸荷载、跳跃荷载、摇摆荷载、跺脚荷载、突然站立/坐下荷载等。不同活动产生的荷载幅值和频率不同,如表1所示。

表1 常见人致荷载类型[5]Table 1 Classification of human-induced loads[5]
1.2 荷载测量方法
1.2.1 直接测量方法
结构振动的激励力来源于脚和结构的接触力,因此,根据牛顿第三定律中作用力与反作用力关系,人致荷载也可视为地面接触反力(ground reaction force,GRF)[6]。最常用的荷载测量方法是通过带有力传感器的测力板直接测量GRF,这种测法简单准确,但由于受测力板尺寸限制,多用于获得单步时间−荷载曲线,再通过增加测力板的数量得到有限连续步荷载曲线。随着技术发展,人们将跑步机与测力板结合起来,并使用这种带有力传感器的跑步机测量GRF。这种方法可以测量连续步的行走荷载、跑步荷载。这2种测量方法限于实验室环境约束,不能原位测量,并且测力板的尺寸和位置会影响人的运动,人在测力板和跑步机上的运动状态与正常无约束运动状态有区别。然而,带有压力传感器的生物测力鞋垫克服了以上测量仪器的不足,通过对足底压力面积积分便可得到脚与鞋垫的接触力。该方法摆脱了人工实验室条件限制,可以原位测量,但由于足底压力测量系统、温度、弯曲、剪切、运动类型等的限制[7−8],该方法与前面2种直接测量方法所得结果差别较大。另外,使用生物测力鞋垫只能测得竖向荷载,不能得到人致荷载水平方向上的分量。
1.2.2 间接测量方法
人致荷载的间接测量方法是指通过获得其他物理量来反推算出荷载的方法。间接测量方法主要包括以下2类:一类是根据测量所得的结构响应逆运算得到人对结构的荷载时程,属于结构的反问题。刘军进等[9]在混凝土板下设高频力传感器,得到单步落足荷载曲线和跳跃荷载曲线。另一类方法基于牛顿第二定律,认为身体各部分的质量与加速度的乘积之和等于任一时刻的地面接触反力[6]。这种方法忽略软组织变形的影响,假设人体由一连串的刚性体段组成[10],在知道人体质量分布的前提下,使用有标记点的光学运动捕捉技术[10]、视频运动捕捉系统[11]、无线惯性传感器[12−14]等获得人体各部分的加速度从而间接测量荷载。该方法可以实现原位测量,没有行走路线约束,可以测得连续荷载曲线。
人致荷载的直接测量方法简单,荷载结果通过传感器直接传出,间接测量法则需要获得较多的已知数据和大量计算。基于运动捕捉的间接荷载测量方法有助于研究人群荷载特性,揭示人与人之间的相互作用,是研究人群荷载取值及荷载时空特性的有效手段,有广阔的应用前景。
1.3 荷载模型
ZIVANOVIC 等[15]认为数值模拟人致动力荷载是一项复杂的任务,主要原因如下:1)存在不同类型的人致荷载,其中一些荷载在时间和空间上都发生变化;2)荷载取决于许多参数(步频、步速、接触时间、步长等);3)单人产生动力荷载是一个窄带随机过程,因此难以建模;4)人数及其同步(行人间同步)程度的影响难以概括;5)在可感知和不可感知的结构振动情况下的人致荷载是不同的。学者们采用不同的数学表达式(傅里叶级数、正弦/正弦平方、高斯函数、小波、功率谱等)模拟荷载曲线,并对模型参数(荷载因子和相位角)分布及取值进行了研究。
1.3.1 确定性荷载模型
确定性荷载模型简单地将人的活动视为一个周期重复的过程,将产生的荷载看作周期性荷载,以傅里叶级数形式表征。以竖向步行荷载FZ(t)为例[16],

式中:G为人的静止重力;αZi为竖向第i阶傅里叶系数,也称为动载因子(dynamic loading factor,DLF);fp为人的步行频率;φZi为竖向第i阶谐波相位角;n为模型中考虑的阶数。
对于步行的情况,上述荷载模型忽略了左右脚交替落地行走时空间作用点的变化。BLANCHARD 等[17]认为采用连续步荷载模型将步行荷载表达为空间上的连续力虽然与实际空间离散作用点不一致,但对于大跨结构和低频模态是适用的。为了更真实地反映荷载空间离散性,消除荷载作用点离散对预测结构响应的影响,樊健生等[18]基于行人步行竖向荷载特征,构建了标准单步落足荷载曲线模型并验证了模型的准确性。
人体活动是一个随机过程,存在个体间的差异性(inter-subject variability)和个体内的差异性(intra-subject variability),不同的人做同样的运动,产生荷载不一样,同一人不同落脚时刻产生的荷载也有差异。确定性荷载模型基于周期性假设,将荷载能量集中在整数倍步频或跳跃频率处,从而高估了共振情况下结构响应,低估了高频结构响应[19]。
1.3.2 随机性荷载模型
随机性荷载模型能够准确预测结构响应,更适合描述人致荷载。随机性荷载模型可分为基于确定性模型的随机模型、功率谱模型和基于机器学习的随机荷载模型。
在确定性荷载模型的基础上,根据模型控制参数的分布规律随机取值,进而得到随机模型。这种荷载模型具有真实荷载的窄带随机特性,但忽略了荷载高频部分的能量。
考虑到人体运动是随机过程,也可以使用功率谱模型(power spectral density,PSD)描述荷载的随机性。近年来,随着人工智能的发展,输入真实样本曲线,通过机器学习训练也可获得具有真实荷载特征的模拟荷载。
陈隽等[20]将接触率和跳跃频率作为2个独立随机变量,按照试验数据分析给出的变量概率分布特性,随机取得荷载模型参数,以半正弦和半正弦平方函数作为不同跳跃频率下的脉冲荷载曲线模型,并在此基础上模拟随机跳跃荷载曲线。XIONG 等[19]基于大量跳跃荷载试验数据,用功率谱模型表征个人跳跃荷载,并对比随机振动理论预测的结构响应与实测结构响应,验证了该模型的有效性。XIONG 等[21]采用生成式对抗网络来模拟步行、跳跃、屈伸等荷载,且模拟出的荷载曲线与实测荷载曲线相近,功率谱密度及结构响应也与实际情况一致。
2 人体相互作用模型
人体是一个非常复杂的非线性动力系统,人体模型对于研究人与结构相互作用必不可少。学者们对站立、步行人体模型进行了大量研究,并研发出很多生物学人体模型,包括单自由度模型和多自由度模型。让人站立或坐在振动台上,测量人−结构系统在驱动点处的受力和响应,然后计算驱动点处的频率响应函数(frequency response function, FRF),通过拟合测量所得频率响应函数来确定这些模型的质量、刚度和阻尼[22]。
2.1 质量−弹簧−阻尼(MSD)模型
此前,学者们在研究人对结构动力特性的影响时,仅将人看作是附加在结构上的质量块,这样能够解释结构频率降低的现象,但不能解释结构频率增大、阻尼增加以及出现新增模态的现象。受生物力学研究启发,学者们开始采用质量−弹簧−阻尼(mass−spring−damper,MSD)模型作为人体模型,如图1所示(M,K和C分别为模型质量、刚度和阻尼)。

图1 MSD模型[22]Fig.1 MSD model[22]
根据自由度的不同可以分为单自由度质量−弹簧−阻尼模型(SDOF−MSD)和多自由度质量−弹簧−阻尼模型(MDOF−MSD)。但SACHSE 等[23]认为更复杂的模型适用于研究人体的局部运动以及振动在人体的传递过程,不适合研究人与结构相互作用。单自由度的MSD 模型因其简单高效而得到了广泛应用。ARCHBOLD[24]使用SDOF−MSD模型模拟了单人步行过桥的竖向响应,并将其结果与仅考虑荷载模型结果进行了比较。DANG等[25]发现在轻质结构中,由于人与结构相互作用显著,传统的仅考虑人致荷载的模型不能预测结构响应,而MSD人体模型可以较好地预测结构响应。
为了研究移动人体与结构的相互作用,考虑行人空间变化对结构的影响,FANNING 等[26]将傅里叶简谐力加在移动的MSD 模型上,以表示结构上的行人,研究行人与结构相互作用。CAPRANI等[27]全面介绍了带移动荷载的MSD人体模型(见图2)并推导出其与结构相互作用的方程,可用于有限元分析。

图2 移动MSD模型[27]Fig.2 Moving MSD model[27]
需要注意的是,不同姿势、不同振动强度下的人体模型参数不同。ALEXANDER[28]认为在各种姿势下,人的自然频率变化范围为1~16 Hz,人体阻尼比变化范围为0.3~0.5,故生物力学研究得到的模型参数不能直接应用于土木工程结构振动研究中。SILVA等[29]通过步行力和腰间记录加速度的相关性识别出SDOF−MSD模型参数,并给出了3 个参数的经验公式,但缺少真实结构实验验证。ZHANG 等[30]通过拟合不同数量行人作用下后张混凝土桥频率响应函数和模拟结果,计算得到模型参数。ZIVANOVIC[31]通过拟合行人过桥试验所得结构峰值响应和模拟结果,得到行人频率和阻尼范围。SHAHABPOOR等[32]考虑步行荷载和振动器荷载对结构动力特性的影响,使用基于个体(agentbased)模型模拟行人与桥梁竖向相互作用,由结构模态参数逆向工程法得到人体模型参数。WEI等[33]从人与结构耦合系统测量所得频率响应函数识别出单人站立姿势和蜷伏姿势动力特性和结构的动力特性,但目前该方法尚不能应用于多人与结构耦合系统中子系统动力特性识别。
2.2 连续体模型
因为人体是连续的,故使用连续体模型表示站立人体是合理的[34]。JI[34]使用由上下两段不同质量和刚度的段体组成的连续体模型(图3(a))来模拟人体站立姿势下的竖向振动。该模型通过叠加部分单自由度系统响应来计算人体响应,需要确定的未知量比离散体模型的少。ZHANG[35]利用生物力学模型中的2个固有频率,对模型中的质量分布进行拟人化处理,改进了竖向振动环境中的站立连续体人体模型(图3(b))。ZHANG[35]确定了连续体的模态特性,并将其与离散体模型的模态特性联系起来,发现沿体长分布的刚度对精确模型的影响比质量对模型的影响更大。ZHOU 等[36−38]在文献[34]中所提模型基础上,进一步通过试验和理论分布,改进了连续体模型,并应用于人与结构的相互作用研究中,分析结构振动对人体模型动力参数的影响。
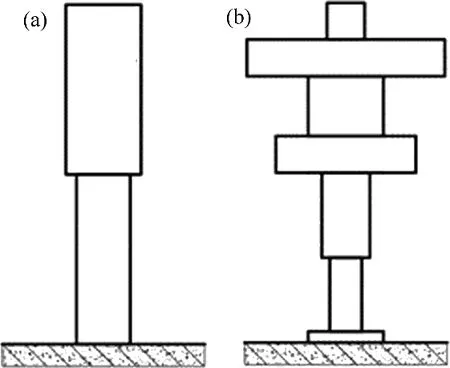
图3 连续体模型Fig.3 Continuous body models
连续体模型难点在于合理确定沿体长分布的质量、刚度、阻尼等参数,且连续体模型多用来表示站立姿势下的人体模型,应用较少。
2.3 倒钟摆模型
倒钟摆模型将人体简化为质心,并由2个无重刚性杆件支撑。人的双足倒钟摆模型最初被用于研究步态详细信息,比如步频、步长、身体质心的运动、脚跟落地的时刻、脚趾离地的时刻。倒钟摆模型对人与结构相互动力作用的模拟效果更好,并且可以反映结构振动对结构上的人的运动状况的影响[39],因而得到了较广泛应用。
QIN等[40]使用具有阻尼柔性腿的双足倒钟摆模型来模拟行人,研究了腿部刚度和阻尼以及前腿的冲击角度对结构响应的影响,发现当步频接近结构固有频率时,腿的刚度对结构的动力响应影响显著。双足步行模型原理如图4 所示(其中θ0为冲击角)。WHITTINGTON 等[41]将滚轮脚纳入双足模型来模拟人行走,该模型可以更精确地模拟人行走时的双足支撑阶段。YANG等[42]提出了一种具有柔性腿的三维人体双足步行模型,该模型用时变阻尼器模拟人的腿,使用较少的参数即可描述步态模式。王益鹤[43]基于ISO 5982[44]模型与双足模型,建立了2DOF双足模型,研究了该模型的力学特性和稳定性,并使用该模型研究了人与结构相互作用。

图4 双足步行模型原理[40]Fig.4 Schematic of biomechanical walking model[40]
倒钟摆模型比单自由度MSD 模型复杂,需要确定更多的参数,尤其是研究人群与结构相互作用时,其计算量较大,不适合用于日常设计;此外,该模型需要进行大量假设,缺少实验数据验证。
2.4 多链杆模型
为了解决机器人建模中的行走问题,ADDI等[45]建立了双足人体运动系统多链杆模型(图5),模拟所得的双足地面接触反力呈现出M 型双峰特点,与真实荷载曲线形式吻合。VAMPOLA等[46]使用带有正负反馈的三维多体步行模型研究行人与桥在竖向和水平向的相互作用,发现桥的动力响应受步频与结构频率之比的影响。

图5 双足多链杆人体运动模型[45]Fig.5 Multilink−segment biped locomotion model[45]
与倒钟摆模型相同,多链杆人体运动模型能够反映运动过程中的更多细节,适合模拟单人与结构相互作用。但该模型为多自由度模型,且需要的输入参数和维持步态稳定的控制假设更多。
本文从接触力、自由度数、维稳控制方程、步态特征、适用范围及活动这几个方面比较上述4种人体相互作用模型,如表2所示。

表2 相互作用人体模型比较Table 2 Comparison of human models for human−structure interaction
3 人对结构动力性能的影响
结构上的人不仅会提供激励荷载,还会与结构产生相互作用进而影响结构的动力特性和动力响应。此前,人们仅考虑人致荷载或仅将人作为结构上的附加质量,导致结构响应被高估,且无法解释结构动力特性的变化。ELLIS 等[47]对Twickenham体育馆的悬臂看台进行动力测试发现,当看台布满人群时,相比于空载情况,结构多了一个模态。ELLIS等[47]将人群和结构作为两自由度动力系统进行了理论分析,最后通过试验验证了该理论分析的正确性。
学者们认识到人与结构相互作用的重要性后,针对不同活动下(站立、行走、跑步、跳跃)的人对不同结构(楼板、楼梯、看台、人行桥)的影响进行了研究。
已有研究表明,站立、行走、跑步等运动与结构间存在相互作用。由于跳跃时双脚和地面接触时间短,ELLIS等[48]认为跳跃运动下结构的动力特性不会受到影响,但对于人群跳跃的情况,因无法保证脚能够同时离地,仍需要考虑人与结构的相互作用。GASPAR等[49]通过试验和数值模拟研究了单人跳跃运动与活动楼板间相互作用,其结果表明,与不考虑人体动力性能的跳跃荷载模型计算所得结构峰值加速度响应误差(192%)相比,考虑相互作用的模型响应误差(−14%)更小,建议楼板设计时考虑跳跃运动与结构的相互作用。
针对楼板、楼梯、看台、人行桥等低频柔性结构,已有较多研究,学者们可根据频率判断是否需要考虑相互作用,即低频结构需要考虑相互作用,高频结构无需考虑相互作用,但针对高频与低频结构的截止频率尚未有明确的结论。当结构频率大于10 Hz时,在人与结构质量比不大的情况下,建议不考虑人与结构的相互作用,仅采用人致荷载计算结构响应[50]。
3.1 人和结构耦合控制方程
以J人驻留的梁为例,考虑梁的N阶模态,使用模态分析法分别介绍不同人体模型作用下的耦合方程。
3.1.1 MSD模型
矩阵形式的控制方程[27]为

式中:M,C,K,Q(t)和q,分别为广义质量矩阵、阻尼矩阵、刚度矩阵、广义力向量和位移向量。
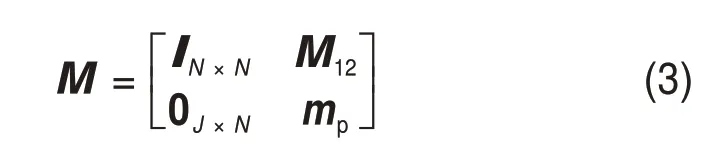

3.1.2 连续体模型
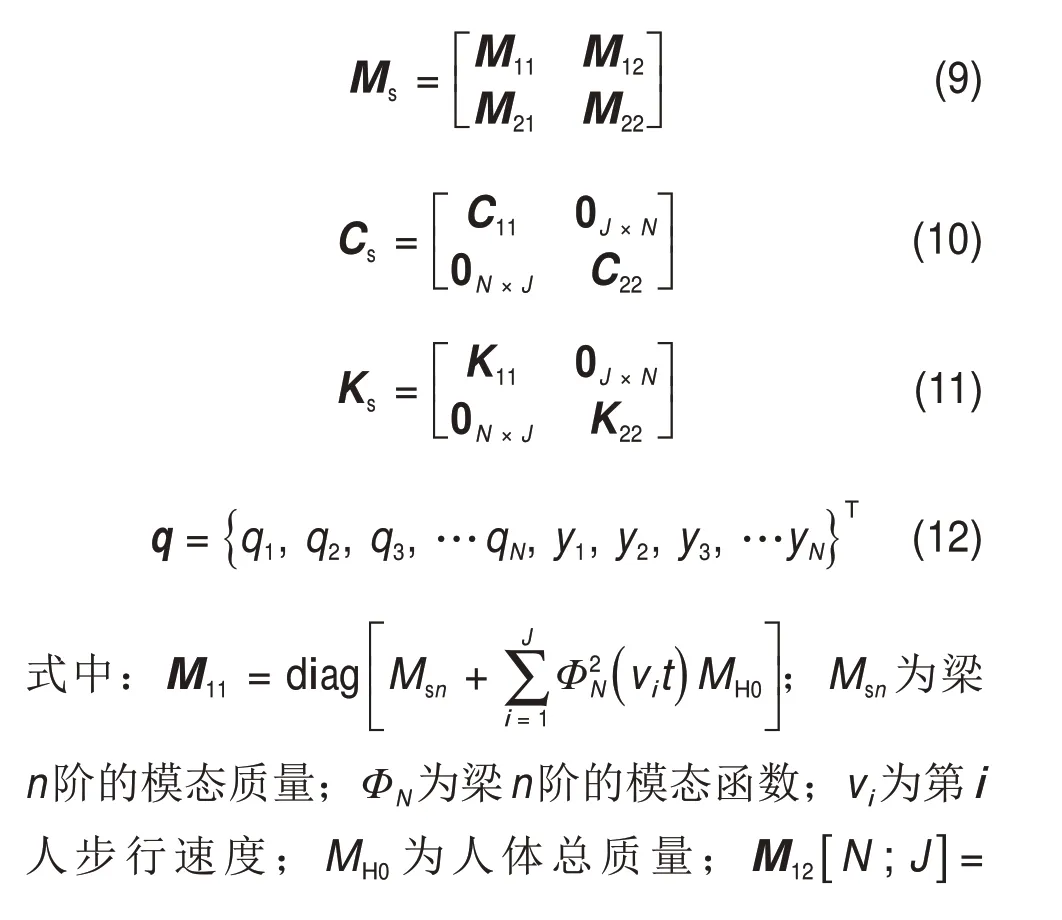
耦合体系自由振动控制方程[51]为

式中:Ms,Cs,Ks和qs分别为连续体模型中广义质量矩阵、阻尼矩阵、刚度矩阵和位移向量。

3.1.3 双足模型
近年来,GAO等[52]在文献[40]中所提模型的基础上改进了双足模型,提出人群与结构相互作用模型,并采用社会力学模型来研究人与人之间的相互作用,但未通过试验验证模型的有效性。
3.2 人对结构动力特性的影响
人体阻尼非恒定值,在不同运动、不同姿态下阻尼不同,应视为重频阻尼动力系统。结构上人体会(被动或主动)吸收结构振动能量,增加结构的阻尼。BROWNJOHN等[53]研究了人−板耦合系统振动,发现人体会吸收部分能量,起到提供阻尼的作用,人体姿势对结构阻尼有影响,屈膝能提供耦合系统更多的阻尼。SHAHABPOOR等[54]发现行走人群也会增加结构阻尼比,并且行走状态下的结构阻尼比大于同样位置处站立姿态下的结构阻尼比,即行人给结构提供更多阻尼。但是限于试验人数,结构阻尼比增大与人数增大的关系尚不清楚。HE 等[55]设计了竖向基本自振频率为2.4 Hz 的人行桥模型,研究静态和动态人群数量对轻质柔性桥阻尼变化的影响,结果表明随着人数增加,结构阻尼比增大,当达到一定人数时,阻尼比趋于稳定,该结果与理论模型结果一致。
ZHANG 等[56]针对上人轻质钢楼板的振动特性展开了试验研究,发现人可使楼板振动频率增加,而与人等质量的家具则使楼板振动频率降低。SALYARDS 等[57]通过可调节频率的悬臂看台研究了不同结构频率、不同人与结构质量比、不同站立姿态下人群与结构的相互作用,发现相互作用影响了耦合系统的结构频率。SALYARDS 等[58]在评估用于相互作用人群模型的动力参数时发现,对于直立和坐姿人体,在人与结构质量比较小的情况下,楼板一阶竖向频率稍增大。然而,随着人与结构质量比增大,结构频率显著减小;但是对于屈膝站立的人群,结构频率随着人与结构质量比增大而增大。BUSCA 等[59]现场测量了不同数量、不同位置站立人群下的楼梯频率,并与不站人时楼梯的频率比较,发现由于站立人群的存在,细长楼梯的频率相比空载时的频率稍稍降低。ZIVANOVIC 等[60]研究了不同人数站立或行走下结构的动力特性,发现随着站立人数增加,结构频率降低;随着行走人数增加,结构频率增大(图6)。

图6 不同人数站立或行走作用下结构动力特性的变化[60]Fig.6 Changes of structural dynamic characteristics under different standing or walking conditions[60]
以上结果表明,人既能使结构频率降低,也能使其频率增加,这取决于人体基频与结构基频的相对关系。SACHSE等[61]在研究两自由度人群与结构相互作用时,通过参数变换模拟结构频率降低或增大,发现在空载结构频率fS和人体频率fH的一般变化范围内,当fS
3.3 人对结构动力响应的影响
将人看作是作用在结构上的MSD 动力系统,人与结构接触面处的振动激起人体运动,从而产生作用力并反作用在结构上,最后影响结构振动响应。有研究表明,结构阻尼因人与结构的相互作用增大,相比于不考虑人与结构相互作用的情况,考虑相互作用时结构响应强度明显降低。
DA SILVA 等[63]在人群过桥所致的动态响应研究中,分别采用现行规范推荐的移动荷载模型和移动生物动力学模型模拟行人运动引起的结构响应,并将其与人行桥上人群行走试验测得的加速度进行对比,结果表明移动荷载模型所得结构响应偏大,而生物动力学模型因包含人与结构相互作用,模拟结果与试验结果较一致。SHAHABPOOR[64]提出基于相互作用的步行振动舒适度评估方法,该方法考虑了人体模型参数的随机性和步行荷载个体内与个体间差异性,并给出了结构响应发生的概率。其研究结果表明,采用考虑相互作用方法模拟所得加速度响应与试验结果最大相对误差为5%~10%,远小于不考虑相互作用时所得最大相对误差(100%~200%)。但是,该方法还需要验证完善以适用于不同结构和不同荷载情况。VAN NIMMEN 等[65]在不同人流密度和不同桥梁参数下对结构响应进行数值模拟,发现与仅考虑人致荷载的工况相比,考虑人与结构相互作用使桥梁的加速度响应降低,高人流密度下的加速度响应至少降低30%。
然而,BASSOLI 等[66]通过参数分析发现,人与结构相互作用对桥梁最大响应的影响主要取决于结构自身频率,当桥梁频率约为2 Hz 时,在一定人群密度范围内,考虑人与结构相互作用时耦合系统最大加速度大于不考虑人与结构相互作用时桥梁的最大加速度(图7)。

图7 不同人流密度下桥梁跨中最大加速度响应[66]Fig.7 The maximum acceleration response of bridge midspan under different pedestrian density[66]
杨康[67]认为运动人体可简化为移动MSD系统,考虑人和梁耦合作用时,人群对梁加速度振动响应有一定的影响。杨康[67]通过试验板的测试发现,与质量块相比,人体不仅能够降低结构振动响应,而且能加快结构振动响应的衰减。何浩祥等[68]基于不同姿势下的人体动力模型,建立人与10 层住宅耦合的动力系统,研究不同人数、不同姿势下人与结构的振动加速度响应,发现随着人数增加,结构的减振效果越明显,坐姿人体受竖向环境振动的影响最大。
4 结构振动对人的影响
人可看作是一个具有自适应能力的动态系统,其行为受社会、心理、生物力学和环境等多种因素综合影响,感知结构振动并对其做出反应。结构的振动会影响到人的运动状态。另外,人的腿部关节刚度会在受到振动干扰时增大,对振动刺激做出反应[69],从而引起人致荷载以及人体动力参数变化。
4.1 对人致荷载的影响
人致荷载受接触面刚度影响,柔性接触面上的动力荷载小于刚性面上的动力荷载。
YAO 等[70]通过实验研究发现跳跃荷载接触比(每次跳跃触地时间与跳跃周期的比值)随着平台频率增大而减小,刚性平台上跳跃荷载幅值大于柔性平台上荷载幅值。
AHMADI 等[71]通过压力鞋垫获得刚性地面和柔性桥面上单人步行荷载,并研究了结构振动对步行荷载的影响,发现在共振(步频等于人行桥频率)时柔性桥面上的一阶动载因子小于刚性地面上对应的动载因子,并且随着步频与结构频率比以及人体与结构质量比减小,一阶动载因子差异变小,即结构振动的影响不显著。
DANG等[72]在研究低频结构振动对行人运动影响时证实了自激力(self-excited force,SEF)的存在,即振动结构上产生的接触力不仅在整数倍步频处含有简谐分量,而且在结构自振频率处也存在分量。试验结果表明自激力通常随振动强度增大而增大,与步频和结构自振频率的比值关系不大。
CAPPELLINI等[73]将竖向振动结构上的接触荷载F分为被动地面接触反力(passive ground reaction force, PGRF)和主动地面接触反力(active ground reaction force,AGRF)2 个部分,其中PGRF 是由结构振动引起的,取决于人的动力特性和结构的振动;AGRF是指推动人体主动运动的力,只与人的运动有关。

式中:FP为被动地面接触反力;FA为主动地面接触反力。
何卫[50]为研究人与结构竖向相互作用对足底作用力的影响,将柔性结构与刚性测力平台上足底动荷载的差值进行归一化处理,提出相互作用影响函数D(t)的表达式:

式中:P(t)为考虑人与结构竖向相互作用时的足底动反力;fp(t)为刚性测力平台上的足底动反力;m为行人质量;g为重力加速度。
谢伟平等[74]采用文献[50]中所提相互作用影响函数,用自激励人体模型研究人桥质量比和桥梁自振频率对足底反力的影响,发现当结构频率与步频及其主谐波分量频率接近时,人与结构间相互作用最显著,其对人体足底反力影响最大。谢伟平等[75]应用双足模型发现,人与结构间的相互作用导致支撑腿产生的足底反力减小,随动腿产生的足底反力增大。
4.2 对人体模型参数的影响
由本文第2.1节可知,人体模型参数不仅取决于振动强度,还与人体姿势、振动方向有关。MATSUMOTO等[76]发现当振动强度从2.000 m/s2降低到0.125 m/s2时,站立人体振动频率从5 Hz增大到7 Hz。MANSFIELD等[77]针对竖向振动下坐姿人体的表观质量进行研究,发现当振动强度从0.25 m/s2增大到2.50 m/s2时,人体表观质量共振频率从5.4 Hz 减小到4.2 Hz。以上生物力学研究表明,人体刚度随着振动强度增大而减小。但上述研究仅通过控制振动台振动来研究被动人体(站立或坐下)的动力特性,缺少现场试验验证。
HEINEMANN 等[78]在研究步行和跑步人体动力特性时发现,当结构振动频率由1.80 Hz 变化到3.90 Hz 时,步行人体平均频率从1.39 Hz 增大到1.65 Hz,平均阻尼比由0.49 增大到0.61。这一结果与MATSUMOTO 等[76]所得结果不一致,可能是振动频率变化引起的。另外,该研究测量样本不足,结果较分散,其结论不具普适性。
GASPAR 等[49]以不同的跳跃频率激起楼面(基频为3.84 Hz)振动,研究跳跃人体与结构相互作用,并识别人体动力参数,发现随着跳跃频率变化,人体自振频率和阻尼比也随之发生改变,这从侧面说明了结构的振动会反作用于人体,使其动力特性发生变化。实际上,跳跃荷载频率的改变不仅通过共振影响结构振动响应,跳跃荷载幅值、能量集中频率的变化也会影响结构振动响应程度与频率。
杨予等[79]通过2 种不同刚度的振动台对人体5种站立姿态下的等效单自由度模型参数展开了研究,发现柔性振动台(2.73 Hz)上的人体自振频率低于刚性振动台(10.29 Hz)上的人体自振频率;而柔性振动台上的人体等效阻尼比远大于刚性振动台上的人体等效阻尼比,最大差距可达10 倍以上。杨予等[79]认为,这是由于结构主振型的变化导致人与结构耦合程度不同。值得一提的是,该试验研究仅有2位测试者,其结论不具有普适性。
结构振动对使用者的动力特性产生影响,其原因如下:一方面,在不同振动情况下,人体姿态会发生变化,导致人体参数变化;另一方面,人作为非线性生物动力系统,其动力特性与振动相关。
5 研究展望
针对结构振动舒适度,需要考虑3 个关键问题,即振动来源、路径和接收者[80]。人的各种活动产生的荷载激励结构振动,同时人又感知结构振动,故人既是振源也是振动接收者。而人−结构耦合系统作为传递路径,将振动从振源传给接收者。
5.1 人致荷载的测量及相关模型研究
当结构具有有限刚度和承载力时,准确合理地计入人致荷载对下部结构设计具有重要意义。
5.1.1 原位测量人致荷载
目前人致荷载多是在刚性平面上测量所得,没有考虑结构振动引起人致荷载降低的情况。试验室环境限制了测试者的正常运动,这也导致测得的荷载与自由运动下的荷载存在差异。使用测力鞋垫和基于运动捕捉系统的地面接触反力测量方法,摆脱了对人工环境的依赖,所测得的运动状态更接近于真实情况。但是由于存在对传感器精度要求高、测量结果精度不高、捕捉距离受限、标记点遮挡、数据同步等问题,基于运动捕捉的原位测量方法在某些情况下并不适用。VAN NIMMEN 等[81]提出将试验测试与单步荷载模型相结合的方法。该方法不依赖于信号准确度,只需要1个标记点,且标记点位置不受限制,便可构建较准确的竖向荷载。
5.1.2 三维荷载模型
实际上,人活动产生的荷载在横向、纵向和竖向3个方向都存在分量。然而,目前的荷载研究中假设3个方向荷载相互独立。结构设计和人致振动分析仅考虑荷载主要方向对结构响应的贡献,却忽略了其他2个方向荷载的影响,且未考虑不同方向荷载的耦合作用。赵丁苏等[82]通过对三向荷载耦合作用下以及仅竖向加载下的楼梯加速度响应进行分析,认为仅考虑竖向荷载分析人致振动是不合理的,而需要考虑三向荷载共同作用。
5.1.3 随机荷载模型
确定性荷载模型不能准确描述人体的动力作用,随机性荷载模型更适合描述人致荷载。另外,舒适度问题不同于强度问题,它是一个不确定问题。随机荷载模型为振动可靠度分析提供了基础。
5.1.4 其他场地人致荷载研究
传统民用建筑中的人致荷载已有较多研究,但是针对其他场地尤其是体育领域的人致荷载研究较少。随着人们对建筑功能的要求日益增加,通过转换结构实现大众不同功能需求的转换冰场、篮球馆、网球馆、舞台等将成为趋势。冰上运动荷载、体育球类比赛荷载、舞台表演运动荷载等将成为转换结构设计的关键。
5.2 人与结构耦合系统的研究
结构上的人能够增加结构阻尼,改变结构频率;当结构处于与人共振的频率范围内时,人与结构质量比越大,耦合作用越明显。但目前人与结构相互作用机理尚不明确,缺乏详细的理论和实验研究。
5.2.1 人对临时场地的影响
已有的人与结构相互作用研究多集中在楼板、楼梯、看台、人行桥等结构,对承载力和刚度有限的临时场地研究较少。例如,运动员对各类临时搭建的非传统场地的影响、表演人员对舞台结构的影响、建筑工人对脚手架结构的影响等。
5.2.2 人体参数研究与参数库建立
有关静态人体参数的研究较多,ISO 5982 中也给出了不同姿势下的人体参数。但有关运动人体模型参数的研究较少。例如,行人等效动力参数试验研究较少,有关跳跃人体模型参数的研究较少,并且目前不同研究所得人体参数差异较大。解决这个问题,对于研究人行走作用下的桥梁、大跨轻质楼板、楼梯等柔性民用建筑动力响应及舒适度有重要意义。
5.2.3 含时变参数的人−结构相互作用模型
不同于被动人群,运动过程中人体模态质量、刚度、阻尼、自身频率等参数并非恒定。因此,能够同时反映出结构振动对人体参数以及对运动过程影响的模型才更符合人与结构相互作用的特点。
5.2.4 面向工程设计的简化人群−结构相互作用模型
虽然MSD 模型、连续体模型和双足模型较好地解决了人与结构相互作用问题,但这些模型不适用于日常设计。如研发出可用于软件中的相互作用模型,通过输入人数、人体参数、结构参数等,简单操作即可模拟人与结构的相互作用从而准确预测结构响应,这将具有较广阔的应用前景。
5.3 人对结构振动的反应
人对结构振动的反应是一个复杂的问题。这是因为人感知结构振动具有个体间和个体内差异性。在同样振动强度下,不同人对振动的感知能力和反应水平不同;在同样振动强度下,同一个人在不同场合、不同状态下对振动的感知能力和反应水平也不同。另外,人感受到结构振动后,如何调整步态以维持自身稳定尚需从生物力学的角度进行深入研究。
结构振动对使用者舒适度的影响。例如,商场楼面对顾客、各类临时看台对观众、行驶的列车对乘客、桥梁对上部行驶的车辆舒适度的影响。目前人们对舒适度评价指标以及包含专业特殊人群的舒适度阈值尚未形成定论。有研究表明,相较于频率、位移等指标,用加速度来评价结构振动对使用者舒适度的影响更合理。然而,根据加速度的表达形式不同,目前舒适度常用评价方法有峰值加速度(peak accelerations,PA)、均方根加速度(root mean square accelerations,RMS)和振动剂量值(vibration dose values,VDV)3 种方法,且基于不同加速度指标评价结果相差较大。最近,GONCALVES 等[83]认为VDV 不仅考虑振动幅值,还考虑了振动持续时间的影响,更适合评价办公楼板振动。此外,由于人体振动敏感度取决于结构振动方向、频率、幅值、自身活动类型及其对振动感知模糊度,加速度权重和舒适度评价曲线应考虑上述多种因素的影响。
结构振动对处在结构上的人员专业动作的影响。例如,各类临时场地对篮球、排球或花样滑冰运动员等技术水平发挥的影响。由于目标群体的特殊性及活动的专业性,位于功能转换结构上人员对振动的感知与结构对专业动作影响的研究较少。对这些问题展开研究,将有利于提升运动员竞技比赛成绩。随着新技术的发展,运动捕捉技术、虚拟现实技术等为研究提供了较多便利。
