出平面线源荷载对半空间内椭圆孔洞的Green函数解
2022-01-07邓小环兰国冠许华南
邓小环,兰国冠,许华南
(龙岩学院资源工程学院,福建 龙岩 364012)
地下复杂结构与复合缺陷的动力学研究,在爆炸力学、地球物理学的课题研究中具有重要的工程实践意义,在地下隧道工程、地下勘探及探索、采矿和石油开采等工程领域中有非常广泛的应用。迄今为止,国内外专家对地下复杂结构和复合缺陷的研究有了很多的进展。采用复变函数和Green函数等解析方法,解决了孔洞[1-5](主要为圆形)、夹杂[6-8]和裂纹缺陷的散射问题。Qi等[9]利用镜像法、Green函数法和导波理论分析了压电双相材料带中剪切水平导波对圆孔的散射。文献[10]结合保角映射技术的应用解答了具有非均匀剪切模量的半空间中,圆形孔洞对SH波的散射问题。另外,文献[11-14]则采用数值分析的方法、基于边界积分方程法中的非超奇异牵引法等方法,研究了孔洞、夹杂与裂缝的动态响应问题。在现有的研究成果中,研究模型基本上采用规则的几何形状边界的模型,而在实际工程中,地下构造的几何形状往往不规则,分析模型多为椭圆形、三角形等,由于分析难度大,位移场更为复杂,故这类的研究报告相对较少。
为了研究这类具有不规则几何边界的研究模型与复合缺陷相互作用下的动力学问题,Green函数的建立至关重要。在边界条件和初始条件给定的前提下,由点源入射作用而产生的位移场的基本解定义为Green函数。本文采取的模型为椭圆形孔洞,采用复变函数法中的保角映射方法将不规则边界映射为圆形边界,再推导出点源载荷作用于弹性半空间表面的任意点时产生的位移场的基本解,即Green函数,最后研究不同参数对本研究模型的动态响应的影响规律,进一步验证其精确性。
1 问题模型
图1为包含椭圆孔洞的弹性半空间模型,出平面线源载荷作用于水平表面上任意点。介质密度为ρ。图中坐标系XOY和X′O′Y′,具有以下关系式:
x′=x,y′=y+h
(1)
2 控制方程
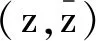
(2)

(3)

图2 椭圆外域的保角变换Fig.2 Conformal mapping of ellipse
z=ω(η)=R(η+m/η)
(4)
式中:η=Reiθ;R=(a+b)/2;m=(a-b)/(a+b),可将Z平面上椭圆边界的外域,映射为η平面上的圆形边界。
则运动方程(2)便转化为
(5)

则式(3)变成
(6)
本问题模型的边界条件如下:
(7)
3 Green函数的导出
出平面线源荷载δ(z-z0)在弹性半空间表面上任意点作用时,如图1所示,半空间内所产生的波场可记为G(i),并看作入射波,再引入映射函数z=ω(η),则其表达式可写成
(8)
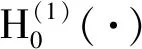
由于椭圆孔的存在而激发的散射波场记为G(s),不仅在水平自由界面上应力自由,而且满足无穷远的Sommerfeld辐射条件和运动方程(5),表达式如下:
(9)
至此,总波场的表达式如下:
G=G(i)+G(s)
(10)
相应的总应力为:
(11)
(12)
将相关的应力表达式代入边界条件(7)的第1项,可得到
(13)
式中:
在方程(13)的两侧同乘e-imθ,并在(-π,π)上积分,得到
(14)
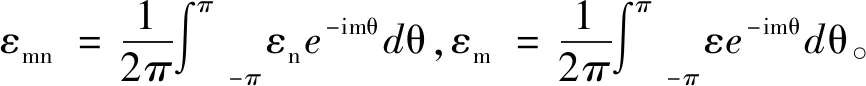
4 动应力集中系数(DSCF)
本文的主要研究内容是基于所确定的Green函数,研究出平面线源荷载作用下椭圆孔洞周围的动应力分布规律,并验证本文导出的Green函数的准确性。
(15)
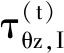
5 算例分析
基于前文的理论推导,本节通过一些具体的计算实例,给出椭圆孔周围的动应力集中系数的数据结果,从波数k1a、椭圆孔中心到水平界面距离与椭圆孔的半长轴的比值h/a、出平面荷载作用位置x1对椭圆孔外周围DSCF分布的影响规律。DSCF的表达式由式(15)定义。

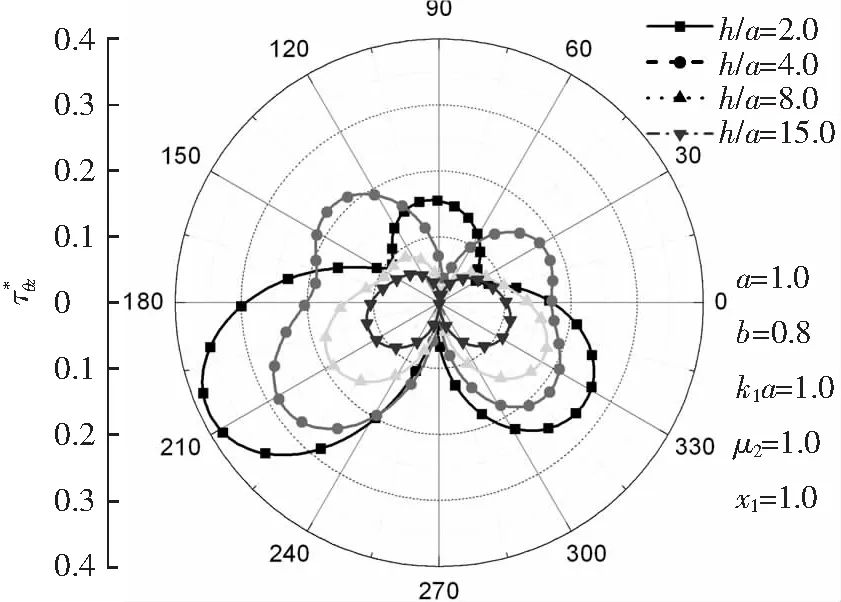
图3 椭圆孔周围的DSCF随h/a的变化Fig.3 DSCF around the elliptical cavity with h/a


图4 椭圆孔周围的DSCF随k1a的变化Fig.4 DSCF around the elliptical cavity with k1a


图5 椭圆孔周围的DSCF随x1的变化Fig.5 DSCF around the elliptical cavity with x1

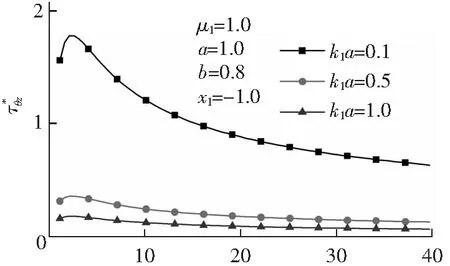
h/a图6 θ=0°处DSCF随h/a的变化Fig.6 Variation of DSCF at θ=0°with h/a
6 结论
(1) 椭圆孔圆心与水平自由界面的距离、出平面线源荷载的作用位置、入射波数等因素对椭圆孔外周边的动态响应有很大的影响。
(2) 进一步利用本论文的Green函数解,可以解决半空间或全空间中椭圆孔或夹杂和裂纹缺陷相互作用下的动态响应问题,并将其拓展至更复杂的问题模型的研究中,如探索多个椭圆孔洞或夹杂与裂纹缺陷的模型,可为地下复杂构造和复杂裂纹缺陷的勘探及无损检测等领域提供理论参考。
