碳酸盐岩三重介质气藏NPI产量递减分析研究

付天宇，刘启国，岑雪芳，李隆新，彭 先

（1.西南石油大学石油与天然气工程学院，四川成都610500；2.宁波华润兴光燃气有限公司，浙江宁波315000；3.中国石油西南油气田公司勘探开发研究院，四川成都610041）

NPI 产量递减分析最早是由BLASINGAME 提出的[1]，这一方法是基于边界控制流基础上，以压力积分及其导数和物质平衡拟时间的函数关系建立典型分析曲线，并与产量规整化处理的实际数据进行拟合分析。相比传统产量递减分析图版，所得图版不仅可以反映出受边界影响的拟稳定流动阶段特征，还可以反映出早期不稳定流动阶段特征。这种方法的优点在于经过积分处理消除了数据分散带来的影响[2]，降低了对数据的精度要求，扩大了可使用数据的范围，使得不稳定流动阶段的数据也可被用来分析，降低了分析结果的多解性。CLARKSON 等[3]针对页岩气藏的复杂情况，在双重介质基础上进行了NPI方法分析，进一步证明了NPI方法的优越性。刘晓华等[4]针对现代产量递减分析方法理论进行了详细的论述,并进行了实例分析测算。孙召勃[5]利用点源函数法求解出均质和双重介质顶底封闭、侧面封闭油藏水平井和压裂水平井的定产压力解，绘制出NPI方法复合图版并做出敏感性分析。祝晓林等[6]针对海上均质矩形边界油藏，考虑了表皮系数的影响，建立了NPI理论图版，对油气井的渗流特征及原始地质储量预测作用显著。肖翠[7]根据煤层气的等温吸附性基质收缩效应，引入Palmer-Mansoori 双重介质模型，对物质平衡拟时间进行了修正，利用NPI方法进行分析，所得结果与数值模拟基本一致。刘宝华等[8]利用安达凹陷6 口双重介质试采井生产数据进行了NPI等方法的现代产量递减分析，对地层动态参数进行了拟合分析，证实其较好的适用性。崔彬等[9]系统阐述了现代产量递减分析方法的发展，并应用NPI等现代产量递减分析方法对某煤层气井组生产数据进行了实例分析。

碳酸盐岩储层在溶蚀或破裂作用下，会产生大量的溶蚀孔洞[10]，进一步复杂化孔隙介质。针对碳酸盐岩储层中复杂的孔隙介质系统，CLOSSMAN[11]提出了三重孔隙介质模型，而后学者们在此基础上不断创新[12-18]，建立了多种三重介质模型，并进行了试井分析求解。但是针对三重介质的现代产量递减分析的研究，还存在不足，尤其是NPI 产量递减分析的研究，更是鲜有文章提到。

针对碳酸盐岩气藏建立了三孔单渗并行窜流模型，通过拉普拉斯变换对模型进行求解，并且用压力积分的方法绘制了NPI方法复合图版，对图版进行了敏感性分析。所得图版能够通过拟合方法计算出储层参数和气井控制储量，并对井的生产特征进行诊断，具有较好的应用价值。

1 物理模型建立

该模型中基质、裂缝与溶洞共同存在且视为连续介质系统，裂缝作为渗流通道向井筒提供流体，基质和溶洞作为储集空间分别向裂缝窜流[19]，如图1所示。

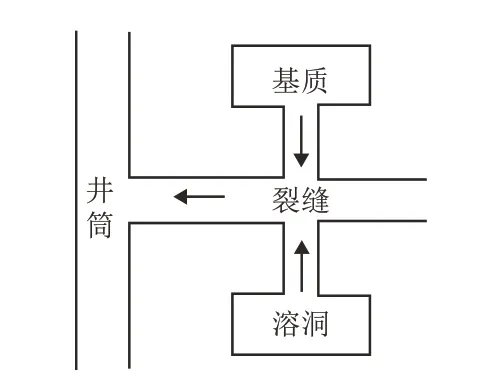
图1 碳酸盐岩气藏三孔单渗并行窜流模型Fig.1 Triporate-uniphase parallel inter-porosity flow model

对模型作出以下假设：

1）圆形封闭气藏均匀且各向同性；

2）垂直气井位于地层正中心；

3）地层中流体为单相可压缩气体，渗流符合达西定律；地层岩石微可压缩，压缩系数为常数；

4）考虑表皮效应的影响，不考虑重力和毛管力的影响；

5）各点初始地层压力均等于原始地层压力；

6）3种介质的物性参数不相互影响。

2 数学模型求解

根据质量守恒原理，引入AL-HUSSAINY[20]定义的拟压力将非线性的流动方程线性化，可得无因次渗流数学模型：

其中：

对式（1）进行Laplace 变换，可以得到拉氏空间下的无因次渗流数学模型，消去基质拟压力变量与溶洞拟压力变量化简得：

其中：

式（2）的通解为：

将通解式（4）代入式（2）中的内、外边界条件，联立方程可求得通解系数A与B：

则无因次数学模型的解即为：

当rD=1，得到上述模型无因次井底拟压力解即为：

结合Duhamel原理，可得到考虑表皮系数的无因次井底拟压力解：

可以表示为：

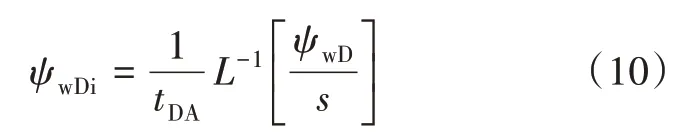
其微分形式为：

定义拟压力积分导数为：

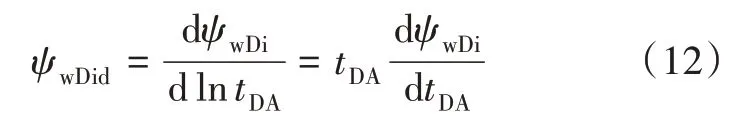
将式（11）代入式（12），可进一步表示为：

以上就求得了无因次拟压力、无因次拟压力积分和无因次拟压力积分导数[21]。

3 三孔单渗并行窜流模型NPI 方法复合图版

通过Stehfest 数值反演求得无因次井底拟压力实空间解，通过积分处理得到无因次拟压力积分与无因次拟压力积分导数。取参数ωf=0.01，ωv=0.1，λvf=10-4，λmf=10-6，RD=104，S=0 绘制出三孔单渗并行窜流模型NPI 方法复合图版如图2 所示。红色曲线为无因次拟压力曲线，蓝色曲线为无因次拟压力积分曲线，绿色曲线为无因次拟压力积分导数曲线。曲线较好地表现出了2个窜流阶段，在晚期拟稳定流动阶段无因次拟压力积分与无因次拟压力积分导数曲线为斜率为1的直线。

图2 三孔单渗并行窜流模型NPI方法复合图版曲线Fig.2 NPI method curves of triporate-uniphase parallel inter-porosity flow model

对流动阶段进行了划分。

第1段为纯裂缝流动阶段，该阶段无因次拟压力积分导数为0.5 的水平线；第2 段为溶洞向裂缝窜流过渡段，随着流体产出，窜流系数较大的溶洞系统最先向裂缝窜流，无因次拟压力导数曲线出现凹子状特征；第3 段是溶洞与裂缝系统的径向流动阶段，该阶段的无因次拟压力积分导数为0.5 的水平线；第4段为基质向裂缝窜流过渡段，无因次拟压力积分导数出现凹子状特征；第5 段为总系统的径向流动阶段，该段描述了整个系统的径向流动，无因次拟压力积分导数为0.5 的水平线；第6 段为边界控制拟稳定流动段，在该流动阶段无因次拟压力积分及其导数曲线逐渐重合为斜率为1的直线。

由上述计算结果可知，降深因素无论对排水量还是剩余水头高度都有较大的影响，且基本呈正比例关系。其中排水量与降深的比例系数为0.802～0.955，剩余水头与降深的比例系数为0.146～0.389。故从降深的角度来看排水量与剩余水头高度的计算结果，降深越小越好。

4 NPI方法复合图版敏感性分析

由模型的解可知，三孔单渗并行窜流模型NPI方法复合图版受窜流系数、储容比和供给半径等参数的影响，敏感性分析过程中其余参数同第三节。

1）裂缝弹性储容比的影响

图3 反映了裂缝弹性储容比对NPI 方法复合曲线的影响。裂缝弹性储容比主要影响无因次拟压力积分导数曲线溶洞向裂缝窜流的“凹子”特征；裂缝弹性储容比越小，说明溶洞发育越好，裂缝发育越差，溶洞向裂缝的窜流需要更长的时间，无因次拟压力积分导数曲线上溶洞向裂缝窜流的“凹子”越深，持续时间越长。

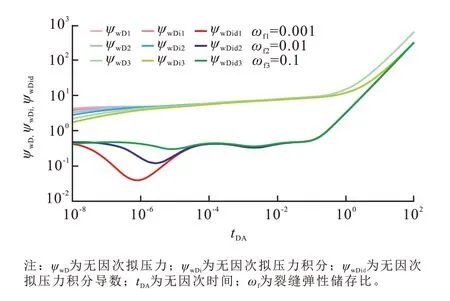
图3 裂缝弹性储容比对NPI方法复合图版的影响Fig.3 Impact of fracture storage ratio on NPI method curves

2）溶洞弹性储容比对曲线的影响

图4 反映了溶洞弹性储容比对NPI 方法复合曲线的影响。溶洞弹性储容比对两个窜流阶段的无因次拟压力积分导数曲线均有较明显的影响。在三重介质系统中，3种介质弹性储容比之和为1。因此，当裂缝弹性储容比不变时，溶洞弹性储容比和基质弹性储容比的变化是相对的；针对溶洞向裂缝的窜流，溶洞弹性储容比越小，相当于裂缝的弹性储容比越大、裂缝越发育，无因次拟压力积分导数曲线上溶洞向裂缝窜流的“凹子”越浅且持续时间越短；针对基质向裂缝的窜流，溶洞弹性储容比越小，相当于裂缝的弹性储容比越小、裂缝越不发育，无因次拟压力积分导数曲线上基质向裂缝窜流的“凹子”越深且持续时间越长。

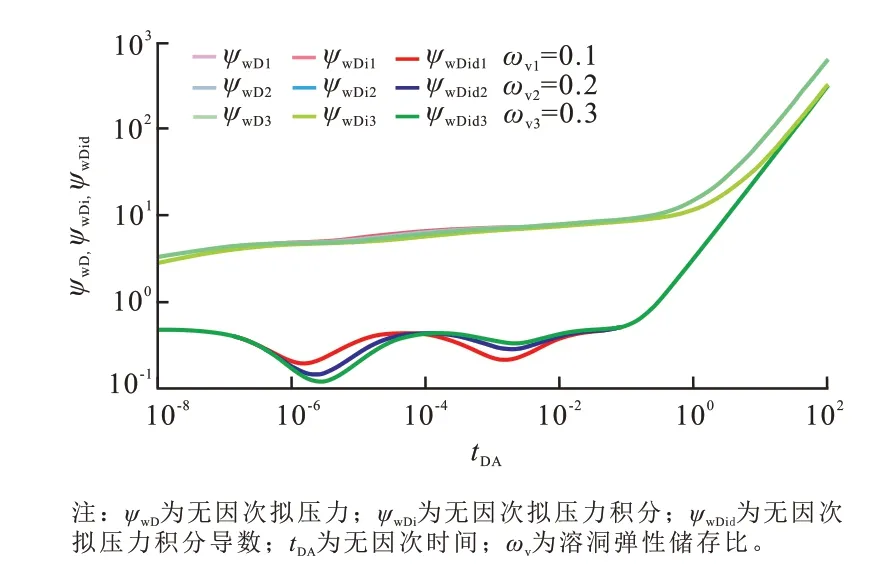
图4 溶洞弹性储容比对NPI方法复合图版的影响Fig.4 Impact of cave storage ratio on NPI method curves

3）溶洞向裂缝窜流系数的影响

图5 反映了溶洞向裂缝窜流系数对NPI 方法复合曲线的影响。溶洞向裂缝窜流系数越大，表明溶洞与裂缝的渗透率差异就越小。裂缝密度就越大，则窜流发生的时间就越早，无因次拟压力积分导数曲线上的溶洞向裂缝窜流的“凹子”就越往左平移。

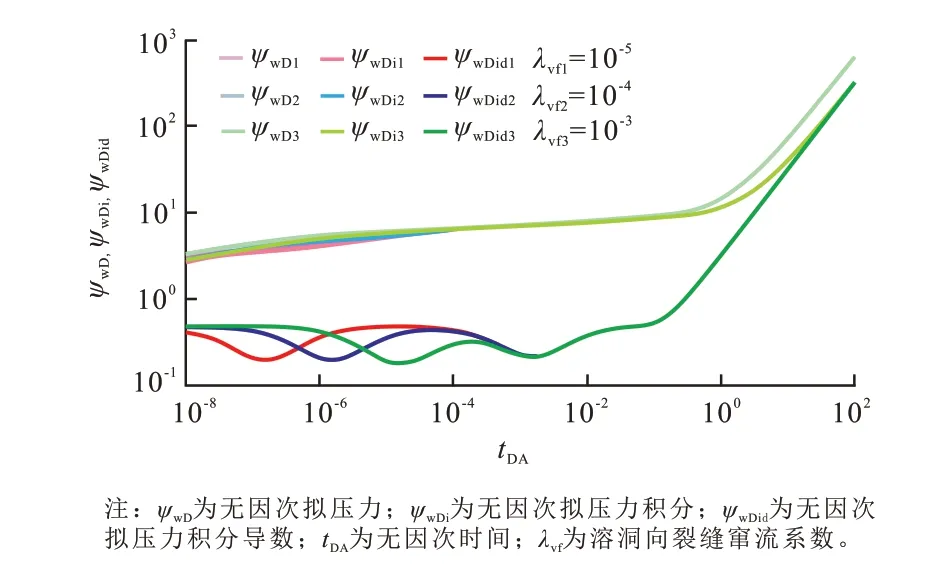
图5 溶洞向裂缝的窜流系数对NPI方法复合图版的影响Fig.5 Impact of inter-porosity flow coefficient between cave and fracture on NPI method curves

4）基质向裂缝窜流系数的影响

图6 反映了基质向裂缝窜流系数对NPI 方法复合曲线的影响。基质向裂缝窜流系数越小，表明基质与裂缝的渗透率差异就越大或者裂缝密度就越小，则窜流发生的时间就越晚，无因次拟压力积分导数的基质向裂缝窜流的“凹子”的位置就越往右平移。

图6 基质向裂缝窜流系数对NPI方法复合图版的影响Fig.6 Impact of inter-porosity flow coefficient between matrix and fracture on NPI method curves

5）供给半径的影响

图7 反映了供给半径对NPI 方法复合曲线的影响。供给半径的大小只会影响不稳定流动阶段，而不会影响晚期拟稳定流动阶段的特征。供给半径越小，总系统径向流阶段持续时间越短，总系统径向流特征越不明显，基质向裂缝的窜流将发生在边界控制阶段以后。由于无因次时间tDA按井控制面积定义，供给半径越大，相同时间对应的tDA越小，因而在无因次拟压力积分导数曲线上，2个窜流段的“凹子”将越靠左。

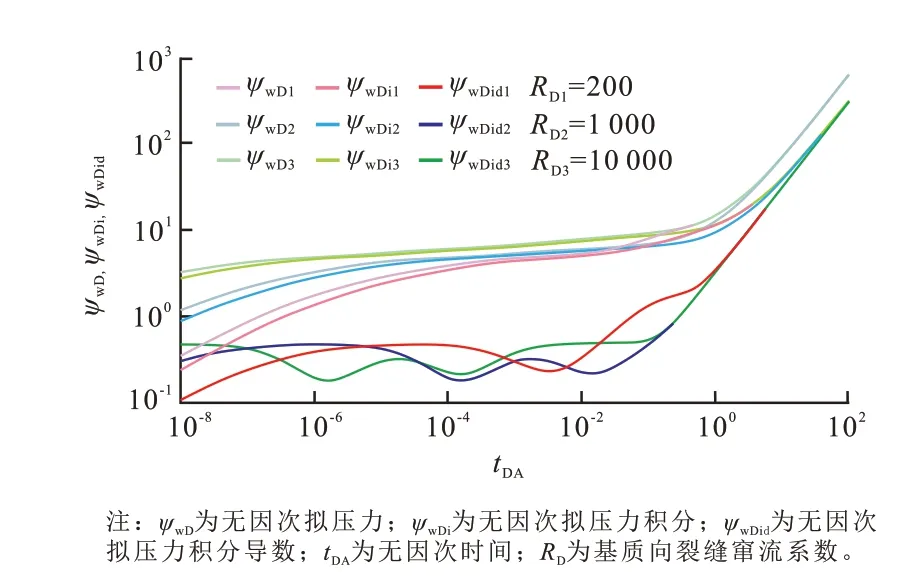
图7 供给半径对NPI方法复合图版的影响Fig.7 Impact of dimensionless outer boundary radius on NPI method curves

5 实例分析

某碳酸盐岩气井基本参数如下：原始地层压力为52.8 MPa，温度为123.97 ℃，井筒半径为0.1 m，储层厚度为408.3 m，孔隙度为5.17%。采用该文研究模型进行拟合解释，对实际生产数据进行产量规整化处理，拟合解释结果如表1 所示，拟合效果如图8所示，拟压力积分曲线拟合效果较好；由于早期实际数据点间距较大，且窜流过程持续时间较短，因此拟压力积分导数曲线早期段拟合效果稍差，但晚期段拟合效果较好。其中拟压力积分Pearson 相关系数为0.998，拟压力积分导数Pearson 相关系数为0.558，拟压力积分导数晚期段Pearson相关系数为0.713。

图8 NPI拟合曲线Fig.8 NPI production decline fitting-curves

表1 拟合解释结果Table 1 Fitting interpretation results

产量规整化处理方法如下：

6 结论

1）建立并求解了圆形封闭边界条件下，溶洞与基质为储集空间、裂缝为流动通道的碳酸盐岩气藏三孔单渗并行窜流递减分析模型。

2）通过Stehfest 数值反演法绘制出了NPI 方法复合图版，溶洞和基质向裂缝的窜流在拟压力积分导数曲线上呈现明显的“凹子”特征，不同供给半径对应的拟压力积分导数曲线在晚期拟稳定流动阶段重合为斜率为1的直线。

3）裂缝弹性储容比越小，溶洞向裂缝窜流凹子越深越宽；溶洞弹性储容比越小，溶洞向裂缝窜流凹子越浅越窄，基质向裂缝窜流凹子越深越宽。窜流系数越大，窜流发生越早，对应窜流段凹子越往左移。供给半径越大，两个窜流段的“凹子”将越靠左。

符号说明

ψmD为无因次基质系统拟压力；ψfD为无因次裂缝系统拟压力；ψvD为溶洞系统拟压力；rD为无因次半径；λvf为溶洞向裂缝窜流系数；λmf为基质向裂缝窜流系数；ωm为基质弹性储容比；ωf为裂缝弹性储容比；ωv为溶洞弹性储容比；tDA为无因次时间；RD为无因次供给半径；A 为常数；B 为常数；I0为第Ⅰ类零阶虚宗量Bessel函数；K0为第Ⅱ类零阶虚宗量Bessel函数；I1为第Ⅰ类一阶虚宗量Bessel 函数；K1为第Ⅱ类一阶虚宗量Bessel 函数；Km为基质渗透率，10-3μm2；Kf为裂缝渗透率，10-3μm2；Kv为溶洞渗透率，10-3μm2；αvf为溶洞向裂缝窜流过程形状因子，1/m2；αmf为基质向裂缝窜流过程形状因子，1/m2；h为储层厚度，m；q为产量，104m3/d；T为温度，K；φf为裂缝孔隙度；φm为基质孔隙度；φv为溶洞孔隙度；Ctf为裂缝压缩系数，1/MPa；Ctm为基质压缩系数，1/MPa；Ctv为溶洞压缩系数，1/MPa；t为时间，h；μ为黏度，mPa·s；s为拉普拉斯变量；S为表皮系数；rw为井筒半径，m；ψwD为无因次井底拟压力；ψwDi为无因次井底拟压力积分；ψwDid为无因次井底拟压力积分导数；tc为物质平衡时间，h。