考虑粘结面厚度的局部粘结单元法

盛泽强， 王毓杰， 张振南

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

1 引 言

脆性材料断裂模拟一直深受关注，目前大部分模拟方法依赖于经典连续介质断裂力学理论，但其具有一定局限性。材料发生断裂破坏，由连续介质转变成非连续介质，原本构关系不再适用；传统断裂理论在断裂模拟时需要考虑外部断裂准则和网格重划分等棘手问题。粘结单元法[1]CFEM(Cohesive finite element method)为解决这些问题提供了一种有效方法。该方法在连续介质单元边界上插入界面单元，引入蕴含材料断裂和强度准则的粘结法则(Cohesive law)来描述界面行为裂纹沿界面单元扩展，避免了断裂准则选取与网格重构问题。粘结法得到了国内外学者的广泛关注和应用，如利用CFEM研究断裂能随着裂纹速度增加与裂纹分叉引起的比表面积增加之间的关系[2]及脆性材料裂缝扩展模拟等[3]。因为该方法考虑了界面特性，所以也用于模拟分层复合材料的裂纹起裂和扩展[4,5]。

虽然CFEM在模拟脆性材料断裂方面表现出很大的优势，但仍存在一些不足，主要表现在随着粘结单元(Cohesive interface)的数量增加，宏观刚度折减，这种刚度折减受制于粘结单元尺寸和粘结刚度[6]。Tomar等[7]建议采用单元尺寸的上下界限来平衡刚度折减和准确性关系。也有学者通过提高粘结单元和体单元的刚度比来缓解刚度折减问题[8,9]。为了减弱全域范围插入粘结单元造成的刚度折减和计算效率降低的问题，Camacho 等[10]提出了局部CFEM。规定只有应力达到材料强度时才在该应力区插入界面单元。这种方法使得刚度折减问题得到了解决，但同时也带来了局部网格重划分和结点重叠等一系列问题。Zhang等[6]提出了约束粘结单元法CFEM(constrained)，当粘结面状态满足特定条件时激活粘结单元，提高了计算效率，也缓解了刚度折减问题。

粘结单元法数值计算收敛问题主要由两方面造成。(1) 隐式算法中无厚度的粘结单元容易在软化行为中造成能量释放问题，引起局部不稳定[11]；(2) 粘结单元设置过大的罚刚度引起的数值振荡[12]。有学者在粘结法则中引入粘性系数以消散材料软化阶段的能量释放[11,13]，但这类方法涉及额外起裂准则和粘性系数的选取，增加了计算成本。Sarrado等[14]提出了将无厚度粘结面嵌入线弹性基质单元的方法，将材料的弹性模量和粘结面的初始罚刚度解耦，从而解决了罚刚度过大引起的收敛性问题。Manzoli等[15]将粘结面考虑成实体单元，即在体单元间插入由两个大长宽比HAR(High-aspect-ratio)的三角单元组成的粘结单元对，通过损伤变量反映HAR单元的退化。HAR单元采用与体单元相同的强度，不需要单独考虑粘结面的罚刚度，避免过大的初始罚刚度引起的收敛性问题。该方法应用于准脆性材料的断裂[15]和水力压裂问题的模拟[16,17]，然而只考虑了HAR单元法向变形的影响，对粘结面交叉点的空白处未作处理，因此仍有待完善。

在已有研究基础上，本文提出了考虑厚度的局部粘结单元法TCFEM(Cohesive Finite Element Method with Thickness)。TCFEM在潜在裂纹扩展区内插入粘结单元，将无厚度的粘结单元转换成大长宽比的四边形实体单元，采用拓展虚内键(AVIB)本构[18]。当粘结单元完全开裂后，将自动转变成只有抗压刚度的Goodman节理单元。同时，将粘结面交叉处的空穴作为一个离散虚内键(DVIB)模型[19]的多边形键元胞来处理。相较于已有的考虑厚度的粘结面方法，TCFEM模型不需要单独考虑粘结面的初始强度和损伤变量，且虚内键模型考虑了法向和切向变形的贡献，模型的几何完整性也得到了完善。

2 TCFEM建模

TCFEM模型由体单元、考虑厚度的粘结单元和多边形键元胞组成(图1)。体单元在加载卸载中始终遵循线弹性本构关系；而材料的非线性行为由粘结单元和多边形键元胞承担。考虑厚度的粘结单元采用AVIB本构[18]，多边形键元胞满足DVIB模型[19]。

图1 TCFEM的单元组成

2.1 考虑厚度的粘结单元本构关系

AVIB源于虚内键(VIB)，VIB是Gao等[20]提出的一种固体宏微观本构模型。由于虚内键势函数蕴含了微观断裂机理，因此在模拟断裂问题时不需要额外的断裂准则。AVIB通过引入Xu-Needleman势函数表征颗粒间法向及切向相互作用，克服了原VIB模型固定泊松比限制。AVIB考虑了脆性材料拉压强度差异，适合准脆性材料的断裂模拟。

根据文献[18]，虚内键的Xu-Needleman势函数描述为

(1)

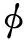
(2)

式中l0为虚内键的原长，ε为应变张量，ξ为变形前虚内键的方向向量，上标T表示转置。对于体积为V的代表单元体，其应变能密度为

(3)

根据超弹理论，应力张量和切线模量张量可表示为

(4)

在平面应力情况中，微观虚内键参数与宏观材料常数之间关系为

(5)

式中E为杨氏模量，ν为泊松比。

为了避免AVIB在应变软化的单元尺寸敏感性问题，Zhang等[18]提出在不改变材料强度条件下调整材料参数的方法，即软化后的材料弹性模量和应变强度为

(6)

(7)

式中J为材料临界J积分，h为粘结单元的厚度。

按式(6)调整材料参数主要是保证软化过程中材料断裂能守恒。对于裂尖单元不能一开始就应用调整后的材料参数，而应该是在进入峰后软化阶段才调整。在进入软化阶段前，材料还是由原来的材料参数控制。因此，裂尖材料开始调整参数的条件可表示为

(8)

当有厚度粘结单元的应变超过一定值时就意味着裂纹生成，此时粘结单元将自动转化为接触单元，以反映裂纹面之间的接触和摩擦。粘结单元转化为接触单元的条件可表示为

(9)

式中λ为大于1的系数。考虑计算效率问题，隐式计算的时间步长不能取得过小。在此情况下，如果λ取值刚好大于1，则在一个时间步内，裂尖会有很多粘结单元应变满足式(9)，而这些粘结单元并非真的已发生断裂；如果λ取值太大，则会出现已发生断裂的粘结单元没有识别出来；同时也考虑到粘结面峰后能量释放问题，本文取经验值λ≈3.0。

式(9)实际上为裂纹识别准则，其与一般材料破坏准则(如王来贵等[21])不同。本文采用AVIB本构，单元是否破坏由AVIB本构来控制。式(9)是将已断裂的粘结单元识别出来。

2.2 粘结面交叉多边形空穴本构关系

在体单元边界插入有厚度的粘结单元后，在粘结面交叉点会形成不规则的多边形空穴，如图2所示。这些空穴的存在使得计算模型与原完整模型不匹配，人为地在原材料中引入了缺陷，空穴周围引起应力集中，削弱了原材料的强度。为了弥补这一模型缺陷，本文将此多边形空穴当作一个键元胞补上，采用DVIB[19]方法对其进行描述，即键元胞的节点力向量F为

(10)

键元胞的刚度矩阵Κ为

(11)

式中ui为键元胞中结点的位移向量。

键元胞中的键能参数与宏观材料常数的关系为

图2 粘结面交叉点处的多边形键元胞

(12)

式中Ω为键元胞的虚内键数量。

考虑到裂纹只能沿着粘结单元发生，粘结单元端点间通过多边形键元胞衔接，故也需要引入键元胞破坏准则。为了简化处理，认为结点键元胞为弹脆性。因而可采用键的应变准则来判断键是否发生断裂，即

(13)

当键元胞的虚内键断裂总量达到一定值时[19]，可认为键元胞发生破裂。

3 数值实现

3.1 TCFEM网格生成算法

本文开发了在指定区域内生成有厚度粘结单元的算法。如图3(a)所示，在常规网格的红圈范围内生成无厚度的粘结单元，将这些单元按比例缩小，从而在单元之间形成了一定厚度间隙，如图3(b)所示。在单元之间插入有厚度粘结单元，对于粘结面交叉处形成的空穴区域，引入多边形键元胞进行填充，最终形成一个完整的网格结构，如图3(c)所示。

图3 生成有厚度粘结单元的主要步骤

3.2 数值实现过程

在数值模拟过程中采用隐式算法，通过Newton-Raphson法进行迭代计算。在计算过程中分别得到体单元、粘结单元和多边形键元胞的刚度矩阵，整合成总体刚度矩阵，采用有限元方法进行处理和求解，具体计算流程如图4所示。

图4 TCFEM模型计算流程

4 数值模拟与验证

4.1 考虑厚度的粘结单元长宽比影响

本文引入的粘结单元对比常规四边形单元具有很大的长宽比，达到了1∶10及以上。漆文邦[22]指出，四边形单元的计算精度会随着长宽比的增大而降低。本文的粘结单元主要是为了表现体单元间的粘结作用，以抗拉特性为主，因此只需保证粘结单元的应变计算精度在可接受范围内即可。

为了验证单元长宽比对模型精度的影响，采用图5(a)的悬臂梁进行模拟。梁长L=8 m，高D=1 m，悬臂端承受分布剪力P=1 kN。材料参数为E=30.0×109Pa，v=0.25，梁的厚度为一个单元长度。按照平面应变问题求解。模拟悬臂梁的单元网格如图5(b)所示，在网格中间层插入单层粘结单元，自由端承受分布剪力。

该梁自由端中间点挠度的解析解[22]为

(14)

粘结单元的长宽比分别取10∶1，20∶1和 50∶1，将模型计算结果与解析解对比，误差分别为 1.0853%，1.1131%和1.1340%。表明单元长宽比越大，引起的误差也越大，与文献[22]结论一致。但模拟结果误差都在可接受范围内，因此单元的长宽比不是影响本方法准确性的重要因素。考虑到单元过大的长宽比会影响收敛性，故本文模拟算例中，粘结单元长宽比的取值均为10∶1。

图5 粘结单元长宽比对计算精度的影响算例

4.2 算例验证

4.2.1 拉伸型裂纹扩展模拟

图6 三点弯(TPB)实验试件尺寸(D =75 mm)与加载方案

图8为三点弯梁的网格图，在试件槽口附近潜在的裂纹扩展路径区域插入有厚度的粘结单元(图8 详图)。粘结单元的具体厚度根据单元尺寸决定，约为单元边长的1/10。同时为了验证网格尺寸是否对模拟结果有影响，采用了两种尺寸的网格，即粗网格(单元总数为7369，结点总数为3828(size1))和细网格(单元总数为13126，结点总数为6742(size2))。

图7 通过AVIB本构模拟的单轴拉伸应力-应变曲线

图8 三点弯梁(TPB)实验试件网格及局部网格详图

模拟结果如图9所示。与文献[23,24]相比，模拟的力位移曲线(图9(a))与实验结果吻合较好；同时,试件的变形和裂纹扩展路径也与试验基本一致(图9(b))，说明该方法可以模拟材料拉伸断裂行为。而且粗细网格模拟的结果也基本一致，说明模拟过程中断裂能是守恒的，在很大程度上消除了单元尺寸敏感性问题。图9(a)中曲线的峰值存在微小下降，主要是因为插入粘结单元后材料会发生一定程度的软化。与传统CFEM相比，由于本文方法采用有厚度粘结单元，相当于实体单元，因而不存在刚度折减问题。

4.2.2 复合型裂纹扩展模拟

图9 三点弯梁(TPB)试验与模拟结果

图10 复合型试验试件尺寸与加载方案

梁变形如图11(b)所示。

图11 复合型裂纹试验结果(方案1)

图12为第二种加载方式下的两种试件模拟结果。图12(a)显示，P -CMOD 曲线的模拟结果与实验结果基本吻合。试件加载中，裂缝从预设裂缝尖端起裂并发生扩展。图12(b)显示裂纹扩展路径向加载点位置偏转延伸，与实验结果基本一致。这说明TCFEM方法可以有效再现复合型裂纹扩展行为。

图12 复合型裂纹试验结果(方案2)

5 结 论

本文发展了一种考虑厚度的局部粘结单元法，用于脆性材料的断裂模拟。数值实现过程中，将指定区域内的体单元按比例缩小，使单元之间形成一定间隙，从而生成有厚度的粘结单元。采用AVIB本构模拟粘结单元。由于粘结单元有了厚度，在粘结面交叉处形成多边形空穴，采用DVIB键元胞将其补上，以保持计算模型的几何完整性。由于插入的粘结单元是有厚度的实体单元，在软化行为前采用与体单元相同的刚度，避免了传统CFEM方法的刚度折减问题以及罚刚度过大而引起的收敛性问题。采用DVIB模型弥补了由于粘结单元厚度引起的粘结面交叉处多边形空穴问题，保证了计算模型的几何完整性。通过悬臂梁挠曲变形、混凝土梁三点弯和四点弯试验模拟及对比，表明本文方法是有效的。本方法将在准脆性材料断裂问题研究中具有广阔的应用前景。