建筑结构基于巴斯金风速谱的系列风振响应的简明封闭解

2022-01-06张梦丹葛新广

计算力学学报 2021年6期

李暾，张梦丹，姜琰，葛新广*,2

(1.广西科技大学土木建筑工程学院，柳州 545006; 2.上海交通大学船舶海洋与建筑工程学院，上海 200240)

1 引言

近年来，随着结构分析和建筑水平的不断提高，建筑结构向着高、大、柔和细的方向发展，结构风振效应更加突出。根据产生机理，风对建筑结构的振动影响分为顺风向和横风向振动。脉动风是引起建筑顺风向随机振动的主要因素，横风向振动则较为复杂，根据雷诺数将风振细分为亚临界、超临界和跨临界振动，其中亚临界和跨临界振动为确定性周期振动，而超临界振动则具有随机性，相对于顺风向振动影响较小[1-4]。风工程领域研究风对结构的影响主要有风洞试验[5,6]和理论分析[7-14]，风洞试验能准确考虑风场与建筑的相互作用，根据相似性准则制作不同的缩尺模型，通过刚体测压试验获得结构表面的风压体型系数，通过节段模型试验研究结构的振动响应，通过气弹模型试验研究结构整体的气动弹性特性，但试验成本较高；而理论研究则通过分析大量试验资料，利用功率谱概念来表述脉动风对结构的作用，所得结果基本能满足工程精度要求。因此，风的随机理论分析是结构风振响应分析的重要方法。工程上常采用风速谱描述脉动风的随机过程，根据风速谱的统计方法分为两类，一类是将强风记录仪通过超低频滤波器，直接获得脉动风的功率谱密度函数，Davenport谱[11]和Simiu谱[12]属于这一类，均采用分数指数形式表示，是根据强风记录，不易获得结构响应的简明封闭解[2,3,7]；另外一类是将强风记录通过相关分析，得到相关曲线，再利用Wiener-Khinchin公式获得风速谱的功率谱密度函数，而巴斯金风速谱属于此类，其采用整数指数(有理式)形式，目前仅获得偶数阶响应谱矩解[10,13]，且表达式也比较复杂，又无1阶谱矩的响应解，无法用于基于首超破坏准则及Vanmark假设的动力可靠度分析[15,16]。

本文针对巴金斯谱激励下结构的风振响应分析解析解表达式复杂或者需要数值积分的问题，提出了一种分析结构风振响应0～2阶谱矩及4阶谱矩的简明封闭解法。首先，基于留数定律[17]提出了巴斯金谱的二次正交式；其次，利用复模态方法[7，18]和虚拟激励法[19]提出了结构系列响应(结构层绝对位移及其振动速度、层间位移及其变化率)的频响函数的二次正交式，进而获得结构系列响应功率谱密度函数的二次正交式；最后，根据随机振动理论中谱矩的定义[18]，获得结构风振系列响应的0～2阶和4阶的谱矩的简明封闭解。

2 巴金斯谱的二次正交式

建筑结构在强风作用下的振动是由脉动风压引起，脉动风压与平均风速相关并具有空间相关性，离地高度H的脉动风载pf(H,t)表示为[7,10]

pf(H,t)=I0(H)B(H)u(t)

(1)

(2)

(3)

式中μs(H)和w0分别为离地H高度处的风荷载体型系数和基本风压，A为结构风压力计算的迎风面积。

巴斯金风速谱的功率谱采用有理式[2,13],

(4)

为了便于获得简明封闭解，利用留数定理[17]获得其二次正交式，

(5)

由于脉动风对建筑结构顺风向作用具有显著的空间相关性，且竖向高度相关性最为明显，则考虑高度相关性的平稳脉动风压力的功率谱SPf(Hi,Hj,ω)[7,10]为

(6)

(7)

3 结构响应功率谱的简明解

建筑结构在横风向荷载pf(t)作用下的运动方程为

(8)

对于常规结构，风对建筑结构的作用取前m个振型，则结构的位移向量可由阵型表示为

x=φmq

(9)

式中φm为结构前m振型矩阵，为n×m矩阵；q为广义坐标向量，q=[q1…qm]T; T为矩阵转置。

把式(9)代入式(8)，并利用实模态的正交性，结构的振动方程改写为

(10)

引入状态变量：

(11)

则式(10)改写为

(12)

式中O2为m×m矩阵，其元素均为0;E1为m×m的单位对角矩阵。

根据复模态法理论[7]，式(12)存在左右特征向量V，U和特征值矩阵P使之解耦，三者存在关系，

(13)

式中特征值矩阵P为对角阵，其元素的实部为正实数。

引入复模态变换,

y=Uz

(14)

由复模态理论[7,19]，式(12)改写为

(15)

由于P为对角阵，式(15)的分量形式为

(k=1～2m)(16)

根据虚拟激励法[19]，式(16)的频域解为

(17)

由式(9，11，14)，结构响应的频域解为

(18a)

(18b)

(18c)

(18d)

从式(18)可知，结构响应的位移及速度、层间位移及其变化率可统一表示为

(19)

由虚拟激励法[19]，Dl的响应功率谱为

(20)

式(20)可获得其更为简明的表达式，

SDl(ω)=GDl(ω)Su(ω)

(21)

式中GDl(ω)为Dl的频响响应特征值函数，具体推导见附录A，其二次正交式为

(22)

由式(21)可知，建筑结构基于巴斯金风谱的动力响应功率谱可表示为结构频率响应特征值函数和巴斯金风速功率谱的代数乘积关系，具有表达式简洁的特点。由式(5,22)可知，式(21)所表示的结构响应功率谱为二次正交形式，为本文获得结构响应谱矩和方差简明封闭解奠定基础。

4 风振系列响应谱矩的简明封闭解

根据随机振动理论[19]，线性结构位移响应的0阶谱矩等于位移响应的方差；位移响应的2阶谱矩等于速度响应的0阶谱矩等于速度响应的方差；位移响应的4阶谱矩等于速度响应的2阶谱矩等于加速度响应的0阶谱矩，即加速度的方差。位移响应的方差、速度响应的方差及位移响应的0～2阶谱矩是基于Markov分布的动力可靠度分析的关键参数[15,16]。加速度方差是结构风振舒适度分析的主要参数[20,21]。为此,需要对结构位移响应的0～2阶及4阶谱矩进行分析。

根据随机振动理论，结构动力响应的谱矩为

(q=0～2)(23)

4.1 结构响应0～2阶谱矩

把式(22)代入式(23)，结构响应的q阶谱矩为

(24)

(25)

(26)

(27)

(28)

4.2 结构层绝对加速度的方差

建筑结构风振舒适度取决于结构层风振的绝对加速度[20,21]。由随机振动理论可知，结构绝对加速度的方差=绝对位移变化率的2阶谱矩。由式(18b,24)可知，结构层绝对加速度可表示为

(29)

5 算例

5.1 巴斯金风速谱的等效形式验证

图1为本文所提巴斯金谱的二次正交式与其有理式的对比，两者完全重合，验证了本文所提二次正交式的正确性。

5.2 位移功率谱对比分析

图2和图3为本文方法获得的结构响应功率谱与虚拟激励法的响应功率谱的对比。可以看出两者完全吻合，说明本文所提结构响应功率谱密度函数二次正交式的正确性。

图1 风速谱对比

图2 1层位移功率谱对比

图3 10层位移功率谱对比

5.3 谱矩分析

5.3.1 积分区间对虚拟激励法精度的影响分析

虚拟激励法的积分区间分别取[0，5] rad/s，[0，25] rad/s和[0，100] rad/s，而积分步长统一取0.01 rad/s，计算结构各层位移及层间位移的谱矩并与本文方法进行对比，如图4～图10所示。可以看出，随着积分步长的增加，虚拟激励法所得结果逼近本文方法，从而说明本文方法所得封闭解的正确性。

从图4和图8可以看出，对于0阶谱矩，虚拟激励法的积分区间取[0，5] rad/s可达到很高的精度；从图5～图7、图9和图10可以看出，对结构响应1阶和2阶谱矩及加速度方差，虚拟激励法的积分区间取[0，25] rad/s可达到很高的精度。由此可知，虚拟激励法分析不同阶谱矩时要想达到高精度，必须试算积分区间。

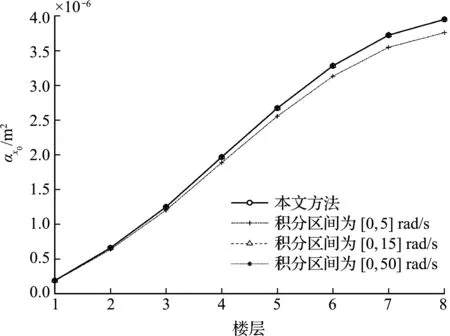
图4 位移0阶谱矩区间对比

图5 位移1阶谱矩区间对比

图6 位移2阶谱矩区间对比

图7 加速度方差区间对比

图8 层间位移0阶谱矩区间对比

图9 层间位移1阶谱矩区间对比

图10 层间位移2阶谱矩区间对比

5.3.2 积分步长对虚拟激励法的影响

根据5.3.1的分析可得，当积分区间为[0,100]时,虚拟激励法与本文方法在计算谱矩时完全吻合。为了分析虚拟激励法积分步长对其精度的影响，分别取3种积分步长，1 rad/s，0.25 rad/s和0.01 rad/s。图11～图17为不同积分步长下虚拟激励法分析谱矩与本文方法的对比。可以看出,积分步长越小，计算的谱矩与本文方法越接近，故可证明本文方法的正确性。