毛乌素沙地长柄扁桃林地土壤水分时间稳定性

赵 鑫， 朱 超， 郑云珠， 李婷婷， 于 娜， 田晓飞， 翟 胜， 孙树臣†

(1.聊城大学环境与规划学院，252059，山东聊城；2.聊城大学人力资源处，252059，山东聊城)

土壤水分是干旱、半干旱地区沙地生态系统运转的核心，推动着土壤-植被-大气连续体(SPAC系统)中物质循环和能量流动[1-2]，其动态变化影响降雨入渗、植被蒸腾、溶质运移及产流产沙等水文和生态过程[3]。受地形、海拔、土壤质地及气候等因素的影响，土壤水分在时空上具有较强的变异性[4-5]，导致某地区稳定土壤水分信息获取增加了困难。为此Vachaud团队最先发现并提出时间稳定性概念，即土壤水分的空间模式在时间上具有一定的稳定性，且某些测点在任何时间都可以较好的代表该区域的平均土壤含水量[6]。基于时间稳定性理论研究发现，空间尺度越大，环境条件越复杂，土壤水分时空变异性越强，强变异性会影响土壤水分空间模式在时间上的稳定性[7]。同一研究区表层土壤水分空间模式在时间上相似性较弱[8]，随着土层深度增加土壤水分时间稳定性逐渐增强[9]。植被在生长季会降低土壤水分时间稳定性，当土壤有效水较低且植被蒸散发受降水供给和土壤质地控制时，植被对土壤水分变异性的影响会降低[10]。另外，当研究区土壤黏粒较高、坡度较缓、地形平坦时，土壤水分具有更强的时间稳定性[11]。

毛乌素沙地位于我国西北干旱、半干旱区，降水较少，风沙活动剧烈，生态环境脆弱，土壤水分已成为该区植被恢复及生态环境改善的主要限制因子。学者们从植被[12-13]、沙丘类型[14]、地形等方面分析毛乌素沙地土壤水分动态变化并提出科学理论依据，使该地区土壤养分、水分和植被恢复有不同程度的提高。然而在人工植被建设过程中由于受自然条件和人类活动共同的影响，无论是自然生长还是人工种植的该树种均出现了枯萎死亡的现象。该区域地处干旱半干旱区，降水年际变率较大，而有关毛乌素沙地长柄扁桃与土壤水分相互作用的关系研究较少，特别是长柄扁桃大面积种植后对于该区土壤水分时空变异性及时间稳定性分析尚不清楚。因此，本研究以毛乌素沙地东南缘固定沙丘长柄扁桃(Amygdaluspedunculata)林地典型坡面为例，于2018年3月—2019年10月连续测定0～300 cm土壤含水量，分析长柄扁桃林地坡面土壤水分时空变化特征，了解各土层土壤含水量的时间稳定性差异及相关性，确定最佳代表性测点的位置，实现土壤水分有效预测，以期为该地区水资源有效利用及长柄扁桃可持续发展提供理论依据。

1 研究区概况

研究区位于毛乌素沙地东南缘陕西省神木市生态建设协会毛乌素治沙造林基地(E 109°22′、N 38°53′，海拔1 250～1 280 m)，为毛乌素沙地和黄土高原的过渡带，沙丘类型多为固定、半固定沙丘。该地区气候属于半干旱温带大陆性季风气候，四季冷暖分明，年平均温度6～9 ℃，≥10 ℃积温2 500～3 645 ℃，无霜期130～160 d；多年降水量400～450 mm，年际降水量变化较大，7—9月降水量占60%，一般多雨年是少雨年2～3倍；年均蒸发量2 100～2 600 mm，最大蒸发出现在6—8月[15]。土壤类型主要是以沙性母质发育与植被成土作用共同形成的固定风沙土为主。植被类型主要长柄扁桃、沙柳(Salixpsammophila)和紫穗槐(Amorphafrutiocosa)，以及一年生的狗尾草(Setariaviridis)等。其中长柄扁桃是该区域的先锋树种，植被覆盖率高达33%。

2 研究方法

2.1 样点布设及土壤水分测定

在毛乌素沙地东南缘选择典型固定沙丘迎风坡12 a林龄长柄扁桃林地为研究对象(植被特征见表1)，该坡面呈半弧状(坡底由西南向东北缩短)。在坡面(从左到右坡底、坡中、坡顶)建立土壤水分定位监测小区,小区规格均4 m×12 m，并设3根3 m长中子管，共30个测点(图1)。同时，将土钻采集的0～300 cm各土层的扰动土装入自封袋带回实验室，测定其土壤理化性质，利用环刀法测定0～10 cm土壤密度(表2)。小区均为长柄扁桃纯林，受海拔及微地形等影响，株高在不同坡位存在一定差异，其中坡底(# 3，# 7)生长较好。

表1 采样坡面、植被状况Tab.1 Topography and vegetation status in the sampling slope

表2 采样坡面土壤理化性质Tab.2 Soil chemical and physical properties of the sampling slope

# 1～10代表土壤水分监测小区. # 1-10 represent soil moisture measuring plots. 图1 土壤含水量测点布设图Fig.1 Layout of measuring points for soil moisture content

于2018年3月—2019年10月利用北京超能科技公司生产的中子仪(CNC503DR)进行剖面土壤水分的测定并依据校准曲线进行土壤体积含水量的计算，其中0～100 cm范围内每隔10 cm测定1次，100～300 cm范围内每隔20 cm测定1次，观测期内共测定16次。降水由雨量筒(TE525MM，Campbell, USA)监测，由数据采集器(CR1000，Campbell, USA)每0.5 h自动储存数据。

2.2 数据分析法

利用变异系数(coefficient of variation，CV)来描述土壤含水量的统计学特征在时空上的变异性[8]。利用Spearman秩相关系数测定时间下各测点土壤含水量的秩随时间变化特征[16]，其值越接近1，土壤水分空间模式在时间上越强。通过分析各测定时间下各测点土壤含水量的累积概率函数，然后判断不同时间上各测点土壤含水量的累计概率函数是否保持相同的概率。具体方法将测定时间各测点土壤含水量由小到大排列，计算每一个土壤含水量数值出现的次数占总量之间的比值，然后再累加，即可得到每个测点土壤含水量的累计概率[17]。

相对差分平均值和相对差分标准差可以判定测点土壤含水量的时间稳定性。测点i在观测时间j下的土壤含水量相对差分δij。采用平均偏差和均方根误差和R2分析代表性测点与研究区平均土壤含水量相关性。测点i的均方根误差RMSE数值越小越接近于研究区平均土壤含水量，R2越大越好。依据水量平衡原理计算长柄扁桃灌丛蒸散耗水量。

3 结果与分析

3.1 土壤含水量时空变化特征

通过2018年3月—2019年10月平均土壤含水量和变异系数在观测期动态变化可知(图2)。各土层土壤含水量随时间变化波动明显，0～50、50～100、100～200和200～300 cm土壤含水量波动范围分别为4.37%～8.07%(均值5.97%)、4.41%～8.66%(均值6.17%)、5.98%～14.15%(均值8.03%)和4.18%～36.24%(均值13.02%)，随着土层深度增加，土壤含水量逐渐增大。最小显著性差异法检验表明200～300 cm土层土壤含水量各土层差异显著(P<0.05)，其余各土层之间土壤含水量差异不显著(表3)。剖面平均土壤含水量的标准差和变异系数也存在较大差异，随着土层深度的增加标准差和变异系数逐渐增大，其值分别为0.81%、0.95%、2.10%、10.61%和13.60%、15.34%、26.34%、81.47%，变异系数均>10%，表明时间上土壤含水量具有较强的空间变异性，即各测点土壤含水量具有较大的差异。

图2 监测期内各土层平均土壤含水量季节变化Fig.2 Seasonal variation of mean soil moisture content in each soil layer during monitoring period

土壤含水量在16个测次上各土层平均值、标准差和变异系数的空间统计特征可知(表3)，各土层空间上的土壤含水量变异系数的平均值整体随着土壤深度增加而减小，0～50、50～100、100～200和200～300 cm分别为30.67%、24.18%、22.23%和20.15%，随着土层深度增加各测点土壤含水量在时间上变异性减弱。200～300 cm土层与各土层差异显著(P<0.05)，这与各土层土壤含水量差异性相似。各土层时间上平均土壤含水量的标准差在空间上的标准差和变异系数分别为0.44%和0.05%(0～50 cm)、0.37%和0.05%(50～100 cm)、1.32%和0.12%(100～200 cm)、1.34%和0.05%(200～300 cm)；各土层时间上平均土壤含水量的变异系数在空间上的标准差和变异系数分别为24.88%和17.60%(0～50 cm)、24.98%和21.24%(50～100 cm)、59.63%和46.53%(100～200 cm)、58.78%和26.31%(200～300 cm)。虽然标准差数值较低，但变异系数均>10%,土壤含水量时间上的变异系数在空间上具有较显著的变化。

表3 不同土层土壤含水量在时间上的平均值、标准差和变异系数的空间统计特征Tab.3 Spatial statistical characteristics of mean standard deviation and coefficient of variation of soil moisturecontent in different soil layers in time

3.2 土壤含水量的秩相关系数

Spearman秩相关系数可以分析研究区各测点土壤含水量空间分布的时间稳定性特征。前8次(2018年)监测期间土壤含水量秩相关系数较高(表4)，后8次(2019年)监测期间土壤含水量的秩相关系数较低，尤其在2019年5月，大部分土壤含水量秩相关系数为0.142～0.598。虽然各监测时期间土壤含水量秩相关系数波动范围较大(0.142～0.969)，但总体上各时期对之间具有极显著相关(P<0.01)。以上分析表明在2018年监测期间毛乌素沙地固定沙丘长柄扁桃林地迎风坡0～300 cm深度的土壤含水量空间分布模式在时间上稳定性较强。

表4 研究区0～300 cm不同监测时间土壤含水量的Spearman秩相关系数Tab.4 Spearman rank correlation coefficient of soil moisture content measured at different time from 0 to 300 cm in the study area

3.3 累积概率函数

累积概率函数是判断具体测点时间稳定性的有效方法，通过分析各测点土壤含水量在不同时间累积概率函数的相似性来判定时间稳定性的强弱[18]。本研究选取土壤含水量差异最大的2个时间点来代表湿润(2018年10月均值11.40%)和干旱(2019年10月均值6.79%)，比较2种极端水分条件下不同土层土壤含水量累积概率的分布特征(图3)。0～50 cm土层只有测点1保持相同的累积概率；50～100和100～200 cm土层各有3个测点保持相同的累积概率分别为11、21、24和13、6、11；200～300 cm土层测点29、28、18、6、4、5、9、11、12、10，共10个点保持相同的概率。2种极端水分条件下大部分测点的土壤含水量概率位置发生了改变，随着土层深度增加，土壤含水量空间分布的时间稳定性逐渐增强。受土层深度的影响，累积概率函数在确定研究区平均土壤含水量最佳代表点时具有一定的局限性，因此还需进一步结合相对差分平均值(mean of relative difference，MRD)和相对差分标准差(standard deviation of relative difference，SDRD)才能确定代表研究区平均土壤含水量的最佳测点。

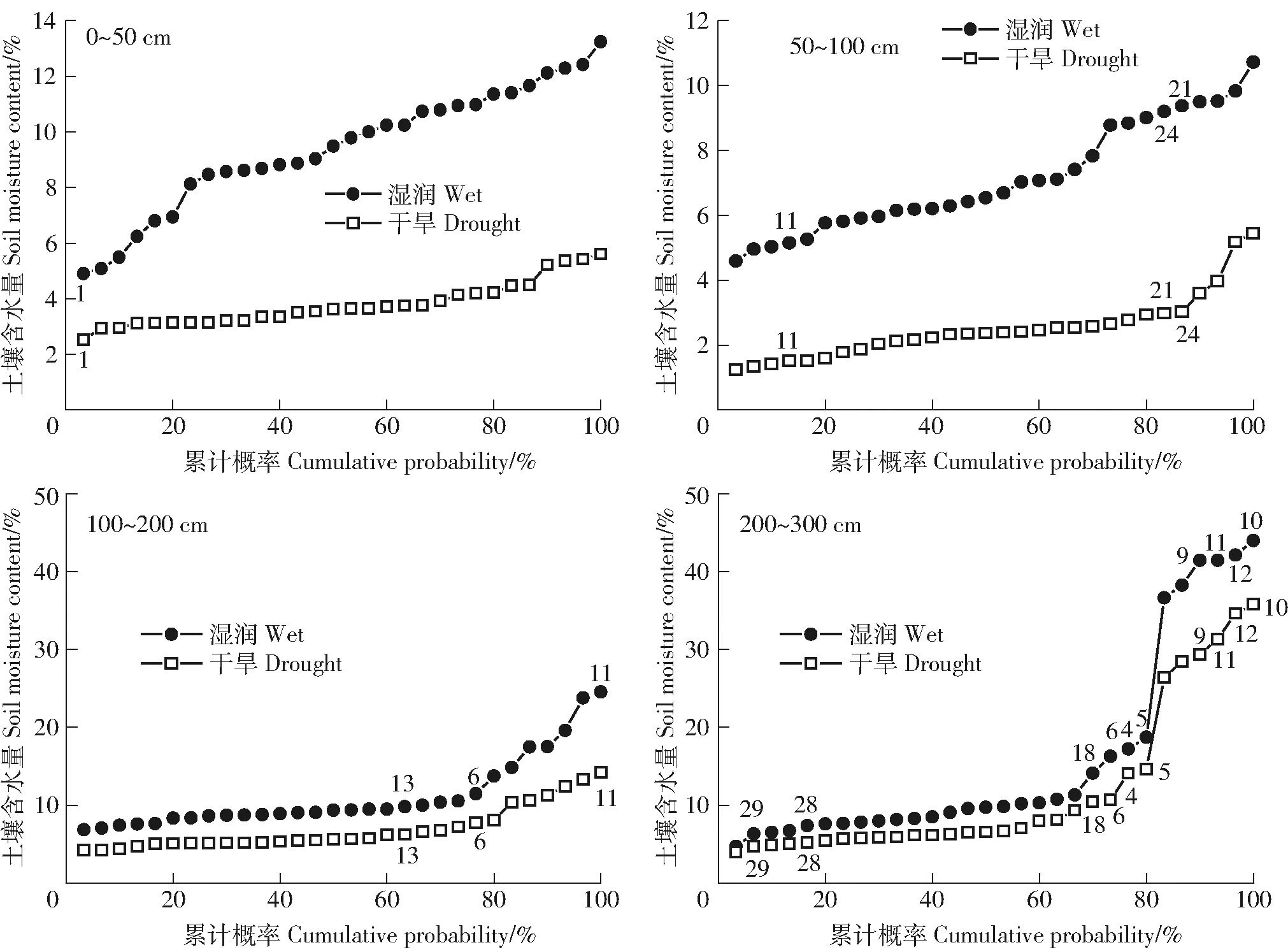
图中不同数字代表采样点，下同。Different numbers refer to sampling points，the same below. 图3 湿润和干旱条件下不同土层深度土壤含水量累积概率函数Fig.3 Cumulative probability function of soil moisture content at different soil depths under wet and dry conditions

3.4 相对差分及代表性测点的确定和合理性验证

将30个测点在0～50、50～100、100～200和200～300 cm土层土壤含水量相对差分平均值的秩数由小到大排列，垂直误差线为各测点相对差分标准差(图4)。各土层分别有15、14、10和8个测点的相对差分平均值>0，表明该研究区中大部分测点土壤含水量小于平均值。各土层土壤含水量相对差分标准差平均值分别为14.12%、9.80%、21.40%和9.52%，整体上随土层深度增加呈减小趋势。依据相对差分标准差<5%时具有较强的时空稳定性原则发现[4]，各土层相对差分标准差<5%测点数分别有0、2、0和4，结果表明大部分测点在不同深度土层具有较弱的时间稳定性，但从整体上看深层土壤含水量时间稳定性要强于浅层，土壤水分时间稳定特征对土壤深度具有较强的依懒性。

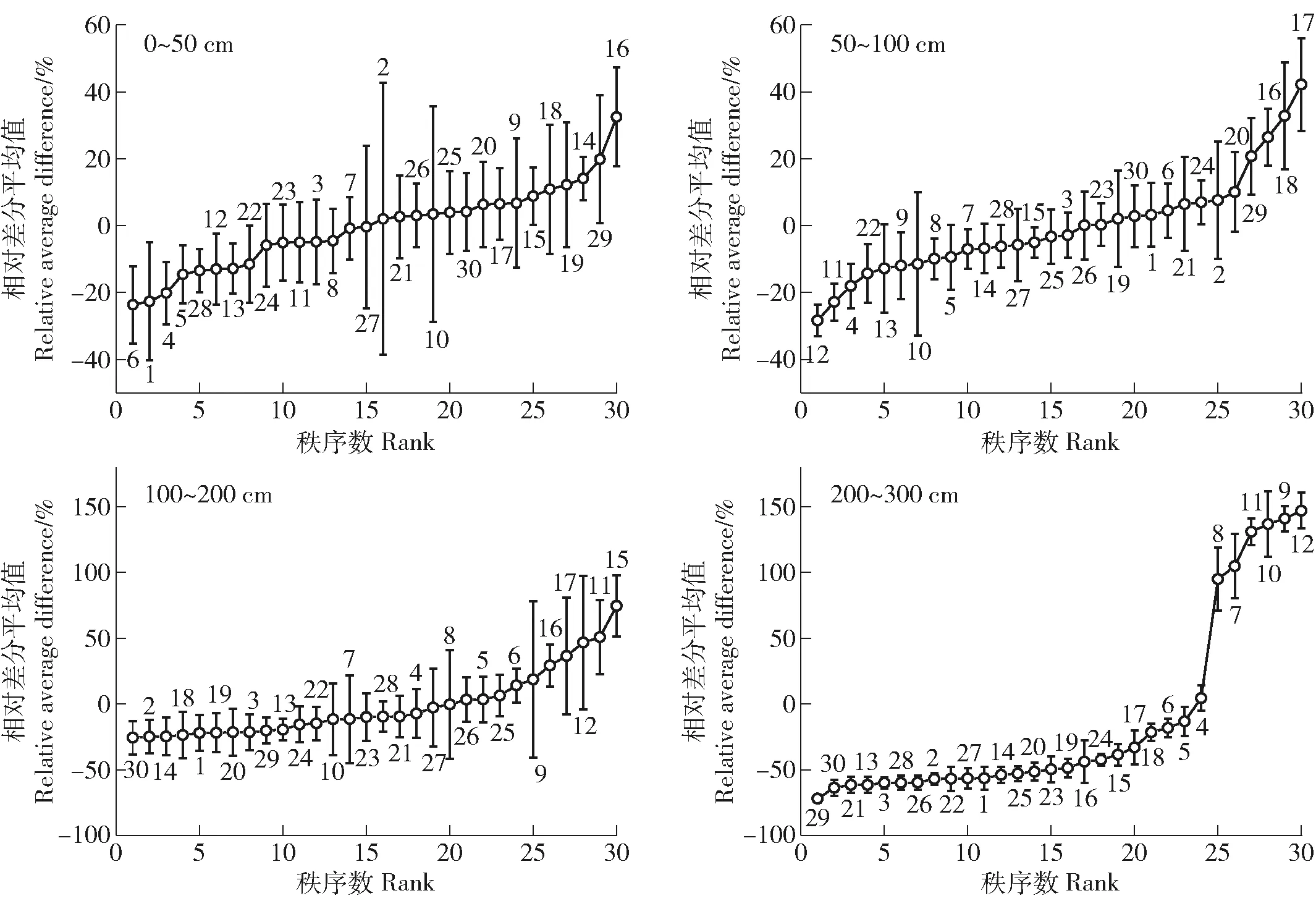
图4 不同土层土壤含水量的相对差分平均值及标准差Fig.4 Mean value of relative difference and standard deviation of soil moisture content in different soil layers

RMSE为均方根误差，MBE为平均偏差。RMSE stands for root mean sequared error, and MBE for mean absolute error. 图5 平均土壤含水量与代表性测点土壤含水量关系的比较Fig.5 Comparison of the relationship between mean soil moisture content and soil moisture content at representative sampling point

根据相对差分平均值接近于0且标准差较小的原则，选择最佳代表性测点来估算研究区平均土壤含水量，但此方法在选择代表性测点过程中具有一定的主观性且仅从这个指标不能得到较高的预测精度。因此本研究将所有测点平均土壤含水量与研究区平均土壤含水量进行相关性分析(图5)，发现测点7、23、6和7分别在0～50、50～100、100～200和200～300 cm土层中土壤含水量R2最大，因此可作为最佳代表性测点。4个最佳代表性R2变化范围为0.63～0.90，且各土层土壤含水量均方根误差和平均偏差分别为0.04～1.41和-0.12～0.97，表明研究区代表性测点与相应土层平均土壤含水量相关性较高，可以较准确的估计研究区平均土壤含水量。

3.5 长柄扁桃灌丛小区蒸散耗水量变化

从图6可以看出，坡面灌丛小区蒸散耗水量变化趋势与同期降水量具有较好的一致性，即随着监测期内降水量的增加而增大。2018年灌丛小区蒸散耗水量随着长柄扁桃生育期的推进，小区蒸散耗水量整体表现为先减小再增大后减小再增大并在7月17日—8月17日期间达到最大值(239.06 mm)；2019年整体上表现为先增大再减小，与2018年相比其波动趋势较小，这主要与降水量有关，灌丛小区蒸散耗水量最大值出现在7月1日—8月8日时间段(89.36 mm)。通过计算灌丛小区累积蒸散耗水量发现，2018年迎风坡坡面灌丛小区蒸散耗水量为517.10 mm，同期降水量为595 mm，灌丛小区土壤水分盈余77.9 mm；2019年迎风坡坡面灌丛小区蒸散耗水量为367.48 mm，同期降水量为315 mm，土壤水分亏损52.48 mm；2年监测期内迎风坡坡面灌丛小区蒸散耗水量为442.29 mm(均值)，同期降水量为455 mm(均值)，土壤水分盈余12.71 mm(均值)。总的来说，研究区迎风坡灌丛小区蒸散耗水量最大值出现在7月初—8月中旬，监测期内降水量大于灌丛小区蒸散耗水量，能够满足长柄扁桃灌丛小区正常生长。

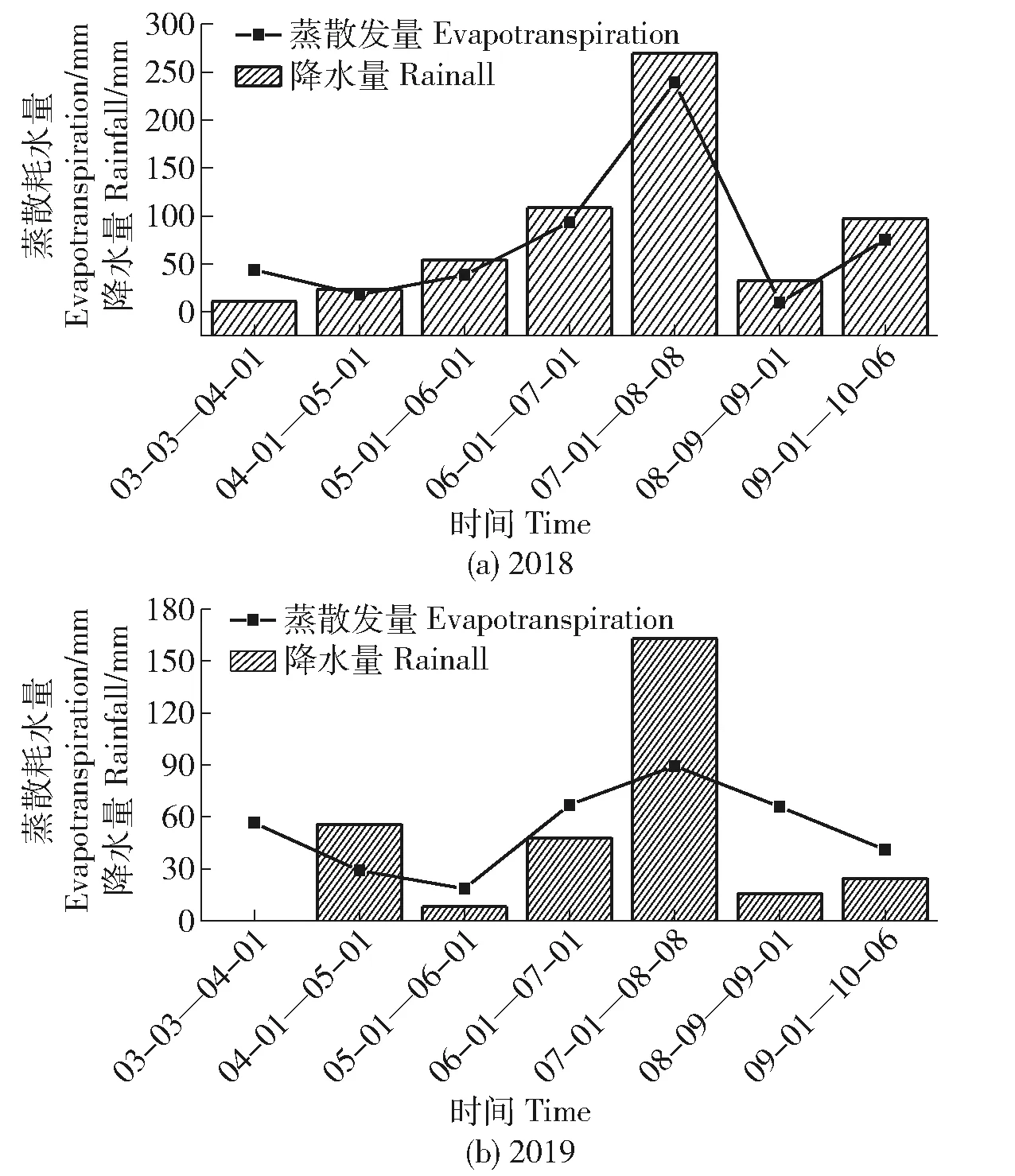
图6 灌丛小区蒸散耗水量与同期降水量时间变化Fig.6 Temporal variation of water consumption via evapotranspiration and rainfall in shrub communities

4 讨论

4.1 影响长柄扁桃林地剖面土壤水分空间变化的因素

试验结果表明各土层土壤含水量平均值随着土壤深度增加而增大，这可能是因为研究区坡面12 a林龄长柄扁桃灌丛林盖度较低(55%)，其冠层截留能力较弱，降水多以穿透雨和茎干流的形式汇聚植被基部土壤，加之坡面坡度较缓(3.3°)，土质疏松，入渗量大，难以形成地表径流[19]，土壤水分多以垂直运动为主，深层土壤水分得到有效补给，另外，在180～280 cm土层范围内存在多年累积的腐殖质层(有机质质量分数1.54 g/kg)，起到一定的保水作用[15，20]，因此浅层土壤水分较低，深层土壤水分较高。空间异质性是由样带尺度内多种因素相互作用的结果，植被恢复、人类活动等因素会使土壤质地较同一化发展，进而降低土壤水分在空间上的异质性,本研究区为人工生态林恢复坡面，由于生态环境的改善，人类和动物较频繁的活动使表层土壤水分在空间变异程度有所降低，同时植被根系选择性耗水也会降低土壤水分在空间上的变异性[21]，100 cm以下土壤结构基本未受扰动，自然形态下土壤性质如颗粒大小、有机质含量等在空间分布差异较大(表2)，因此浅层平均土壤含水量变异系数(空间变异系数)较深层较小。

4.2 影响长柄扁桃林地剖面土壤水分时间稳定性因素

本研究中2019年5月0～300 cm土壤水分秩相关系数较低(0.142～0.598)，这可能是因为测定前2 d发生降水(14.4 mm),且该时期土壤蒸发与植被蒸腾能力逐渐增强，干湿交替状态下的土壤水分波动较大，导致土壤水分秩相关系数不高，时间稳定性较差[9]。降水是研究区土壤水分补给的主要方式，由图2可知，监测期内降水量主要集中在7—9月且分别占2018和2019年全年降水量的70.19%和63.28%，降水分布不均导致各土层土壤含水量随时间波动较大，即各土壤含水量变异系数平均值均>10%。在监测期内，浅层土壤含水量变异系数平均值较高，深层较低，这与累计概率函数中深层保持相同概率土壤水分测点较多且相对差分标准差较小结果意义相同。这可能是因为浅层的土壤水分处于大气与土壤临近界面，是土壤水分中较活跃的土层，而深层土壤因浅层土壤的保护受外界因素影响较小，加之研究区降水事件多以脉冲式发生，发生的降水强度、持续时间具有随机性，这种特征会导致浅层土壤水分呈现不连续的脉动状态，因此降水的随机输入是浅层土壤水分波动较剧烈的最主要原因。随土层深度增加土壤水分时间稳定性越强，但其相对差分平均值变化范围却增大，两者并不矛盾。统计分析时得到土壤水分空间变异随土层增加而增强，空间变异系数越强，各测点土壤含水量相应分散，平均值的偏离程度也会越大，其相应的变化范围也增大。同时，研究区可用4个代表性测点的平均土壤含水量分别估算区域各土层土壤水分平均值，许多学者也得到相同的结论，如朱旭超等[22]在高寒草甸区、丁聪等[9]在高寒丘陵区、赵文举等[23]在西北压砂地发现，利用时间稳定性分析方法，可以获取估算研究区平均土壤含水量的某一代表性测点。从水量平衡角度分析，在监测期内研究区年际降水量变化较大，但2年降水量平均值大于灌丛小区蒸散耗水量，表明长柄扁桃灌丛对土壤水分的涵养大于其消耗，降水能够满足长柄扁桃灌丛小区正常生长。因此，利用时间稳定性方法分析该研究区土壤水分基本状况，为进一步了解该区域长柄扁桃灌丛与土壤水分相互关系及区域水分管理提供便捷高效的途径具有重要意义。

5 结论

1)在整个观测期，200～300 cm土层土壤含水量较高且与其他各土层差异性显著。随着土层深度增加，土壤含水量的空间变异性逐渐增强，时间变异性则相反，各土层土壤含水量在时空上均属中等变异。

2)Spearman秩相关系数表明，各测定时间对之间具有显著性差异(P<0.01)。在降水较多的年份，土壤含水量的空间模式在时间上具有更高的时间稳定性；干湿交替时，土壤水分时间稳定性较差。

3)土壤含水量时间稳定对土层深度和空间尺度具有较强的依赖性。结合累计概率函数、相对差分分析，土壤含水量的空间模式在时间上的稳定性随土层深度增加而增强。测点7、23、6和7分别代表研究区测定时段0～50、50～100、100～200和200～300 cm土层的平均土壤含水量，为准确、快速掌握研究区平均土壤含水量提供了便捷途径。

4)通过水量平衡分析表明，在监测期内灌丛小区蒸散耗水量与降水量变化较一致性，研究区迎风坡灌丛小区蒸散耗水量最大值出现在7月初—8月中旬，监测期内长柄扁桃灌丛对土壤水分的涵养大于其消耗，降水能够满足长柄扁桃灌丛小区正常生长。