黄土高原坡面土壤水分特征及时间稳定性
——以延安市九龙泉沟为例
2022-01-06单玉琳解建仓韩霁昌董起广
单玉琳, 解建仓, 韩霁昌, 雷 娜, 董起广
(1.西安理工大学 西北旱区生态水利国家重点实验室,710048,西安;2.陕西省土地工程建设集团有限责任公司,710075,西安)
土壤水对于研究区域地表径流、水分入渗、土壤侵蚀、溶质运移等过程具有十分重要的作用[1],但其时空变异性大,难以准确预估[2];因此,关于土壤水分分布特征及时间稳定性方面的研究一直备受关注,为更好地服务区域生态建设及水资源管理,诸多学者对不同区域土壤水分时间稳定性都开展了深入研究[3-4]。
我国黄土高原是典型的半干旱生态脆弱地区,而土壤水分是该区域植物生长和植被恢复的主要限制因子;长期造林过程中不合理的植被选择和栽植密度不但使林地土壤干化[5-6],也影响该地区水土保持的实施效果。黄土高原生态恢复及综合整治可以改变部分区域的地形条件、植被覆盖、土壤结构等,同时对区域水文循环过程及水资源时空分配产生较大影响[7],进而改变土壤水分的时空分布特征;因此,研究黄土高原坡面土壤水分的时间稳定性,合理制定区域植被结构,可为该区域水土保持及生态建设科学决策提供理论依据。
1 研究区概况
选择黄土高原一典型坡面进行研究,研究区位于陕西省延安市南泥湾镇的九龙泉沟流域,属梁峁丘陵沟壑区。沟道内海拔为1 170~1 100 m,南北长9.8 km,属温带季风气候区,冬季寒冷干燥,夏季炎热多雨,降水时空分布不均,季节变化大,主要集中在每年的7—9月,占到全年降水量的50%以上,多年平均降水量573 mm。区域土壤主要为黄绵土和灰褐土,沟道内为整治后的旱田及部分水田,坡面植被主要以灌草地及林地为主。
2 材料与方法
2.1 样点选择及测试方法
研究区域山体走向为南北方向,试验区坡面坡向为西向半阳坡,坡度20°。分别选取上坡位(U1、U2、U3、U4)、中坡位(M1、M2、M3、M4)、下坡位(L1、L2、L3、L4)各4个监测点进行土壤水分定位观测,坡面地表植被全部为天然次生灌木林及荒草地,研究区地理位置及土壤水分监测点布设如图1所示。土壤水分采用TRIME-PICO TDR进行定位监测。观测深度为0~100 cm,测量深度间隔为10 cm。分别于2017年的5月9日、6月14日、8月12日、9月18日进行4次土壤水分测定,每次测定重复3次。
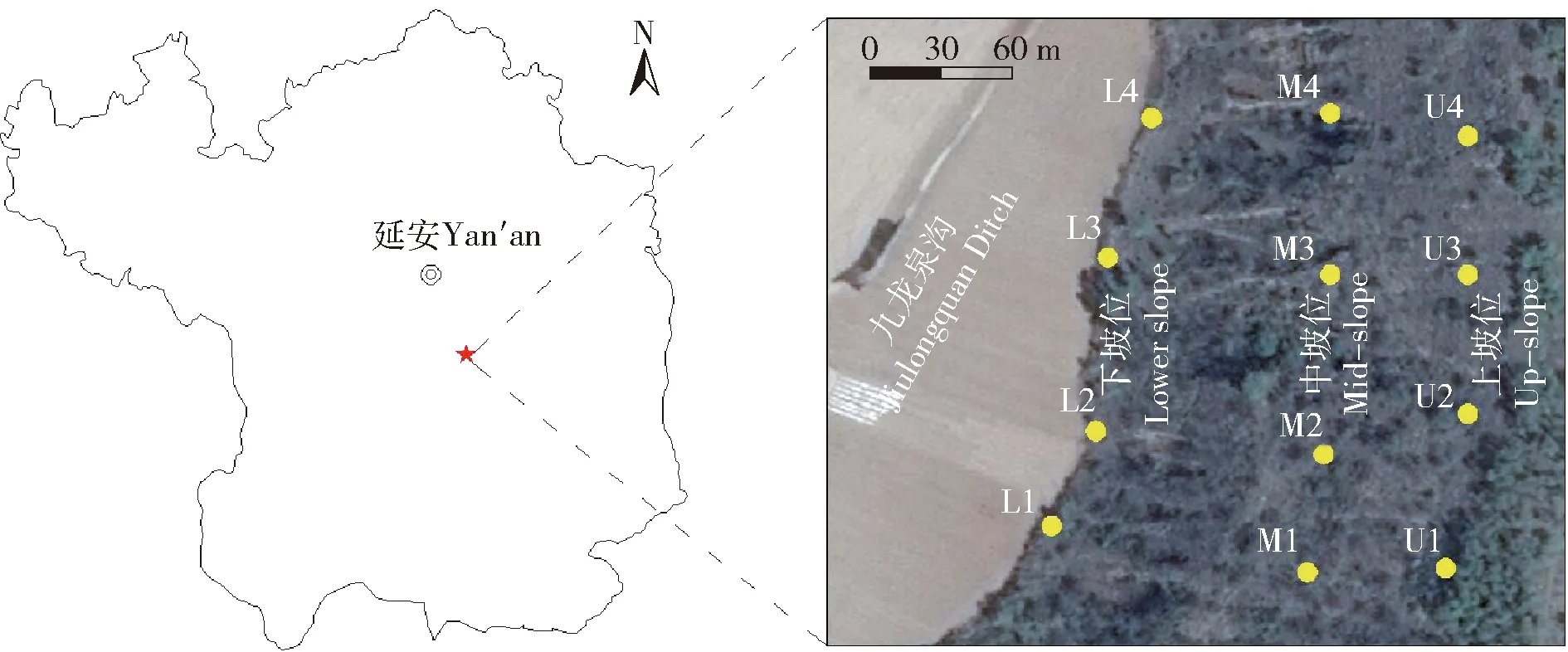
图1 研究区位置及监测点布设Fig.1 Location of the study area and monitoring points
2.2 数据分析方法
2.2.1 经典统计方法 变异特性的大小反映随机变量的离散程度,可用变异系数Cv来表示,当Cv<10%时为弱变异性、10%≤Cv≤100%为中等变异性,Cv>100%为强变异性[8]。
2.2.2 秩相关系数 Spearman秩相关系数法可以用来表示监测点土壤水分在不同时间上的相似性,公式为:
(1)
式中:rs为秩相关系数,值越接近1,则土壤水分的时间稳定性越强;Rij、Rij′分别为监测点i在时间j和j′下土壤含水率测定值的秩;N为监测样点数量。
2.2.3 相对差分 相对差分用来判断某一测点土壤含水率与研究区内9个样点平均土壤含水率的接近程度,公式为:
(2)
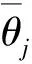
(3)
式中M为观测次数。
2.2.4 时间稳定性最佳代表测点判定方法 分别采用时间稳定性指数、相对差分平均值等参数用于判定含水率的时间稳定性最佳代表测点。
利用Jacobs等[9]提出的时间稳定性指数(Its),进行时间稳定性代表点的判定,计算公式为:
(4)
平均绝对偏差(MABE)及均方根误差(RMSE)也可用来进行时间稳定性代表点的判定,二者数值最小的点可作为时间稳定性最佳代表点。MABE及RMSE的计算公式如下:
(5)
(6)
3 结果与分析
3.1 土壤含水率的变异性
图2反映不同坡位各监测点土壤含水率4次测定结果的平均含水率、标准差及变异系数随土层深度的变化规律。土壤含水率的变异系数在不同坡位及不同深度上波动较大,而标准差及平均值则相对稳定。土壤含水率平均值随土层深度的增加呈现增大趋势,土壤水分标准差均<5%。上坡位与中坡位土壤含水率变异系数整体上表现为随着土层随深度的增加而减小,下坡位则表现为先减小后增大的变化趋势,且上、中坡位在0~50 cm土层为多中等变异性,下坡位则除50 cm、70 cm处外,各层均为中等变异性。

图2 不同深度下土壤含水率平均值、标准差及变异系数Fig.2 Average, standard deviation and coefficient of variation of soil moisture at different depths
不同坡位土壤含水率的平均值、标准差及其变异系数见图3。可见,不同坡位下的土壤含水率平均值表现为:上坡位<中坡位<下坡位。双侧t检验表明,上坡位与中坡位间土壤水分含量差异不显著,而下坡位与上、中坡位差异均显著(P<0.05)。不同坡位土壤含水率变异系数表现为上坡位、中坡位变异性较大,下坡位变异性较小,三者变异系数分别为15.77%、17.65%和13.57%,均为中等变异。
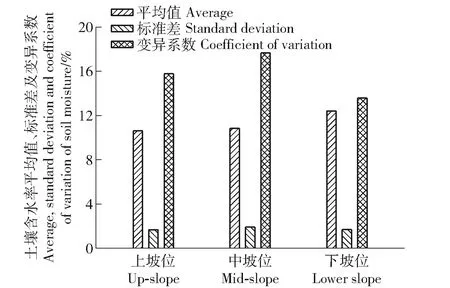
图3 不同坡位下土壤含水率平均值、标准差及变异系数Fig.3 Average, standard deviation and coefficient of variation of soil moisture at different slope positions
3.2 土壤水分时间稳定性
表1为不同深度土层土壤含水率平均值Spearman秩相关系数。0~100 cm土层土壤含水率的相关性最好,其次为0~50 cm,最低为50~100 cm。在0~50 cm范围土层,5月的含水率与其他监测时间的相关性较弱(P>0.05),而6、8、9月之间该层土壤含水率具有较高的稳定性,相关性极显著(P<0.01);50~100 cm土层土壤含水率仅在5、6月间具有显著的相关性;而0~100 cm范围土层的土壤含水率的稳定性最高,在5、6月,6、8、9月间均具有较显著的相关性,相关系数在0.383~0.786之间。
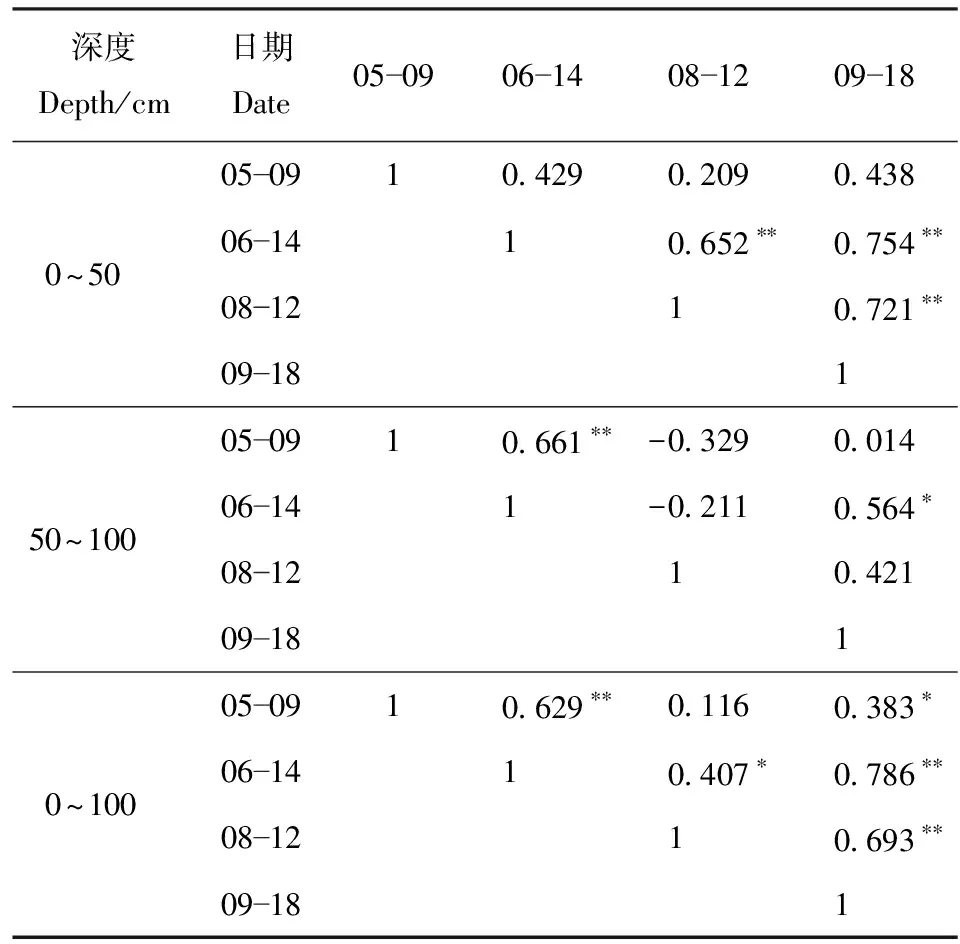
表1 研究区0~100 cm土壤含水率Spearman秩相关系数计算结果Tab.1 Calculated results of Spearman rank correlationcoefficient of soil moisture from 0 to 100 cmin the study area
不同坡位下土壤平均含水率Spearman秩相关系数见表2。在研究时间段内,上坡位秩相关系数范围为0.164~0.879之间,中坡位为0.394~0.745之间,下坡位为-0.754~0.744之间。整体上,土壤水分的时间稳定性由高到低为:中坡位、上坡位、下坡位。
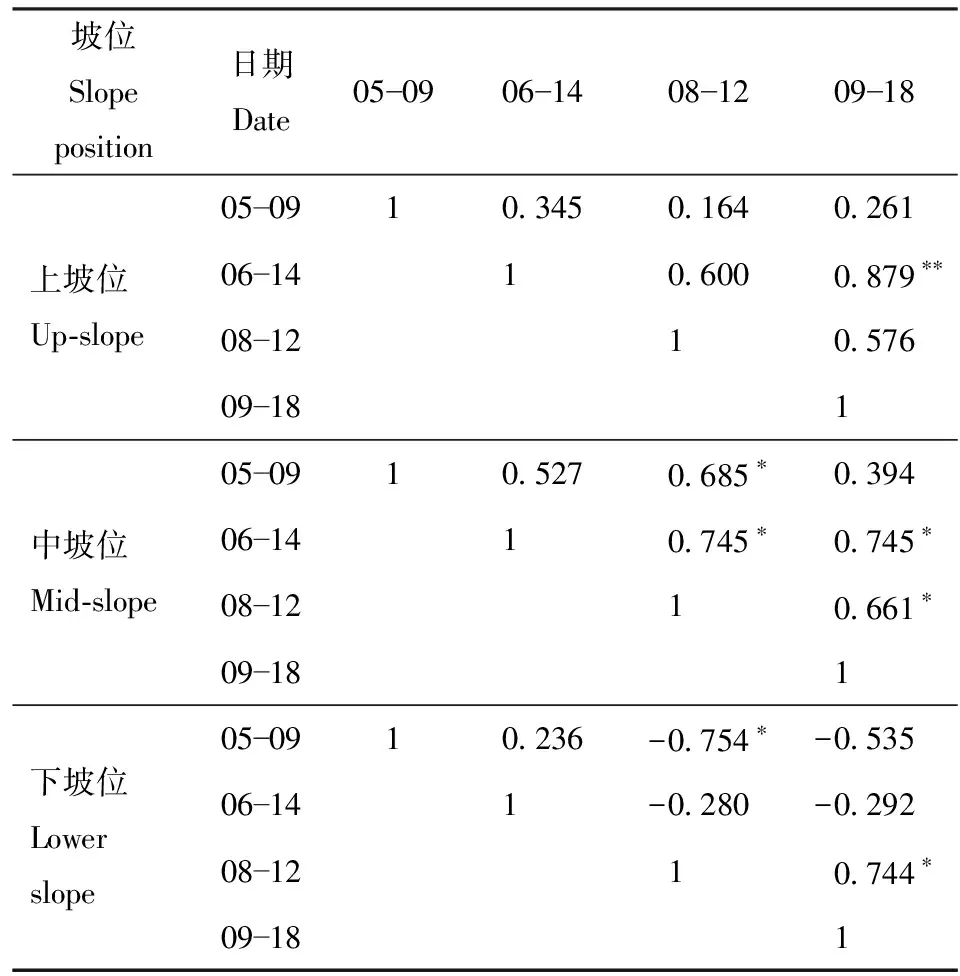
表2 不同坡位土壤含水率的Spearman秩相关系数Tab.2 Spearman rank correlation coefficient of soilmoisture at different slope positions
3.3 土壤含水率的相对差分及时间稳定性点分析
图4为各监测点土壤含水率相对差分平均值从小到大排列情况及对应的标准差。0~100 cm土层含水率的平均相对差分值范围为-18.3%~23.7%,平均值为1.6%。相对差分标准差范围为1.8%~9.9%,均值为6.4%。可见,位于中坡位的M3号点的相对差分值最接近于0,为-3.7%。图5至图7分别为时间稳定性指数、平均绝对偏差、均方根误差从小到大的排序图,由图可知,土壤水分时间稳定性指数<10%的测点共4个,均位于中坡位,最小的为M2号测点,值为4.1%。平均绝对偏差及均方根误差中,M3号点值均最小,分别为3.2%和2.6%。
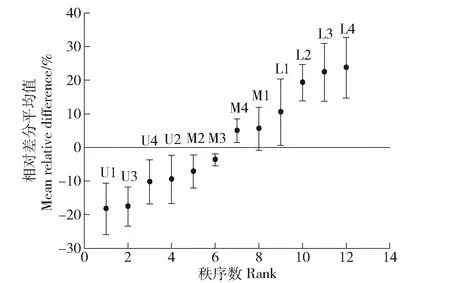
图4 土壤含水率相对差分平均值排序Fig.4 Ranking of mean relative difference of soil moisture
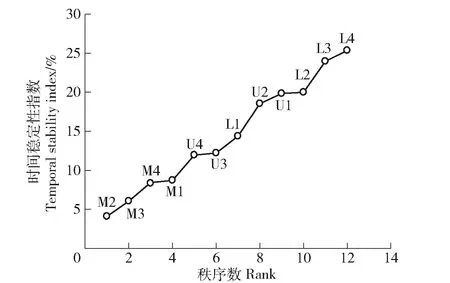
图5 土壤含水率时间稳定性指数排序Fig.5 Ranking of temporal stability index of soil moisture
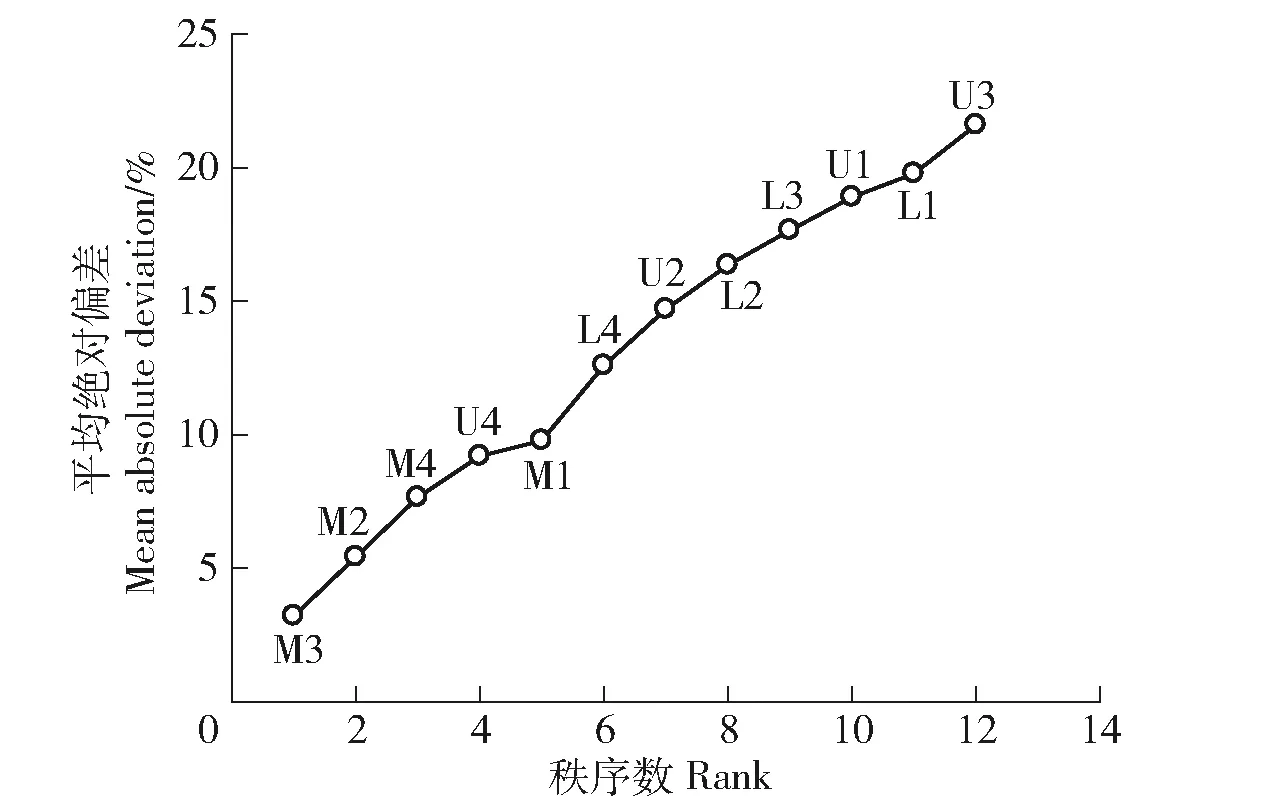
图6 土壤含水率平均绝对偏差排序Fig.6 Ranking of mean absolute deviation of soil moisture
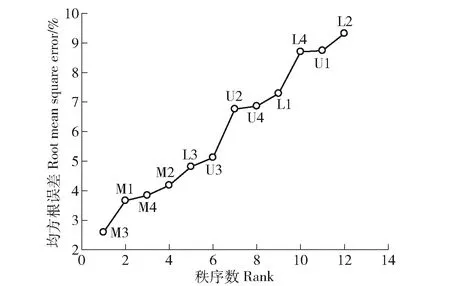
图7 土壤含水率均方根误差排序Fig.7 Ranking of root mean square error of soil moisture
表3分别对样地土壤含水率的平均值与测点含水率的线性决定回归系数(R2)、均方根误差(RMSE)、纳什系数(NSE)进行估算,结果显示M3号点具有较大的R2和NSE值及较小的RMSE值。综合以上方法,得到土壤含水率时间稳定性最佳测点为M3,该测点与研究区实测平均值的误差较小,为0~100 cm土层最优的时间稳定性代表性测点。在本研究中4种用于时间稳定性代表点确定的方法均能得出相对可靠的结果,而时间稳定性指数法在本研究中偏差略大于其他3种方法。
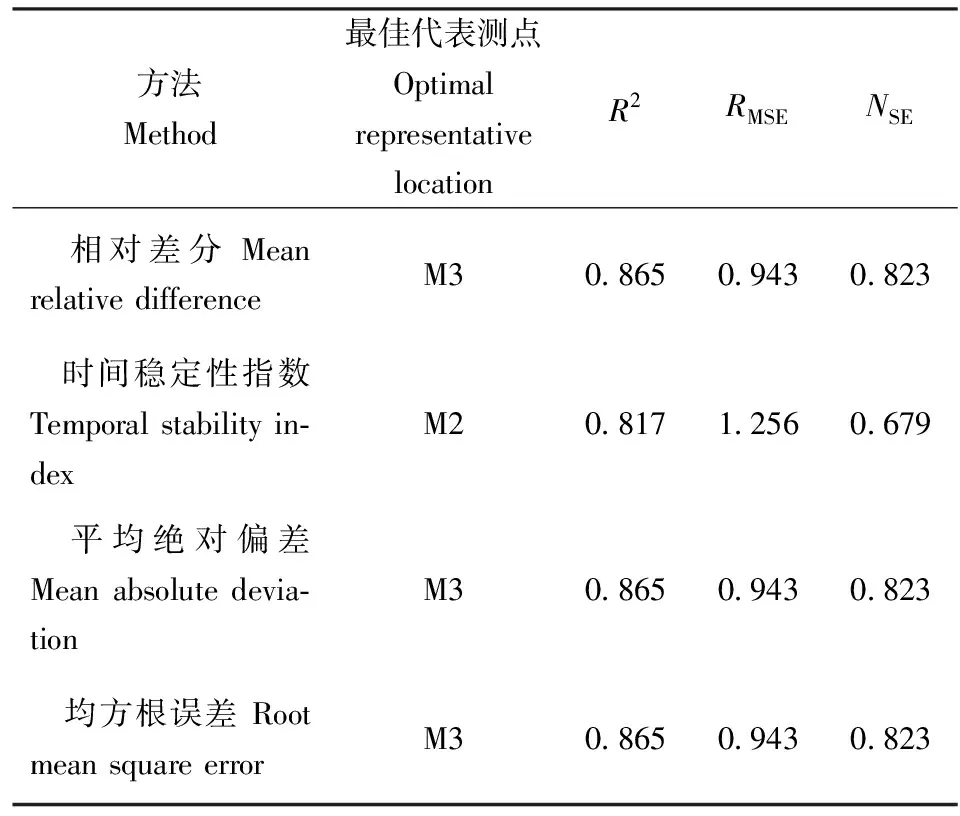
表3 不同方法对平均土壤含水率的估算精度Tab.3 Estimated accuracy of average soil moisture bydifferent methods
4 讨论
土壤水分含量从上坡位至下坡位逐渐增加,在垂直剖面上随土层深度的增加而增加,这种变化趋势主要受水分入渗过程及地形条件的影响,下坡位得到的水分补给更多,而深层土壤受蒸发及作物根系的影响较小,水分消耗少[10],这与何子淼等[11]关于土壤水分的垂向分布及坡向分布研究的结论类似。
Cv值在上坡位及中坡位表层较大的原因主要是表层土壤受蒸发及作物蒸腾因素的影响较大,这种趋势与Zhang等[12]的研究相似,土壤水在垂直剖面上可以分为不同的活跃层次;而在下坡位Cv表现出深层较大的原因则可能是地表径流及壤中流的不均匀补给引起的。
多数研究认为土壤含水率的时间稳定性随土层深度及平均水分含量的增加而增大[13],而本研究中0~50 cm土壤含水率在时间上的秩相关系数大于50~100 cm,下坡位土壤水时间稳定性小于中坡位,原因可能是研究区域的地形、土壤等条件使坡面易产生优先流,从而改变了深层土壤水时间稳定性,而下坡位更加接近沟道整治后的农田,可能受到农田灌溉及上坡水分补给的综合影响。同时,相对较大的人为干扰也可能是造成其时间稳定性较低的原因之一,这与张帅普等的研究类似[4]。整体上,5—6月相对干旱,植物消耗也较少,6—9月蒸发及植物消耗降水较多,所以相关性较好。
朱绪超等[14]认为,在较干和较湿的测点,土壤含水率的时间稳定性相对较弱,本研究中中坡位的土壤含水率更加接近研究区的平均值,且具有较高的时间稳定性,与其结论研究相同。同时,土壤水分时间稳定性还受土壤的结构与性质、植物根系活动及人类活动等共同影响[15-16]。因此,在后期的研究中应增加对黄土高原流域土壤性质变化及农业活动等方面对时间稳定性的长期影响分析。
5 结论
1)土壤含水率平均值随土层深度的增加而增大,土壤含水率变异系数在上坡位和中坡位上随深度的增加而减小,在下坡位上则呈现先减小后增大的趋势。在不同坡位上,土壤含水率表现出上坡位<中坡位<下坡位的趋势。
2)Spearman秩相关系数法分析土壤含水率的时间稳定性显示,0~50 cm土层土壤5月的含水率与其他监测时间的相关性较弱(P>0.05),而6、8、9月之间具有较高的稳定性,相关性极显著(P<0.01);50~100 cm范围土层土壤含水率仅在5月、6月间具有显著的相关性;0~100 cm范围土层土壤含水率则在5~9月各月份间均呈现显著相关性。
3)综合多种方法得出,研究区域内最佳时间稳定性点为中坡位的M3号点,该测点与研究区实测平均值的误差较小,为0~100 cm土层最优的时间稳定性代表性测点。
