钢板弹簧运动学特性研究

□ 刘保锋

三一建筑机器人(西安)研究院有限公司 西安 710200

1 研究背景

钢板弹簧的运动学特性影响汽车的操纵稳定性和平顺性,悬架与转向系匹配不合理,将会导致整车发生运动干涉[1-2]。钢板弹簧运动学特性研究的主要目的是获取钢板弹簧运动轨迹中心坐标及轨迹半径,校核理论计算结果[3],同时修正计算机辅助工程仿真模型,最终获得可用于悬架运动学分析与优化的理论计算模型和计算机辅助工程仿真模型。目前有关钢板弹簧的运动学研究主要集中在解析算法[3]、悬架运动学及柔顺性仿真分析[4-6],试验验证方案较少,对于多片簧钢板弹簧与少片簧钢板弹簧运动轨迹理论计算结果的差异性和准确性未知。

笔者通过台架试验、理论计算、计算机辅助工程分析方法,分别对多片簧钢板弹簧和少片簧钢板弹簧主片中心运动轨迹进行分析,确定理论模型的适用性,同时修正计算机辅助工程分析模型,对转向摇臂下球铰点的布置提出合理建议。钢板弹簧运动学特性研究思路如图1所示。

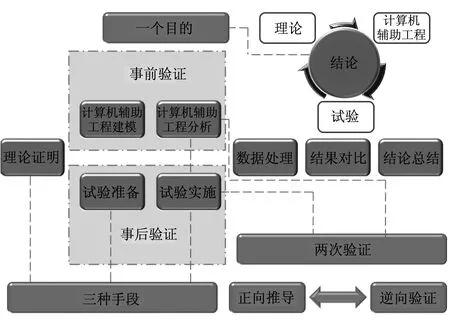
▲图1 钢板弹簧运动学特性研究思路

2 理论计算

对钢板弹簧进行运动学特征分析,最常用的方法是采用美国汽车工程协会圆弧理论。这一理论提供了钢板弹簧中心点近似运动轨迹,可以进行二维校核计算。美国汽车工程协会圆弧理论为:钢板弹簧第一片中心轨迹可以用以3l/4为半径,圆心位于比主卷耳中心高r/2的圆弧来近似描述[7-8],l为钢板弹簧的半长,r为主片中心线处卷耳半径,如图2所示。

▲图2 美国汽车工程协会圆弧理论

市场上主要的钢板弹簧类型有两种,为多片簧和少片簧[9]。为分析美国汽车工程协会圆弧理论的适用范围,选择两种多片簧钢板弹簧和三种少片簧钢板弹簧,对钢板弹簧主片运动轨迹中心坐标和轨迹半径进行理论计算,计算结果见表1。坐标原点为钢板弹簧主卷耳中心,X轴平行于汽车纵向指向后方,Z轴垂直于地面指向上方。

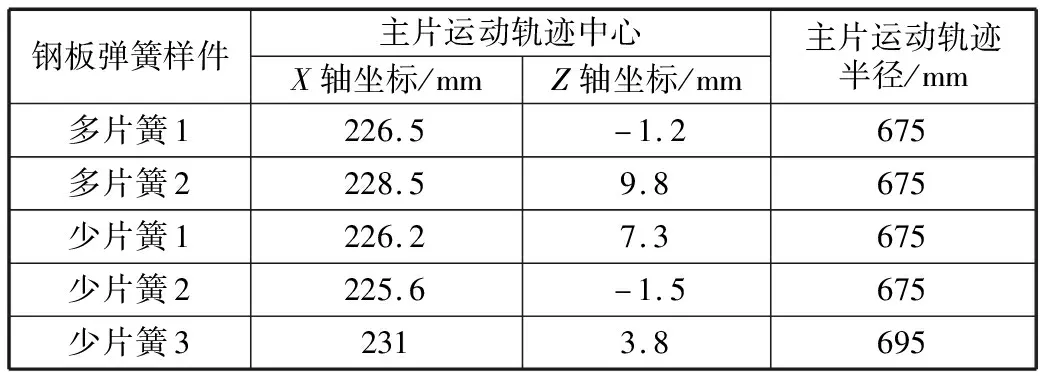
表1 圆弧理论计算结果

3 试验

搭建钢板弹簧主片运动轨迹中心专用试验台,如图3所示。确保纵梁、前卷耳、吊耳板、钢板弹簧夹板与实车位置及安装姿态一致,在纵梁、卷耳中心、主片中心粘贴反射片,通过三维激光扫描仪获取反射片坐标。将钢板弹簧安装在试验台上,检查U形螺栓、卷耳、吊耳板处的螺栓扭矩,保证与设计值一致。将钢板弹簧由自由状态加载至满载状态,重复三次,消除装配间隙。通过作动器加载,获取钢板弹簧竖直载荷与位移关系曲线,拟合得出钢板弹簧刚度。通过与设计刚度进行对比,判断钢板弹簧及台架是否符合技术条件。

确认五种钢板弹簧满足技术条件后,通过作动器加载,加载顺序为自由状态、极限位置、自由状态,加载位移见表2。分别测量钢板弹簧主片运动轨迹中心坐标和轨迹半径,测量结果见表3。

▲图3 钢板弹簧主片运动轨迹中心专用试验台

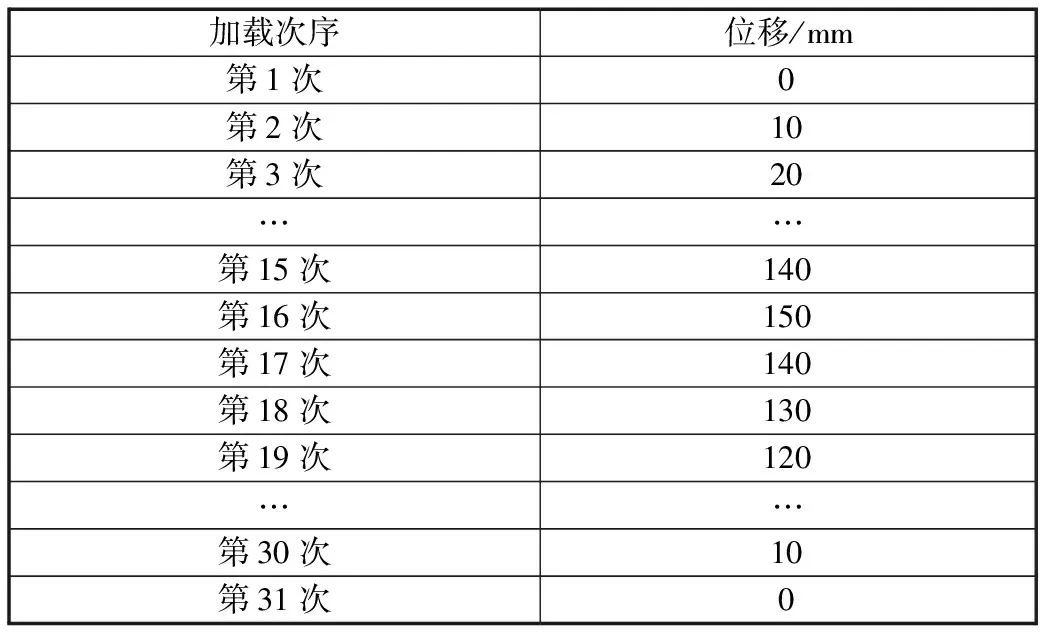
表2 加载位移

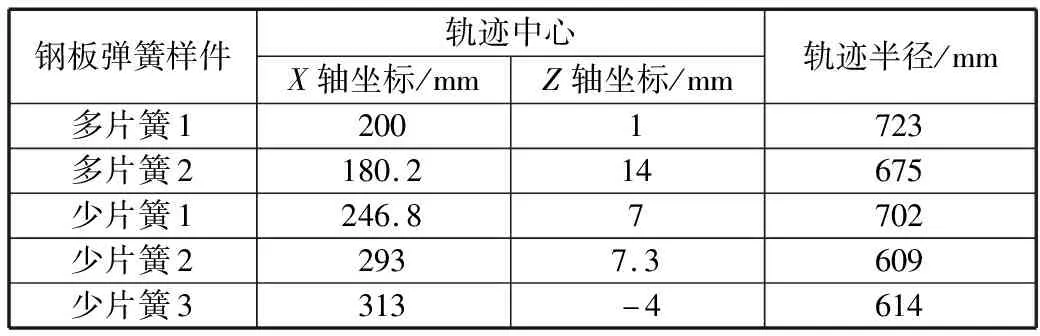
表3 钢板弹簧主片运动轨迹测量结果

4 理论计算与试验对比

将美国汽车工程协会圆弧理论计算结果与台架试验所得钢板弹簧主片运动轨迹中心进行对比。台架试验共测试五种钢板弹簧,每种钢板弹簧共三件样件,重复测量两次。多片簧钢板弹簧主片运动轨迹中心对比结果如图4所示。由图4可以发现,多片簧钢板弹簧理论计算与试验结果偏差主要为半径偏差。少片簧钢板弹簧主片运动轨迹中心对比结果如图5所示。由图5可以发现,少片簧钢板弹簧理论计算与试验结果偏差主要为角度偏差。

通过构建理论模型分析角度偏差、半径偏差导致的悬架系统对转向系统干涉量的影响,如图6所示。由图6可以确定,角度偏差引起的干涉量大,半径偏差引起的干涉量小。因此,试验点与理论计算点有偏差时,试验点在理论计算点与钢板弹簧主片中心连线上时,导致的干涉量最小。

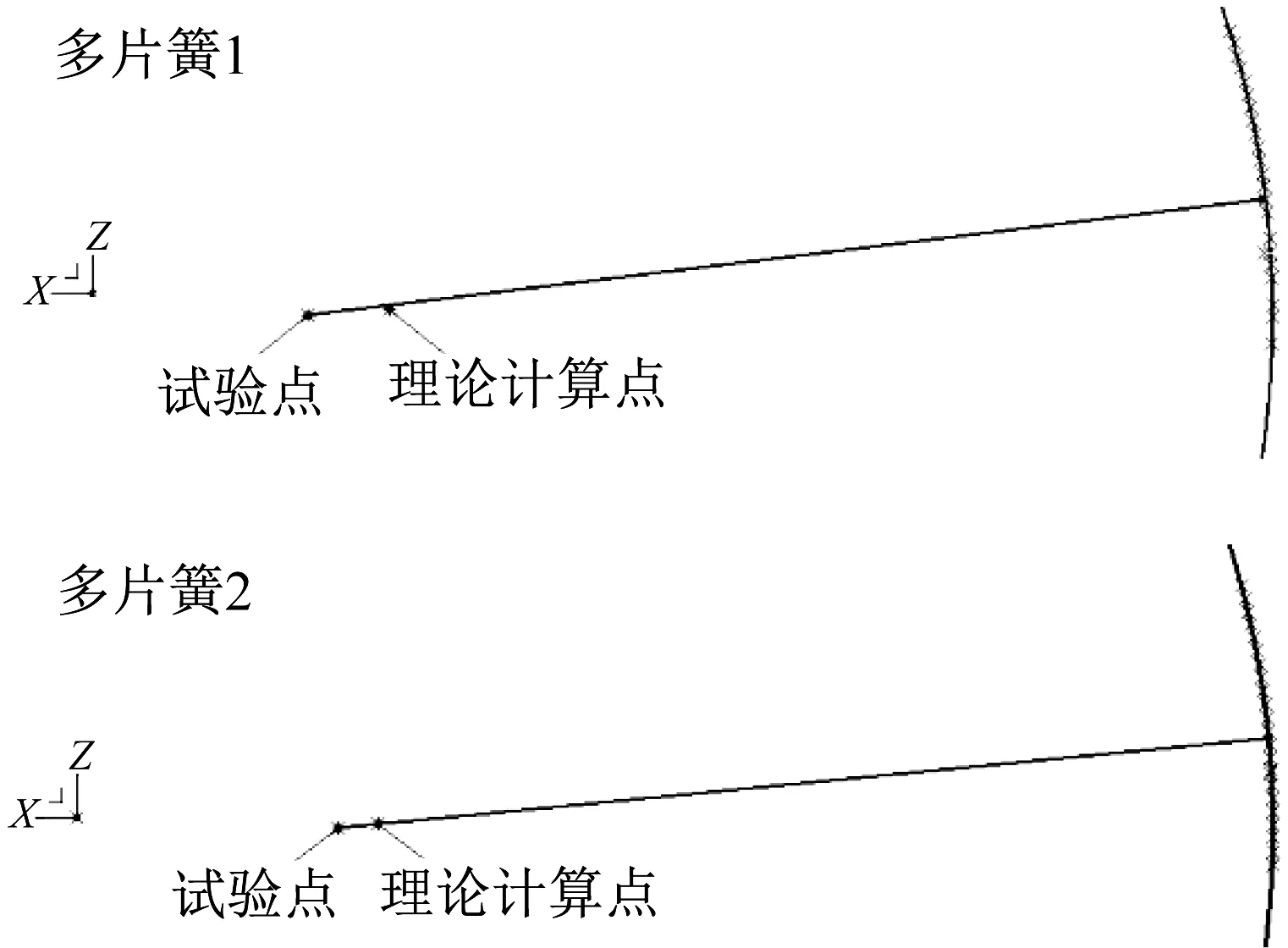
▲图4 多片簧钢板弹簧主片运动轨迹中心对比

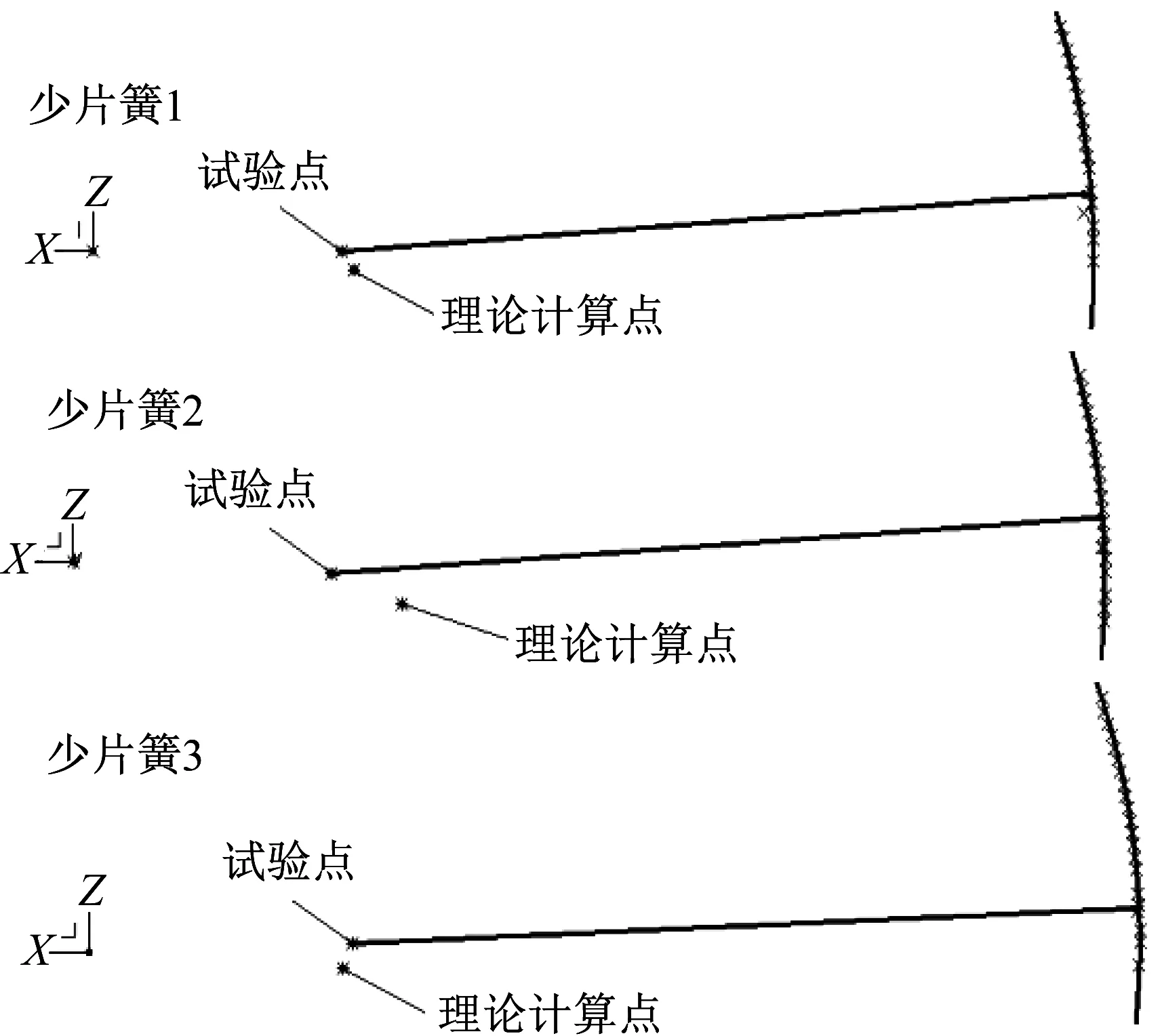
▲图5 少片簧钢板弹簧主片运动轨迹中心对比

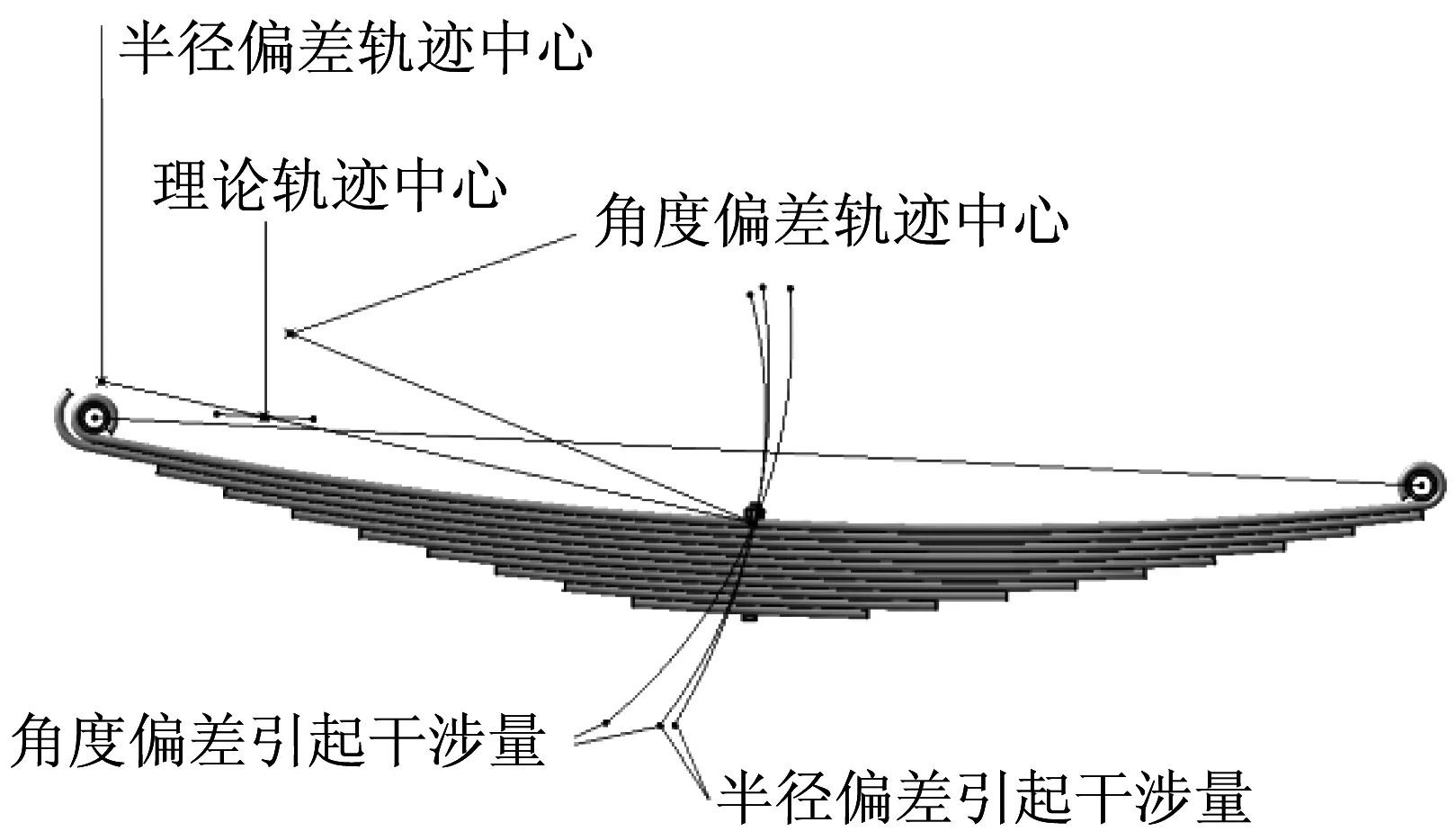
▲图6 偏差对干涉量影响

5 圆弧理论适用范围分析

根据理论分析结果可以确定,悬架与转向系统的干涉量主要由钢板弹簧主片运动轨迹中心角度偏差引起。为了寻求少片簧钢板弹簧与多片簧钢板弹簧角度偏差规律,并获得修正数值,笔者对理论计算与试验角度偏差结果进行统计,结果如图7所示。统计结果显示,多片簧钢板弹簧理论计算与试验角度偏差处于0°～0.3°,悬架系统匹配时可以直接使用美国汽车工程协会圆弧理论进行计算;少片簧钢板弹簧理论计算与试验角度偏差处于0.5°～1°,设计时需要对美国汽车工程协会圆弧理论计算结果进行修正。

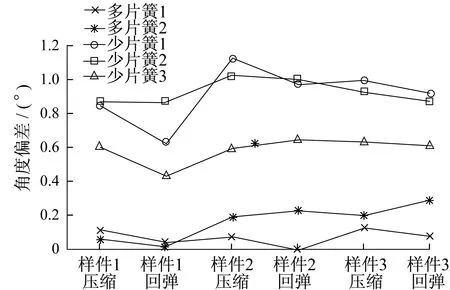
▲图7 角度偏差理论计算与试验统计结果

6 仿真分析

钢板弹簧建模时,对钢板弹簧进行逆向扫描,得到钢板弹簧安装状态和自由状态点云数据,根据点云数据建立钢板弹簧三维模型;依据自由状态下钢板弹簧的形状得到控制点坐标,根据控制点坐标在ADAMS软件中建立钢板弹簧模型;通过参数优化,完成模型修正[10-11]。钢板弹簧轨迹ADAMS软件分析模型如图8所示。以少片簧钢板弹簧1为例,对美国汽车工程协会圆弧理论计算、ADAMS软件仿真、台架试验得到的钢板弹簧主片运动轨迹中心进行对比,结果如图9所示。由图9可以发现,ADAMS软件仿真得到的钢板弹簧主片运动轨迹中心与试验高度符合,因此在后续车辆悬架系统仿真或进行问题整改时,可以直接使用这一模型。

▲图8 钢板弹簧轨迹ADAMS软件分析模型

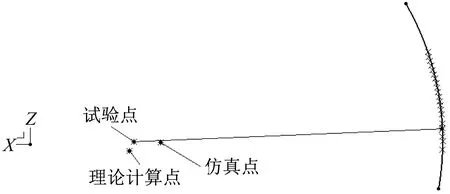
▲图9 少片簧钢板弹簧1主片运动轨迹中心对比结果

7 结束语

笔者利用台架试验、美国汽车工程协会圆弧理论对两种多片簧钢板弹簧、三种少片簧钢板弹簧的主片运动轨迹中心进行分析,结果表明,多片簧钢板弹簧理论计算与试验偏差为半径偏差,少片簧钢板弹簧理论计算与试验偏差为角度偏差,角度偏差引起的干涉量大,半径偏差引起的干涉量小。多片簧钢板弹簧主片理论运动轨迹中心与试验符合,悬架系统匹配时可以直接使用美国汽车工程协会圆弧理论进行计算。少片簧钢板弹簧主片理论运动轨迹中心与试验偏差较大,设计时需要对美国汽车工程协会圆弧理论计算结果进行修正。

在转向系统布置过程中,应保证转向悬架干涉量最小。对于多片簧钢板弹簧,转向摇臂下球铰点布置在转向节臂球铰点与钢板弹簧主片理论运动轨迹中心连线上。对于少片簧钢板弹簧,转向摇臂下球铰点布置在转向节臂球铰点与钢板弹簧主片理论运动轨迹中心连线偏0.5°～1°范围内。

通过ADAMS软件建模,确保仿真结果与台架试验结果一致后,可对不同悬架高度及钢板弹簧制动纵扭工况对悬架系统干涉的影响做进一步分析,为设计人员分析校核提供重要数据依据。