Popovic与Rado不等式的推广

2022-01-06刘小宁

武汉工程职业技术学院学报 2021年4期

关键词：算术锐角正数

刘小宁

(武汉软件工程职业学院湖北武汉： 430205)

设ai为正数，n为正整数，i=1，2，…，n，记

f(n)=n(An-Gn)

Popovic证明了F(n)是变量个数n的递增函数[1]，即存在如下不等式

F(n)≥F(n-1)≥…≥F(2)≥F(1)

(1)

等号当且仅当an=An-1时成立。

Rado证明了f(n)是变量个数n的递增函数[1]，即

f(n)≥f(n-1)≥…≥f(2)≥f(1)

(2)

等号当且仅当an=Gn-1时成立。

注意到F(1)=1与f(1)=0，由式(1)或式(2)可得到关于变量大小的算术—几何平均值不等式

An≥Gn

(3)

等号当且仅当a1=a2=…=an时成立。

式(1)或式(2)是关于变量个数的单调函数(不等式)，式(3)是关于变量大小的不等式。

基于将变量大小与变量个数这两个因素联系起来构建不等式的思路[1-3]，文中采用变量变换法，尝试建立有关变量个数的几个单调函数，并导出相应不等式。

1 定理

为讨论方便，设实函数R(x)变量x的定义域为(a，b)，βi为正数，i=1，2，…，n，记

定理若R(x)在定义域(a，b)内为凸函数，则

Q(n)=Pn[R(Sn)-Tn]

是变量个数n的递增函数。

证明：取xi和xi/分别为定义域(a，b)的两组变量，且xi和xi/的大小分别与变量个数n无关，根据凸函数定理，有

(4)

其中

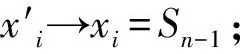
因为βnR(xn)=PnTn-Pn-1Tn-1

将其代入式(4)整理，可得到

Pn[R(Sn)-Tn]≥Pn-1[R(Sn-1)-Tn-1]

即Q(n)≥Q(n-1)

表明Q(n)为变量个数n的递增函数，定理成立。

2 推广

取定理中R(x)=lnx，若x的定义域为正数，因为R″(x)=-1/x2<0，故R(x)=lnx为凸函数，根据定理有

推广1：若xi与βi为正数，且xi和βi的大小分别与变量个数n无关，函数

是关于变量个数n的递增函数。

推广1是单调函数(1)关于n个正数的算术与几何加权平均值的推广，若作变换xi→1/xi，可得

推广2：若xi与βi为正数，且xi和βi的大小分别与变量个数n无关，函数

是关于变量个数n的递增函数。

推广2是单调函数(1)关于n个正数的几何与调和加权平均值的推广。

采用定理证明中作变换的方法，由推广1可得

推广3：若xi与βi为正数，且xi和βi的大小分别与变量个数n无关，记

则Q3(n)与Q4(n)分别是变量个数n的递增函数。

因为Q3(n)≥Q3(n-1)≥…≥Q3(2)≥Q3(1)=0，取其中β1=β2=…=βn=1，可得到单调函数(2)，因此，Q3(n)是单调函数(2)关于n个正数算术和几何加权平均值的推广；由于Q4(n)≥Q4(n-1)≥…≥Q4(2)≥Q4(1)=0，因此，可以认为Q3(n)是单调函数(2)关于n个正数算术和调和加权平均值的推广。

在推广3中作变换xi→1/xi，可得

推广4：若xi与βi为正数，且xi和βi的大小分别与变量个数n无关，记

则Q5(n)与Q6(n)分别是变量个数n的递增函数。

显然，Q5(n)是关于n个正数调和加权平均值倒数与和几何加权平均值倒数的递增函数，Q6(n)是关于n个正数调和加权平均值倒数与和算术加权平均值倒数的递增函数。