基于线性回归方法改进的KNN数据分类模型

2022-01-06李长生刘宗成

兰州石化职业技术学院学报 2021年3期

李长生，刘宗成，刘硕

(兰州石化职业技术学院信息处理与控制工程学院，甘肃兰州 730060)

分类算法是机器学习和模式识别中的重要研究内容之一，诸如贝叶斯网络算法、神经网络算法、决策树C4.5算法、SVM(支持向量机)算法、Random forest算法、Bagging算法、KNN算法等。其中，由于K最近邻算法[1](k-Nearest Neighbor，KNN)思想简单、容易实现、重新训练数据的较低代价、以及较高的分类准确率，使其在自动分类领域应用较广[2]。

KNN算法简单易懂，是一种理论上非常成熟的分类算法，但是KNN分类算法在遇到数据集规模较大或者维数较多的时候，会陷入维度灾难的情况，造成KNN模型的计算开销增大、分类效率降低。针对这一问题，许多专家学者提出在KNN算法运行之前预处理数据集，期望缓解这一问题，例如张著英等[3]将数据集用粗糙集进行预先处理，得到简约属性之后的数据集，然后用KNN处理以提高分类效率。张孝飞等[4]通过降低待分类对象与K个最近邻对象的相似性度量的计算量来提高分类效率。余鹰等[5]利用变精度粗糙集处理数据集，计算新样本集的归属区域，降低分类的代价，提高分类的效率。而在对数据集进行属性简约时，如何对原始特征集进行判断，得到最优的评估子集，在不降低分类精确度的前提下，利用这些评估子集更快的得到分类结果，这也是目前研究的一个热点，像陈珠英等[6]应用线性回归在2型糖尿病患者中剖析丙酮的影响因素，经由相关系数判别各个因变量对丙酮浓度的影响强弱。

此外，KNN分类算法通常采用欧式距离来计算训练集与待测样本集之间的关系，但不同特征量对分类结果准确性影响是不同的。针对这一问题，赵静等[7]通过对现有的基于信息熵和区间距离的不确定性度量公式进行优化，但这种方法运行效率有所下降；针对上述问题，本文采用线性回归简约数据集属性，利用卡方距离替换欧式距离，然后根据得出的特征向量影响强度赋予权重实验表明，改进后的算法与传统的KNN算法相比，在特征识别性能方面有了一定的提高。

1 相关算法概述

1.1 KNN算法

KNN是一种懒惰式的机器学习算法，算法思想是：当一个待分对象在训练集中与K个距离最近的实例中的max(K个样本)属于同一个类别，那么就把该测试集数据分到大多数实例所属类别中。其判断条件可以定义为公式：

fi(x)=max(k)，(i=1，2，…n) (1)

其中，i表示训练集中不同的对象，k表示K个数据样本。

1.2 卡方距离

K近邻算法中常用测距方法是欧式距离法，但是欧式距离只考虑各个属性间的绝对距离，会忽视各特征属性间的相对距离，而且会因为同等权量数据集中不同属性间的差异，导致不能满足实际需求中的要求；而卡方距离能有效反映各个属性间相对距离的变化，故利用线性回归计算各个特征向量对分类影响的强弱，从而弥补欧式距离对属性间距离量化的不足之处。

卡方距离计算公式如下所示：

1.3 线性回归

基于数理统计中的回归分析方法，通过对两个或者两个以上自变量与一个因变量的相关分析，建立模型预测结果。这里利用数据集的多维属性变量之间相互依赖的定量关系，然后根据变量之间的关系约简数据集属性。

(1)评估模型的拟合程度时需要计算判定系数R2，其公式如下：

(2)选择目标属性时可利用公式(4)计算Adjusted.R2(属性间的权重系数)，筛选出真正适合用于建模的属性集合。其公式如下：

式中n表示属性序列数，k表示变量数。

2 基于线性回归的改进KNN算法

本文首先利用线性回归方法简约属性集合，得到降维之后的较优特征属性集合，然后按照属性间的决定系数计算得到的各个特征向量对分类的贡献度，赋予不同的属性权值，卡方距离利用新的属性权值，得到KNN改进之后的样本距离，然后判断待分类对象的归属。

2.1 改进的KNN算法

基于线性回归方法改进的KNN算法的流程如图1所示.

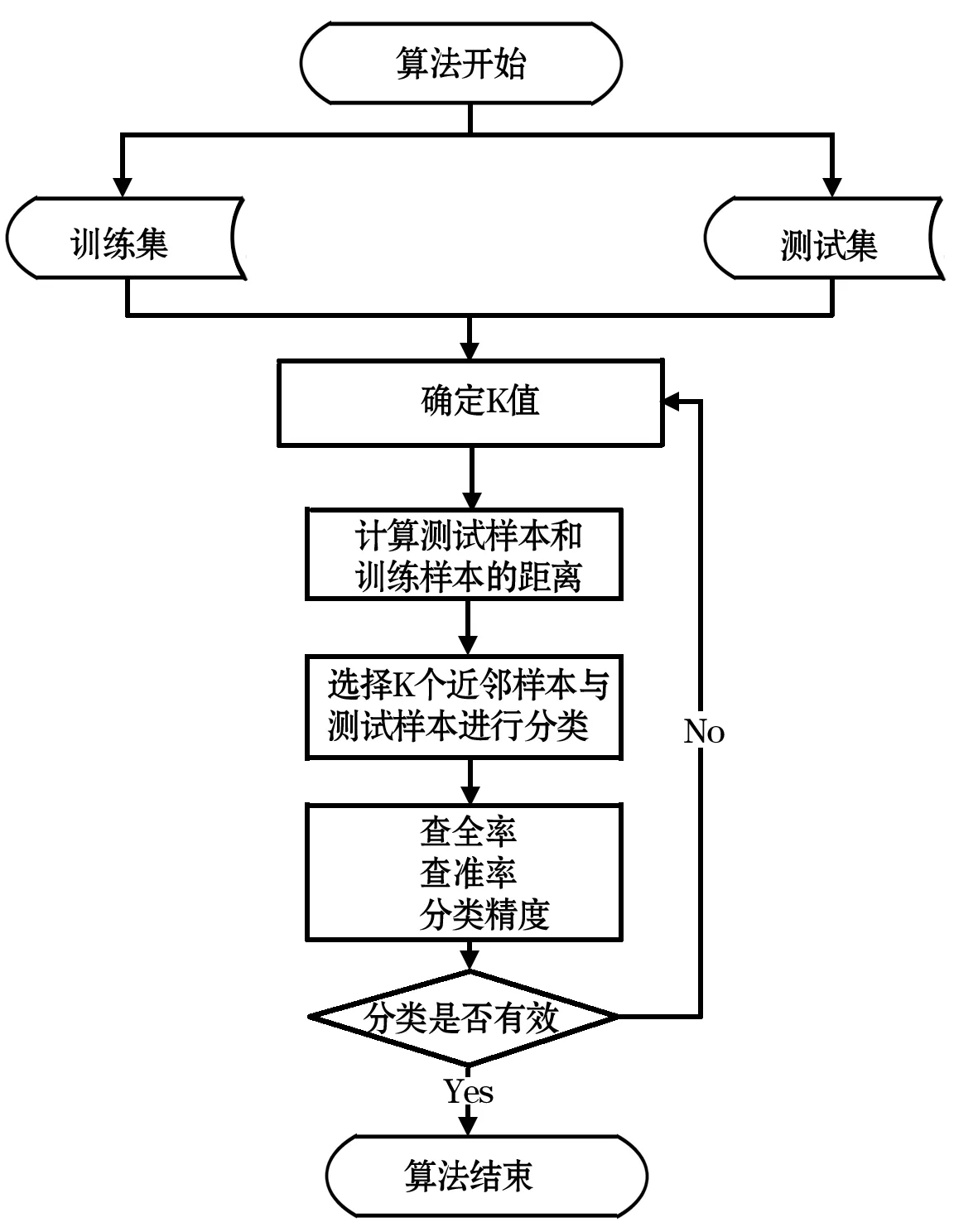
图1 算法流程图

具体步骤如下所示：

(1)首先将数据集进行清洗预处理，即清除缺失值、噪声数据、以及不一致的数据集，得到质量较高的有效数据集。

(2)应用线性回归方法处理清洗后的数据，即通过公式(4)计算出数据集各个属性之间的决定系数，从而筛选出合适的简约属性集合。

(3)创建测试集，将步骤二中的数据集，采用随机抽样的方法，选择3/4作为训练集X，剩余1/4作为测试集Y。

(4)给K随机创建一个初始训练值。

(5)利用公式(3)比较特征向量对目标变量的影响强弱，根据强弱确定属性权重的值。

(6)运用加权卡方距离计算测试集样本与训练集样本之间的加权距离。加权卡方距离公式如下：

式中，wi代表属性i的特征权重。

(7)选取K个训练样本，与测试集中待分类对象比较，通过公式(1)得到待分类对象的类别。在改进的KNN算法中，通过不断调整K的取值，得到每一个K值所对应的正确率，基于此正确率的折线图得到适合简约属性之后数据集的K值,如图2所示。由折线图可知，当K=6的时候，算法的正确率达到最高值，之后随着K的增加趋于平稳，所以选取K值为6。

图2 聚类K值的最优值分析

3 实验结果分析

实验基于Python语言集成开发平台PyCharm配置的机器学习环境进行研究。实验数据分别使用机器学习数据库UCI中的四个标准测试数据集和从甘肃省某医院采集的乳腺癌临床试验数据集。

UCI库中的四个标准数据集分别是breast cancer(乳腺癌)，heart disease(心脏病)，hepatitis(肝炎)和乳腺癌临床数据集，关于这四个具体的数据集的相关信息如表1所示。

表1 实验数据集的表现格式

采用改进算法对训练集和测试集处理后，计算平均召回率(recall)、平均精确率(precision)和准确率(accuracy)，作为评价分类算法的性能指标。

其中：ai表示在类中准确预测到的数目；bi表示测试样本中为类的总数目。

其中：ai公式(6)所示，ci表示预测为第i类的测试样本数目。

其中：a代表训练集样本中预测准确的样本数量；b表示总的样本数量。

实验数据集经属性简约之后的情况如表2所示。

表2 简约结果

由表2中的结果可以得出本文所改进的KNN算法较传统的KNN算法在简约属性上具有微弱优势，说明线性回归在属性简约上是有效的。

在保持K值相同的情况下，对测试数据集进行实验分析，结果如表3、表4所示。

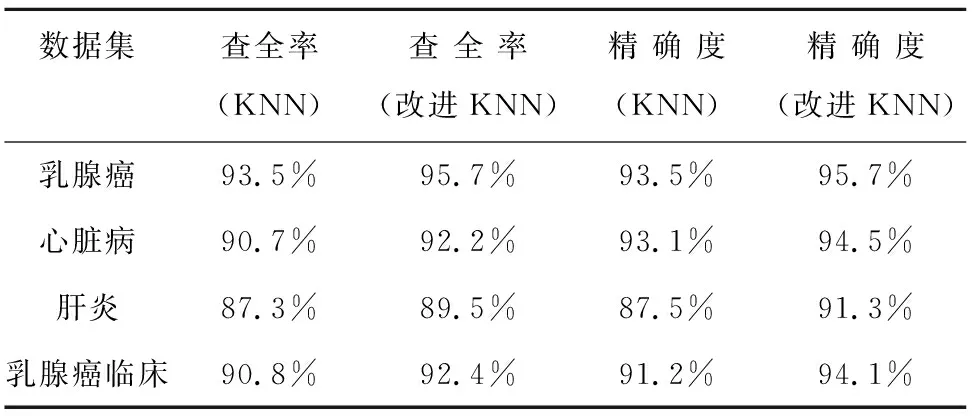
表3 K=6实验结果1

表4 K=6实验结果2

通过上述实验数据，当K=6时，改进KNN的方法在召回率率recall、精确率precision以及准确率accuracy的判断上都有了一定的提高，例如在心脏病数据集上，改进KNN算法的查全率要比传统KNN算法的查全率高1.5%，查准率比传统KNN算法高0.8%，精确度增加了1.4%，说明改进的KNN算法的各项指标均优于传统的KNN算法。