基于响应曲面法的双排桩支护结构优化设计

郭庆华， 蔡至琛， 王 莹

(1.山东省水利工程试验中心有限公司， 济南 250013； 2.水发规划设计有限公司， 济南 250013；3.山东省水利勘测设计院， 济南 250013)

在紧邻既有建/构筑物进行基坑支护，禁止采用排桩+锚杆支护结构时，如果悬臂支护结构难以满足基坑变形控制要求，传统的做法是采用排桩加支撑的支护结构。这种支护结构虽然能满足基坑变形控制要求，但其对基坑施工工期造成较大影响，并且经济性较差。因此，采用双排桩支护结构就成为理想的选择。

由支护桩、冠梁和前后排桩间的连梁组成的空间门式刚架支护结构体系具有较大的侧向刚度，可有效限制基坑变形[1]。其限制基坑变形的影响因素是多方面的，但主要是双排桩的尺寸及桩距、排距等。前期对于双排桩基坑支护的研究主要侧重于计算模型[2-5]、支护参数的研究[6-8]及单指标的结构优化[9-10]，对多指标的优化研究相对较少。马郧等[11]采用中勘之星设计软件进行了详细分析，认为双排桩基坑支护结构稳定性及变形受嵌固深度、桩径、桩距、前后桩排距、连梁尺寸、土体性质等多种因素的影响。欧孝夺等[12]通过分析设计参数改变对支护效果的影响，认为双排桩支护结构的最佳排距为4～6倍桩经;增大桩径，桩身位移的减小幅度不大。根据现场条件确定了双排桩支护方案后，就有一个如何选择结构设计变量，如桩径、桩长、嵌固深度、桩距、排距等，在满足变形要求及稳定性的条件下，使得结构材料最省的问题。董金奎[13]通过在双排桩腰部增设连系梁进行填方工程中双排桩的设计优化。姜开渝[14]利用杆系有限元，结合均匀试验和ACE非参数回归拟合技术构造目标参数和约束条件的响应面，运用枚举法进行多参数的双排桩优化。该方法对常用深基坑支护结构设计软件的设计人员不容易掌握，较难推广。况且以成本为目标函数，基坑稳定性系数及变形作为约束条件，影响因素多，建模难度大，计算复杂。现行的基坑设计方法多是将规范规定及合同要求作为约束，直接将基坑变形及稳定性安全系数作为方案是否可行的首要条件。这种方法直观、方便、实用。为此，在已有工作[15-16]的基础上，以一个一级基坑为例，用均匀设计安排不同结构尺寸组合的双排桩支护方案，将用理正深基坑支护结构设计软件模拟计算的基坑变形及稳定性安全系数回归方程作为目标函数，双排桩结构参数作为约束条件，从而提供一种简便实用的双排桩支护结构优化设计方法。

1 响应曲面法原理

1.1 结构优化设计

结构优化设计是在设计思想和结构分析的数学模型确定以后，利用结构优化设计的方法和计算机进行优选，以达到一定的设计目标[17]。即求设计向量x，使目标函数W(x)→min，并满足所有不等式约束:gi(x)≤0，i=1,2,3,…,n，所得x即优化设计方案x*。

然而，建立基坑稳定性和变形等与双排桩各结构参数之间精确关系式的数学模型是困难的。通过现场试验，用实测数值建立双排桩变形等与各结构参数之间的关系式是最可靠的，但无论费用还是工期，都要付出很高的代价，一般不具备这个条件。而专业设计软件提供了验算不同输入参数支护方案变形及稳定性的条件，使得建立响应曲面法关系成为可能。

1.2 响应曲面法

响应曲面法是通过试验数据，用回归方程拟合因素与响应值之间的函数关系，经对回归方程分析寻求最优工艺参数，解决多变量问题的一种统计方法。例如，欲求自变量x1和x2的水平以使得响应y达到最大值，y是x1和x2水平的函数，即

y=f(x1,x2)+ε

(1)

式中，ε代表响应y的观察误差或噪声。如果记期望响应为E(y)=f(x1,x2)=η，则由η=f(x1,x2)表示的曲面叫作响应曲面(图1)[18]。

图1 响应η作为自变量x1和x2函数的响应曲面

一般情况下，响应和自变量之间的关系形式是未知的。如果响应适合于用自变量的线性函数建模，则可用一阶模型

y=β0+β1x1+β2x2+…+βkxk+ε

(2)

或用更高阶的多项式表示。

依据响应曲面法建立的统计模型如果满足检验条件，通过该数学模型求得最优解，可找到能得到最接近目标的响应时的设计变量组合。

1.3 均匀设计

出于成本的考虑，对建筑结构进行多种组合的试验通过检测数值进行建模往往是不现实的，但通过设计软件进行模拟试验会得到比较满意的结果。常用的试验设计是正交试验，但正交试验存在试验次数过多的问题。因此，这里采用均匀设计。其性质和正交表有很大不同，最大特点是因素较多时所需试验次数少[19]。

根据均匀设计得到的试验结果不能直观分析，需要用回归方法对其进行统计分析。

1.4 响应曲面优化模型

根据得到的数据，一般先用多元线性回归，如果不能通过检验或效果不好再用多项式回归。回归分析中应对模型中的因素进行回归显著性检验。只有通过显著性检验的回归方程才可用来预测[20]。

一个较好的回归模型要求显著水平的值小，而且决定系数要大[21]。如果线性回归方程经检验显著水平的值小，相关性不高，一般采用二次多项式回归。

1.5 优化求解

对于一些简单的问题可以通过试验数据或回归模型直接分析，但对于较复杂的问题，则必须借助优化求解方法得到参数的最优组合。

在优化设计中，将设计评价的标准作为目标函数，不同取值的量作为设计变量，应遵守的条件作为约束条件[22]，用优化方法即可求得最优解。

如果约束条件不能包含所有的现场条件，最终的结果需要根据实际情况适当调整。

2 应用实例

2.1 工程概况

拟建工程场地位于济南市南部。拟建2#楼长×宽为55 m×14.0 m，层高53.1 m，地上18层，地下3层，基底标高72.80 m。该楼及北侧车库作为一个基坑一起支护开挖。基坑支护周长约246 m，开挖深度为9.60～12.10 m。

基坑东侧南部为军职老干部临时使用道路，自南向北，东侧北部路东8 m为8#住宅楼，高18层，桩基础，1层地下室。北侧东部为正常使用道路，距基坑24 m北为9#住宅楼，高17层，桩基础，1层地下室。距8#住宅楼5.3 m范围内有地下管线分布。

由于紧靠住宅楼且有地下管线分布，对支护结构变形需按一级基坑变形控制设计，根据场地条件及规范规定[23]合同要求最大水平位移不超过30 mm。

与基坑支护有关的地层及支护设计参数见表1。

地下水埋藏较深，基坑开挖不考虑地下水影响。

表1 基坑支护设计参数

2.2 敏感性分析

土体性质对双排桩稳定性及变形影响是显著的[11]，但该场地地层条件较好，不考虑土体加固，故认为土体性质不变。混凝土强度等级等对基坑稳定性及变形也不敏感[16]，双排桩连梁尺寸直接与桩径关联[24]，即桩径确定了，连梁尺寸也随即确定，也不考虑。双排桩支护结构的敏感性分析仅考虑嵌固深度、桩径、桩距、排距等对基坑稳定性及变形的影响。

在固定其他因素的条件下，改变某一因素进行计算，得到双排桩支护结构影响的敏感性分析结果如图2所示。其中，地表沉降采用抛物线法的数值。

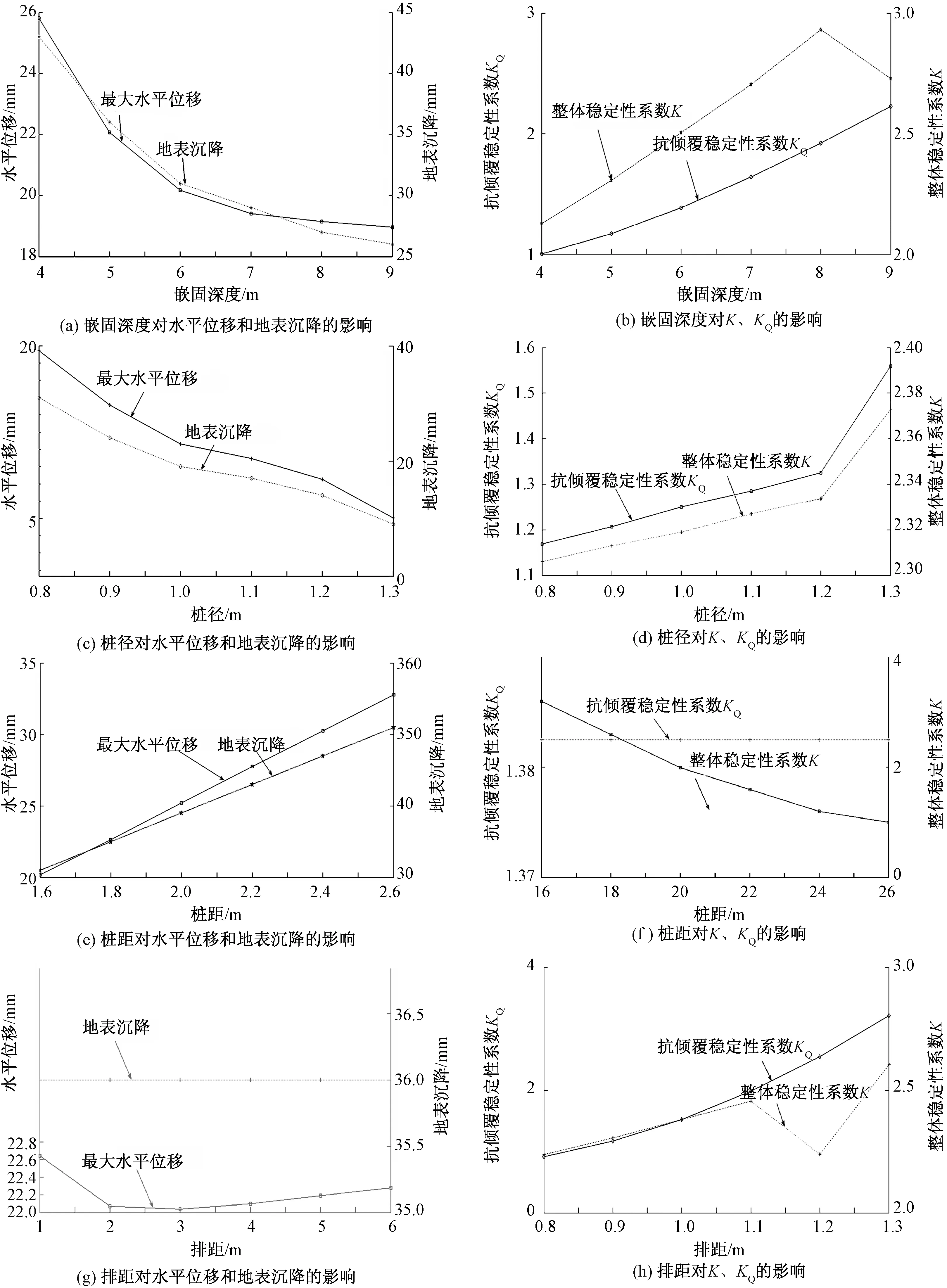
图2 基坑变形及稳定性与影响因素关系曲线

从图2看出，双排桩的嵌固深度对基坑变形及稳定性均有显著影响；桩径对基坑变形有显著影响，但对基坑稳定性影响不大；桩距对基坑变形也有显著影响，但对基坑稳定性影响不显著；双排桩的排距对基坑变形影响不显著，但对基坑稳定性影响显著。这些分析与文献[11]的结论基本一致。

2.3 确定试验因素和水平

通过以上敏感性分析，首先应考虑基坑的稳定性。其次，作为一级基坑，控制基坑最大水平位移，保证周边环境安全。为此，用桩嵌固深度、桩径、桩距和排距作为影响因素，选择8个试验水平安排模拟计算，设计参数水平见表2。

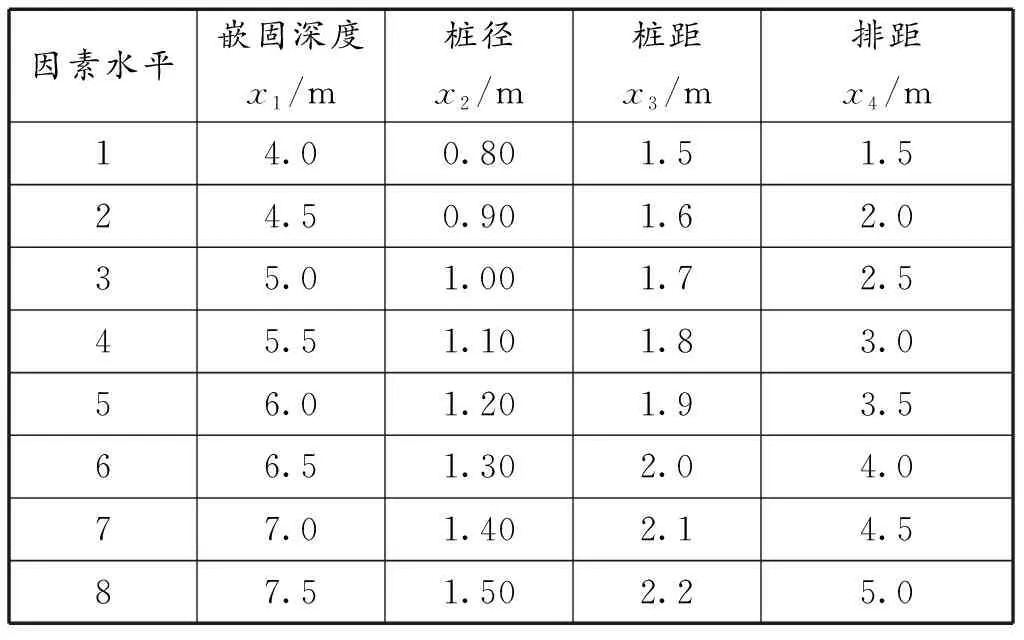
表2 设计参数水平

2.4 选择均匀设计表

由于因素水平有8个，故选择U*8(85)表(表3)。从U*8(85)的使用表(表4)看出，用4个因素的D为0.270 9，比U9(95) 表用4个因素的D(=0.406 6)[15]低很多，故选用U*8(85)表安排计算。

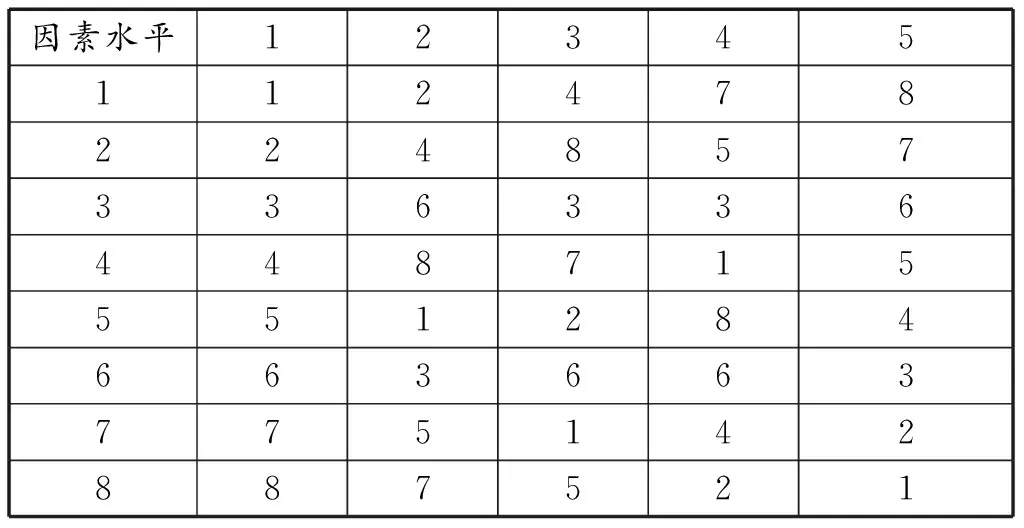
表3 均匀设计表U*8(85)

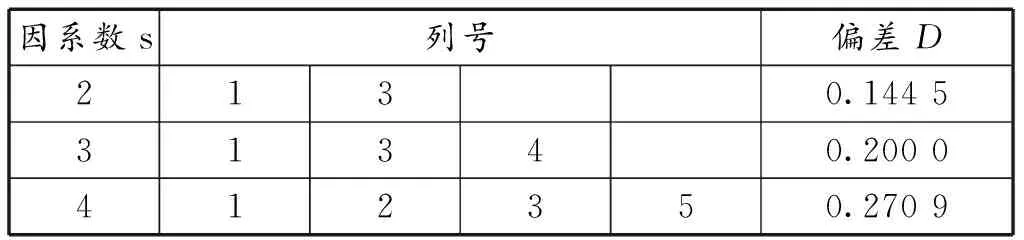
表4 U*8(85)的使用表

2.5 双排桩支护结构均匀设计数值模拟

按不同的结构参数组合，每一次验算为一次方案试验，共8个支护方案。

为减少优化目标个数，只选择最大水平位移和抗倾覆稳定性系数这两个最重要的指标进行求解，得到结果后再用专业设计软件验算基坑沉降和整体稳定性。用理正深基坑支护结构设计软件，计算结果见表5。

2.6 双排桩支护结构均匀设计数值模拟结果回归分析

采用DPS统计软件[21]对表5数据进行回归。由于试验次数8次不满足估计回归参数的必要条件[15]，因此采用逐步回归得

y=67.696 7-0.831 1x1-53.638 9x2+3.833 3x3

(3)

相关检验见表6(部分)。

从表6可知，相关系数R=0.958 7，F值的显著水平P值=0.011 9<0.05，决定系数=0.919 2较大,可用于预测。剔除双排桩排距后的回归方程与敏感性分析的结果相吻合。

对于抗倾覆稳定性，由于相关系数R=0.908 1，F值的显著水平P值=0.054 2>0.05，决定系数=0.824 6,故采用二次多项式回归方程得

(4)

相关检验见表7(部分)。

从表7可知，这个模型没有桩距(x3)，与敏感性分析结果是一致的，F值的显著水平P值=0.000 1<0.05，决定系数=0.997 8很大,故该模型可用于预测。

表5 最大水平位移、抗倾覆稳定性系数

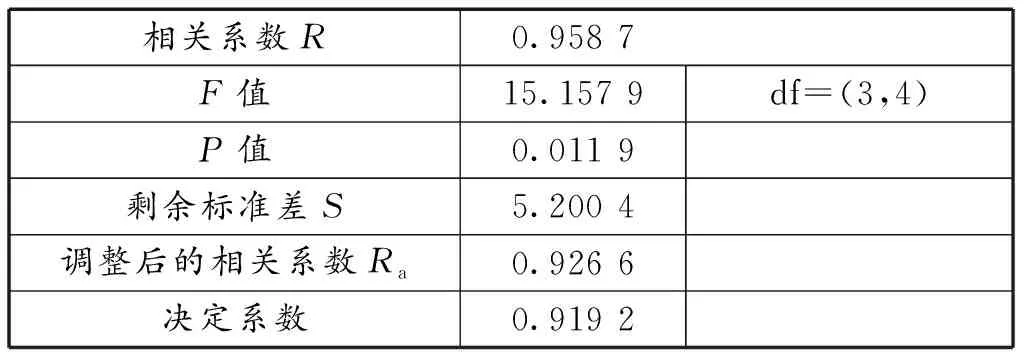
表6 多元线性回归检验

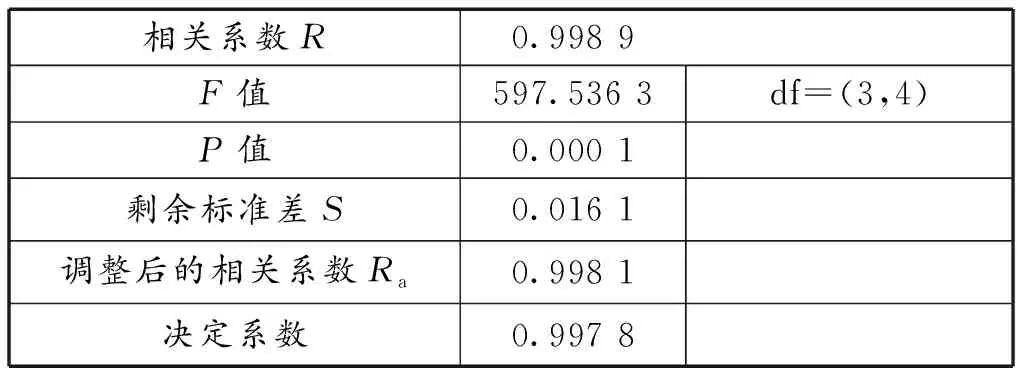
表7 二次多项式回归检验

2.7 双排桩支护结构优化设计

在满足约束条件下，可以对式(3)、式(4)进行优化求解，得到x1、x2、x3、x4的最优值。约束条件为

4.0≤x1≤6.0

(5)

0.8≤x2≤1.2

(6)

1.6≤x3≤2.0

(7)

1.0≤x4≤2.0

(8)

规定这些约束条件的依据是：

1)桩端进入强风化石灰岩，实际岩石强度比计算取值要高，现场不允许化学爆破，人工挖孔桩入岩施工难度极大，在计算满足稳定性的前提下尽可能小。

2)规范规定，人工挖孔桩最小直径为0.8 m，但随桩径增大，混凝土体积以二次方关系增加，开发商要求桩径控制在1.2 m以内。

3)人工挖孔桩要求护壁措施，即使跳挖方式施工，也应留有一定距离，故桩径0.8 m时取2倍径，即1.6 m桩距，桩径1.2 m适当小些，取2.0 m桩距。

4)基坑北侧东部为正常使用道路施工期间仅限2.0 m宽度，前后桩排距不能超过这个宽度。

对于最大水平位移，在约束条件(5)、(6)、(7)下，应用MATLAB2014a优化工具箱[25]求解式(3)得最大水平位移的最优组合参数x1=4.0，x2=0.8，x3=2.0，y=29.12。

由计算参数值可知，经8次迭代，利用内点方法，运算终止，不等式约束条件有效，但优化结果不收敛于解。事实上，经计算，嵌固4.0 m不满足抗倾覆稳定性要求，故将嵌固深度调整为6.0 m，计算抗倾覆稳定性系数KQ>1.25，满足规范规定要求。

由式(4)可知，在x1、x2已确定的条件下，将其代入式(4)即可方便地求得x4=1.6，无须再用优化工具箱求解。

因适当增加桩排距不会增加施工难度且仅需少量材料，考虑东侧道路条件，将桩排距x4由1.6 m调整为2.0 m，即采用x1=6.0，x3=0.8，x3=2.0，x4=2.0计算(图3)得：最大水平位移=22.39 m，地表沉降(抛物线法)=33 mm，KQ=1.381≥1.25,Ks=2.504≥1.35, 满足规范要求。

由于施工质量控制严格，加之桩端基本进入强风化灰岩，连梁与冠梁混凝土整体浇筑，基坑使用过程中实际监测深层水平位移未超过20 mm，达到预期的目标。

图3 最终计算模型

根据现场实际，对照规范分析，东侧仅4 m宽空间，且要求不能中断人行通道，尽管前后支护桩排距的增大可以明显提高基坑的抗倾覆稳定性，但限于场地条件，最大也只能采用2.0 m排距，满足规范2d～5d(d为桩径)的要求。而人工挖孔桩采用0.8 m的直径是一个最小的尺寸。与规范要求相比，2.0 m的桩距显略大，但人工挖孔桩护壁厚度150 mm，实际孔径1.1 m，过小的桩距容易出现串孔。嵌固深度比规范规定[0.6h(h为基坑深)]小，但中风化灰岩抗剪强度高，验算满足稳定性要求。

基坑开挖后现场如图4(中间部位)所示。该单元原设计双排桩嵌固深度7.5 m、桩径0.9 m、桩距1.8 m，优化后桩数减少，桩长缩短，节省钢筋混凝土用量31.8%。

图4 基坑开挖后现场

3 结论

双排桩支护结构优化的难点之一是目标函数的构建。通过专业软件计算双排桩支护结构变形，建立变形与设计参数的回归方程，即基坑稳定性及变形的响应曲面关系，以回归方程作为目标函数进行优化求解是本文的创新之一。结合实例设计计算，得到以下结论：

1)双排桩嵌固深度、桩径、桩距、前后桩排距是影响稳定性及变形最主要的因素，采用响应曲面法能够快速方便地得到最优的支护方案。

2)应用理正深基坑支护设计软件，建立基坑稳定性及变形的响应曲面关系，是一种方便、实用的结构优化设计方法。

3)基于响应曲面法的双排桩支护结构优化设计是结构设计方法的发展，但它本质上也还是一个工具而已，它不可能解决力学理论和设计思想所未解决的问题，更不能代替人的思维，必须结合现场实际，通过概念设计确定最终方案。