农田输水隧洞内力计算分析

张敬博，张文强，刘 辉

(1.杨凌职业技术学院，陕西 杨凌712100； 2.济宁市规划设计研究院，山东 济宁272000；3.昆明市官渡区水务局，云南 昆明650031)

0 引言

当前世界各国都开展了各种大型的水利工程建设，我国的水利行业也在蓬勃发展[1]。水利行业的发展是农业可持续发展的关键，农业水利工程的发展在很大程度上影响水利行业的整体发展[2]。随着农业水利工程的快速发展，农田输水隧洞的建设规模越来越大，建设条件也日趋复杂，隧洞结构设计理论和方法也随之快速发展。以新奥法为基础进行设计和施工的隧洞复合衬砌结构就是一种新型支护结构，相对于传统隧洞支护理论，复合衬砌结构理论认为围岩和衬砌联合承载，围岩既是产生围岩压力的主体，又是承担这一压力的结构主体。但是对于隧洞复合衬砌结构中初次支护与二次衬砌联合承载时的荷载分担问题，并没有一个明确的认识。目前国内外对隧洞复合式衬砌结构设计大多是通过工程类比结合一定的结构计算分析综合确定[3]。孙振宇等[4]对3种不同协同作用的复合支护结构进行解析，得出基于支护承载能力曲线的隧道复合支护结构安全评价方法。曹生荣等[5]以南水北调穿黄隧洞为工程背景，分析垫层预应力复合衬砌的盾构输水隧洞受力特点。梁娟等[6]对猴子岩水电站导流隧洞进行结构分析，得出洞身采用复合式衬砌，既能满足施工期的安全，又能满足导流洞正常运行且安全可靠的结论。谢小玲等[7]通过对穿黄隧洞衬砌进行模型仿真试验，研究分析无垫层衬砌段、有垫层衬砌段两种不同结构的受力特性。杨光华等[8]对盾构隧洞复合衬砌在高内水压力的情况下采用荷载结构法，分别计算围岩、各层衬砌结构单独承担内水压力时径向位移与内水压力关系，确定出复合衬砌各自分担的内水压力。

对于隧洞结构设计，SL279—2016《水工隧洞设计规范》中明确规定：当围岩条件较差，衬砌需要的厚度过大时，可采用外层为混凝土或钢筋混凝土、内层为锚喷支护的组合式双层衬砌，即复合衬砌[9]。由于复合衬砌受力状态复杂，结构形式特殊，因此在设计时可认为初期支护仅起到施工阶段临时支护的作用，由二次衬砌承受全部荷载；也可认为荷载将由初期支护和二次衬砌以一定比例共同承担。无论是初次支护还是二次衬砌，其承担的荷载大小都与其刚度成正比，但过分增大初期支护或二次衬砌的刚度也是不经济的[3]。因此，在进行复合衬砌结构设计时，需要根据工程实际情况，提出既能满足结构安全性要求又能兼顾经济性要求的设计。

基于前人的研究经验，本文以云南临沧市某无压输水隧洞为例，参考JTG D70—2004《公路隧道设计规范》，采用结构力学方法，按照初期支护和二次衬砌以7∶3的荷载分担比例进行复合衬砌结构内力计算，通过分析研究结构设计成果并从中得到一些有用结论，以期对同类型的输水隧洞设计施工具有一定的指导意义和参考价值[10]。

1 工程简况

研究对象为城门洞型无压隧洞，洞段总长3 089 m，隧洞底坡1∶500。根据不同隧洞沿线的水文及工程地质情况，将隧洞分段采用不同的衬砌形式。开挖段地质描述：隧洞所处地带岩性基本为层状砂岩夹硅质砂岩、砂砾岩；其风化严重，受地质构造影响，节理、裂隙发育，地下水活动频繁，时常洞壁及顶拱潮湿、渗水、滴水等；开挖时，常见顶拱及边墙塌落、掉块等地质超挖现象，隧洞沿线总体上属于Ⅳ～Ⅴ类不稳定岩体，也有部分洞段为Ⅰ～Ⅲ类围岩。

隧洞支护参数一般采用工程类比法进行确定。对于Ⅰ～Ⅲ类围岩，由于岩体自身稳定性好，具有很高的承载能力，故不再进行结构计算分析；而对于Ⅳ～Ⅴ类不稳定岩体则应该在工程类比的基础上开展结构验算工作。

本文仅就工程中Ⅳ类围岩条件下隧洞进行洞身断面复合衬砌结构设计，并根据荷载-结构法对二次衬砌进行结构运算，并验算其稳定性。

2 隧洞复合衬砌设计

隧洞断面设计为城门洞型无压隧洞，经过水利计算，确定隧洞断面尺寸为高3 200 mm、宽3 600 mm、拱高1 800 mm。依据隧洞沿线不同水文及工程地质条件，拟将隧洞分段采用不同的衬砌形式。对于Ⅳ类围岩隧洞段，根据工程经验拟定初次支护采0.2 m厚C20混凝土喷锚支护，锚杆为Φ25锚杆，沿隧洞拱圈均布；二次衬砌采用0.3 m厚C20钢筋混凝土支护。其中，二次衬砌C20钢筋混凝土的配筋情况根据结构计算确定。Ⅳ类围岩隧洞衬砌结构如图1所示。具体指标如表1所示。

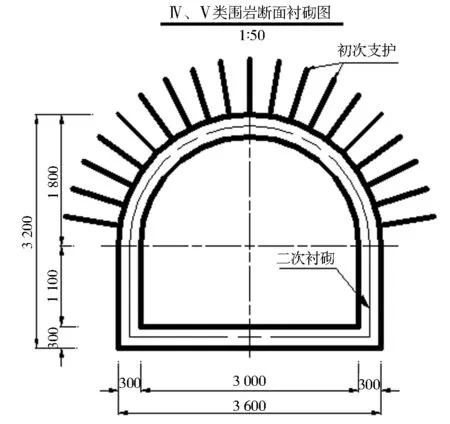
图1 Ⅳ类围岩隧洞衬砌结构

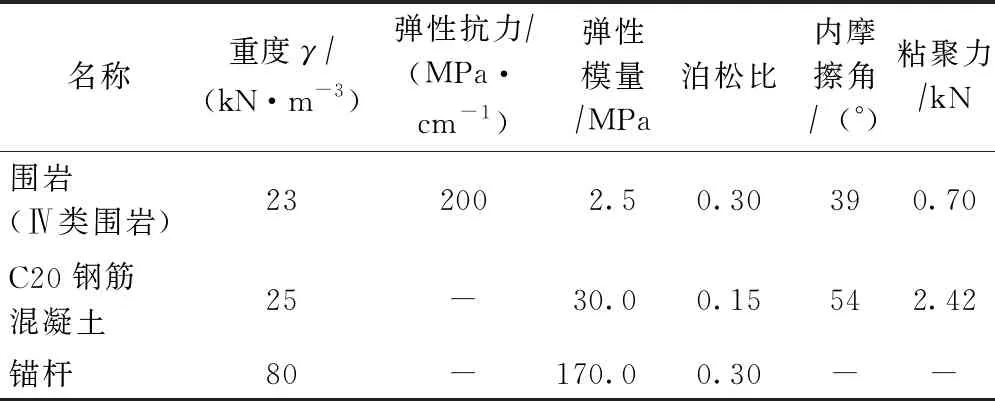
表1 围岩及衬砌材料物理力学指标

3 二次衬砌结构内力计算

3.1 围岩压力计算

围岩压力为隧洞开挖后围岩变形或塌落作用在支护上的压力。目前，确定围岩压力的方法有松散介质理论(普氏理论)、围岩压力系数法(水利规范建议计算法)和弹塑性理论法等，本文分别采用松散介质理论和围岩压力系数法计算围岩压力，结构计算取其中大值。围岩压力计算成果如表2所示。

表2 隧洞围岩压力计算结果

3.2 外水压力计算

外水压力是地下水头引起的，规范规定外水压力是作用在衬砌外表面的边界力。外水压力对无压隧洞通常起控制作用，而对有压隧洞则有对内水压力抵消的作用[11]。由于影响地下渗流的因素较多，因此，外水压力的值通常无法准确确定。常用的方法是将地下水面以上的水柱高乘以折减系数β作为外水压力值。该方法简单方便，在工程上一直广泛应用(虽然近似粗略)。外水压力计算结果如表3所示。

表3 隧洞外水压力计算结果

3.3 隧洞衬砌自重计算

衬砌自重是指沿隧洞轴线1 m长的衬砌自重，均匀作用于衬砌厚度的平均线上。单位面积上的自重强度g为

g=γc·h

(1)

式中γc—衬砌材料的容重

h—包括超挖在内的衬砌厚度

隧洞衬砌厚度为300 mm，衬砌材料(钢筋混凝土)容重为24 kN/m3，因此，隧洞衬砌自重为g=0.3 m×24 kN/m3=7.2 kN/m2。

3.4 其他荷载

作用于隧洞衬砌结构上的其他荷载还包括灌浆压力、地震力、温度荷载等。本次计算仅考虑围岩压力、水压力及隧洞衬砌自重这3种主要荷载，而不考虑灌浆压力、温度应力、地震荷载等作用。

4 内力计算结果及分析

根据上述方法，分别计算以下两种工况下的隧洞二次衬砌混凝土内力：第1种是考虑初期支护与二次衬砌结构共同承载且承载比例为7∶3工况；第2种是未考虑初期支护与二次衬砌联合承载，即外荷载完全由二次衬砌独自承担工况。两种工况下二次衬砌结构内力计算结果对比如表4所示。

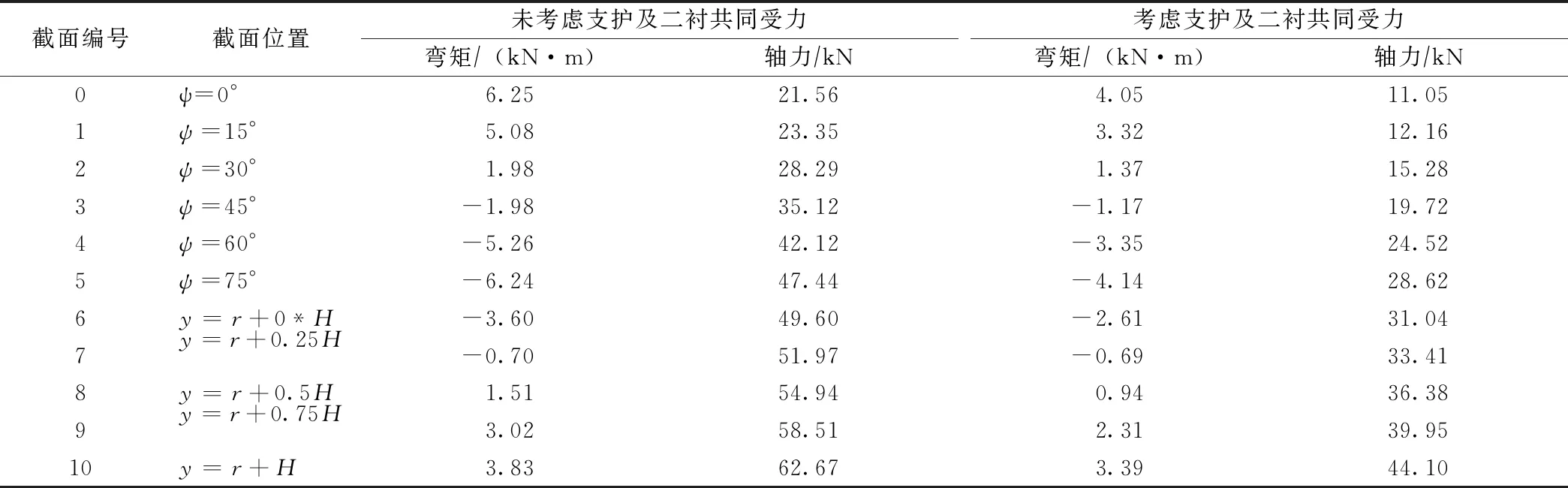
表4 隧洞各截面内力计算结果对比

根据隧洞各截面在未考虑初期支护与二次衬砌联合承载和考虑二者共同承载两种工况下的弯矩、轴力计算结果，绘制出弯矩及轴力图，如图2所示。

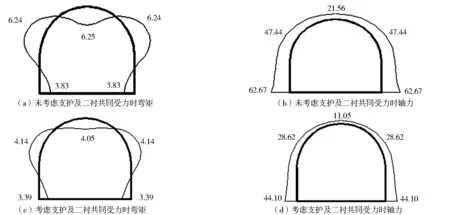
图2 Ⅳ类围岩内力图

根据表4结果，考虑支护及二衬共同受力及未考虑两者共同受力的轴力随截面的变化趋势如图4所示。

由表4、图3可以看出：当考虑初期支护与二次衬砌联合承载且承载比例为7∶3时，最大弯矩出现在拱顶处，最大轴力出现在直墙墙角处，弯矩最大值为4.05 kN·m，轴力最大值为44.10 kN；当不考虑二次衬砌与初期支护共同承载时，此时全部的外荷载由二次衬砌独自承担，属于危险工况，二次衬砌内力较大，最大弯矩同样发生在拱顶处、最大轴力也发生在直墙墙角处，弯矩最大值为6.25 kN·m，轴力最大值为62.67 kN。两种不同算法的弯矩值最大值差2.2 kN·m，考虑初期支护与二次衬砌联合承载比不考虑两者共同受力弯矩值减少35.20%。由轴力随截面的变化趋势可知，未考虑支护及二衬共同受力的轴力趋势线始终处于考虑支护及二衬共同受力的轴力趋势线上方，两条线基本处于平行状态。0号截面处未考虑支护及二衬共同受力的轴力为21.56 kN，考虑支护及二衬共同受力的轴力为11.05 kN，两种不同算法的差值为10.51 kN，轴力值减小约48.74%。5号截面处未考虑支护及二衬共同受力的轴力为47.44 kN，考虑支护及二衬共同受力的轴力为28.62 kN，两种不同算法的差值为18.82 kN，轴力值减小39.67%。10号截面处未考虑支护及二衬共同受力的轴力为62.67 kN，考虑支护及二衬共同受力的轴力为44.10 kN，两种不同算法的差值为18.57 kN，轴力值减小29.63%。对比上述两种工况下的二次衬砌结构内力，在考虑初期支护与二次衬砌联合承载工况下，最大弯矩值减小35.20%，最大轴力值减小约48.74%；两种工况下，弯矩与轴力都是对称分布的，这是由于隧洞计算模型及荷载的对称性。

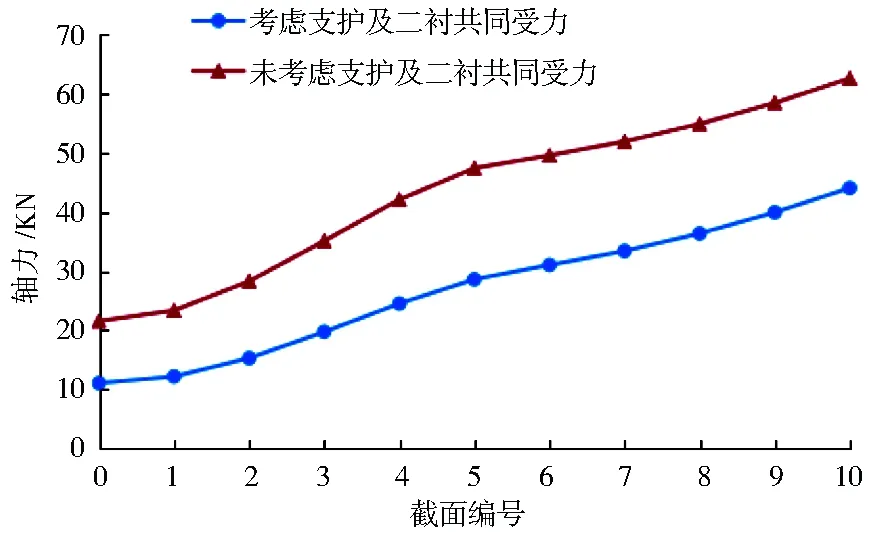
图3 轴力随截面变化趋势

为了保证隧洞结构安全性，取上述两种工况中最危险工况，即在进行应力验算时不考虑初期支护的承担荷载，此时所有外荷载都由二次衬砌承担[12]。不考虑初期支护与二次衬砌联合承载时弯矩、轴力计算成果，根据材料力学中的应力计算公式得出二衬混凝土的内、外侧拉应力及压应力，计算结果表明：最大拉应力为362 kN/m2，出现在拱顶处，远小于C20混凝土的允许拉应力937.65 kN/m2；最大压应力为615 kN/m2，出现在直墙墙顶附近，小于C20混凝土的允许压应力7 692.5 kN/m2。由此可知，使用30 cm厚的C20混凝土衬砌能够满足隧洞安全需求。

5 结论

(1)圆拱直墙隧洞的二次衬砌结构受力不均匀。其最大弯矩发生在拱顶处，最大轴力发生在直墙墙角处。其中，轴力呈半椭圆形分布，弯矩和轴力图都是对称的，这是由于计算模型和荷载分布都是对称的。

(2)对比分析考虑支护及二衬共同受力及未考虑两者共同受力两种工况，在考虑初期支护与二次衬砌联合承载工况下，最大弯矩值相比未考虑两者共同受力时减小35.20%，最大轴力值减小约48.74%。通过对衬砌最危险工况的验算，在进行无压隧洞复合衬砌结构设计时，考虑初次支护与二次衬砌联合承载并按照7：3的荷载承担比例进行结构设计计算是安全的，也更符合工程实际。