山西省农村居民收入的组合预测研究

太原工业学院理学系 连高社

前言

中国是一个农业大国，而山西省的农业并不十分发达，“三农” 问题一直都是中国关注的重点问题，就其本质上而言，“三农”问题的核心就是增收，提高农民的可支配收入。农村居民人均可支配收入的高低是评判农村经济发展快慢和农村居民生活水平是否提高的重要依据。因此本文的重点就是预测山西省农村居民人均可支配收入。

1 指数函数模型

人均可支配收入，是指平均每个人可以用来自由支配的收入，一般来说，可支配收入常常被用来衡量一个地区人们的生活水平，二者之间成正比，可支配收入越高，就意味着当地生活水平越高，因此采用农村人均可支配收入作为农村居民收入的指标进行研究。设初始数据变量为PCDI（人均可支配收入），用Eviews8.0 做出PCDI 的时序图，可以看到，人均可支配收入随着时间的推移快速增长，呈现出指数增长的形式，因此现在以PCDI作为因变量，时间t 作为自变量，构造人均可支配收入关于时间的指数函数模型[1]。

首先重新定义时间t 的取值范围为1~19 （对应原来的2000~2018 年），将因变量人均可支配收入PCDI 取自然对数得lnpcdi，先在Eviews8.0 软件中，采用最小二乘法拟合出lnpcdi 与t 的线性回归方程，最后再把线性回归方程进行还原，得到指数模型表达式。

由上述参数估计结果可知，给定显著性水平0.05，变量t 与常数项前系数对应的P 值均小于显著性水平，故拒绝原假设，认为变量系数均有效；模型的拟合优度R2=0.994665，表明模型拟合效果非常好。

将上述线性模型还原为指数模型，表达式为：

2 ARIMA 模型

ARIMA 模型是通过差分的方式把所要研究的时间序列模型转化为平稳的，然后再进行建模的，所以ARIMA（p，d，q）称为差分自回归移动平均模型，其中的d 就是在做平稳化处理时的差分次数。ARIMA 模型最后是检验残差的，可以很好地减小预测的误差，但是ARIMA 模型本身认为所要研究的时间序列从始至终的趋势是一致的，所以它在预测时，不能分析到有意外的发生[2]。

2.1 数据的平稳性处理和白噪声检验

从数据和PCDI 的时序图可以看出，变量PCDI 具有明显的上升趋势，因此可以基本认为变量PCDI 不是平稳时间序列，需要对变量PCDI 进行平稳化处理。对变量PCDI 直接进行一次差分，得到变量DPCDI，时序图如图1 所示。

图1 变量DPCDI 时序图

由图1 可知，变量DPCDI 不具有明显的趋势性与周期性，因此可初步认为变量DPCDI 具有一定的平稳性。

对变量PCDI、DLPCDI 进行ADF 检验，变量PCDI 存在单位根，变量PCDI 为非平稳时间序列。变量DPCDI 没有单位根，具有平稳性。变量DPCDI 是非白噪声的。

2.2 模型识别与参数估计

观察自相关图与偏自相关图，变量DPCDI 自滞后1 阶后快速落入随机区间内。为寻找合适的模型估计参数，采用穷举法，分别建立带有常数项的ARI(1,1)、ARI(2,1)以及ARIMA(1,1,1)等模型。

建模后，综合考虑AIC 准则与SIC 准则，并结合模型系数的有效性，最终选择ARI(1,1)模型作为最终的预测模型，ARI（1,1）模型的拟合优度为0.565901，表明模型拟合效果良好。具体的模型表达式与参数估计如公式3 所示：

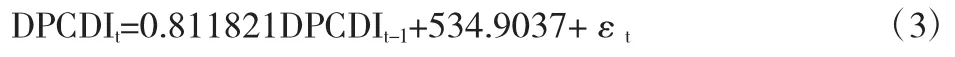
给定显著性水平为0.05，参数AR(1)与常数项系数对应的P值均小于显著性水平，说明模型系数显著不为0。

2.3 模型检验

对模型的残差进行白噪声检验，残差的各个Q 统计量所对应的P 值都远大于0.05，可以认为模型的残差是白噪声序列。所以认为AIR(1,1)模型是可以进行建模和预测的。

2.4 模型预测

利用ARI(1,1)模型使用Eviews 进行预测，对2000~2018 年数据采用静态预测法拟合，对2019~2023 年的数据采用动态预测法预测。

3 灰色预测模型

著名学者邓聚龙教授创建了灰色系统理论[3]，灰色模型在数据的处理和对未来趋势的预测等方面都很有独到性。

通过Matlab 计算得到如下结果：a（发展系数)=-0.1022，b（灰作用量）=1896.44143535264。

所以模型表达式为

此外，用MATLAB 代码求出的Q=0.0541，C=0.0969，P=1，用求出的三个指标对照精度表，进行精度对比，可得：

从表1 可以看出，相对误差Q 合格，均方差比值C 和小概率误差P 均是好，说明该模型拟合较好，可以进行建模和预测。

表1 灰色模型检验指标精度表

4 组合预测模型

组合预测的思想就是依据一个标准建立一个函数，然后通过已知的信息求出这个函数在区间内的极值，这样就可以得到每一种预测模型的权重系数，就得到了最优的组合预测模型[4]。

将第t 期实际值、预测值分别记为y1、fit，则预测的误差为：

求解条件极值：

其中，Wn=(W1,W2,...,Wn)是组合权重向量，En=(Cij)n×n是预测误差信息矩阵，

对于本文所要研究的3 种单项预测模型，设f1为指数函数模型，f2为灰色GM(1,1)预测模型，f3为ARMA 预测模型。那么可以通过Excel 求出这三种单项预测模型的信息误差矩阵为：

用MATLAB 编程计算，可得到组合预测模型预测权重向量为：w=(-0.024252428 0.279343498 0.74490893)T，所以建立的组合预测模型表达式为：

5 模型效果评价与预测

从表2 可以看出，组合预测模型的各种误差指标都小于其他的单项预测模型，因此可以认为组合预测模型的误差更小，预测更准确，可以用组合预测模型来进行预测，现在利用该模型对山西省农村居民2019~2023 年的可支配收入进行预测，预测结果如表3 所示：

表2 四种模型预测效果评价指标比较

表3 四种模型对2019~2023 年的预测值

最终预测出2019~2023 年的山西省农村居民人均可支配收入分别为：10750 元，11521 元，12334 元，13193 元，14103 元，每年的增长率分别为：7.17%，7.06%，6.96%，6.90%，可以看出山西省农村居民人均可支配收入每年都在稳定增长，而且增长率较平稳。